青岛版 七下 8.2角的比较同步课时训练(word版含答案)
文档属性
| 名称 | 青岛版 七下 8.2角的比较同步课时训练(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 456.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 00:00:00 | ||
图片预览



文档简介
8.2角的比较同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
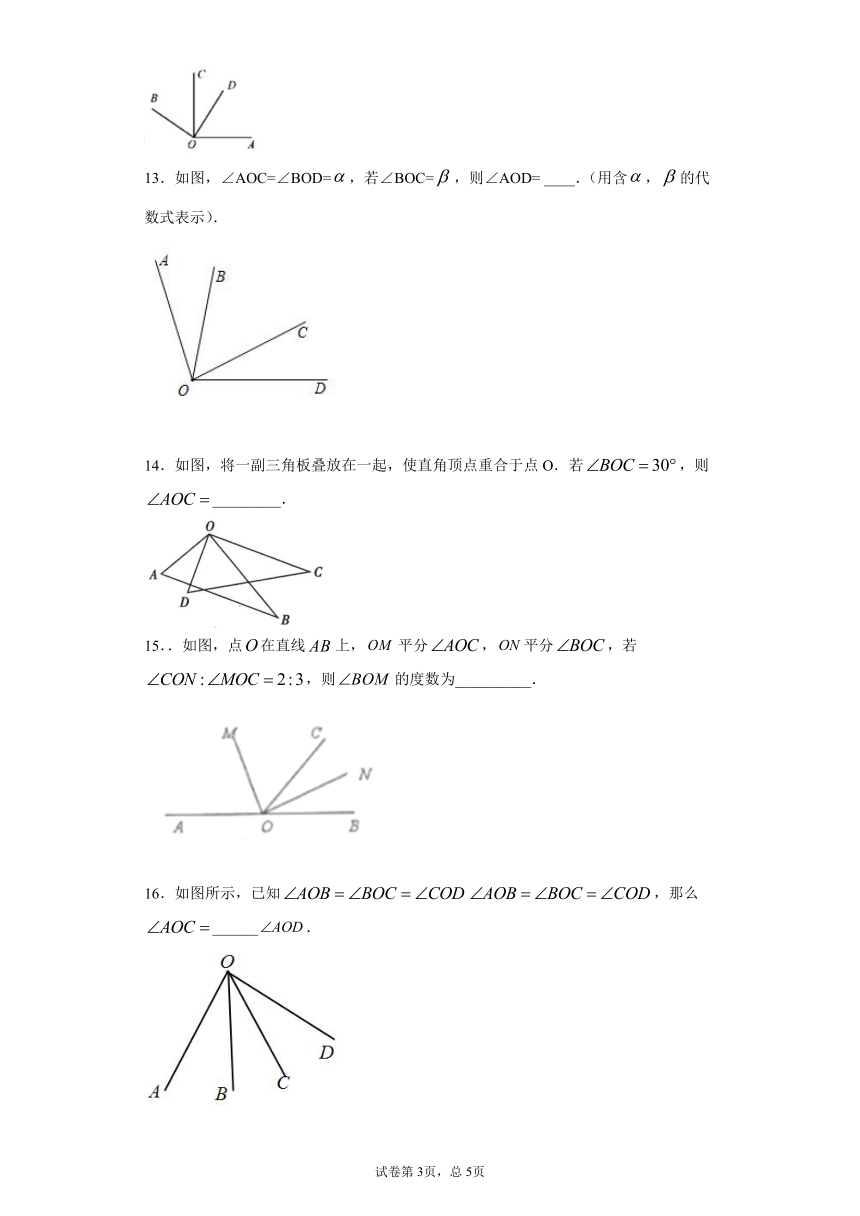
1.在时刻9:30,墙上挂钟的时针与分针之间的夹角是( )
A.115° B.105° C.100° D.90°
2.如图,OC是的平分线,OD是的平分线,且,则等于( )
A. B. C. D.
3.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.105° B.95° C.85° D.75°
4.有如下说法:①直线是一个平角;②如果线段,则是线段的中点;③在同一平面内,,,;④两点之间,线段最短.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.如图,OC为内的一条射线,下列条件中不能确定OC平分的是( )
A. B.
C. D.
6.和的顶点和一边都重合,另一边都在公共边的同侧,且,那么的另一半落在的( )
A.另一边上 B.内部; C.外部 D.以上结论都不对
7.用一个放大10倍的放大镜看一个10°的角,这个角是( )
A.100° B.10°
C.110° D.170°
8.如图所示,点A、O、E在一条直线上,,那么下列各式中错误的是( )
A. B.
C. D.
9.若∠1=,∠2=78.6°,∠3=,则有( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.以上都不对
10.邮轮在航行中,发现灯塔在它南偏东的方向上,同时在它北偏东方向上又发现了货轮,且客轮正好在的平分线上,那么客轮在邮轮的( )
A.正东方向上 B.正西方向上 C.北偏东方向上 D.北偏西方向上
二、填空题
11.已知OC是∠AOB的平分线,∠BOD=?∠COD,OE平分∠COD,设∠AOB=β,则∠BOE=_____.(用含β的代数式表示)
12.如图,已知,,则等于__________.
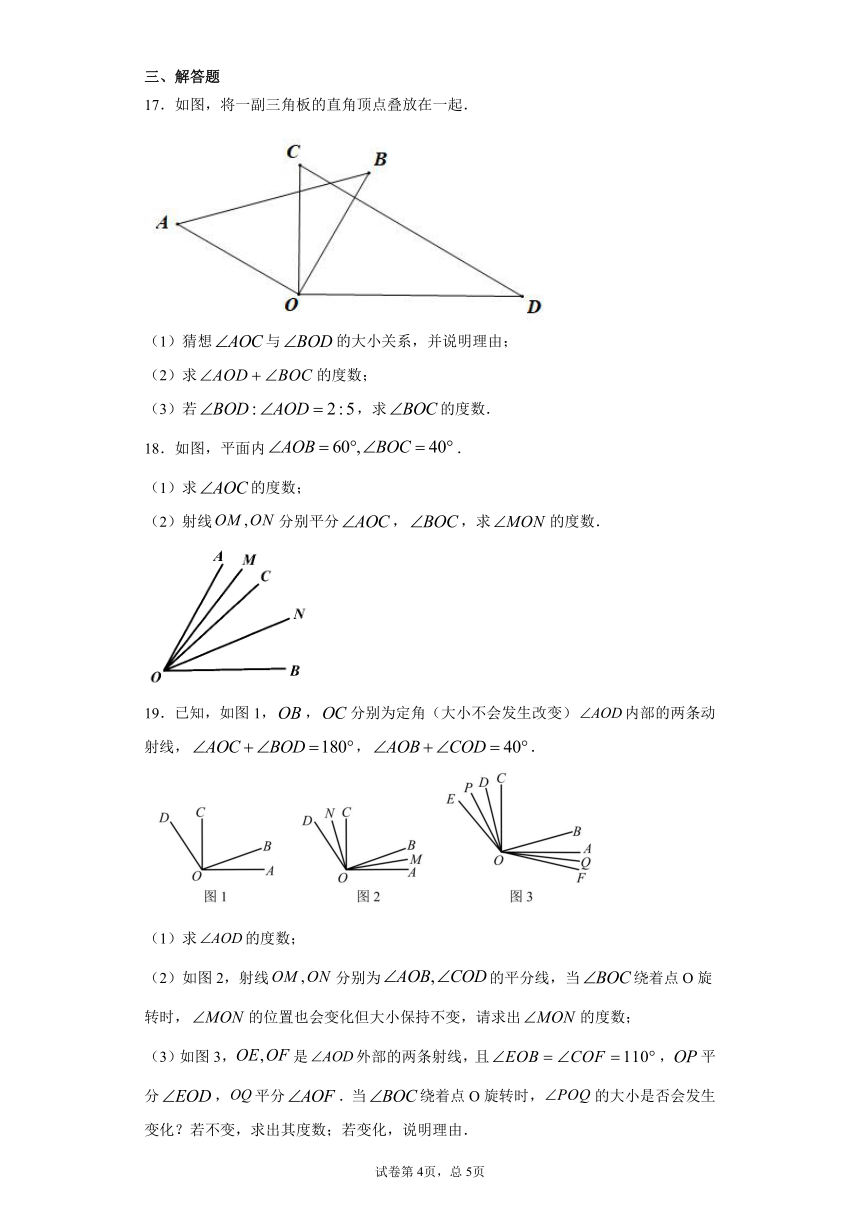
13.如图,∠AOC=∠BOD=,若∠BOC=,则∠AOD= ____.(用含,的代数式表示).
14.如图,将一副三角板叠放在一起,使直角顶点重合于点O.若,则_________.
15..如图,点在直线上,平分,平分,若,则的度数为__________.
16.如图所示,已知,那么______.
三、解答题
17.如图,将一副三角板的直角顶点叠放在一起.
(1)猜想与的大小关系,并说明理由;
(2)求的度数;
(3)若,求的度数.
18.如图,平面内.
(1)求的度数;
(2)射线分别平分,,求的度数.
19.已知,如图1,,分别为定角(大小不会发生改变)内部的两条动射线,,.
(1)求的度数;
(2)如图2,射线分别为的平分线,当绕着点O旋转时,的位置也会变化但大小保持不变,请求出的度数;
(3)如图3,是外部的两条射线,且,平分,平分.当绕着点O旋转时,的大小是否会发生变化?若不变,求出其度数;若变化,说明理由.
20.如图,是直线上一点,以为顶点作,且,位于直线两侧,平分.
(1)当时,求的度数;
(2)通过(1)的计算,请你猜想和的数量关系,并说明理由.
参考答案
1.B
2.D
3.C
4.A
5.B
6.C
7.B
8.C
9.B
10.C
11.β或β
12.30°
13.
14.
15.
16.
17.(1),理由见解析;(2);(3).
【详解】
解:(1),
理由是:∵,
∴,
∴;
(2)∵,
∴
;
(3)∵,
∴设,则
∵,
∴
∴
∴
∴
∴.
18.(1)20°;(2)30°
【详解】
解:(1)
(2) 分别平分,,
19.(1);(2);(3)的大小不变为.
【详解】
解:(1)∵,
∴
∵,
∴
∴
(2)∵射线,分别为,的平分线,
∴,
∴
∴
∴的度数为.
(3)的大小不变为.理由如下:
∵,,
∴,
,
∵
∴
∵平分,平分
∴
∴
20.(1)100°;(2),理由见解析.
【详解】
解:(1)∵,,
∴,
∵平分,
∴,
∴;
(2),理由如下:
∵,
∴,
∵平分,
∴,
∴.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在时刻9:30,墙上挂钟的时针与分针之间的夹角是( )
A.115° B.105° C.100° D.90°
2.如图,OC是的平分线,OD是的平分线,且,则等于( )
A. B. C. D.
3.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.105° B.95° C.85° D.75°
4.有如下说法:①直线是一个平角;②如果线段,则是线段的中点;③在同一平面内,,,;④两点之间,线段最短.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.如图,OC为内的一条射线,下列条件中不能确定OC平分的是( )
A. B.
C. D.
6.和的顶点和一边都重合,另一边都在公共边的同侧,且,那么的另一半落在的( )
A.另一边上 B.内部; C.外部 D.以上结论都不对
7.用一个放大10倍的放大镜看一个10°的角,这个角是( )
A.100° B.10°
C.110° D.170°
8.如图所示,点A、O、E在一条直线上,,那么下列各式中错误的是( )
A. B.
C. D.
9.若∠1=,∠2=78.6°,∠3=,则有( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.以上都不对
10.邮轮在航行中,发现灯塔在它南偏东的方向上,同时在它北偏东方向上又发现了货轮,且客轮正好在的平分线上,那么客轮在邮轮的( )
A.正东方向上 B.正西方向上 C.北偏东方向上 D.北偏西方向上
二、填空题
11.已知OC是∠AOB的平分线,∠BOD=?∠COD,OE平分∠COD,设∠AOB=β,则∠BOE=_____.(用含β的代数式表示)
12.如图,已知,,则等于__________.
13.如图,∠AOC=∠BOD=,若∠BOC=,则∠AOD= ____.(用含,的代数式表示).
14.如图,将一副三角板叠放在一起,使直角顶点重合于点O.若,则_________.
15..如图,点在直线上,平分,平分,若,则的度数为__________.
16.如图所示,已知,那么______.
三、解答题
17.如图,将一副三角板的直角顶点叠放在一起.
(1)猜想与的大小关系,并说明理由;
(2)求的度数;
(3)若,求的度数.
18.如图,平面内.
(1)求的度数;
(2)射线分别平分,,求的度数.
19.已知,如图1,,分别为定角(大小不会发生改变)内部的两条动射线,,.
(1)求的度数;
(2)如图2,射线分别为的平分线,当绕着点O旋转时,的位置也会变化但大小保持不变,请求出的度数;
(3)如图3,是外部的两条射线,且,平分,平分.当绕着点O旋转时,的大小是否会发生变化?若不变,求出其度数;若变化,说明理由.
20.如图,是直线上一点,以为顶点作,且,位于直线两侧,平分.
(1)当时,求的度数;
(2)通过(1)的计算,请你猜想和的数量关系,并说明理由.
参考答案
1.B
2.D
3.C
4.A
5.B
6.C
7.B
8.C
9.B
10.C
11.β或β
12.30°
13.
14.
15.
16.
17.(1),理由见解析;(2);(3).
【详解】
解:(1),
理由是:∵,
∴,
∴;
(2)∵,
∴
;
(3)∵,
∴设,则
∵,
∴
∴
∴
∴
∴.
18.(1)20°;(2)30°
【详解】
解:(1)
(2) 分别平分,,
19.(1);(2);(3)的大小不变为.
【详解】
解:(1)∵,
∴
∵,
∴
∴
(2)∵射线,分别为,的平分线,
∴,
∴
∴
∴的度数为.
(3)的大小不变为.理由如下:
∵,,
∴,
,
∵
∴
∵平分,平分
∴
∴
20.(1)100°;(2),理由见解析.
【详解】
解:(1)∵,,
∴,
∵平分,
∴,
∴;
(2),理由如下:
∵,
∴,
∵平分,
∴,
∴.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
