青岛版 七下 8.3角的度量同步课时训练(word版含答案)
文档属性
| 名称 | 青岛版 七下 8.3角的度量同步课时训练(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 381.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 17:19:56 | ||
图片预览




文档简介
8.3角的度量同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,∠AOB=∠COD=90°,若∠BOD=150°,则∠BOC的度数为( )
A.150° B.120° C.90° D.60°
2.若与互补(),则与的关系是( )
A.互补 B.互余 C.和为 D.和为
3.如图,三角板中是直角,的顶点在直尺的边上,下面结论错误的是( )
A.与互余 B.
C. D.
4.已知∠1=39°15′,则∠1的余角为( ).
A.50°45′ B.50°85′ C.60°45′ D.60°85′
5.下列说法①互为相反数的两个数的同一偶数次方相等; ②与是同类项;③若关于x的方程的解是-2,则a的值是0;④一个角的补角一定大于这个角.其中正确的结论有几个?( )
A.1 B.2 C.3 D.4
6.已知:∠,∠,∠,则下列说法正确的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.∠1、∠2、∠3互不相等
7.如图,,,则的度数为( )
A. B. C. D.
8.如图,,在下面的四个式子中:①;② ;③;④,可以表示为 的补角的式子的个数是( )
A.1 B.2 C.3 D.4
9.如图,,以为一边作,则的度数为( )
A. B. C.或 D.或
10.如图,若,则下列结论一定正确的是( )
A. B.
C. D.
二、填空题
11.一副三角板如图摆放,若,则的度数是__________.
12.已知的余角是,则为________°.
13.如图,某市有三个中学A,B,O.中学A在中学O的北偏东61°15′的方向上,中学B在中学O的南偏东39°45′的方向上,则∠AOB的度数是_____.
14.如图,在直角∠AOB的内部作射线OC,若∠AOC=33°24′17″,则∠BOC=_____.
15.一副三角板如图放置(直角顶点叠放在一起),若,则______度.
16.如图,某一时刻在灯塔O处观测到游轮A在它的北偏西30°方向,同时又观测到货轮B在它的北偏东45°方向,则∠AOB的度数是_____°.
三、解答题
17.如图,直线与相交于点,,分别是,的平分线.
(1)写出的补角;
(2)若,求和的度数;
(3)射线与之间的夹角等于多少度?请说明理由.
18.已知点A,B,O在一条直线上,以点O为端点在直线AB的同一侧作射线,,使.
(1)如图①,若平分,求的度数;
(2)如图②,将绕点O按逆时针方向转动到某个位置时,使得所在射线把分成两个角.
①若,求的度数;
②若(n为正整数),直接用含n的代数式表示.
19.如图,在内.
(1)如果和都是直角.
①若,求的度数;
②猜想与的数量关系;
(2)如果,,求的度数(用含、的式子表示).
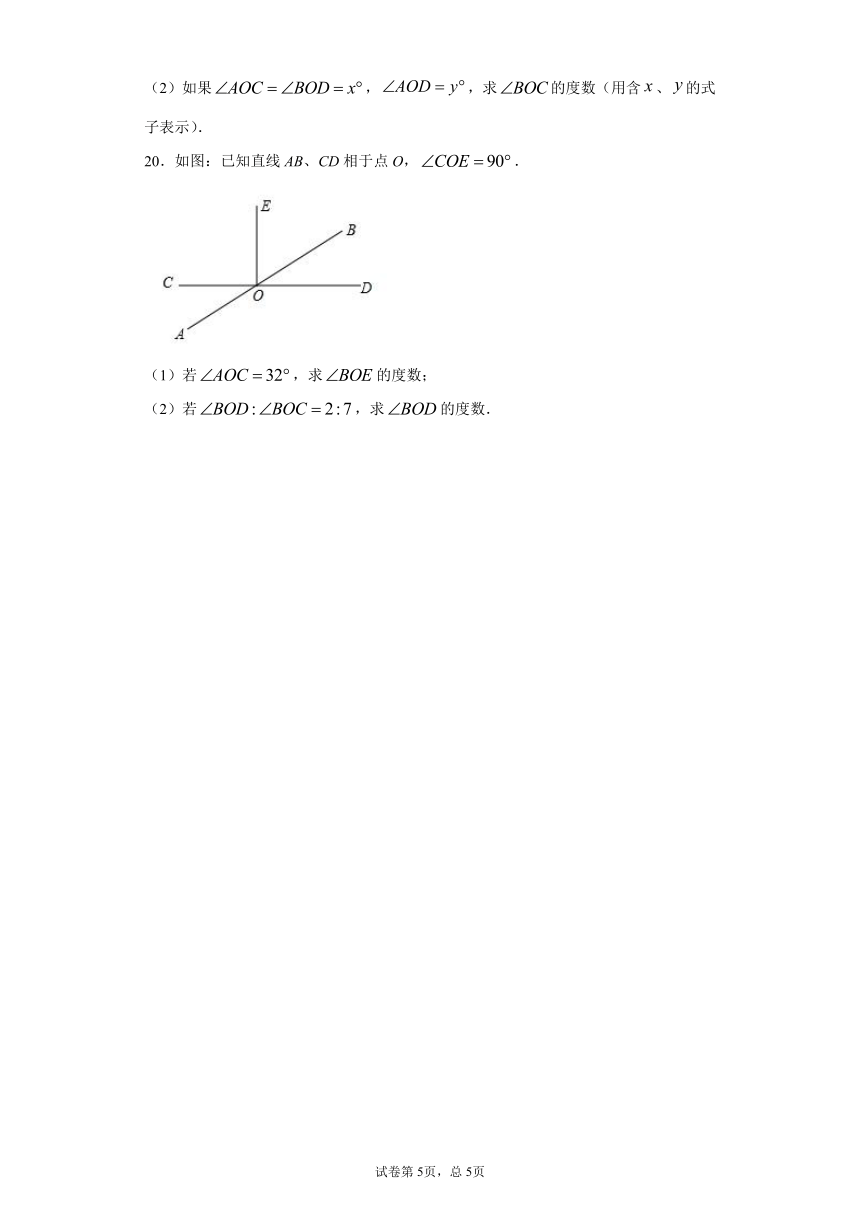
20.如图:已知直线AB、CD相于点O,.
(1)若,求的度数;
(2)若,求的度数.
参考答案
1.B
2.B
3.B
4.A
5.B
6.C
7.C
8.D
9.D
10.C
11.
12.
13.79°
14.56°35′43″
15.145
16.
17.(1)∠COE,∠AOD,∠BOC;(2)∠AOD=148°,∠BOF=122°;(3)90°,见解析
【详解】
解:(1)由直线与相交于点
∴∠DOE+∠COE=180°;∠BOD+∠AOD=180°
又∵平分
∴∠DOE=∠BOD
∴∠DOE+∠AOD=180°
又∵∠AOD=∠BOC
∴∠DOE+∠BOC=180°
∴∠DOE的补角为∠COE,∠AOD,∠BOC;
(2)因为OD是∠BOE的平分线,∠BOD=∠BOE=32°,
所以∠AOD=180°-∠BOD=148°,
因为∠AOE=180°-∠BOE=116°,OF是∠AOE的平分线,
所以∠AOF=∠AOE=58°,
所以∠BOF=180°-∠AOF=122°
即∠AOD=148°,∠BOF=122°;
(3)因为OF,OD分别是∠AOE,∠BOE的平分线,
所以∠DOF=∠DOE+∠EOF
=∠BOE+∠EOA
=(∠BOE+∠EOA)
=×180°
=90°.
18.(1);(2)①;②.
【详解】
解:(1)∵平分,,
∴,
∴,
∴,
∴;
(2)①∵,
∴∠EOC+∠COD=∠BOD+∠COD,
∴∠EOC=∠BOD,
∵,,
∴,
∴,
∴,
∴;
②∵,
∴∠EOC+∠COD=∠BOD+∠COD,
∴∠EOC=∠BOD,
∵,,
∴,
∴,
∴,
∴.
19.(1)①;②;(2)
【详解】
解:(1)①∵和都是直角,,
∴,
∴;
②猜想.
证明:∵,
∴,
∵,
∴;
(2)类比②可得:,
∵,
∴,
∵,
∴.
20.(1)58°;(2)40°
【详解】
解:(1)直线AB、CD相交于点O
(2),
.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,∠AOB=∠COD=90°,若∠BOD=150°,则∠BOC的度数为( )
A.150° B.120° C.90° D.60°
2.若与互补(),则与的关系是( )
A.互补 B.互余 C.和为 D.和为
3.如图,三角板中是直角,的顶点在直尺的边上,下面结论错误的是( )
A.与互余 B.
C. D.
4.已知∠1=39°15′,则∠1的余角为( ).
A.50°45′ B.50°85′ C.60°45′ D.60°85′
5.下列说法①互为相反数的两个数的同一偶数次方相等; ②与是同类项;③若关于x的方程的解是-2,则a的值是0;④一个角的补角一定大于这个角.其中正确的结论有几个?( )
A.1 B.2 C.3 D.4
6.已知:∠,∠,∠,则下列说法正确的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.∠1、∠2、∠3互不相等
7.如图,,,则的度数为( )
A. B. C. D.
8.如图,,在下面的四个式子中:①;② ;③;④,可以表示为 的补角的式子的个数是( )
A.1 B.2 C.3 D.4
9.如图,,以为一边作,则的度数为( )
A. B. C.或 D.或
10.如图,若,则下列结论一定正确的是( )
A. B.
C. D.
二、填空题
11.一副三角板如图摆放,若,则的度数是__________.
12.已知的余角是,则为________°.
13.如图,某市有三个中学A,B,O.中学A在中学O的北偏东61°15′的方向上,中学B在中学O的南偏东39°45′的方向上,则∠AOB的度数是_____.
14.如图,在直角∠AOB的内部作射线OC,若∠AOC=33°24′17″,则∠BOC=_____.
15.一副三角板如图放置(直角顶点叠放在一起),若,则______度.
16.如图,某一时刻在灯塔O处观测到游轮A在它的北偏西30°方向,同时又观测到货轮B在它的北偏东45°方向,则∠AOB的度数是_____°.
三、解答题
17.如图,直线与相交于点,,分别是,的平分线.
(1)写出的补角;
(2)若,求和的度数;
(3)射线与之间的夹角等于多少度?请说明理由.
18.已知点A,B,O在一条直线上,以点O为端点在直线AB的同一侧作射线,,使.
(1)如图①,若平分,求的度数;
(2)如图②,将绕点O按逆时针方向转动到某个位置时,使得所在射线把分成两个角.
①若,求的度数;
②若(n为正整数),直接用含n的代数式表示.
19.如图,在内.
(1)如果和都是直角.
①若,求的度数;
②猜想与的数量关系;
(2)如果,,求的度数(用含、的式子表示).
20.如图:已知直线AB、CD相于点O,.
(1)若,求的度数;
(2)若,求的度数.
参考答案
1.B
2.B
3.B
4.A
5.B
6.C
7.C
8.D
9.D
10.C
11.
12.
13.79°
14.56°35′43″
15.145
16.
17.(1)∠COE,∠AOD,∠BOC;(2)∠AOD=148°,∠BOF=122°;(3)90°,见解析
【详解】
解:(1)由直线与相交于点
∴∠DOE+∠COE=180°;∠BOD+∠AOD=180°
又∵平分
∴∠DOE=∠BOD
∴∠DOE+∠AOD=180°
又∵∠AOD=∠BOC
∴∠DOE+∠BOC=180°
∴∠DOE的补角为∠COE,∠AOD,∠BOC;
(2)因为OD是∠BOE的平分线,∠BOD=∠BOE=32°,
所以∠AOD=180°-∠BOD=148°,
因为∠AOE=180°-∠BOE=116°,OF是∠AOE的平分线,
所以∠AOF=∠AOE=58°,
所以∠BOF=180°-∠AOF=122°
即∠AOD=148°,∠BOF=122°;
(3)因为OF,OD分别是∠AOE,∠BOE的平分线,
所以∠DOF=∠DOE+∠EOF
=∠BOE+∠EOA
=(∠BOE+∠EOA)
=×180°
=90°.
18.(1);(2)①;②.
【详解】
解:(1)∵平分,,
∴,
∴,
∴,
∴;
(2)①∵,
∴∠EOC+∠COD=∠BOD+∠COD,
∴∠EOC=∠BOD,
∵,,
∴,
∴,
∴,
∴;
②∵,
∴∠EOC+∠COD=∠BOD+∠COD,
∴∠EOC=∠BOD,
∵,,
∴,
∴,
∴,
∴.
19.(1)①;②;(2)
【详解】
解:(1)①∵和都是直角,,
∴,
∴;
②猜想.
证明:∵,
∴,
∵,
∴;
(2)类比②可得:,
∵,
∴,
∵,
∴.
20.(1)58°;(2)40°
【详解】
解:(1)直线AB、CD相交于点O
(2),
.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
