青岛版 七下 13.1三角形同步课时训练(word版含答案)
文档属性
| 名称 | 青岛版 七下 13.1三角形同步课时训练(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 356.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 19:43:17 | ||
图片预览




文档简介
13.1三角形同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在下列长度的三条线段中,能组成三角形的是( )
A. B. C. D.
2.已知三角形的两边长分别是4和9,则此三角形第三条边的长可能是( )
A.3 B.4 C.6 D.15
3.已知三角形两边长分别为4和8,则该三角形第三边的长可能是( )
A.4 B.5 C.12 D.13
4.如图所示,已知G为直角△ABC的重心,,且,,则△AGD的面积是( )
A.9cm2 B.12cm2 C.18cm2 D.20cm2
5.如果一个三角形的两边长分别为和,则第三边的长可以是( )
A. B. C. D.
6.如图,在中,,,为中线,则与的周长之差为( )
A.1 B.2 C.3 D.4
7.为了估计池塘A,B两点之间的距离,小明在池塘的一侧选取一点C,测得AC=3m,BC=6m,则A,B两点之间的距离可能是( )
A.11m B.9m C.7m D.3m
8.如图,在中,,分别是边上的中线与高,,的面积为,则的长为( )
A. B. C. D.
9.如图,三角形中,,于点,则下列线段关系成立的是( )
A. B.
C. D.
10.如图,是的平分线,,,则等于( )
A.75° B.70° C.65° D.60°
二、填空题
11.如图,已知:,,平分,,则的度数是______.
12.已知在中,,,则边BC的长度的取值范围是___________.
13.如图,点依次在直线上,射线绕点O以每秒的速度顺时针旋转,同时射线绕点O以每秒的速度逆时针旋转,直线保持不动,设旋转时间为t秒,现以射线中两条为边组成一个角,使射线为该角的角平分线,此时t的值为_______.
14.如图,若,点E在直线的上方,连接,延长交于点F,已知,,则_________°.
15.如图,已知、分别为的角平分线、高线,若,,则的度数为__________.
16.如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为_____.
三、解答题
17.如图,射线在钝角的内部,且分,平分.
(1)当与重合时,求得度数;
(2)若,求的度数;
(3)若,求的度数(用含n的代数式表示).
18.如图所示,直线,相交于点,平分,射线在内部.
(1)若,求的度数.
(2)若平分,请直接写出图中所有互余的角.
(3)若,求的度数.
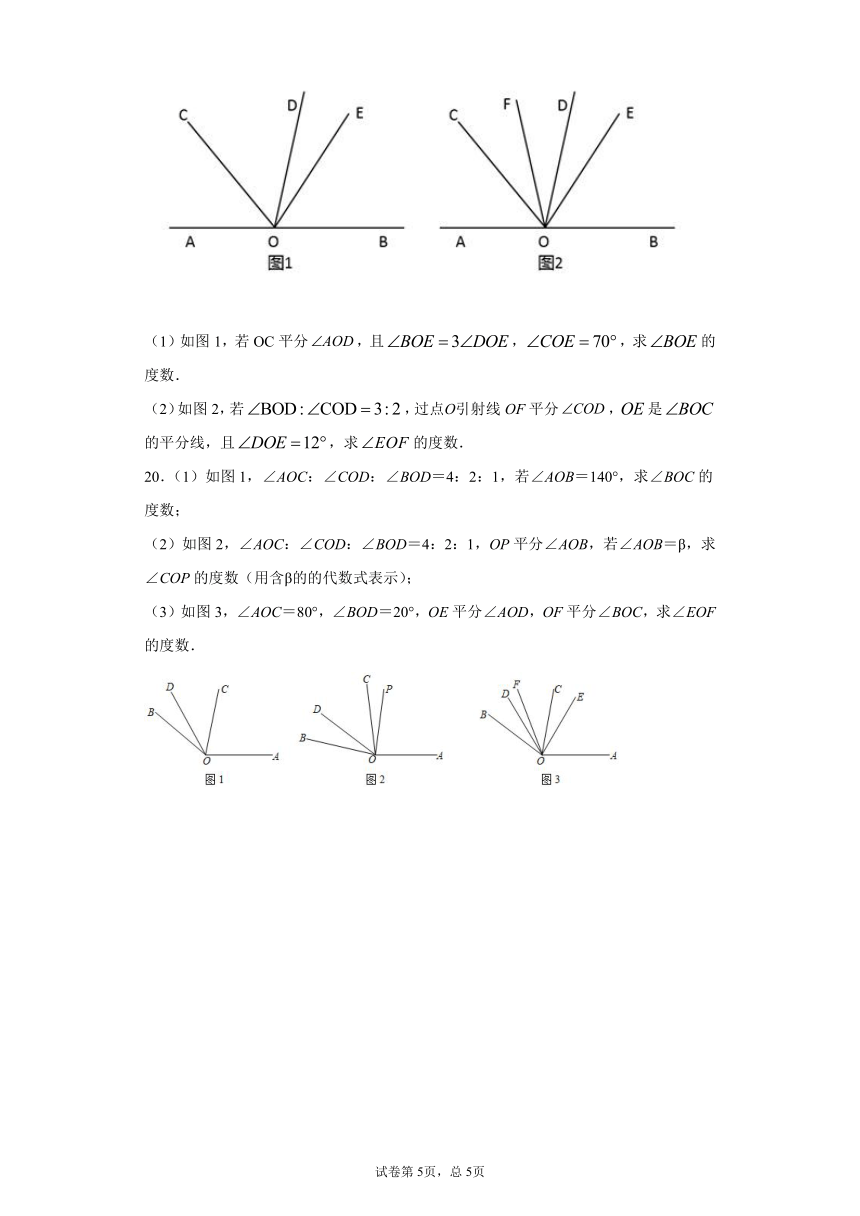
19.已知О为直线AB上一点,过点O向直线AB上方引三条射线OC、OD、OE.
(1)如图1,若OC平分,且,,求的度数.
(2)如图2,若,过点О引射线OF平分,是的平分线,且,求的度数.
20.(1)如图1,∠AOC:∠COD:∠BOD=4:2:1,若∠AOB=140°,求∠BOC的度数;
(2)如图2,∠AOC:∠COD:∠BOD=4:2:1,OP平分∠AOB,若∠AOB=β,求∠COP的度数(用含β的的代数式表示);
(3)如图3,∠AOC=80°,∠BOD=20°,OE平分∠AOD,OF平分∠BOC,求∠EOF的度数.
参考答案
1.A
2.C
3.B
4.A
5.C
6.B
7.C
8.B
9.C
10.D
11.40°
12.
13.15s或12s或24s
14.134
15.
16.14°
17.(1)120°;(2)10°;(3)n°-90°
【详解】
解:(1)如图(1),
∵OQ平分∠AOC,且点Q与点B重合,
∴∠AOB=∠BOC=∠AOC,
∵∠AOB+∠AOC=180°,
∴∠AOC+∠AOC=180°,
∴∠AOC=120°;
(2)如图(2),
∵∠AOC=100°,
又∵∠AOB+∠AOC=180°,
∴∠AOB=80°,
∵OP平分∠AOB,
∴∠AOP=40°,
∵OQ平分∠AOC,
∴∠AOQ=50°,
∴∠POQ=∠AOQ-∠AOP=50°-40°=10°;
(3)∵∠AOC=n°,
∴∠AOB+∠AOC=180°,
∴∠AOB=180°-n°,
∵OQ平分∠AOC,
∴∠AOQ=∠AOC=,
∵OP平分∠AOB,
∴∠AOP=∠AOB==,
∴∠POQ=∠AOQ-∠AOP
=
=.
18.(1);(2)与;与;与;与;(3)
【详解】
(1)
(2),
,
,
,
,
.
(3),
,
,
,
,
,
,
19.(1)60°;(2)36°
【详解】
解:(1)设∠DOE=x,则∠BOE=3x,
∴∠AOD=180°﹣4x,
∵OC平分∠AOD,
∴∠COD= ∠AOD=90°﹣2x,
∵∠COE=∠COD+∠DOE=90°﹣2x+x=90°﹣x=70°,
∴x=20°,
∴∠BOE=3x=60°;
(2)设∠BOD=3k,∠COD=2k,则∠BOC=5k,
∵OF平分,平分,
∴∠COF=∠FOD=k,∠COE=∠BOE=k,
∵∠DOE=∠COE﹣∠COD=k﹣2k=k=12°,
∴k=24°,
∴∠EOF=∠FOD+∠DOE=24°+12°=36°.
20.(1)60°;(2)β;(3)50°
【详解】
解:(1)由∠AOC:∠COD:∠BOD=4:2:1,
设∠BOD=x°,
则∠AOC=4x°,∠COD=2x°,
∵∠AOB=140°,
∴x+2x+4x=140,
解得:x=20,
∴∠BOD=20°,∠COD=40°,∠AOC=80°,
∴∠BOC=20°+40°=60°;
(2)设∠BOD=x°,
则∠AOC=4x°,∠COD=2x°,
∴x+2x+4x=β,
∴x=β,
∴∠AOC=β;
∵OP平分∠AOB,
∴∠AOP=,
∴∠COP=β﹣=β;
(3)∵OF平分∠BOC,∠BOD=20°,
∴∠COF=(∠BOD+∠COD)=10°+∠COD,
∵OE平分∠AOD,∠AOC=80°,
∴∠AOE=(∠AOC+∠COD)=40°+∠COD,
∴∠COE=∠AOC﹣∠AOE=80°﹣(40°+∠COD)=40°﹣∠COD,
∴∠EOF=∠COE+∠COF=40°﹣∠COD+10°+∠COD=50°.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在下列长度的三条线段中,能组成三角形的是( )
A. B. C. D.
2.已知三角形的两边长分别是4和9,则此三角形第三条边的长可能是( )
A.3 B.4 C.6 D.15
3.已知三角形两边长分别为4和8,则该三角形第三边的长可能是( )
A.4 B.5 C.12 D.13
4.如图所示,已知G为直角△ABC的重心,,且,,则△AGD的面积是( )
A.9cm2 B.12cm2 C.18cm2 D.20cm2
5.如果一个三角形的两边长分别为和,则第三边的长可以是( )
A. B. C. D.
6.如图,在中,,,为中线,则与的周长之差为( )
A.1 B.2 C.3 D.4
7.为了估计池塘A,B两点之间的距离,小明在池塘的一侧选取一点C,测得AC=3m,BC=6m,则A,B两点之间的距离可能是( )
A.11m B.9m C.7m D.3m
8.如图,在中,,分别是边上的中线与高,,的面积为,则的长为( )
A. B. C. D.
9.如图,三角形中,,于点,则下列线段关系成立的是( )
A. B.
C. D.
10.如图,是的平分线,,,则等于( )
A.75° B.70° C.65° D.60°
二、填空题
11.如图,已知:,,平分,,则的度数是______.
12.已知在中,,,则边BC的长度的取值范围是___________.
13.如图,点依次在直线上,射线绕点O以每秒的速度顺时针旋转,同时射线绕点O以每秒的速度逆时针旋转,直线保持不动,设旋转时间为t秒,现以射线中两条为边组成一个角,使射线为该角的角平分线,此时t的值为_______.
14.如图,若,点E在直线的上方,连接,延长交于点F,已知,,则_________°.
15.如图,已知、分别为的角平分线、高线,若,,则的度数为__________.
16.如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为_____.
三、解答题
17.如图,射线在钝角的内部,且分,平分.
(1)当与重合时,求得度数;
(2)若,求的度数;
(3)若,求的度数(用含n的代数式表示).
18.如图所示,直线,相交于点,平分,射线在内部.
(1)若,求的度数.
(2)若平分,请直接写出图中所有互余的角.
(3)若,求的度数.
19.已知О为直线AB上一点,过点O向直线AB上方引三条射线OC、OD、OE.
(1)如图1,若OC平分,且,,求的度数.
(2)如图2,若,过点О引射线OF平分,是的平分线,且,求的度数.
20.(1)如图1,∠AOC:∠COD:∠BOD=4:2:1,若∠AOB=140°,求∠BOC的度数;
(2)如图2,∠AOC:∠COD:∠BOD=4:2:1,OP平分∠AOB,若∠AOB=β,求∠COP的度数(用含β的的代数式表示);
(3)如图3,∠AOC=80°,∠BOD=20°,OE平分∠AOD,OF平分∠BOC,求∠EOF的度数.
参考答案
1.A
2.C
3.B
4.A
5.C
6.B
7.C
8.B
9.C
10.D
11.40°
12.
13.15s或12s或24s
14.134
15.
16.14°
17.(1)120°;(2)10°;(3)n°-90°
【详解】
解:(1)如图(1),
∵OQ平分∠AOC,且点Q与点B重合,
∴∠AOB=∠BOC=∠AOC,
∵∠AOB+∠AOC=180°,
∴∠AOC+∠AOC=180°,
∴∠AOC=120°;
(2)如图(2),
∵∠AOC=100°,
又∵∠AOB+∠AOC=180°,
∴∠AOB=80°,
∵OP平分∠AOB,
∴∠AOP=40°,
∵OQ平分∠AOC,
∴∠AOQ=50°,
∴∠POQ=∠AOQ-∠AOP=50°-40°=10°;
(3)∵∠AOC=n°,
∴∠AOB+∠AOC=180°,
∴∠AOB=180°-n°,
∵OQ平分∠AOC,
∴∠AOQ=∠AOC=,
∵OP平分∠AOB,
∴∠AOP=∠AOB==,
∴∠POQ=∠AOQ-∠AOP
=
=.
18.(1);(2)与;与;与;与;(3)
【详解】
(1)
(2),
,
,
,
,
.
(3),
,
,
,
,
,
,
19.(1)60°;(2)36°
【详解】
解:(1)设∠DOE=x,则∠BOE=3x,
∴∠AOD=180°﹣4x,
∵OC平分∠AOD,
∴∠COD= ∠AOD=90°﹣2x,
∵∠COE=∠COD+∠DOE=90°﹣2x+x=90°﹣x=70°,
∴x=20°,
∴∠BOE=3x=60°;
(2)设∠BOD=3k,∠COD=2k,则∠BOC=5k,
∵OF平分,平分,
∴∠COF=∠FOD=k,∠COE=∠BOE=k,
∵∠DOE=∠COE﹣∠COD=k﹣2k=k=12°,
∴k=24°,
∴∠EOF=∠FOD+∠DOE=24°+12°=36°.
20.(1)60°;(2)β;(3)50°
【详解】
解:(1)由∠AOC:∠COD:∠BOD=4:2:1,
设∠BOD=x°,
则∠AOC=4x°,∠COD=2x°,
∵∠AOB=140°,
∴x+2x+4x=140,
解得:x=20,
∴∠BOD=20°,∠COD=40°,∠AOC=80°,
∴∠BOC=20°+40°=60°;
(2)设∠BOD=x°,
则∠AOC=4x°,∠COD=2x°,
∴x+2x+4x=β,
∴x=β,
∴∠AOC=β;
∵OP平分∠AOB,
∴∠AOP=,
∴∠COP=β﹣=β;
(3)∵OF平分∠BOC,∠BOD=20°,
∴∠COF=(∠BOD+∠COD)=10°+∠COD,
∵OE平分∠AOD,∠AOC=80°,
∴∠AOE=(∠AOC+∠COD)=40°+∠COD,
∴∠COE=∠AOC﹣∠AOE=80°﹣(40°+∠COD)=40°﹣∠COD,
∴∠EOF=∠COE+∠COF=40°﹣∠COD+10°+∠COD=50°.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
