新人教A版高中数学必修第二册:表面积和体积
文档属性
| 名称 | 新人教A版高中数学必修第二册:表面积和体积 |
|
|
| 格式 | zip | ||
| 文件大小 | 951.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 00:00:00 | ||
图片预览




文档简介
授课主题:表面积和体积
教学目标
1.能根据柱、锥、台的结构特征,并结合它们的展开图,推导其表面积的计算公式.2.领会柱、锥、台、球体的表面积和体积公式等知识.3.能应用公式求解相关问题.4.了解球的表面积和体积的计算公式.5.能运用球的面积和体积公式灵活解决实际问题.
教学内容
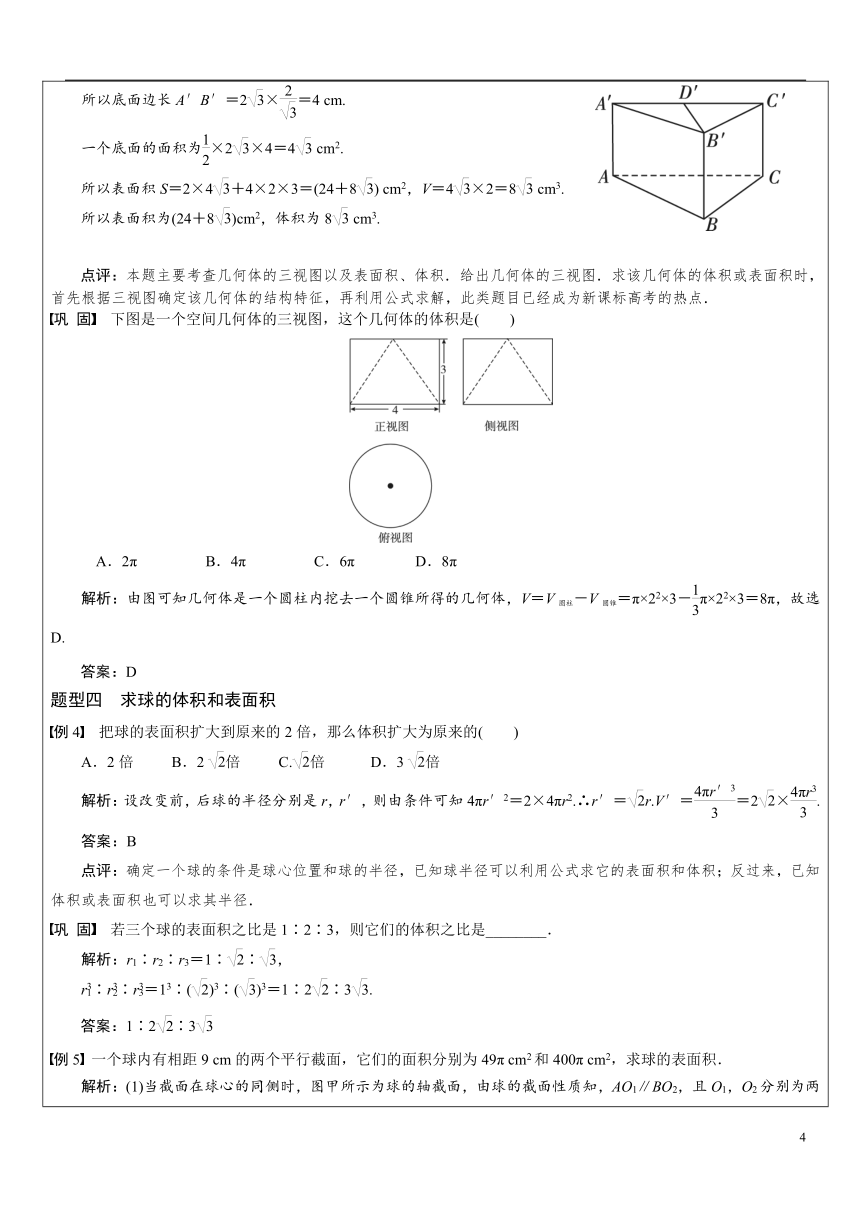
表面积公式图形表面积公式多面体多面体的表面积就是各个面的面积的和,也就是展开图的面积旋转体圆柱底面积:S底=πr2侧面积:S侧=2πrl表面积:S=2πrl+2πr2圆锥底面积:S底=πr2侧面积:S侧=πrl表面积:S=πrl+πr2圆台上底面面积:S上底=πr′2下底面面积:S下底=πr2侧面积:S侧=πl(r+r′)表面积:S=π(r′2+r2+r′l+rl)2.体积公式(1)柱体:柱体的底面面积为S,高为h,则V=Sh.(2)锥体:锥体的底面面积为S,高为h,则V=Sh.(3)台体:台体的上,下底面面积分别为S′,S,高为h,则V=(S′++S)h.3.球的体积
设球的半径为R,则球的体积V=πR3.4.球的表面积
设球的半径为R,则球的表面积S=4πR2,即球的表面积等于它的大圆面积的4倍.题型一 求空间几何体的表面积例1 如图所示的几何体是一棱长为4
cm的正方体,若在它的各个面的中心位置上,各打一个直径为2
cm、深为1
cm的圆柱形的孔,求打孔后的几何体的表面积是多少?(π取3.14)解析:由于正方体没有被打透,故打孔后的几何体的表面积为正方体的表面积加上六个圆柱的侧面积,正方体的表面积为16×6=96(cm2),一个圆柱的侧面积为2π×1×1=6.28(cm2),则打孔后几何体的表面积为96+6.28×6=133.68(cm2).点评:求几何体的表面积问题,通常将所给几何体分成基本的柱、锥、台,再通过这些基本柱、锥、台的表面积,进行求和或作差,从而获得几何体的表面积.巩
固 如下图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为( )A.3π
B.2π
C.π
D.4π答案:C题型二 求空间几何体的体积例2
三棱台ABCA1B1C1中,AB∶A1B1=1∶2,则三棱锥A1ABC,BA1B1C,CA1B1C1的体积之比为( )A.1∶1∶1
B.1∶1∶2C.1∶2∶4
D.1∶4∶4解析:设棱台的高为h,S△ABC=S,则S△A1B1C1=4S.∴VA1ABC=S△ABC·h=Sh,VCA1B1C1=S△A1B1C1·h=Sh.又V台=h(S+4S+2S)=Sh,∴VBA1B1C=V台-VA1ABC-VCA1B1C1=Sh--=Sh,∴体积比为1∶2∶4,∴应选C.答案:C点评:求台体体积的常用方法有三种:一是利用台体的体积公式来求解,这就需要知道台体的上、下底面积和高;二是抓住台体是由锥体截割而来的这一特征,把它还原成锥体,利用锥体体积公式来求其台体的体积;三是利用割补法来求其体积.巩
固 正方体ABCDA1B1C1D1中,O是上底面ABCD中心,若正方体的棱长为a,则三棱锥OAB1D1的体积为________.解析:画出正方体,平面AB1D1与对角线A1C的交点是对角线的三等分点,三棱锥OAB1D1的高h=a,V=Sh=××2a2×a=a3.三棱锥OAB1D1也可以看成三棱锥AOB1D1,显然它的高为AO,等腰三角形OB1D1为底面.答案:a3题型三 几何体表面积与体积公式的综合应用例3 一个正三棱柱的三视图如图所示(单位:cm),求这个正三棱柱的表面积与体积.解析:由三视图知直观图如右图所示,则高AA′=2
cm,底面高B′D′=2
cm,所以底面边长A′B′=2×=4
cm.一个底面的面积为×2×4=4
cm2.所以表面积S=2×4+4×2×3=(24+8)
cm2,V=4×2=8
cm3.所以表面积为(24+8)cm2,体积为8
cm3.点评:本题主要考查几何体的三视图以及表面积、体积.给出几何体的三视图.求该几何体的体积或表面积时,首先根据三视图确定该几何体的结构特征,再利用公式求解,此类题目已经成为新课标高考的热点.巩
固 下图是一个空间几何体的三视图,这个几何体的体积是( )A.2π
B.4π
C.6π
D.8π解析:由图可知几何体是一个圆柱内挖去一个圆锥所得的几何体,V=V圆柱-V圆锥=π×22×3-π×22×3=8π,故选D.答案:D题型四 求球的体积和表面积例4 把球的表面积扩大到原来的2倍,那么体积扩大为原来的( )A.2倍
B.2倍
C.倍
D.3倍解析:设改变前,后球的半径分别是r,r′,则由条件可知4πr′2=2×4πr2.∴r′=r.V′==2×.答案:B点评:确定一个球的条件是球心位置和球的半径,已知球半径可以利用公式求它的表面积和体积;反过来,已知体积或表面积也可以求其半径.巩
固 若三个球的表面积之比是1∶2∶3,则它们的体积之比是________.解析:r1∶r2∶r3=1∶∶,r∶r∶r=13∶()3∶()3=1∶2∶3.答案:1∶2∶3例5
一个球内有相距9
cm的两个平行截面,它们的面积分别为49π
cm2和400π
cm2,求球的表面积.解析:(1)当截面在球心的同侧时,图甲所示为球的轴截面,由球的截面性质知,AO1∥BO2,且O1,O2分别为两截面圆的圆心,则OO1⊥AO1,OO2⊥BO2.设球的半径为R.∵π·O2B2=49π,∴O2B=7(cm).∵π·O1A2=400π,∴O1A=20(cm).设OO1=x
cm,则OO2=(x+9)cm.在Rt△OO1A中,R2=x2+202,在Rt△OO2B中,R2=(x+9)2+72,∴x2+202=72+(x+9)2,解得x=15,∴R2=x2+202=252,∴R=25(cm).∴S球=4πR2=2
500π(cm2).∴球的表面积为2
500π
cm2.(2)当截面在球心的两侧时,图乙所示为球的轴截面,由球的截面性质知,O1A∥O2B,且O1,O2分别为两截面圆的圆心,则OO1⊥O1A,OO2⊥O2B.
设球的半径为R.∵π·O2B2=49π,∴O2B=7(cm).∵π·O1A2=400π,∴O1A=20(cm).设O1O=x
cm,则OO2=(9-x)cm.在Rt△OO1A中,R2=x2+400.在Rt△OO2B中,R2=(9-x)2+49.∴x2+400=(9-x)2+49,解得x=-15(cm),不合题意,舍去.综上所述,球的表面积为2
500π
cm2.点评:球的轴截面(过球心的截面)是将球的问题(立体几何问题)转化为平面问题(圆的问题)的关键,因此在解决球的有关问题时,我们必须抓住球的轴截面,并充分利用它来分析解决问题.巩
固 用与球心距离为2的平面去截球,若球的体积为36π,则所得截面圆的面积为________.解析:设球的半径为R,则πR3=36π,∴R=3.设截面圆的半径为r,则r2=32-22=5.∴截面圆的面积为5π.答案:5π题型五 球的内接、外切几何体问题例6 有三个球,第一个球内切于正方体,第二个球与这个正方体各条棱相切,第三个球过这个正方体的各个顶点,求这三个球的表面积之比.解析:作出截面图,分别求出三个球的半径.设正方体的棱长为a.(1)正方体的内切球球心是正方体的中心,切点是六个正方形的中心,经过四个切点及球心作截面,如图甲,所以有2r1=a,r1=,所以S1=4πr21=πa2.(2)球与正方体的各棱的切点在每条棱的中点,过球心作正方体的对角面得截面,如图乙,所以有2r2=a,r2=a,所以S2=4πr22=2πa2.(3)正方体的各个顶点在球面上,过球心作正方体的对角面得截面,如图丙,所以有2r3=a,r3=a,所以S3=4πr23=3πa2.综上可得S1∶S2∶S3=1∶2∶3.点评:解决与球有关组合体问题,可通过画过球心的截面来分析.下列结论常用:①正方体的8个顶点在同一个球面,则正方体的体对角线是球的直径;②球与正方体的六个面均相切,则球的直径等于正方体的棱长;③球与正方体的8条棱均相切,则球的直径是正方体的面对角线.巩
固 一个六棱柱的底面是正六边形,其侧棱垂直于底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为,底面周长为3,则这个球的体积为________.解析:设正六棱柱的底面边长为x,则6x=3.∴x=.设正六棱柱的高为h,由其体积V=知=6××2×h.∴h=.∵正六棱柱外接球的直径恰好是正六棱柱体的对角线长,∴2R=.∴R=1.∴V球=.答案:题型六 球的体积、表面积的综合应用例7 一个直径为32
cm的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9
cm,则此球的半径为________cm.解析:V=Sh=πr2h=πR3,R==12
cm.答案:12巩
固 半径为R的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是________.解析:设圆柱的底面半径为r,则
S侧=2πr·2=4π.当S侧取得最大值时,r2=R2-r2,即r=R.则4πR2-2πR2=2πR2.答案:2πR21.棱长都是1的三棱锥的表面积为( )A.
B.2
C.3
D.4解析:S表=4S正△=4×=.答案:A2.圆锥的母线长扩大n倍,底面半径缩小n倍,那么它的侧面积变为原来的( )A.1倍
B.n倍
C.n2倍
D.倍解析:圆锥侧面积S=πrl,设r缩小n倍,l扩大n倍后S′=π×r×nl=πrl=S,侧面积保持不变.答案:A3.某几何体的三视图如图所示,则该几何体的体积为( )A.
B.
C.200
D.240答案:C4.若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的全面积是( )A.3π
B.3π
C.6π
D.9π
解析:设圆锥底面半径为R,∴·2R·R=,∴R=1,母线l长为2,∴S全=πR2+πRl=π+2π=3π.答案:A
5.长方体三个面的面积分别为2,6和9,则长方体的体积是( )A.6
B.3
C.11
D.12解析:设长方体长、宽、高分别为a,b,c,不妨设ab=2,ac=6,bc=9,相乘得(abc)2=108,∴V=abc=6.答案:A6.一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V1,V2,V3,V4,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有( )A.V1B.V1D.V2B.1∶(-1) C.1∶9
D.∶2解析:由题意可知,截面面积与底面面积之比为1∶3,∴截面半径与底面半径之比为1∶,∴这两段母线长之比为1∶-1.答案:B8.某四棱台三视图如图所示,则该四棱台的体积是( )A.4
B.
C.
D.6答案:B9.(1)边长为a的正三角形、正方形、正六边形的面积分别为__________.(2)
圆柱的底面半径是2,高(母线长)为3,下底面积为________;侧面积为________;表面积为________.(3)
圆台上底面半径为2,下底面半径为3,母线长为4,上底面积为
______;下底面积为______;侧面积为________;表面积为________.(4)
正方体的表面积为100,对角线长度为________.答案:(1)
a2 a2 a2(2)
4π 12π 20π(3)
4π 9π 20π 33π(4)
510.若等腰直角三角形的直角边长为2,则以一直角边所在的直线为轴旋转一周所得的几何体体积是________.解析:所得旋转体是底面半径为2,高为2的圆锥,体积V=π×22×2=.答案:11.若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于________.解析:通过三视图还原三棱柱直观图如图所示,通过正视图可以得出该三棱柱底面边长为2,侧棱长为1,三个侧面为矩形,上下底面为正三角形,∴S表=3×(2×1)+2×=6+2.答案:6+212.如图,已知圆柱体底面圆的半径为
cm,高为2
cm,AB、CD分别是两底面的直径,AD、BC是母线,若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短路线的长度是________cm(结果保留根式).答案:213.某几何体的三视图如图所示,则其体积为________.答案:14.圆台的上、下底面半径分别是10
cm和20
cm,它的侧面展开图的扇环的圆心角是180°,那么圆台的表面积是多少?分析:由题目可获取以下主要信息:①求圆台的表面积应考虑上、下底面及侧面积;②上、下底面面积易得,主要求侧面积.解答本题可先把空间问题转化为平面问题,即在展开图内求母线的长,再进一步代入侧面积公式求出侧面积,进而求出表面积.解析:如图所示,设圆台的上底面周长为C,因为扇环的圆心角是180°,故C=π·SA=2π×10,∴SA=20,同理可得SB=40,∴AB=SB-SA=20,∴S表面积=S侧+S上+S下=π(r1+r2)·AB+πr+πr=π(10+20)×20+π×102+π×202=1
100π(cm2).故圆台的表面积为1
100π
cm2.15.如右图所示,在底半径为2,母线长为4的圆锥中内接一个高为的圆柱,求圆柱的表面积.解析:圆锥高h==2,画轴截面积图(如右图),则=.故圆锥内接圆柱的底半径x=1.则圆柱的表面积S=2π×12+2π×1×=(2+2)π.答案:(2+2
)π1.圆柱、圆锥、圆台的侧面积分别是它们侧面展开图面积,因此弄清侧面展开图的形状及侧面展开图中各线段与原旋转体的关系,是掌握它们的侧面积公式及解有关问题的关键.2.计算柱体、锥体和台体的体积,关键是根据条件找出相应的底面面积和高,要充分运用多面体的有关截面及旋转体的轴截面,将空间问题转化为平面问题.3.球的体积比等于半径的立方比,表面积之比等于半径的平方比.4.球体与多面体的组合体的解决关键是作出以球的轴截面为主的球及多面体的轴截面图,实现空间几何向平面几何的转化.1.若一个球的内接正方体的表面积为54,则球的表面积是( )A.27π
B.18πC.9π
D.54π解析:设正方体的棱长为a,∴6a2=54,∴a=3,设球的半径为R,∴(2R)2=3a2,4R2=27,S=4πR2=27π.答案:A2.若两个球的表面积之比为1∶4,则这两个球的体积之比为( )A.1∶2
B.1∶4
C.1∶8
D.1∶16答案:C3.若球的大圆周长是C,则这个球的表面积是( )A.
B.
C.
D.2πC2解析:由2πR=C,得R=,∴S球=4πR2=.答案:C4.两个球的表面积之差为48π,它们的大圆周长之和为12π,这两个球的半径之差为( )A.4
B.3
C.2
D.1解析:由4πR2-4πr2=48π,2πR+2πr=12π,得R-r=2.答案:C5.正方体的内切球和外接球的半径之比为( )A.∶1
B.∶2
C.2∶
D.∶3解析:内切球与外接球的半径之比为正方体棱长与体对角线长之比,即为∶3.答案:D6.用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( )A.
B.
C.8π
D.解析:截面面积为π,则该小圆的半径为1,设球的半径为R,则R2=12+12=2,∴R=,V=πR3=.答案:B7.(1)
一个球的半径是2,它的体积为________.(2)
一个球的半径是2,它的表面积是________.(3)
一个球的表面积变为原来的一半,半径是原来的________倍.(4)
一个球的体积是36π,它的表面积是________.答案:(1)
(2)
16π(3)
(4)
36π8.两个半径为1的铁球,熔化成一个大球,这个大球的半径是________.解析:设大球半径为R,则πR3=π×13+π×13,∴R3=2,R=.答案:9.球的半径扩大为原来的2倍,它的体积扩大为原来的________
倍.解析:设球原来半径为R,则扩大后半径为2R,V球原=πR3,V球扩=π(2R)3=8V球原.答案:810.将一钢球放入底面半径为3
cm的圆柱形玻璃容器中,水面升高4
cm,则钢球的半径是________.解析:圆柱形玻璃容器中水面升高4
cm,则钢球的体积为V=π×32×4=36π,即有πR3=36π,∴R=3.答案:3
cm11.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1、2、3,则此球的表面积为________.答案:14π12.球面上有四个点P,A,B,C,如果PA,PB,PC两两互相垂直,且PA=PB=PC=a,求这个球的表面积.解析:PA,PB,PC两两互相垂直,将三棱锥补成一个以P为顶点的正方体,且PA=PB=PC=a,∴正方体的对角线长就是球的直径,∴2R=a,R=a,∴这个球的表面积为S球=4πR2=4π2=3πa2.13.把直径分别为6
cm,8
cm,10
cm的三个铜球熔制成一个较大的铜球,再把球削成一个棱长最长的正方体,求此正方体的体积.解析:设熔制后的大铜球半径为r,则π(33+43+53)=πr3,∴r=6
cm.据题意:此正方体为球的内接正方体,球的直径即为正方体对角线的长,故正方体的棱长a===4
cm.∴V正方体=a3=(4)3=192
cm3.14.如图所示,一个容器的盖子用一个正四棱台和一个球焊接而成,球的半径为R,正四棱台的上、下底面边长分别为2.5R和3R,斜高为0.6R.(1)求这个容器盖子的表面积(用R表示,焊接处对面积的影响忽略不计);解析:由题意,知S正四棱台=4××(2.5R+3R)×0.6R+(2.5R)2+(3R)2=21.85R2,S球=4πR2,所以这个盖子的表面积为S表=(21.85+4π)R2,(2)若R=2
cm,为盖子涂色时所用的涂料每0.4
kg可以涂1
m2,计算为100个这样的盖子涂色用涂料多少千克(精确到0.1
kg).解析:取R=2,π=3.14,得S表=137.64(cm2).100个这样的盖子共需涂料约为(137.64×100)÷10
000×0.4≈0.6
kg.
PAGE
教学目标
1.能根据柱、锥、台的结构特征,并结合它们的展开图,推导其表面积的计算公式.2.领会柱、锥、台、球体的表面积和体积公式等知识.3.能应用公式求解相关问题.4.了解球的表面积和体积的计算公式.5.能运用球的面积和体积公式灵活解决实际问题.
教学内容
表面积公式图形表面积公式多面体多面体的表面积就是各个面的面积的和,也就是展开图的面积旋转体圆柱底面积:S底=πr2侧面积:S侧=2πrl表面积:S=2πrl+2πr2圆锥底面积:S底=πr2侧面积:S侧=πrl表面积:S=πrl+πr2圆台上底面面积:S上底=πr′2下底面面积:S下底=πr2侧面积:S侧=πl(r+r′)表面积:S=π(r′2+r2+r′l+rl)2.体积公式(1)柱体:柱体的底面面积为S,高为h,则V=Sh.(2)锥体:锥体的底面面积为S,高为h,则V=Sh.(3)台体:台体的上,下底面面积分别为S′,S,高为h,则V=(S′++S)h.3.球的体积
设球的半径为R,则球的体积V=πR3.4.球的表面积
设球的半径为R,则球的表面积S=4πR2,即球的表面积等于它的大圆面积的4倍.题型一 求空间几何体的表面积例1 如图所示的几何体是一棱长为4
cm的正方体,若在它的各个面的中心位置上,各打一个直径为2
cm、深为1
cm的圆柱形的孔,求打孔后的几何体的表面积是多少?(π取3.14)解析:由于正方体没有被打透,故打孔后的几何体的表面积为正方体的表面积加上六个圆柱的侧面积,正方体的表面积为16×6=96(cm2),一个圆柱的侧面积为2π×1×1=6.28(cm2),则打孔后几何体的表面积为96+6.28×6=133.68(cm2).点评:求几何体的表面积问题,通常将所给几何体分成基本的柱、锥、台,再通过这些基本柱、锥、台的表面积,进行求和或作差,从而获得几何体的表面积.巩
固 如下图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为( )A.3π
B.2π
C.π
D.4π答案:C题型二 求空间几何体的体积例2
三棱台ABCA1B1C1中,AB∶A1B1=1∶2,则三棱锥A1ABC,BA1B1C,CA1B1C1的体积之比为( )A.1∶1∶1
B.1∶1∶2C.1∶2∶4
D.1∶4∶4解析:设棱台的高为h,S△ABC=S,则S△A1B1C1=4S.∴VA1ABC=S△ABC·h=Sh,VCA1B1C1=S△A1B1C1·h=Sh.又V台=h(S+4S+2S)=Sh,∴VBA1B1C=V台-VA1ABC-VCA1B1C1=Sh--=Sh,∴体积比为1∶2∶4,∴应选C.答案:C点评:求台体体积的常用方法有三种:一是利用台体的体积公式来求解,这就需要知道台体的上、下底面积和高;二是抓住台体是由锥体截割而来的这一特征,把它还原成锥体,利用锥体体积公式来求其台体的体积;三是利用割补法来求其体积.巩
固 正方体ABCDA1B1C1D1中,O是上底面ABCD中心,若正方体的棱长为a,则三棱锥OAB1D1的体积为________.解析:画出正方体,平面AB1D1与对角线A1C的交点是对角线的三等分点,三棱锥OAB1D1的高h=a,V=Sh=××2a2×a=a3.三棱锥OAB1D1也可以看成三棱锥AOB1D1,显然它的高为AO,等腰三角形OB1D1为底面.答案:a3题型三 几何体表面积与体积公式的综合应用例3 一个正三棱柱的三视图如图所示(单位:cm),求这个正三棱柱的表面积与体积.解析:由三视图知直观图如右图所示,则高AA′=2
cm,底面高B′D′=2
cm,所以底面边长A′B′=2×=4
cm.一个底面的面积为×2×4=4
cm2.所以表面积S=2×4+4×2×3=(24+8)
cm2,V=4×2=8
cm3.所以表面积为(24+8)cm2,体积为8
cm3.点评:本题主要考查几何体的三视图以及表面积、体积.给出几何体的三视图.求该几何体的体积或表面积时,首先根据三视图确定该几何体的结构特征,再利用公式求解,此类题目已经成为新课标高考的热点.巩
固 下图是一个空间几何体的三视图,这个几何体的体积是( )A.2π
B.4π
C.6π
D.8π解析:由图可知几何体是一个圆柱内挖去一个圆锥所得的几何体,V=V圆柱-V圆锥=π×22×3-π×22×3=8π,故选D.答案:D题型四 求球的体积和表面积例4 把球的表面积扩大到原来的2倍,那么体积扩大为原来的( )A.2倍
B.2倍
C.倍
D.3倍解析:设改变前,后球的半径分别是r,r′,则由条件可知4πr′2=2×4πr2.∴r′=r.V′==2×.答案:B点评:确定一个球的条件是球心位置和球的半径,已知球半径可以利用公式求它的表面积和体积;反过来,已知体积或表面积也可以求其半径.巩
固 若三个球的表面积之比是1∶2∶3,则它们的体积之比是________.解析:r1∶r2∶r3=1∶∶,r∶r∶r=13∶()3∶()3=1∶2∶3.答案:1∶2∶3例5
一个球内有相距9
cm的两个平行截面,它们的面积分别为49π
cm2和400π
cm2,求球的表面积.解析:(1)当截面在球心的同侧时,图甲所示为球的轴截面,由球的截面性质知,AO1∥BO2,且O1,O2分别为两截面圆的圆心,则OO1⊥AO1,OO2⊥BO2.设球的半径为R.∵π·O2B2=49π,∴O2B=7(cm).∵π·O1A2=400π,∴O1A=20(cm).设OO1=x
cm,则OO2=(x+9)cm.在Rt△OO1A中,R2=x2+202,在Rt△OO2B中,R2=(x+9)2+72,∴x2+202=72+(x+9)2,解得x=15,∴R2=x2+202=252,∴R=25(cm).∴S球=4πR2=2
500π(cm2).∴球的表面积为2
500π
cm2.(2)当截面在球心的两侧时,图乙所示为球的轴截面,由球的截面性质知,O1A∥O2B,且O1,O2分别为两截面圆的圆心,则OO1⊥O1A,OO2⊥O2B.
设球的半径为R.∵π·O2B2=49π,∴O2B=7(cm).∵π·O1A2=400π,∴O1A=20(cm).设O1O=x
cm,则OO2=(9-x)cm.在Rt△OO1A中,R2=x2+400.在Rt△OO2B中,R2=(9-x)2+49.∴x2+400=(9-x)2+49,解得x=-15(cm),不合题意,舍去.综上所述,球的表面积为2
500π
cm2.点评:球的轴截面(过球心的截面)是将球的问题(立体几何问题)转化为平面问题(圆的问题)的关键,因此在解决球的有关问题时,我们必须抓住球的轴截面,并充分利用它来分析解决问题.巩
固 用与球心距离为2的平面去截球,若球的体积为36π,则所得截面圆的面积为________.解析:设球的半径为R,则πR3=36π,∴R=3.设截面圆的半径为r,则r2=32-22=5.∴截面圆的面积为5π.答案:5π题型五 球的内接、外切几何体问题例6 有三个球,第一个球内切于正方体,第二个球与这个正方体各条棱相切,第三个球过这个正方体的各个顶点,求这三个球的表面积之比.解析:作出截面图,分别求出三个球的半径.设正方体的棱长为a.(1)正方体的内切球球心是正方体的中心,切点是六个正方形的中心,经过四个切点及球心作截面,如图甲,所以有2r1=a,r1=,所以S1=4πr21=πa2.(2)球与正方体的各棱的切点在每条棱的中点,过球心作正方体的对角面得截面,如图乙,所以有2r2=a,r2=a,所以S2=4πr22=2πa2.(3)正方体的各个顶点在球面上,过球心作正方体的对角面得截面,如图丙,所以有2r3=a,r3=a,所以S3=4πr23=3πa2.综上可得S1∶S2∶S3=1∶2∶3.点评:解决与球有关组合体问题,可通过画过球心的截面来分析.下列结论常用:①正方体的8个顶点在同一个球面,则正方体的体对角线是球的直径;②球与正方体的六个面均相切,则球的直径等于正方体的棱长;③球与正方体的8条棱均相切,则球的直径是正方体的面对角线.巩
固 一个六棱柱的底面是正六边形,其侧棱垂直于底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为,底面周长为3,则这个球的体积为________.解析:设正六棱柱的底面边长为x,则6x=3.∴x=.设正六棱柱的高为h,由其体积V=知=6××2×h.∴h=.∵正六棱柱外接球的直径恰好是正六棱柱体的对角线长,∴2R=.∴R=1.∴V球=.答案:题型六 球的体积、表面积的综合应用例7 一个直径为32
cm的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9
cm,则此球的半径为________cm.解析:V=Sh=πr2h=πR3,R==12
cm.答案:12巩
固 半径为R的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是________.解析:设圆柱的底面半径为r,则
S侧=2πr·2=4π.当S侧取得最大值时,r2=R2-r2,即r=R.则4πR2-2πR2=2πR2.答案:2πR21.棱长都是1的三棱锥的表面积为( )A.
B.2
C.3
D.4解析:S表=4S正△=4×=.答案:A2.圆锥的母线长扩大n倍,底面半径缩小n倍,那么它的侧面积变为原来的( )A.1倍
B.n倍
C.n2倍
D.倍解析:圆锥侧面积S=πrl,设r缩小n倍,l扩大n倍后S′=π×r×nl=πrl=S,侧面积保持不变.答案:A3.某几何体的三视图如图所示,则该几何体的体积为( )A.
B.
C.200
D.240答案:C4.若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的全面积是( )A.3π
B.3π
C.6π
D.9π
解析:设圆锥底面半径为R,∴·2R·R=,∴R=1,母线l长为2,∴S全=πR2+πRl=π+2π=3π.答案:A
5.长方体三个面的面积分别为2,6和9,则长方体的体积是( )A.6
B.3
C.11
D.12解析:设长方体长、宽、高分别为a,b,c,不妨设ab=2,ac=6,bc=9,相乘得(abc)2=108,∴V=abc=6.答案:A6.一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V1,V2,V3,V4,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有( )A.V1
D.∶2解析:由题意可知,截面面积与底面面积之比为1∶3,∴截面半径与底面半径之比为1∶,∴这两段母线长之比为1∶-1.答案:B8.某四棱台三视图如图所示,则该四棱台的体积是( )A.4
B.
C.
D.6答案:B9.(1)边长为a的正三角形、正方形、正六边形的面积分别为__________.(2)
圆柱的底面半径是2,高(母线长)为3,下底面积为________;侧面积为________;表面积为________.(3)
圆台上底面半径为2,下底面半径为3,母线长为4,上底面积为
______;下底面积为______;侧面积为________;表面积为________.(4)
正方体的表面积为100,对角线长度为________.答案:(1)
a2 a2 a2(2)
4π 12π 20π(3)
4π 9π 20π 33π(4)
510.若等腰直角三角形的直角边长为2,则以一直角边所在的直线为轴旋转一周所得的几何体体积是________.解析:所得旋转体是底面半径为2,高为2的圆锥,体积V=π×22×2=.答案:11.若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于________.解析:通过三视图还原三棱柱直观图如图所示,通过正视图可以得出该三棱柱底面边长为2,侧棱长为1,三个侧面为矩形,上下底面为正三角形,∴S表=3×(2×1)+2×=6+2.答案:6+212.如图,已知圆柱体底面圆的半径为
cm,高为2
cm,AB、CD分别是两底面的直径,AD、BC是母线,若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短路线的长度是________cm(结果保留根式).答案:213.某几何体的三视图如图所示,则其体积为________.答案:14.圆台的上、下底面半径分别是10
cm和20
cm,它的侧面展开图的扇环的圆心角是180°,那么圆台的表面积是多少?分析:由题目可获取以下主要信息:①求圆台的表面积应考虑上、下底面及侧面积;②上、下底面面积易得,主要求侧面积.解答本题可先把空间问题转化为平面问题,即在展开图内求母线的长,再进一步代入侧面积公式求出侧面积,进而求出表面积.解析:如图所示,设圆台的上底面周长为C,因为扇环的圆心角是180°,故C=π·SA=2π×10,∴SA=20,同理可得SB=40,∴AB=SB-SA=20,∴S表面积=S侧+S上+S下=π(r1+r2)·AB+πr+πr=π(10+20)×20+π×102+π×202=1
100π(cm2).故圆台的表面积为1
100π
cm2.15.如右图所示,在底半径为2,母线长为4的圆锥中内接一个高为的圆柱,求圆柱的表面积.解析:圆锥高h==2,画轴截面积图(如右图),则=.故圆锥内接圆柱的底半径x=1.则圆柱的表面积S=2π×12+2π×1×=(2+2)π.答案:(2+2
)π1.圆柱、圆锥、圆台的侧面积分别是它们侧面展开图面积,因此弄清侧面展开图的形状及侧面展开图中各线段与原旋转体的关系,是掌握它们的侧面积公式及解有关问题的关键.2.计算柱体、锥体和台体的体积,关键是根据条件找出相应的底面面积和高,要充分运用多面体的有关截面及旋转体的轴截面,将空间问题转化为平面问题.3.球的体积比等于半径的立方比,表面积之比等于半径的平方比.4.球体与多面体的组合体的解决关键是作出以球的轴截面为主的球及多面体的轴截面图,实现空间几何向平面几何的转化.1.若一个球的内接正方体的表面积为54,则球的表面积是( )A.27π
B.18πC.9π
D.54π解析:设正方体的棱长为a,∴6a2=54,∴a=3,设球的半径为R,∴(2R)2=3a2,4R2=27,S=4πR2=27π.答案:A2.若两个球的表面积之比为1∶4,则这两个球的体积之比为( )A.1∶2
B.1∶4
C.1∶8
D.1∶16答案:C3.若球的大圆周长是C,则这个球的表面积是( )A.
B.
C.
D.2πC2解析:由2πR=C,得R=,∴S球=4πR2=.答案:C4.两个球的表面积之差为48π,它们的大圆周长之和为12π,这两个球的半径之差为( )A.4
B.3
C.2
D.1解析:由4πR2-4πr2=48π,2πR+2πr=12π,得R-r=2.答案:C5.正方体的内切球和外接球的半径之比为( )A.∶1
B.∶2
C.2∶
D.∶3解析:内切球与外接球的半径之比为正方体棱长与体对角线长之比,即为∶3.答案:D6.用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( )A.
B.
C.8π
D.解析:截面面积为π,则该小圆的半径为1,设球的半径为R,则R2=12+12=2,∴R=,V=πR3=.答案:B7.(1)
一个球的半径是2,它的体积为________.(2)
一个球的半径是2,它的表面积是________.(3)
一个球的表面积变为原来的一半,半径是原来的________倍.(4)
一个球的体积是36π,它的表面积是________.答案:(1)
(2)
16π(3)
(4)
36π8.两个半径为1的铁球,熔化成一个大球,这个大球的半径是________.解析:设大球半径为R,则πR3=π×13+π×13,∴R3=2,R=.答案:9.球的半径扩大为原来的2倍,它的体积扩大为原来的________
倍.解析:设球原来半径为R,则扩大后半径为2R,V球原=πR3,V球扩=π(2R)3=8V球原.答案:810.将一钢球放入底面半径为3
cm的圆柱形玻璃容器中,水面升高4
cm,则钢球的半径是________.解析:圆柱形玻璃容器中水面升高4
cm,则钢球的体积为V=π×32×4=36π,即有πR3=36π,∴R=3.答案:3
cm11.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1、2、3,则此球的表面积为________.答案:14π12.球面上有四个点P,A,B,C,如果PA,PB,PC两两互相垂直,且PA=PB=PC=a,求这个球的表面积.解析:PA,PB,PC两两互相垂直,将三棱锥补成一个以P为顶点的正方体,且PA=PB=PC=a,∴正方体的对角线长就是球的直径,∴2R=a,R=a,∴这个球的表面积为S球=4πR2=4π2=3πa2.13.把直径分别为6
cm,8
cm,10
cm的三个铜球熔制成一个较大的铜球,再把球削成一个棱长最长的正方体,求此正方体的体积.解析:设熔制后的大铜球半径为r,则π(33+43+53)=πr3,∴r=6
cm.据题意:此正方体为球的内接正方体,球的直径即为正方体对角线的长,故正方体的棱长a===4
cm.∴V正方体=a3=(4)3=192
cm3.14.如图所示,一个容器的盖子用一个正四棱台和一个球焊接而成,球的半径为R,正四棱台的上、下底面边长分别为2.5R和3R,斜高为0.6R.(1)求这个容器盖子的表面积(用R表示,焊接处对面积的影响忽略不计);解析:由题意,知S正四棱台=4××(2.5R+3R)×0.6R+(2.5R)2+(3R)2=21.85R2,S球=4πR2,所以这个盖子的表面积为S表=(21.85+4π)R2,(2)若R=2
cm,为盖子涂色时所用的涂料每0.4
kg可以涂1
m2,计算为100个这样的盖子涂色用涂料多少千克(精确到0.1
kg).解析:取R=2,π=3.14,得S表=137.64(cm2).100个这样的盖子共需涂料约为(137.64×100)÷10
000×0.4≈0.6
kg.
PAGE
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
