新人教A版高中数学必修第二册:直线方程
文档属性
| 名称 | 新人教A版高中数学必修第二册:直线方程 |
|
|
| 格式 | zip | ||
| 文件大小 | 625.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 20:34:42 | ||
图片预览





文档简介
授课主题
直线方程
教学目标
1.会由直线的一点坐标与斜率求直线的方程,掌握直线点斜式方程的形式.2.了解斜截式方程y=kx+b是点斜式方程的特殊形式.3.会根据直线的点斜式方程求直线的截距.4.掌握直线方程的两点式、截距式以及它们之间的联系和转化,并能根据条件熟练地求出满足已知条件的直线方程.5.体会直线的点斜式、斜截式、两点式和截距式表示直线有一定的局限性,只有直线的一般式能表示所有的直线.6.清楚直线与二元一次方程的对应关系,能由直线的一般式转化为所需要的其他直线形式.
教学内容
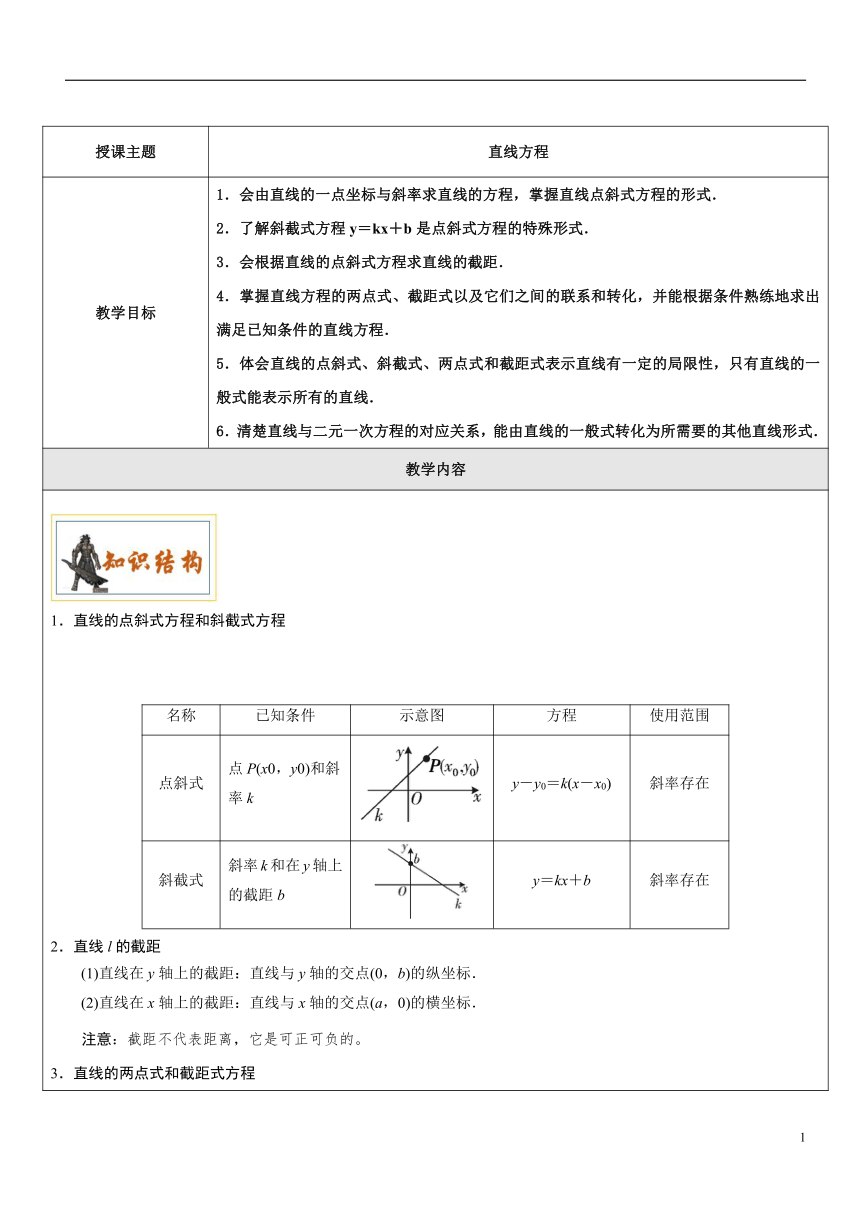
直线的点斜式方程和斜截式方程名称已知条件示意图方程使用范围点斜式点P(x0,y0)和斜率ky-y0=k(x-x0)斜率存在斜截式斜率k和在y轴上的截距by=kx+b斜率存在2.直线l的截距(1)直线在y轴上的截距:直线与y轴的交点(0,b)的纵坐标.(2)直线在x轴上的截距:直线与x轴的交点(a,0)的横坐标.
注意:截距不代表距离,它是可正可负的。3.直线的两点式和截距式方程名称已知条件示意图方程使用范围两点式P1(x1,y1),P2(x2,y2),其中x1≠x2,y1≠y2=斜率存在且不为0截距式在x,y轴上的截距分别为a,b且ab≠0+=1斜率存在且不为0,不过原点4.两点式的几种变化(1)
=(x1≠x2,y1≠y2).
该式不能替代两点式,因为此方程中x-x1≠0,会比原来方程表示的直线少一点.(2)
(y-y1)(x2-x1)=(x-x1)(y2-y1).
该式可以替代两点式,且可表示任意两点P1(x1,y1),P2(x2,y2)所在直线的方程。5.直线的一般式方程(1)在平面直角坐标系中,任何一条直线都可以用以下关于x,y的方程表示:(、不全为零)(2)每个关于x,y的二元一次方程都表示一条直线.题型一 求直线的点斜式方程例1 你能写出下列直线的点斜式方程吗?(1)经过点A(2,5),斜率是4;(2)经过点B(2,3),倾斜角是45°;(3)经过点C(-1,-1),与x轴平行;(4)经过点D(1,1),与x轴垂直.解析:(1)y-5=4(x-2);(2)∵k=tan
45°=1,∴y-3=x-2;(3)y=-1;(4)x=1.点评:(1)利用直线的点斜式求直线方程须满足两个条件:即一点P(x0,y0)和斜率k.(2)过点P(x0,y0)的直线有无数条,但可以分成两类:①斜率存在的直线,可写成点斜式y-y0=k(x-x0);②斜率不存在的直线,不能写成点斜式,方程为x=x0.巩
固 写出下列直线的点斜式方程.(1)斜率是3,经过点(0,-3);(2)倾斜角是60°,经过点(1,2);(3)倾斜角是150°,经过点(0,0).解析:(1)y+3=3x(2)∵k=tan
60°=,∴y-2=(x-1)(3)∵k=tan
150°=-,∴y=-x.题型二 求直线的斜截式方程例2
写出下列直线的斜截式方程.(1)斜率是3,在y轴上的截距是-3;(2)倾斜角是60°,在y轴上的截距是5;(3)倾斜角是150°,在y轴上的截距是0.解析:(1)y=3x-3.(2)∵k=tan
60°=,∴直线方程为y=x+5.(3)∵k=tan
150°=-,∴直线方程为y=-x.点评:直线在y轴上的截距是直线与y轴交点的纵坐标,可以是负数、零、正数.巩
固 写出斜率为2,在y轴上截距为m的直线方程,当m为何值时,直线通过点(1,1).解析:由直线方程的斜截式,得直线方程为y=2x+m.∵直线通过点(1,1),将x=1,y=1代入方程y=2x+m得1=2×1+m,∴m=-1.题型三 利用平行与垂直条件求直线的方程例3 (1)求经过点(1,1),且与直线y=2x+7平行的直线方程;(2)求经过点(0,2),且与x轴平行的直线方程;(3)求经过点(-1,1),且与直线y=-2x+7垂直的直线方程;(4)求经过点(-2,-2),且与x轴垂直的直线方程.解析:(1)由y=2x+7得k1=2,由两直线平行知k2=k1=2,∴所求直线方程为y-1=2(x-1).(2)∵所求直线与x轴平行,∴斜率为0.又过(0,2)点,∴所求直线方程为y=2.(3)由y=-2x+7得k1=-2,由两直线垂直知k1k2=-1,∴k2=12,∴所求直线方程为y-1=12(x+1).(4)∵所求直线与x轴垂直,∴斜率不存在.又过(-2,-2)点,∴所求直线方程为x=-2.点评:利用已知条件,寻求所求直线的斜率以及经过的一点,从而写出直线方程.巩
固 已知直线l1的方程为y=-2x+3,l2的方程为y=4x-2,直线l与l1平行且与l2在y轴上的截距相同,求直线l的方程.解析:由题意,直线l的斜率为k=-2,且在y轴上的截距为-2,故l的方程为y=-2x-2.题型四 两直线位置关系的综合应用例4 求斜率为且与两坐标轴围成的三角形周长为12的直线方程.解析:设直线方程为y=x+b,令x=0,得y=b.令y=0,得x=-b.∴|b|++=12.∴|b|+|b|+|b|=12,∴b=±3.∴所求方程为y=x±3.点评:解此题时要注意b为截距,“截距”不是距离,故解题时距离为截距的绝对值.巩
固 (1)当a为何值时,直线l1:y=-x+2a与直线l2:y=(a2-2)x+2平行.(2)当a为何值时,直线l1:y=(2a-1)x+3与直线l2:y=4x-3垂直.解析:(1)由题意可得,k1=-1,k2=a2-2,因为l1∥l2,所以解得a=-1,所以当a=-1时,直线l1∥l2.(2)由题意可得,k1=2a-1,k2=4,因为l1⊥l2,所以4(2a-1)=-1,解得a=,所以当a=时,直线l1⊥l2.点评:两条直线的斜率均存在时,若l1∥l2,则k1=k2且b1≠b2,若l1⊥l2则k1k2=-1.要注意当两条直线斜率均不存在时,仍然有l1∥l2;若一条直线的斜率不存在,一条直线的斜率为0,则有l1⊥l2.在解决有关两直线的位置关系的题目时一定要注意直线斜率的存在与否.题型五 求直线的两点式方程例5 三角形的顶点A(-5,0),B(3,-3),C(0,2),求这个三角形三边所在直线的方程.解析:利用两点式求解,但要注意隐含条件.∵直线AB过点A(-5,0),B(3,-3),∴由两点式得=.化简整理得3x+8y+15=0,这就是直线AB的方程.同理可得直线BC的方程5x+3y-6=0,直线AC的方程为2x-5y+10=0.点评:(1)已知不垂直两轴的直线上的两点,便可以利用直线的两点式方程求其方程,也可以先求斜率,再用点斜式求其方程.(2)当直线斜率不存在或斜率为0时,都不能用两点式来求它的方程(易错点).(3)两点式方程完全可以不记,可转化为两点定斜率、点斜式写方程;当斜率不存在时,直线方程为x=x1.巩
固 △ABC的顶点坐标分别是A(-3,0),B(9,5),C(3,9),求△ABC的中线AD所在直线的方程.解析:线段BC的中点D的坐标是(6,7),由两点式方程得直线AD的方程=,即7x-9y+21=0.题型六 求直线的截距式方程例6
直线l过点(-3,4),且在两坐标轴上的截距之和为12,求直线l的方程.解析:由于直线在两坐标轴上的截距之和为12,因此直线l在两轴上的截距都存在且不过原点,故可设为截距式直线方程.设直线l的方程为+=1,则a+b=12.①又直线l过点(-3,4),∴+=1.②由①②解得或故所求的直线方程为+=1或+=1,即x+3y-9=0或4x-y+16=0.点评:(1)如果问题中涉及直线与坐标轴相交,则可考虑选用截距式直线方程,用待定系数法确定其系数即可.(2)选用截距式直线方程时,首先必须考虑直线能否过原点以及能否与两坐标轴垂直.(3)要注意截距式直线方程的逆向运用,如由方程+=1可知该直线在x轴和y轴上的截距分别为3和-2.巩
固 一条直线经过点A(-2,2),并且与两坐标轴围成的三角形的面积为1,求此直线方程.解析:设所求直线方程为+=1,∵点A(-2,2)在直线上,故有-+=1.①又因直线与坐标轴围成的三角形面积为1,∴|a||b|=1.②由①,②可得或解得或所求的直线方程为+=1或+=1.即x+2y-2=0或2x+y+2=0为所求.巩
固 求过点(3,-2),且在两坐标轴上的截距相等的直线方程.解析:对于该题,容易产生如下的错误解法:错解一:由于直线l的截距相等,故直线l的斜率为±1.若k=1,则直线方程为y+2=x-3,即为x-y-5=0;若k=-1,则直线方程为y+2=-(x-3),即为x+y-1=0.错解二:由题意直线在两坐标轴上的截距相等,可设直线的方程为+=1,由于直线过点(3,-2),则有+=1,所以a=1,即所求的直线方程为x+y-1=0.在上述两种错解中,错解一忽视了截距的意义,截距不是距离,它可正可负,也可以为0.当k=1时,直线x-y-5=0在两轴上的截距分别为5和-5,它们是不相等的.另外,这种解法还漏掉了直线在两轴上的截距均为0的特殊情形.错解二中,没有注意到截距式方程的适用范围,同样也产生了漏解.正解:设直线l在两坐标轴上的截距均为a,(1)若a=0,则直线l过原点,满足题设条件.此时l的方程为2x+3y=0;(2)若a≠0,则l的方程可设为+=1.因为l过点(3,-2),所以+=1,即a=1.所以直线l的方程为x+y=1,即x+y-1=0.综上所述:直线l的方程为2x+3y=0,或x+y-1=0.题型七 一般式与其他形式的互化例7 根据下列条件分别写出直线的方程,并化为一般式方程.(1)斜率是,且经过点A(5,3);(2)斜率为4,在y轴上的截距为-2;(3)经过A(-1,5),B(2,-1)两点;(4)在x,y轴上的截距分别是-3,-1.解析:(1)由点斜式方程可知,所求直线方程为:y-3=(x-5),化为一般式为:x-y+3-5=0.(2)由斜截式方程可知,所求直线方程为:y=4x-2,化为一般式为:4x-y-2=0.(3)由两点式方程可知,所求直线方程为:=.化为一般式方程为:2x+y-3=0.(4)由截距式方程可得,所求直线方程为+=1,化成一般式方程为:x+3y+3=0.点评:这类题目求解的关键是选准合适的方程形式,对于一般式方程,x的系数一般为非负数且x,y的系数不要有分数.巩
固 已知直线l经过点A(-5,6)和点B(-4,8),求直线的一般式方程和截距式方程.解析:直线过A(-5,6)、B(-4,8)两点,由两点式得,=,整理得
2x-y+16=0,∴2x-y=-16,两边同时除以-16,得+=1.故所求直线的一般式方程为2x-y+16=0,截距式方程为+=1.题型八 用直线方程的一般式研究平行与垂直关系例8
a为何值时,直线(a-1)x-2y+4=0与x-ay-1=0,(1)平行;(2)垂直?解析:当a=0或1时,两直线既不平行,也不垂直;当a≠0且a≠1时,直线(a-1)x-2y+4=0的斜率为k1=,截距为b1=2;直线x-ay-1=0的斜率为k2=,截距为b2=-.(1)由k1=k2,b1≠b2,即=,a≠-,解得a=-1或a=2.所以当a=-1或2时,两直线平行.(2)由k1·k2=-1,即·=-1,解得a=.所以当a=时,两直线垂直.点评:按有无斜率及斜率是否为0进行讨论,也可按平行或垂直的充要条件来解.巩
固 已知点A(2,2)和直线l:3x+4y-20=0,求:(1)过点A和直线l平行的直线方程;(2)过点A和直线l垂直的直线方程.解析:解法一:(1)由题意,所求直线斜率为-,过点A(2,2),则所求方程为y-2=-(x-2),即3x+4y-14=0.(2)由题意,所求直线斜率为,过点A(2,2),则所求直线方程为y-2=(x-2),即4x-3y-2=0.解法二:(1)由题意,设所求直线方程为3x+4y+c=0,将点A(2,2)代入得c=-14,则所求直线方程为3x+4y-14=0.(2)由题意,设所求直线方程为4x-3y+c=0,将点A(2,2)代入,得c=-2,则所求直线的方程为4x-3y-2=0.题型九 含参数的直线问题例9 若直线(m+1)x+(m2-m-2)y=m+1在y轴上截距等于1,求实数m的值解析:①当m+1=0即m=-1时,方程不表示直线,∴m≠-1.②直线方程化为截距式得:+=1,由=1解得:m=-1或m=3.∵m≠-1,综上所述,m=3.点评:利用直线的点斜式,斜截式,两点式、截距式求解直线的方程时,一定要注意每种方程形式的适用范围,要注意对斜率是否存在,截距是否为0进行分类讨论,最后将方程形式转化为一般式.巩
固 设直线l的方程为(m2-2m-3)x+(2m2+m-1)y=2m-6,根据下列条件分别确定实数m的值.(1)l在x轴上的截距为-3;(2)斜率为1.解析:(1)令y=0,依题意得由①得m≠3且m≠-1,由②得3m2-4m-15=0,解得m=3或m=-.综上所述,m=-.(2)由题意得由③得m≠-1且m≠,解④得m=-1或.∴m=.1.经过点(-3,2),倾斜角为60°的直线方程是( )A.y+2=(x-3)
B.y-2=(x+3)C.y-2=(x+3)
D.y+2=(x-3)答案:C2.如下图所示,方程y=ax+表示的直线可能是( )答案:B3.已知直线l1:y=kx+b,l2:y=bx+k,则它们的图象可能为( )答案:C4.经过原点,且倾斜角是直线y=x+1倾斜角2倍的直线是( )A.x=0
B.y=0C.y=x
D.y=2x答案:D5.欲使直线(m+2)x-y-3=0与直线(3m-2)x-y+1=0平行,则实数m的值是( )A.1
B.2C.3
D.不存在解析:把直线化为斜截式,得出斜率,通过直线平行的条件计算.答案:B6.直线y=k(x-2)+3必过定点,该定点为( )A.(3,2)
B.(2,3)C.(2,-3)
D.(-2,3)解析:直线方程改写为y-3=k(x-2),则过定点(2,3).答案:B7.若直线(m+2)x+(m2-2m-3)y=2m在x轴上的截距是3,则m的值是( )A.
B.6
C.-
D.-6解析:令y=0,得(m+2)x=2m,将x=3代入得m=-6,故选D.答案:D8.过P1(2,0),P2(0,3)两点的直线方程是( )A.+=1
B.+=1C.-=1
D.-=1答案:B9.直线-=1在y轴上的截距为( )A.|b|
B.±b
C.b2
D.-b2答案:D10.下列四个命题中是真命题的是( )A.经过定点P0(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示B.经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线都可以用方程(y-y1)·(x2-x1)=(x-x1)·(y2-y1)表示C.不经过原点的直线都可以用方程+=1表示D.经过定点A(0,b)的直线都可以用方程y=kx+b表示答案:B11.直线ax+by=1(a,b≠0)与两坐标轴围成的三角形的面积是( )A.ab
B.|ab|
C.
D.解析:直线ax+by=1可化为+=1,故其围成的三角形的面积为S=
=.答案:D12.过点A(-1,2)作直线l,使它在x轴、y轴上的截距相等,则这样的直线有( )A.4条
B.3条
C.2条
D.1条解析:分截距为0和不为0的两种情况讨论,各有一条直线.答案:C13.过点A(1,2)且在两坐标轴上截距的绝对值相等的直线的条数为( )A.1条
B.2条
C.3条
D.4条解析:分截距为0,截距不为0且相等或互为相反数,共三种情况.答案:C14.直线y-1=4(x+2)化为一般式方程为( )A.4(x+2)-y+1=0
B.y=4x+9C.4x-y+9=0
D.=4答案:C15.过点(-1,3)且垂直于直线x-2y+3=0的直线方程为( )A.2x+y-1=0
B.2x+y-5=0C.x+2y-5=0
D.x-2y+7=0答案:A16.直线l1:x+ay+6=0与l2:(a-2)x+3y+2a=0平行,则a的值等于( )A.-1或3
B.1或3
C.-3
D.-1解析:由题意,两直线斜率存在,由l1∥l2知=≠,∴a=-1答案:D17.直线3x-2y-4=0的截距式方程是( )A.-=1
B.-=4C.+=1
D.+=1答案:D18.已知点A(1,2),B(3,1),则线段AB的垂直平分线的方程是( )A.4x+2y=5
B.4x-2y=5C.x+2y=5
D.x-2y=5解析:kAB==-,由k·kAB=-1得k=2.由中点坐标公式得x==2,y==,∴中点坐标为.由点斜式方程得y-=2(x-2),即4x-2y=5.答案:B19.直线(a+2)x+(1-a)y-3=0与(a-1)x+(2a+3)y+2=0互相垂直,则a=( )A.-1
B.1
C.±1
D.-解析:由(a+2)(a-1)+(1-a)(2a+3)=0化简得1-a2=0,∴a=±1.答案:C20.直线l的方程为Ax+By+C=0,若直线l过原点和二、四象限,则( )A.C=0,B>0
B.A>0,B>0,C=0C.AB<0,C=0
D.AB>0,C=0答案:D21.纵截距为-4,与两坐标轴围成三角形的面积为20的直线的一般式方程为________________.解析:由题意,设所求直线为+=1,且|4a|=20,∴|a|=10即a=10或-10,则其方程为-=1或-=1,可化为2x-5y-20=0或2x+5y+20=0.答案:2x-5y-20=0或2x+5y+20=022.若三角形ABC的顶点A(-5,0),B(3,-2),C(1,2),则经过AB、BC两边中点的直线方程为________.答案:x-3y-2=023.过点C(-4,0),D(0,-6)的直线的截距式方程是__________,化为斜截式方程是__________.答案:+=1 y=-x-624.已知直线x+y+3=0,则直线的斜率为__________,在x轴上的截距为________,在y轴上的截距为________.答案:-1 -3 -325.求倾斜角为直线y=-x+1的倾斜角的一半,且分别满足下列条件的直线方程:(1)经过点(-4,1);(2)在y轴上的截距为-10.解析:∵直线l1:y=-x+1的斜率k1=-,∴直线的倾斜角为120°,由题意知,所求直线的倾斜角为60°,斜率k=.(1)∵过点(-4,1),∴直线方程为y-1=(x+4).(2)∵在y轴上截距为-10,∴直线方程为y=x-10.26.已知直线l在y轴上的截距为-3,且它与两坐标轴围成的三角形的面积为6.求直线l的方程.解析:由已知得直线l的斜率存在且不等于零.设直线l的方程为y=kx-3.当y=0时,x=,∴××3=6.解得
k=±,∴所求直线方程为
y=±x-3.27.已知直线l在x轴上的截距比在y轴上的截距大1,且过定点(6,-2),求直线l的方程.解析:解法一:设直线l的点斜式方程为y+2=k(x-6)(k≠0).令x=0,得y=-6k-2;令y=0,得x=+6.∴-(-6k-2)=1,解得:k1=-或k2=-.∴直线l的方程为y+2=-(x-6)或y+2=-(x-6).即y=-x+2或y=-x+1.解法二:设直线的斜截式方程为y=kx+b.令y=0,则x=-.依题意得:?或∴直线l的方程为y=-x+1或y=-x+2.解法三:设直线l与y轴的交点为(0,b),则直线方程的两点式为=.令y=0,得x=.∴=1+b,解得b1=1或b2=2.∴直线l的方程为x+2y-2=0或2x+3y-6=0.解法四:设直线方程的截距式为+=1,又直线l过点(6,-2).∴+=1,解得b1=1,b2=2.∴直线l的方程为+y=1或+=1.即x+2y-2=0或2x+3y-6=0.28.(1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值.解析:解法一:由l1:2x+(m+1)y+4=0.l2:mx+3y-2=0.①当m=0时,显然l1与l2不平行.②当m≠0时,l1∥l2,需=≠.解得m=2或m=-3.∴m的值为2或-3.解法二:令2×3=m(m+1),解得m=-3或m=2.当m=-3时,l1:x-y+2=0,l2:3x-3y+2=0,显然l1与l2不重合,∴l1∥l2.同理当m=2时,l1:2x+3y+4=0,l2:2x+3y-2=0,l1与l2不重合,l1∥l2,∴m的值为2或-3.(2)直线的截距式方程+=1化为斜截式方程为y=-2x+b,化为一般式方程为bx+ay-8=0.求a,b的值.解析:由+=1,化得y=-x+b=-2x+b,又可化得:bx+ay-ab=bx+ay-8=0,则=2,且ab=8.解得a=2,b=4或a=-2,b=-4.29.(1)已知三直线l1:2x-4y+7=0,l2:x-2y+5=0,l3:4x+2y-1=0,求证:l1∥l2,l1⊥l3;(1)证明:把l1、l2、l3的方程写成斜截式得l1:y=x+;l2:y=x+;l3:y=-2x+,∵k1=k2=,b1=≠=b2,∴l1∥l2.∵k3=-2,∴k1·k3=-1,∴l1⊥l3.(2)求过点A(2,2)且分别满足下列条件的直线方程:①与直线2x+y-1=0平行;②与2x+y-1=0垂直.(2)解法一:已知直线l:2x+y-1=0的斜率k=-2.①过A(2,2)与l平行的直线方程为y-2=-2(x-2).即2x+y-6=0.②过A与l垂直的直线的斜率k1=-=,方程为y-2=(x-2).即x-2y+2=0为所求.解法二:①设所求直线方程为2x+y+c=0,由(2,2)点在直线上,∴2×2+2+c=0,∴c=-6.∴所求直线为2x+y-6=0.②设所求直线方程为x-2y+λ=0,由(2,2)点在直线上,∴2-2×2+λ=0,∴λ=2.∴所求直线为x-2y+2=0.1.直线的方程y-y0=k(x-x0)( )A.可以表示任何直线B.不能表示过原点的直线C.不能表示与y轴垂直的直线D.不能表示与x轴垂直的直线答案:D2.直线3x+2y+6=0的斜率为k,在y轴上的截距为b,则有( )A.k=-,b=3
B.k=-,b=-2C.k=-,b=-3
D.k=-,b=-3答案:C3.直线y=ax+b(a+b=0,ab≠0)的图象可能是下列图中的( )答案:D4.过两点(6,2),(3,2)的直线方程是( )A.x=5
B.y=2
C.x+y=2
D.x=2答案:B5.在x,y轴上的截距分别是-3,4的直线方程是( )A.+=1
B.+=1C.-=1
D.+=1答案:A6.一条直线不与坐标轴平行或重合,则它的方程( )A.可以写成两点式或截距式B.可以写成两点式或斜截式或点斜式C.可以写成点斜式或截距式D.可以写成两点式或截距式或斜截式或点斜式答案:B7.若方程Ax+By+C=0表示直线,则A,B应满足的条件是( )A.A≠0
B.B≠0C.A·B≠0
D.A2+B2≠0答案:D8.在同一坐标系中,直线l1:ax-y+b=0与l2:bx+y-a=0(ab≠0)只可能是( )解析:根据l1的位置确定a,b的正负,从而再确定l2的位置.答案:D9.若AC<0,BC<0,则直线Ax+By+C=0不通过( )A.第一象限
B.第二象限C.第三象限
D.第四象限解析:将直线化为斜截式方程为y=-x-,又AC<0,BC<0,∴AB>0,故-<0,->0.答案:C10.直线+=1,化成一般式方程为( )A.y=-x+4
B.y=-(x-3)C.4x+3y-12=0
D.4x+3y=12答案:C11.已知直线l1过点P(2,1)且与直线l2:y=x+1垂直,则l1的点斜式方程为_________.答案:y-1=-(x-2)12.已知△ABC的三个顶点A(1,3),B(5,7),C(10,12),则BC边上的高所在直线的方程为解析:由kBC==1知所求直线斜率为-1.答案:y=-x+413.填空:(1)两点式直线方程不能表示与__________平行的直线.(2)截距式中a表示在________的截距,b表示在________的截距,它们均可正可负.(3)直线+=1在x轴上截距为:______,y轴上截距为:________.答案:(1)
x轴或y轴
(2)x轴上 y轴上 (3)-3 2.14.若直线l的方程为2x-y=-1,则它的截距式方程为________,斜截式方程为________,直线l与x轴交于点________,与y轴交于点________.答案:+=1 y=6x+3 (0,3)15.过点A(3,-1),B(5,4)的直线方程的两点式为________,化成一般式为________,化为截距式为________,斜截式为________.答案:= ;
5x-2y-17=0;
+=1; y=x-.
PAGE
直线方程
教学目标
1.会由直线的一点坐标与斜率求直线的方程,掌握直线点斜式方程的形式.2.了解斜截式方程y=kx+b是点斜式方程的特殊形式.3.会根据直线的点斜式方程求直线的截距.4.掌握直线方程的两点式、截距式以及它们之间的联系和转化,并能根据条件熟练地求出满足已知条件的直线方程.5.体会直线的点斜式、斜截式、两点式和截距式表示直线有一定的局限性,只有直线的一般式能表示所有的直线.6.清楚直线与二元一次方程的对应关系,能由直线的一般式转化为所需要的其他直线形式.
教学内容
直线的点斜式方程和斜截式方程名称已知条件示意图方程使用范围点斜式点P(x0,y0)和斜率ky-y0=k(x-x0)斜率存在斜截式斜率k和在y轴上的截距by=kx+b斜率存在2.直线l的截距(1)直线在y轴上的截距:直线与y轴的交点(0,b)的纵坐标.(2)直线在x轴上的截距:直线与x轴的交点(a,0)的横坐标.
注意:截距不代表距离,它是可正可负的。3.直线的两点式和截距式方程名称已知条件示意图方程使用范围两点式P1(x1,y1),P2(x2,y2),其中x1≠x2,y1≠y2=斜率存在且不为0截距式在x,y轴上的截距分别为a,b且ab≠0+=1斜率存在且不为0,不过原点4.两点式的几种变化(1)
=(x1≠x2,y1≠y2).
该式不能替代两点式,因为此方程中x-x1≠0,会比原来方程表示的直线少一点.(2)
(y-y1)(x2-x1)=(x-x1)(y2-y1).
该式可以替代两点式,且可表示任意两点P1(x1,y1),P2(x2,y2)所在直线的方程。5.直线的一般式方程(1)在平面直角坐标系中,任何一条直线都可以用以下关于x,y的方程表示:(、不全为零)(2)每个关于x,y的二元一次方程都表示一条直线.题型一 求直线的点斜式方程例1 你能写出下列直线的点斜式方程吗?(1)经过点A(2,5),斜率是4;(2)经过点B(2,3),倾斜角是45°;(3)经过点C(-1,-1),与x轴平行;(4)经过点D(1,1),与x轴垂直.解析:(1)y-5=4(x-2);(2)∵k=tan
45°=1,∴y-3=x-2;(3)y=-1;(4)x=1.点评:(1)利用直线的点斜式求直线方程须满足两个条件:即一点P(x0,y0)和斜率k.(2)过点P(x0,y0)的直线有无数条,但可以分成两类:①斜率存在的直线,可写成点斜式y-y0=k(x-x0);②斜率不存在的直线,不能写成点斜式,方程为x=x0.巩
固 写出下列直线的点斜式方程.(1)斜率是3,经过点(0,-3);(2)倾斜角是60°,经过点(1,2);(3)倾斜角是150°,经过点(0,0).解析:(1)y+3=3x(2)∵k=tan
60°=,∴y-2=(x-1)(3)∵k=tan
150°=-,∴y=-x.题型二 求直线的斜截式方程例2
写出下列直线的斜截式方程.(1)斜率是3,在y轴上的截距是-3;(2)倾斜角是60°,在y轴上的截距是5;(3)倾斜角是150°,在y轴上的截距是0.解析:(1)y=3x-3.(2)∵k=tan
60°=,∴直线方程为y=x+5.(3)∵k=tan
150°=-,∴直线方程为y=-x.点评:直线在y轴上的截距是直线与y轴交点的纵坐标,可以是负数、零、正数.巩
固 写出斜率为2,在y轴上截距为m的直线方程,当m为何值时,直线通过点(1,1).解析:由直线方程的斜截式,得直线方程为y=2x+m.∵直线通过点(1,1),将x=1,y=1代入方程y=2x+m得1=2×1+m,∴m=-1.题型三 利用平行与垂直条件求直线的方程例3 (1)求经过点(1,1),且与直线y=2x+7平行的直线方程;(2)求经过点(0,2),且与x轴平行的直线方程;(3)求经过点(-1,1),且与直线y=-2x+7垂直的直线方程;(4)求经过点(-2,-2),且与x轴垂直的直线方程.解析:(1)由y=2x+7得k1=2,由两直线平行知k2=k1=2,∴所求直线方程为y-1=2(x-1).(2)∵所求直线与x轴平行,∴斜率为0.又过(0,2)点,∴所求直线方程为y=2.(3)由y=-2x+7得k1=-2,由两直线垂直知k1k2=-1,∴k2=12,∴所求直线方程为y-1=12(x+1).(4)∵所求直线与x轴垂直,∴斜率不存在.又过(-2,-2)点,∴所求直线方程为x=-2.点评:利用已知条件,寻求所求直线的斜率以及经过的一点,从而写出直线方程.巩
固 已知直线l1的方程为y=-2x+3,l2的方程为y=4x-2,直线l与l1平行且与l2在y轴上的截距相同,求直线l的方程.解析:由题意,直线l的斜率为k=-2,且在y轴上的截距为-2,故l的方程为y=-2x-2.题型四 两直线位置关系的综合应用例4 求斜率为且与两坐标轴围成的三角形周长为12的直线方程.解析:设直线方程为y=x+b,令x=0,得y=b.令y=0,得x=-b.∴|b|++=12.∴|b|+|b|+|b|=12,∴b=±3.∴所求方程为y=x±3.点评:解此题时要注意b为截距,“截距”不是距离,故解题时距离为截距的绝对值.巩
固 (1)当a为何值时,直线l1:y=-x+2a与直线l2:y=(a2-2)x+2平行.(2)当a为何值时,直线l1:y=(2a-1)x+3与直线l2:y=4x-3垂直.解析:(1)由题意可得,k1=-1,k2=a2-2,因为l1∥l2,所以解得a=-1,所以当a=-1时,直线l1∥l2.(2)由题意可得,k1=2a-1,k2=4,因为l1⊥l2,所以4(2a-1)=-1,解得a=,所以当a=时,直线l1⊥l2.点评:两条直线的斜率均存在时,若l1∥l2,则k1=k2且b1≠b2,若l1⊥l2则k1k2=-1.要注意当两条直线斜率均不存在时,仍然有l1∥l2;若一条直线的斜率不存在,一条直线的斜率为0,则有l1⊥l2.在解决有关两直线的位置关系的题目时一定要注意直线斜率的存在与否.题型五 求直线的两点式方程例5 三角形的顶点A(-5,0),B(3,-3),C(0,2),求这个三角形三边所在直线的方程.解析:利用两点式求解,但要注意隐含条件.∵直线AB过点A(-5,0),B(3,-3),∴由两点式得=.化简整理得3x+8y+15=0,这就是直线AB的方程.同理可得直线BC的方程5x+3y-6=0,直线AC的方程为2x-5y+10=0.点评:(1)已知不垂直两轴的直线上的两点,便可以利用直线的两点式方程求其方程,也可以先求斜率,再用点斜式求其方程.(2)当直线斜率不存在或斜率为0时,都不能用两点式来求它的方程(易错点).(3)两点式方程完全可以不记,可转化为两点定斜率、点斜式写方程;当斜率不存在时,直线方程为x=x1.巩
固 △ABC的顶点坐标分别是A(-3,0),B(9,5),C(3,9),求△ABC的中线AD所在直线的方程.解析:线段BC的中点D的坐标是(6,7),由两点式方程得直线AD的方程=,即7x-9y+21=0.题型六 求直线的截距式方程例6
直线l过点(-3,4),且在两坐标轴上的截距之和为12,求直线l的方程.解析:由于直线在两坐标轴上的截距之和为12,因此直线l在两轴上的截距都存在且不过原点,故可设为截距式直线方程.设直线l的方程为+=1,则a+b=12.①又直线l过点(-3,4),∴+=1.②由①②解得或故所求的直线方程为+=1或+=1,即x+3y-9=0或4x-y+16=0.点评:(1)如果问题中涉及直线与坐标轴相交,则可考虑选用截距式直线方程,用待定系数法确定其系数即可.(2)选用截距式直线方程时,首先必须考虑直线能否过原点以及能否与两坐标轴垂直.(3)要注意截距式直线方程的逆向运用,如由方程+=1可知该直线在x轴和y轴上的截距分别为3和-2.巩
固 一条直线经过点A(-2,2),并且与两坐标轴围成的三角形的面积为1,求此直线方程.解析:设所求直线方程为+=1,∵点A(-2,2)在直线上,故有-+=1.①又因直线与坐标轴围成的三角形面积为1,∴|a||b|=1.②由①,②可得或解得或所求的直线方程为+=1或+=1.即x+2y-2=0或2x+y+2=0为所求.巩
固 求过点(3,-2),且在两坐标轴上的截距相等的直线方程.解析:对于该题,容易产生如下的错误解法:错解一:由于直线l的截距相等,故直线l的斜率为±1.若k=1,则直线方程为y+2=x-3,即为x-y-5=0;若k=-1,则直线方程为y+2=-(x-3),即为x+y-1=0.错解二:由题意直线在两坐标轴上的截距相等,可设直线的方程为+=1,由于直线过点(3,-2),则有+=1,所以a=1,即所求的直线方程为x+y-1=0.在上述两种错解中,错解一忽视了截距的意义,截距不是距离,它可正可负,也可以为0.当k=1时,直线x-y-5=0在两轴上的截距分别为5和-5,它们是不相等的.另外,这种解法还漏掉了直线在两轴上的截距均为0的特殊情形.错解二中,没有注意到截距式方程的适用范围,同样也产生了漏解.正解:设直线l在两坐标轴上的截距均为a,(1)若a=0,则直线l过原点,满足题设条件.此时l的方程为2x+3y=0;(2)若a≠0,则l的方程可设为+=1.因为l过点(3,-2),所以+=1,即a=1.所以直线l的方程为x+y=1,即x+y-1=0.综上所述:直线l的方程为2x+3y=0,或x+y-1=0.题型七 一般式与其他形式的互化例7 根据下列条件分别写出直线的方程,并化为一般式方程.(1)斜率是,且经过点A(5,3);(2)斜率为4,在y轴上的截距为-2;(3)经过A(-1,5),B(2,-1)两点;(4)在x,y轴上的截距分别是-3,-1.解析:(1)由点斜式方程可知,所求直线方程为:y-3=(x-5),化为一般式为:x-y+3-5=0.(2)由斜截式方程可知,所求直线方程为:y=4x-2,化为一般式为:4x-y-2=0.(3)由两点式方程可知,所求直线方程为:=.化为一般式方程为:2x+y-3=0.(4)由截距式方程可得,所求直线方程为+=1,化成一般式方程为:x+3y+3=0.点评:这类题目求解的关键是选准合适的方程形式,对于一般式方程,x的系数一般为非负数且x,y的系数不要有分数.巩
固 已知直线l经过点A(-5,6)和点B(-4,8),求直线的一般式方程和截距式方程.解析:直线过A(-5,6)、B(-4,8)两点,由两点式得,=,整理得
2x-y+16=0,∴2x-y=-16,两边同时除以-16,得+=1.故所求直线的一般式方程为2x-y+16=0,截距式方程为+=1.题型八 用直线方程的一般式研究平行与垂直关系例8
a为何值时,直线(a-1)x-2y+4=0与x-ay-1=0,(1)平行;(2)垂直?解析:当a=0或1时,两直线既不平行,也不垂直;当a≠0且a≠1时,直线(a-1)x-2y+4=0的斜率为k1=,截距为b1=2;直线x-ay-1=0的斜率为k2=,截距为b2=-.(1)由k1=k2,b1≠b2,即=,a≠-,解得a=-1或a=2.所以当a=-1或2时,两直线平行.(2)由k1·k2=-1,即·=-1,解得a=.所以当a=时,两直线垂直.点评:按有无斜率及斜率是否为0进行讨论,也可按平行或垂直的充要条件来解.巩
固 已知点A(2,2)和直线l:3x+4y-20=0,求:(1)过点A和直线l平行的直线方程;(2)过点A和直线l垂直的直线方程.解析:解法一:(1)由题意,所求直线斜率为-,过点A(2,2),则所求方程为y-2=-(x-2),即3x+4y-14=0.(2)由题意,所求直线斜率为,过点A(2,2),则所求直线方程为y-2=(x-2),即4x-3y-2=0.解法二:(1)由题意,设所求直线方程为3x+4y+c=0,将点A(2,2)代入得c=-14,则所求直线方程为3x+4y-14=0.(2)由题意,设所求直线方程为4x-3y+c=0,将点A(2,2)代入,得c=-2,则所求直线的方程为4x-3y-2=0.题型九 含参数的直线问题例9 若直线(m+1)x+(m2-m-2)y=m+1在y轴上截距等于1,求实数m的值解析:①当m+1=0即m=-1时,方程不表示直线,∴m≠-1.②直线方程化为截距式得:+=1,由=1解得:m=-1或m=3.∵m≠-1,综上所述,m=3.点评:利用直线的点斜式,斜截式,两点式、截距式求解直线的方程时,一定要注意每种方程形式的适用范围,要注意对斜率是否存在,截距是否为0进行分类讨论,最后将方程形式转化为一般式.巩
固 设直线l的方程为(m2-2m-3)x+(2m2+m-1)y=2m-6,根据下列条件分别确定实数m的值.(1)l在x轴上的截距为-3;(2)斜率为1.解析:(1)令y=0,依题意得由①得m≠3且m≠-1,由②得3m2-4m-15=0,解得m=3或m=-.综上所述,m=-.(2)由题意得由③得m≠-1且m≠,解④得m=-1或.∴m=.1.经过点(-3,2),倾斜角为60°的直线方程是( )A.y+2=(x-3)
B.y-2=(x+3)C.y-2=(x+3)
D.y+2=(x-3)答案:C2.如下图所示,方程y=ax+表示的直线可能是( )答案:B3.已知直线l1:y=kx+b,l2:y=bx+k,则它们的图象可能为( )答案:C4.经过原点,且倾斜角是直线y=x+1倾斜角2倍的直线是( )A.x=0
B.y=0C.y=x
D.y=2x答案:D5.欲使直线(m+2)x-y-3=0与直线(3m-2)x-y+1=0平行,则实数m的值是( )A.1
B.2C.3
D.不存在解析:把直线化为斜截式,得出斜率,通过直线平行的条件计算.答案:B6.直线y=k(x-2)+3必过定点,该定点为( )A.(3,2)
B.(2,3)C.(2,-3)
D.(-2,3)解析:直线方程改写为y-3=k(x-2),则过定点(2,3).答案:B7.若直线(m+2)x+(m2-2m-3)y=2m在x轴上的截距是3,则m的值是( )A.
B.6
C.-
D.-6解析:令y=0,得(m+2)x=2m,将x=3代入得m=-6,故选D.答案:D8.过P1(2,0),P2(0,3)两点的直线方程是( )A.+=1
B.+=1C.-=1
D.-=1答案:B9.直线-=1在y轴上的截距为( )A.|b|
B.±b
C.b2
D.-b2答案:D10.下列四个命题中是真命题的是( )A.经过定点P0(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示B.经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线都可以用方程(y-y1)·(x2-x1)=(x-x1)·(y2-y1)表示C.不经过原点的直线都可以用方程+=1表示D.经过定点A(0,b)的直线都可以用方程y=kx+b表示答案:B11.直线ax+by=1(a,b≠0)与两坐标轴围成的三角形的面积是( )A.ab
B.|ab|
C.
D.解析:直线ax+by=1可化为+=1,故其围成的三角形的面积为S=
=.答案:D12.过点A(-1,2)作直线l,使它在x轴、y轴上的截距相等,则这样的直线有( )A.4条
B.3条
C.2条
D.1条解析:分截距为0和不为0的两种情况讨论,各有一条直线.答案:C13.过点A(1,2)且在两坐标轴上截距的绝对值相等的直线的条数为( )A.1条
B.2条
C.3条
D.4条解析:分截距为0,截距不为0且相等或互为相反数,共三种情况.答案:C14.直线y-1=4(x+2)化为一般式方程为( )A.4(x+2)-y+1=0
B.y=4x+9C.4x-y+9=0
D.=4答案:C15.过点(-1,3)且垂直于直线x-2y+3=0的直线方程为( )A.2x+y-1=0
B.2x+y-5=0C.x+2y-5=0
D.x-2y+7=0答案:A16.直线l1:x+ay+6=0与l2:(a-2)x+3y+2a=0平行,则a的值等于( )A.-1或3
B.1或3
C.-3
D.-1解析:由题意,两直线斜率存在,由l1∥l2知=≠,∴a=-1答案:D17.直线3x-2y-4=0的截距式方程是( )A.-=1
B.-=4C.+=1
D.+=1答案:D18.已知点A(1,2),B(3,1),则线段AB的垂直平分线的方程是( )A.4x+2y=5
B.4x-2y=5C.x+2y=5
D.x-2y=5解析:kAB==-,由k·kAB=-1得k=2.由中点坐标公式得x==2,y==,∴中点坐标为.由点斜式方程得y-=2(x-2),即4x-2y=5.答案:B19.直线(a+2)x+(1-a)y-3=0与(a-1)x+(2a+3)y+2=0互相垂直,则a=( )A.-1
B.1
C.±1
D.-解析:由(a+2)(a-1)+(1-a)(2a+3)=0化简得1-a2=0,∴a=±1.答案:C20.直线l的方程为Ax+By+C=0,若直线l过原点和二、四象限,则( )A.C=0,B>0
B.A>0,B>0,C=0C.AB<0,C=0
D.AB>0,C=0答案:D21.纵截距为-4,与两坐标轴围成三角形的面积为20的直线的一般式方程为________________.解析:由题意,设所求直线为+=1,且|4a|=20,∴|a|=10即a=10或-10,则其方程为-=1或-=1,可化为2x-5y-20=0或2x+5y+20=0.答案:2x-5y-20=0或2x+5y+20=022.若三角形ABC的顶点A(-5,0),B(3,-2),C(1,2),则经过AB、BC两边中点的直线方程为________.答案:x-3y-2=023.过点C(-4,0),D(0,-6)的直线的截距式方程是__________,化为斜截式方程是__________.答案:+=1 y=-x-624.已知直线x+y+3=0,则直线的斜率为__________,在x轴上的截距为________,在y轴上的截距为________.答案:-1 -3 -325.求倾斜角为直线y=-x+1的倾斜角的一半,且分别满足下列条件的直线方程:(1)经过点(-4,1);(2)在y轴上的截距为-10.解析:∵直线l1:y=-x+1的斜率k1=-,∴直线的倾斜角为120°,由题意知,所求直线的倾斜角为60°,斜率k=.(1)∵过点(-4,1),∴直线方程为y-1=(x+4).(2)∵在y轴上截距为-10,∴直线方程为y=x-10.26.已知直线l在y轴上的截距为-3,且它与两坐标轴围成的三角形的面积为6.求直线l的方程.解析:由已知得直线l的斜率存在且不等于零.设直线l的方程为y=kx-3.当y=0时,x=,∴××3=6.解得
k=±,∴所求直线方程为
y=±x-3.27.已知直线l在x轴上的截距比在y轴上的截距大1,且过定点(6,-2),求直线l的方程.解析:解法一:设直线l的点斜式方程为y+2=k(x-6)(k≠0).令x=0,得y=-6k-2;令y=0,得x=+6.∴-(-6k-2)=1,解得:k1=-或k2=-.∴直线l的方程为y+2=-(x-6)或y+2=-(x-6).即y=-x+2或y=-x+1.解法二:设直线的斜截式方程为y=kx+b.令y=0,则x=-.依题意得:?或∴直线l的方程为y=-x+1或y=-x+2.解法三:设直线l与y轴的交点为(0,b),则直线方程的两点式为=.令y=0,得x=.∴=1+b,解得b1=1或b2=2.∴直线l的方程为x+2y-2=0或2x+3y-6=0.解法四:设直线方程的截距式为+=1,又直线l过点(6,-2).∴+=1,解得b1=1,b2=2.∴直线l的方程为+y=1或+=1.即x+2y-2=0或2x+3y-6=0.28.(1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值.解析:解法一:由l1:2x+(m+1)y+4=0.l2:mx+3y-2=0.①当m=0时,显然l1与l2不平行.②当m≠0时,l1∥l2,需=≠.解得m=2或m=-3.∴m的值为2或-3.解法二:令2×3=m(m+1),解得m=-3或m=2.当m=-3时,l1:x-y+2=0,l2:3x-3y+2=0,显然l1与l2不重合,∴l1∥l2.同理当m=2时,l1:2x+3y+4=0,l2:2x+3y-2=0,l1与l2不重合,l1∥l2,∴m的值为2或-3.(2)直线的截距式方程+=1化为斜截式方程为y=-2x+b,化为一般式方程为bx+ay-8=0.求a,b的值.解析:由+=1,化得y=-x+b=-2x+b,又可化得:bx+ay-ab=bx+ay-8=0,则=2,且ab=8.解得a=2,b=4或a=-2,b=-4.29.(1)已知三直线l1:2x-4y+7=0,l2:x-2y+5=0,l3:4x+2y-1=0,求证:l1∥l2,l1⊥l3;(1)证明:把l1、l2、l3的方程写成斜截式得l1:y=x+;l2:y=x+;l3:y=-2x+,∵k1=k2=,b1=≠=b2,∴l1∥l2.∵k3=-2,∴k1·k3=-1,∴l1⊥l3.(2)求过点A(2,2)且分别满足下列条件的直线方程:①与直线2x+y-1=0平行;②与2x+y-1=0垂直.(2)解法一:已知直线l:2x+y-1=0的斜率k=-2.①过A(2,2)与l平行的直线方程为y-2=-2(x-2).即2x+y-6=0.②过A与l垂直的直线的斜率k1=-=,方程为y-2=(x-2).即x-2y+2=0为所求.解法二:①设所求直线方程为2x+y+c=0,由(2,2)点在直线上,∴2×2+2+c=0,∴c=-6.∴所求直线为2x+y-6=0.②设所求直线方程为x-2y+λ=0,由(2,2)点在直线上,∴2-2×2+λ=0,∴λ=2.∴所求直线为x-2y+2=0.1.直线的方程y-y0=k(x-x0)( )A.可以表示任何直线B.不能表示过原点的直线C.不能表示与y轴垂直的直线D.不能表示与x轴垂直的直线答案:D2.直线3x+2y+6=0的斜率为k,在y轴上的截距为b,则有( )A.k=-,b=3
B.k=-,b=-2C.k=-,b=-3
D.k=-,b=-3答案:C3.直线y=ax+b(a+b=0,ab≠0)的图象可能是下列图中的( )答案:D4.过两点(6,2),(3,2)的直线方程是( )A.x=5
B.y=2
C.x+y=2
D.x=2答案:B5.在x,y轴上的截距分别是-3,4的直线方程是( )A.+=1
B.+=1C.-=1
D.+=1答案:A6.一条直线不与坐标轴平行或重合,则它的方程( )A.可以写成两点式或截距式B.可以写成两点式或斜截式或点斜式C.可以写成点斜式或截距式D.可以写成两点式或截距式或斜截式或点斜式答案:B7.若方程Ax+By+C=0表示直线,则A,B应满足的条件是( )A.A≠0
B.B≠0C.A·B≠0
D.A2+B2≠0答案:D8.在同一坐标系中,直线l1:ax-y+b=0与l2:bx+y-a=0(ab≠0)只可能是( )解析:根据l1的位置确定a,b的正负,从而再确定l2的位置.答案:D9.若AC<0,BC<0,则直线Ax+By+C=0不通过( )A.第一象限
B.第二象限C.第三象限
D.第四象限解析:将直线化为斜截式方程为y=-x-,又AC<0,BC<0,∴AB>0,故-<0,->0.答案:C10.直线+=1,化成一般式方程为( )A.y=-x+4
B.y=-(x-3)C.4x+3y-12=0
D.4x+3y=12答案:C11.已知直线l1过点P(2,1)且与直线l2:y=x+1垂直,则l1的点斜式方程为_________.答案:y-1=-(x-2)12.已知△ABC的三个顶点A(1,3),B(5,7),C(10,12),则BC边上的高所在直线的方程为解析:由kBC==1知所求直线斜率为-1.答案:y=-x+413.填空:(1)两点式直线方程不能表示与__________平行的直线.(2)截距式中a表示在________的截距,b表示在________的截距,它们均可正可负.(3)直线+=1在x轴上截距为:______,y轴上截距为:________.答案:(1)
x轴或y轴
(2)x轴上 y轴上 (3)-3 2.14.若直线l的方程为2x-y=-1,则它的截距式方程为________,斜截式方程为________,直线l与x轴交于点________,与y轴交于点________.答案:+=1 y=6x+3 (0,3)15.过点A(3,-1),B(5,4)的直线方程的两点式为________,化成一般式为________,化为截距式为________,斜截式为________.答案:= ;
5x-2y-17=0;
+=1; y=x-.
PAGE
