新人教A版高中数学必修第二册:线性回归
文档属性
| 名称 | 新人教A版高中数学必修第二册:线性回归 |

|
|
| 格式 | zip | ||
| 文件大小 | 818.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 00:00:00 | ||
图片预览




文档简介
授课主题
线性回归及应用
教学目标
1.通过典型案例的探究,进一步了解回归分析的基本思想、方法及初步应用.2.通过实例进一步了解与非线性回归模型有关的统计思想.3.了解判断刻画模型拟合效果的方法——相关指数和残差分析.
教学内容
线性回归模型(1)函数关系是一种确定性关系,而相关关系是一种非确定性关系.(2)回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.(3)对于一组具有线性相关关系的数据(x1,y1),(x2,y2),…,(xn,yn),回归直线的斜率和截距的最小二乘估计公式分别为=
=
,
=-
,其中(,)称为样本点的中心.(4)线性回归模型y=bx+a+e,其中a和b是模型的未知参数,e称为随机误差,自变量x称为解释变量,因变量y称为预报变量.把和称为未知参数a和b的最好估计.相关系数相关系数:r=
.当r>0时,两个变量正相关;当r<0时,两个变量负相关.相关系数的绝对值越接近于1,两个变量的线性相关关系越强,它们的散点图越接近一条直线,这时用线性回归模型拟合这组数据就越好.此时建立的线性回归模型是有意义的.残差的概念对于样本点(x1,y1),(x2,y2),…,(xn,yn)而言,它们的随机误差为ei=yi-bxi-a,i=1,2,…,n,其估计值为
i=yi-i=yi-
xi-,i=1,2,…,n,
i称为相应于点(xi,yi)的残差.总偏差平方和、残差平方和、回归平方和、相关指数:名称总偏差平方和残差平方和回归平方和说明所有单个样本值与样本均值差的平方和回归值与样本值差的平方和总偏差平方和-残差平方和公式(yi-)2(yi-i)2(yi-)2-(yi-i)2相关指数R2=1-.刻画回归效果的方式(1)残差图法作图时纵坐标为残差,横坐标可以选为的样本编号,或身高数据,或体重的估计值等,这样作出的图形称为残差图.在残差图中,残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适,这样的带状区域的宽度越窄,说明模型拟合精度越高.(2)残差平方和法残差平方和越小,模型拟合效果越好.(3)利用R2刻画回归效果R2表示解释变量对于预报变量变化的贡献率.R2越接近于1,表示回归的效果越好.建立回归模型的基本步骤(1)确定研究对象,明确哪个变量是解释变量,哪个变量是预报变量.(2)画出确定好的解释变量和预报变量的散点图,观察它们之间的关系.(3)确定回归方程的类型.(4)按一定规则估计回归方程中的参数.(5)分析残差图是否有异常.残差分析(1)残差:样本值与回归值的差叫做残差,即e=yi-i.(2)残差分析:通过残差来判断模型拟合的效果,判断原始数据中是否存在可疑数据,这方面的分析工作称为残差分析.(3)残差图:以残差为纵坐标,以样本编号或身高数据或体重估计值等为横坐标,作出的图形称为残差图.观察残差图,如果残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适,这样的带状区域的宽度越窄,模型拟合精度越高,回归方程的预报精度越高.一般情况下,比较两个模型的残差比较困难(某些样本点上一个模型的残差的绝对值比另一个模型的小,而另一些样本点的情况则相反),故通过比较两个模型的残差的平方和的大小来判断模型的拟合效果.残差平方和越小的模型,拟合的效果越好.题型一 线性回归分析例1 某种产品的广告费用支出x与销售额y(单位:百万元)之间有如下的对应数据:x/百万元24568y/百万元3040605070(1)画出散点图;(2)求回归直线方程;(3)试预测广告费用支出为10百万元时,销售额多大?解析:(1)散点图如图所示:(2)列出下表,并用科学计算器进行有关计算:i12345合计xi2456825yi3040605070250xiyi601603003005601
380x416253664145所以,==5,==50,=145,iyi=1
380.于是可得===6.5,=-eq
\o(x,\s\up6(-))=50-6.5×5=17.5.所以所求的线性回归方程为=6.5x+17.5.(3)根据上面求得的线性回归方程,当广告费用支出为10百万元时,=6.5×10+17.5=82.5(百万元),即广告费用支出为10百万元时,销售额大约为82.5百万元.点评:(1)散点图是定义在具有相关关系的两个变量的基础上的,对于性质不明确的两组数据,可先画散点图,在图形上看它们是否有关系,以及关系的密切程度,然后再进行回归分析;(2)求回归方程,只有散点图大致呈线性时求出的回归方程才有实际意义,否则,求出的回归方程没有意义.求线性回归方程的步骤:①列表表示xi,yi,xiyi;②计算,,,iyi;③代入公式计算,的值;④写出线性回归方程.巩
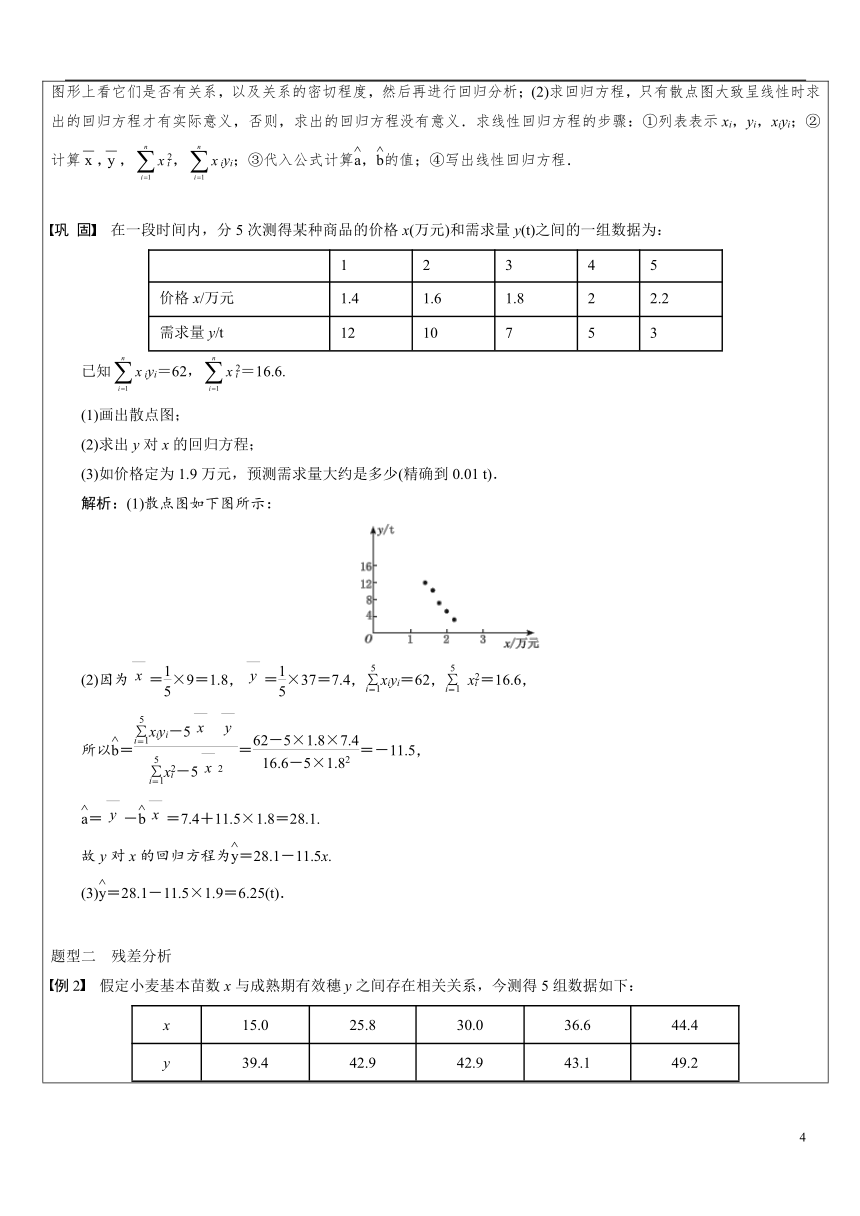
固 在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:12345价格x/万元1.41.61.822.2需求量y/t1210753已知iyi=62,=16.6.(1)画出散点图;(2)求出y对x的回归方程;(3)如价格定为1.9万元,预测需求量大约是多少(精确到0.01
t).解析:(1)散点图如下图所示:(2)因为=×9=1.8,=×37=7.4,xiyi=62,
x=16.6,所以=eq
\f(\o(∑,\s\up6(5),\s\do4(i=1))xiyi-5\x\to(x)
\x\to(y),\o(∑,\s\up6(5),\s\do4(i=1))x-5\x\to(x)2)==-11.5,=-eq
\x\to(x)=7.4+11.5×1.8=28.1.故y对x的回归方程为=28.1-11.5x.(3)=28.1-11.5×1.9=6.25(t).题型二 残差分析例2 假定小麦基本苗数x与成熟期有效穗y之间存在相关关系,今测得5组数据如下:x15.025.830.036.644.4y39.442.942.943.149.2(1)以x为解释变量,y为预报变量,作出散点图;(2)求y与x之间的回归方程,并对于基本苗数56.7预报有效穗;(3)计算各组残差,并计算残差平方和;(4)求相关指数R2,并说明残差变量对有效穗的影响占百分之几.解析:(1)散点图如下:(2)由图看出,样本点呈条状分布,有比较好的线性相关关系,因此可以用线性回归方程刻画它们之间的关系.设回归方程为y=x+,=30.36,=43.5.=5
101.56,iyi=6
746.76.所以=
eq
\f(\o(∑,\s\up6(5),\s\do4(i=1))xiyi-5\x\to(x)
\x\to(y),\o(∑,\s\up6(5),\s\do4(i=1))x-5\x\to(x)2)≈0.29,=-eq
\x\to(x)≈34.67.故所求的回归直线方程为=34.67+0.29x.当x=56.7时,=34.67+0.29×56.7=51.113.估计成熟期有效穗为51.113.(3)由于y=bx+a+e,可以算出i=yi-i,
分别为1=0.38,2=0.748,3=-0.47,4=-2.184,5=1.654.残差平方和:
eq
\o\al(2,i)≈8.43.(4)
(yi-)2=50.18,∴R2=1-≈0.832.所以解释变量小麦基本苗数对总效应约贡献了83.2%.残差变量贡献了约1-83.2%=16.8%.点评:要熟悉刻画回归效果的三种方式(1)残差图法:残差点比较均匀地落在水平的带状区域内说明选用的模型比较合适.(2)残差平方和法:残差平方和(yi-)2越小,模型的拟合效果越好.(3)R2法:R2=1-越接近1,表明回归的效果越好.巩
固 甲、乙、丙、丁4位同学各自对A,B两变量进行回归分析,分别得到散点图与残差平方和(yi-i)2如表所示:甲乙丙丁散点图残差平方和115106124103哪位同学的试验结果体现拟合A,B两变量关系的模型拟合精度高( )A.甲
B.乙
C.丙
D.丁解析:根据线性相关的知识,散点图中各样本点条状分布越均匀,同时保持残差平方和越小(对于已经获取的样本数据,R2的表达式中(yi-i)2为确定的数,则残差平方和越小,R2越大),由回归分析建立的线性回归模型的拟合效果越好,由试验结果知丁要好些.故选D.答案:D题型三
非线性回归分析例3 某地区不同身高的未成年男性的体重平均值如下表:身高x/cm60708090100110体重y/kg6.137.909.9912.1515.0217.50身高x/cm120130140150160170体重y/kg20.9226.8631.1138.8547.2555.05试建立y与x之间的回归方程.解析:根据上表中的数据画出散点图(如下图所示):由图看出,样本点分布在某条指数函数曲线的周围,于是令z=ln
y.x60708090100110z1.812.072.302.502.712.86x120130140150160170z3.043.293.443.663.864.01画出散点图(如下图所示):由表中数据可得z与x之间的回归直线方程:=0.693+0.020x,则有=e0.693+0.020x.点评:三种常见的非线性回归模型的处理方法:①指数函数型y=ebx+a,两边取对数得ln
y=ln
ebx+a,即ln
y=bx+a,令z=ln
y,把原始数据(x,y)转化为(x,z),再根据线性回归模型的方法求出a,b.②对数函数型y=bln
x+a,设x′=ln
x,原方程可化为y=bx′+a,再根据线性回归模型的方法求出a,b.③二次函数型y=bx2+a,设x′=x2,原方程可化为y=bx′+a,再根据线性回归模型的方法求出a,b.巩
固 若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,由例3中求出的回归方程,那么这个地区一名身高为175
cm,体重为82
kg的在校男生体重是否正常?解析:当x=175时,预测平均体重=e0.693+0.020×175≈66.22,由于66.22×1.2≈79.46<82,所以这个男生偏胖.题型四 线性回归分析的应用例4 以下是某地搜集到的新房屋的销售价格y(万元)和房屋的面积x(m2)的数据房屋面积x/m211511080135105销售价格y/万元24.821.618.429.222(1)画出数据对应的散点图;(2)求线性回归方程,
并在散点图中加上回归直线;(3)据(2)的结果估计当房屋面积为150
m2时的销售价格.解析:(1)数据对应的散点图如图所示:(2)=i=109,
lxy=(xi-)2=1
570,=23.2,lxx=(xi-)(
yi-)=308.设所求回归直线方程为=x+,则==≈0.196
2,=-
=1.816
6.故所求回归直线方程为=0.196
2x+1.816
6.(3)据(2),当x=150
m2时,销售价格的估计值为=0.196
2×150+1.816
6=31.246
6(万元).点评:已知x与y呈线性相关关系,就无需进行相关性检验,否则要进行相关性检验.如果两个变量不具备相关关系,或者相关关系不显著,即使求出回归方程也是毫无意义的,用其估计和预测也是不可信的.进行线性相关的判断,可通过散点图直观判断,散点图不明显的可进行相关性检验.巩
固 某农场对单位面积化肥用量x(kg)和水稻相应产量y(kg)的关系作了统计,得到数据如下:x15202530354045y330345365405445450455如果x与y之间具有线性相关关系,求出回归直线方程,并预测当单位面积化肥用量为32
kg时水稻的产量大约是多少(精确到0.01
kg).解析:(1)
列表如下:序号xyx2xy1153302254
9502203454006
9003253656259
12543040590012
1505354451
22515
5756404501
60018
0007454552
02520
475∑2102
7957
00087
175=×210=30,=×2
795≈399.3,=≈4.746,=399.3-4.746×30=256.92.y对x的回归直线方程为=256.92+4.746x.当x=32时,=256.92+4.746×32≈408.79.即回归直线方程为=256.92+4.746x.当单位面积化肥用量为32
kg时,水稻的产量约为408.79
kg.题型五 相关分析项例5 某同学6次考试的数学、语文成绩在班中的排名如下表:数学名次x765321语文名次y13119642对上述数据分别用=x+与=x2+来拟合y与x之间的关系,并用残差分析两者的拟合效果.解析:首先用=x+来拟合y与x之间的关系.因为=4,=7.5,(xi-)(yi-)=50,(xi-)2=28,所以==≈1.786,=-eq
\o(x,\s\up6(-))=0.356.所以=1.786x+0.356,此时的残差平方和为(yi-i)2≈0.214.再用=x2+来拟合y与x之间的关系.令t=x2,则对应表中数据为t493625941y13119642因为=20.667,=7.5,(ti-)(yi-)=400,(ti-)2≈1
857.333,所以==≈0.215,=-eq
\o(t,\s\up6(-))≈3.057.所以=0.215x+3.057,此时的残差平方和为(yi-i)2≈3.355.因为3.355>0.214,所以用=x+来拟合y与x之间的关系效果较好.点评:(1)残差平方和越小,预报精确度越高.(2)相关指数R2取得越大,说明模型的拟合效果越好.
巩
固 已知某校5个学生的数学和物理成绩如下:学生的编号12345数学成绩x8075706560物理成绩y7066686462(1)通过大量事实证明发现,一个学生的数学成绩和物理成绩是具有很强的线性相关关系的,在上述表格中,用x表示数学成绩,用y表示物理成绩,求y关于x的回归方程.(2)利用残差分析回归方程的拟合效果,若残差和在(-0.1,0.1)范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.解析:(1)由已知数据得,=70,=66,
代入公式,可求得=0.36,=40.8,故回归直线方程为=0.36x+40.8.(2)由=0.36x+40.8可知1=0.36×80+40.8=69.6,同理可得2=67.8,3=66,4=64.2,5=62.4,所以(yi-i)=0∈(-0.1,0.1),故该回归方程是“优拟方程”.(线性回归)A组1.下列变量具有相关关系的是( )A.人的身高与视力B.角的大小与所对的圆弧长C.直线上某点的横坐标与纵坐标D.人的年龄与身高答案:D2.在对两个变量x、y进行线性回归分析时一般有下列步骤:
①对所求出的回归方程作出解释;②收集数据(xi,yi),i=1,2,…,n;③求线性回归方程;④求相关系数;⑤根据所搜集的数据绘制散点图.如果根据可靠性要求能够判定变量x,y具有线性相关性,则在下列操作顺序中正确的是( )A.①②⑤③④
B.③②④⑤①C.②④③①⑤
D.②⑤④③①答案:D3.下列关于线性回归的判断,正确的个数是( )①若散点图中的所有点都在一条直线附近,则这条直线为回归直线;②散点图中的绝大多数点都线性相关,个别特殊点不影响线性回归,如图中的A,B,C点;③已知回归直线方程为=0.50x-0.81,则x=25时,y的估计值为11.69;④线性回归方程的意义是它反映了样本整体的变化趋势.A.0个
B.1个
C.2个
D.3个解析:因为由最小二乘法求得的回归方程直线才是真正的回归直线,所以①错;将x=25代入=0.50x-0.81得=11.69,所以③正确;根据回归方程的概念知②④也正确.故选D.答案:DB组一、选择题1.下列4个散点图中,不能用回归模型拟合的两个变量是( )解析:观察散点图可知,选项B中的点近似分布在一条抛物线附近,可以转化为线性回归模型;选项C、D中的点近似分布在一条直线附近,选项A中的点无规律.故选A.答案:A2.下表给出5组数据(x,y),为选出4组数据使线性相关程度最大,且保留第1组数据,则应去掉( )i12345xi-5-4-3-24yi-3-24-16A.第2组
B.第3组
C.
第4组
D.
第5组解析:作出散点图,可知,去掉第3组(-3,4)后的4组数据大致分布在一条直线附近.故选B.答案:B3.对于线性相关系数r,下列说法中正确的是( )A.|r|∈(-∞,+∞),|r|越大,相关程度越大;反之,相关程度越小B.|r|≤1,r越大,相关程度越大;反之,相关程度越小C.|r|≤1,且|r|越接近于1,相关程度越大;|r|越接近于0,相差程度越小D.以上说法都不正确答案:C4.工人月工资y(元)关于劳动生产率x(千元)的回归方程为=650+80x,下列说法中正确的个数是( )①劳动生产率为1
000元时,工资为730元;②劳动生产率提高1
000元时,则工资提高80元;③劳动生产率提高1
000元时,则工资提高730元;④当月工资为810元时,劳动生产率约为2
000元.A.1个
B.2个
C.3个
D.4个答案:C5.某产品的广告费用x(万元)与销售额y(万元)的统计数据如下表:广告费用x/万元4235销售额y/万元49263954根据上表可得回归方程=x+中的为9.4,据此模型预报广告费用为6万元时销售额为( )A.63.6万元
B.65.5万元
C.67.7万元
D.72.0万元解析:由表可计算==,==42,因为点在回归直线=x+上,且为9.4,所以42=9.4×+,
解得=9.1,故回归方程为=9.4x+9.1,
令x=6,得=65.5(万元),选B.答案:B二、填空题6.已知关于两个变量x、y
的回归方程为=1.5x+45,x∈{1,5,7,13,19},则=__________.解析:易知=9,因为=1.5+45,所以=1.5+45=1.5×9+45=58.5.答案:58.57.若对于变量y与x的10组统计数据的回归模型中,R2=0.95,又知残差平方和为120.53,那么(yi-)2的值为________________.解析:依题意有0.95=1-,所以(yi-)2=2
410.6.答案:2
410.68.某数学老师身高176
cm,他爷爷、父亲和儿子的身高分别是173
cm,170
cm和182
cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________cm.答案:185三、解答题9.在10年期间,一城市居民年收入与某种商品的销售额之间的关系见下表:第几年城市居民年收入x/亿元某商品的销售额y/万元132.225.0231.130.0332.934.0435.837.0537.139.0638.041.0739.042.0843.044.0944.648.01046.051.0(1)画出散点图;(2)如果散点图中各点大致分布在一条直线的附近,求y与x之间的线性回归方程;(3)试预测居民年收入50亿元时这种商品的销售额.解析:(1)散点图如下图所示:(2)观察散点图可知各点大致分布在一条直线的附近.列表,利用计算器进行计算:序号xiyixyxiyi132.225.01
036.84625805231.130.0967.21900933332.934.01
082.411
1561
118.6435.837.01
281.641
3691
324.6537.139.01
376.411
5211
446.9638.041.01
4441
6811
558739.042.01
5211
7641
638843.044.01
8491
9361
892944.648.01
989.162
3042
140.81046.051.02
1162
6012
346∑379.739114
663.6715
85715
202.9==≈1.447,=-=39.1-1.447×37.97≈-15.84,故所求线性回归方程为=1.447x-15.84.(3)根据上面求得的线性回归方程,当居民年收入50亿元时,=1.447×50-15.84=56.51(万元),即这种商品销售额大约为56.51万元.10.为了研究三月下旬的平均气温x(℃)与四月二十号前棉花害虫化蛹高峰日y的关系,某地区观察了2007年至2012年的情况,得到下面的数据:年份200720082009201020112012x/℃24.429.632.928.730.328.9y19611018据气象台预测,该地区在2013年三月下旬平均气温为27
℃,试估计2013年四月化蛹高峰日为哪天.解析:画出x与y的散点图可知,x与y有线性相关关系(图略).=i=29.13,=i=7.5,=5
130.92,iyi=1
222.6,∴==-2.2,=-=7.5-(-2.2)×29.13=71.6.∴回归直线方程为=-2.2x+71.6.当x=27时,=-2.2×27+71.6=12.2.据此,可估计该地区2013年4月12日或13日为化蛹高峰日.
A组1.有下列说法:①线性回归分析就是由样本点去寻找一条直线贴近这些样本点的数学方法;②利用样本点的散点图可以直观判断两个变量是否具有线性关系;③通过回归方程=x+及其回归系数,可以估计变量的取值和变化趋势;④因为由任何一组观测值都可以求得一个回归直线方程,所以没有必要进行相关性检验.其中正确命题的个数是( )A.1个
B.2个
C.3个
D.4个答案:C2.有下列说法:①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;②用相关指数R2来刻画回归的效果,R2值越大,说明模型的拟合效果越好;③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型,拟合效果越好.其中正确命题的个数是( )A.0个
B.1个
C.2个
D.3个答案:D3.某考察团对全国10个城市进行职工人均工资水平x(千元)与居民人均消费水平y(千元)统计调查,y与x具有相关关系,回归方程为=0.66x+1.562.若某城市居民人均消费水平为7.675(千元),估计该城市人均消费额占人均工资收入的百分比约为( )A.83%
B.72%
C.67%
D.66%解析:由已知=7.675,代入方程=0.66x+1.562,得x≈9.262
1,所以百分比为=83%.故选A.答案:AB组一、选择题1.
下面两个变量间的关系不是函数关系的是( )A.正方形的棱长与体积B.角的度数与它的余弦值C.
单产量为常数时,土地面积与粮食总产量D.日照时间与水稻亩产量解析:选项D为相关关系,其余均为函数关系.故选D.答案:D2.可用来分析身高与体重有关系的是( )A.残差分析
B.回归分析
C.等高条形图
D.独立检验解析:因为身高与体重是两个具有相关关系的变量,所以要用回归分析来解决.故选B.答案:B3.已知x,y取值如下表:x014568y1.31.85.66.17.49.3从所得的散点图分析可知:y与x线性相关,且=0.95x+a,则a=( )A.1.30
B.1.45
C.1.65
D.1.80解析:易得=4,=5.25,因线性回归方程通过样本点中心(,),故有5.25=0.95×4+a,所以a=1.45.故选B.答案:B4.四名同学根据各自的样本数据研究变量x、y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:①y与x负相关且=2.347x-6.423;②y与x负相关且=-3.476x+5.648;③y与x正相关且=5.437x+8.493;④y与x正相关且=-4.326x-4.578.其中一定不正确的结论的序号是( )A.①②
B.②③
C.③④
D.①④解析:x的系数大于0为正相关,小于0为负相关.
故选D.答案:D5.已知两个变量x和y之间具有线性相关性,甲、乙两个同学各自独立地做了10次和15次试验,并且利用线性回归的方法求得回归直线分别为l1和l2.已知两个人在试验中发现对变量x的观测数据的平均数都为s,对变量y的观测数据的平均数都是t,则下列说法中正确的是( )A.l1与l2可能有交点(s,t)B.l1与l2相交,但交点一定不是(s,t)C.l1与l2必定平行D.l1与l2必定重合答案:A二、填空题6.若一组观测值(x1,
y1),(x2,y2),…,(xn,yn)之间满足yi=bxi+a+ei
(i=1,2,…,n),ei恒为0,则R2为________.答案:17.已知两个变量x和y线性相关,5次试验的观测数据如下:x100120140160180y4554627592那么变量y关于x的回归方程是____________.答案:=0.575x-14.98.若某地财政收入x与支出y满足线性回归方程=x++ε(单位:亿元),其中=0.8,=2,|ε|≤0.5,如果今年该地区财政收入10亿元,则年支出预计不会超过________________亿元.解析:将x=10代入线性回归方程,得=0.8×10+2+ε=10+ε,因为|ε|≤0.5,所以=10+ε≤10.5.答案:10.5三、解答题9.在试验中得到变量y与x的数据(见下表):x0.066
70.038
80.033
30.027
30.022
5y39.442.941.043.149.2由经验知,y与之间具有线性相关关系,试求y与x之间的回归曲线方程;
当x0=0.038时,预测y0的值.分析:通过换元转化为线性回归问题.解析:令u=,由题目所给数据可得下表所示的数据:序号uiyiuuiyi115.039.4225591225.842.9665.641
106.82330.041.09001
230436.643.11
339.561
577.46544.449.21
971.362
184.48合计151.8215.65
101.566
689.76计算得=0.29,=34.32.∴=34.32+0.29u.所求回归曲线方程为=34.32+.当x0=0.038时,y0=34.32+≈41.95.10.在一段时间内,某种商品的价格x(元)和需求量y(件)之间的一组数据为:价格x/元1416182022需求量y/件1210753求出y对x的回归直线方程,并说明拟合效果的好坏.解析:=×(14+16+18+20+22)=18,=(12+10+7+5+3)=7.4,=142+162+182+202+222=1
660,=122+102+72+52+32=327,iyi=14×12+16×10+18×7+20×5+22×3=620,所以=
==-=-1.15,所以=7.4+1.15×18=28.1,所以回归直线方程为=-1.15x+28.1,列出残差表为:yi-i00.3-0.4-0.10.2yi-4.62.6-0.4-2.4-4.4所以(yi-i)2=0.3,(yi-)2=53.2,R2=1-≈0.994,因而拟合效果较好.
PAGE
线性回归及应用
教学目标
1.通过典型案例的探究,进一步了解回归分析的基本思想、方法及初步应用.2.通过实例进一步了解与非线性回归模型有关的统计思想.3.了解判断刻画模型拟合效果的方法——相关指数和残差分析.
教学内容
线性回归模型(1)函数关系是一种确定性关系,而相关关系是一种非确定性关系.(2)回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.(3)对于一组具有线性相关关系的数据(x1,y1),(x2,y2),…,(xn,yn),回归直线的斜率和截距的最小二乘估计公式分别为=
=
,
=-
,其中(,)称为样本点的中心.(4)线性回归模型y=bx+a+e,其中a和b是模型的未知参数,e称为随机误差,自变量x称为解释变量,因变量y称为预报变量.把和称为未知参数a和b的最好估计.相关系数相关系数:r=
.当r>0时,两个变量正相关;当r<0时,两个变量负相关.相关系数的绝对值越接近于1,两个变量的线性相关关系越强,它们的散点图越接近一条直线,这时用线性回归模型拟合这组数据就越好.此时建立的线性回归模型是有意义的.残差的概念对于样本点(x1,y1),(x2,y2),…,(xn,yn)而言,它们的随机误差为ei=yi-bxi-a,i=1,2,…,n,其估计值为
i=yi-i=yi-
xi-,i=1,2,…,n,
i称为相应于点(xi,yi)的残差.总偏差平方和、残差平方和、回归平方和、相关指数:名称总偏差平方和残差平方和回归平方和说明所有单个样本值与样本均值差的平方和回归值与样本值差的平方和总偏差平方和-残差平方和公式(yi-)2(yi-i)2(yi-)2-(yi-i)2相关指数R2=1-.刻画回归效果的方式(1)残差图法作图时纵坐标为残差,横坐标可以选为的样本编号,或身高数据,或体重的估计值等,这样作出的图形称为残差图.在残差图中,残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适,这样的带状区域的宽度越窄,说明模型拟合精度越高.(2)残差平方和法残差平方和越小,模型拟合效果越好.(3)利用R2刻画回归效果R2表示解释变量对于预报变量变化的贡献率.R2越接近于1,表示回归的效果越好.建立回归模型的基本步骤(1)确定研究对象,明确哪个变量是解释变量,哪个变量是预报变量.(2)画出确定好的解释变量和预报变量的散点图,观察它们之间的关系.(3)确定回归方程的类型.(4)按一定规则估计回归方程中的参数.(5)分析残差图是否有异常.残差分析(1)残差:样本值与回归值的差叫做残差,即e=yi-i.(2)残差分析:通过残差来判断模型拟合的效果,判断原始数据中是否存在可疑数据,这方面的分析工作称为残差分析.(3)残差图:以残差为纵坐标,以样本编号或身高数据或体重估计值等为横坐标,作出的图形称为残差图.观察残差图,如果残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适,这样的带状区域的宽度越窄,模型拟合精度越高,回归方程的预报精度越高.一般情况下,比较两个模型的残差比较困难(某些样本点上一个模型的残差的绝对值比另一个模型的小,而另一些样本点的情况则相反),故通过比较两个模型的残差的平方和的大小来判断模型的拟合效果.残差平方和越小的模型,拟合的效果越好.题型一 线性回归分析例1 某种产品的广告费用支出x与销售额y(单位:百万元)之间有如下的对应数据:x/百万元24568y/百万元3040605070(1)画出散点图;(2)求回归直线方程;(3)试预测广告费用支出为10百万元时,销售额多大?解析:(1)散点图如图所示:(2)列出下表,并用科学计算器进行有关计算:i12345合计xi2456825yi3040605070250xiyi601603003005601
380x416253664145所以,==5,==50,=145,iyi=1
380.于是可得===6.5,=-eq
\o(x,\s\up6(-))=50-6.5×5=17.5.所以所求的线性回归方程为=6.5x+17.5.(3)根据上面求得的线性回归方程,当广告费用支出为10百万元时,=6.5×10+17.5=82.5(百万元),即广告费用支出为10百万元时,销售额大约为82.5百万元.点评:(1)散点图是定义在具有相关关系的两个变量的基础上的,对于性质不明确的两组数据,可先画散点图,在图形上看它们是否有关系,以及关系的密切程度,然后再进行回归分析;(2)求回归方程,只有散点图大致呈线性时求出的回归方程才有实际意义,否则,求出的回归方程没有意义.求线性回归方程的步骤:①列表表示xi,yi,xiyi;②计算,,,iyi;③代入公式计算,的值;④写出线性回归方程.巩
固 在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:12345价格x/万元1.41.61.822.2需求量y/t1210753已知iyi=62,=16.6.(1)画出散点图;(2)求出y对x的回归方程;(3)如价格定为1.9万元,预测需求量大约是多少(精确到0.01
t).解析:(1)散点图如下图所示:(2)因为=×9=1.8,=×37=7.4,xiyi=62,
x=16.6,所以=eq
\f(\o(∑,\s\up6(5),\s\do4(i=1))xiyi-5\x\to(x)
\x\to(y),\o(∑,\s\up6(5),\s\do4(i=1))x-5\x\to(x)2)==-11.5,=-eq
\x\to(x)=7.4+11.5×1.8=28.1.故y对x的回归方程为=28.1-11.5x.(3)=28.1-11.5×1.9=6.25(t).题型二 残差分析例2 假定小麦基本苗数x与成熟期有效穗y之间存在相关关系,今测得5组数据如下:x15.025.830.036.644.4y39.442.942.943.149.2(1)以x为解释变量,y为预报变量,作出散点图;(2)求y与x之间的回归方程,并对于基本苗数56.7预报有效穗;(3)计算各组残差,并计算残差平方和;(4)求相关指数R2,并说明残差变量对有效穗的影响占百分之几.解析:(1)散点图如下:(2)由图看出,样本点呈条状分布,有比较好的线性相关关系,因此可以用线性回归方程刻画它们之间的关系.设回归方程为y=x+,=30.36,=43.5.=5
101.56,iyi=6
746.76.所以=
eq
\f(\o(∑,\s\up6(5),\s\do4(i=1))xiyi-5\x\to(x)
\x\to(y),\o(∑,\s\up6(5),\s\do4(i=1))x-5\x\to(x)2)≈0.29,=-eq
\x\to(x)≈34.67.故所求的回归直线方程为=34.67+0.29x.当x=56.7时,=34.67+0.29×56.7=51.113.估计成熟期有效穗为51.113.(3)由于y=bx+a+e,可以算出i=yi-i,
分别为1=0.38,2=0.748,3=-0.47,4=-2.184,5=1.654.残差平方和:
eq
\o\al(2,i)≈8.43.(4)
(yi-)2=50.18,∴R2=1-≈0.832.所以解释变量小麦基本苗数对总效应约贡献了83.2%.残差变量贡献了约1-83.2%=16.8%.点评:要熟悉刻画回归效果的三种方式(1)残差图法:残差点比较均匀地落在水平的带状区域内说明选用的模型比较合适.(2)残差平方和法:残差平方和(yi-)2越小,模型的拟合效果越好.(3)R2法:R2=1-越接近1,表明回归的效果越好.巩
固 甲、乙、丙、丁4位同学各自对A,B两变量进行回归分析,分别得到散点图与残差平方和(yi-i)2如表所示:甲乙丙丁散点图残差平方和115106124103哪位同学的试验结果体现拟合A,B两变量关系的模型拟合精度高( )A.甲
B.乙
C.丙
D.丁解析:根据线性相关的知识,散点图中各样本点条状分布越均匀,同时保持残差平方和越小(对于已经获取的样本数据,R2的表达式中(yi-i)2为确定的数,则残差平方和越小,R2越大),由回归分析建立的线性回归模型的拟合效果越好,由试验结果知丁要好些.故选D.答案:D题型三
非线性回归分析例3 某地区不同身高的未成年男性的体重平均值如下表:身高x/cm60708090100110体重y/kg6.137.909.9912.1515.0217.50身高x/cm120130140150160170体重y/kg20.9226.8631.1138.8547.2555.05试建立y与x之间的回归方程.解析:根据上表中的数据画出散点图(如下图所示):由图看出,样本点分布在某条指数函数曲线的周围,于是令z=ln
y.x60708090100110z1.812.072.302.502.712.86x120130140150160170z3.043.293.443.663.864.01画出散点图(如下图所示):由表中数据可得z与x之间的回归直线方程:=0.693+0.020x,则有=e0.693+0.020x.点评:三种常见的非线性回归模型的处理方法:①指数函数型y=ebx+a,两边取对数得ln
y=ln
ebx+a,即ln
y=bx+a,令z=ln
y,把原始数据(x,y)转化为(x,z),再根据线性回归模型的方法求出a,b.②对数函数型y=bln
x+a,设x′=ln
x,原方程可化为y=bx′+a,再根据线性回归模型的方法求出a,b.③二次函数型y=bx2+a,设x′=x2,原方程可化为y=bx′+a,再根据线性回归模型的方法求出a,b.巩
固 若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,由例3中求出的回归方程,那么这个地区一名身高为175
cm,体重为82
kg的在校男生体重是否正常?解析:当x=175时,预测平均体重=e0.693+0.020×175≈66.22,由于66.22×1.2≈79.46<82,所以这个男生偏胖.题型四 线性回归分析的应用例4 以下是某地搜集到的新房屋的销售价格y(万元)和房屋的面积x(m2)的数据房屋面积x/m211511080135105销售价格y/万元24.821.618.429.222(1)画出数据对应的散点图;(2)求线性回归方程,
并在散点图中加上回归直线;(3)据(2)的结果估计当房屋面积为150
m2时的销售价格.解析:(1)数据对应的散点图如图所示:(2)=i=109,
lxy=(xi-)2=1
570,=23.2,lxx=(xi-)(
yi-)=308.设所求回归直线方程为=x+,则==≈0.196
2,=-
=1.816
6.故所求回归直线方程为=0.196
2x+1.816
6.(3)据(2),当x=150
m2时,销售价格的估计值为=0.196
2×150+1.816
6=31.246
6(万元).点评:已知x与y呈线性相关关系,就无需进行相关性检验,否则要进行相关性检验.如果两个变量不具备相关关系,或者相关关系不显著,即使求出回归方程也是毫无意义的,用其估计和预测也是不可信的.进行线性相关的判断,可通过散点图直观判断,散点图不明显的可进行相关性检验.巩
固 某农场对单位面积化肥用量x(kg)和水稻相应产量y(kg)的关系作了统计,得到数据如下:x15202530354045y330345365405445450455如果x与y之间具有线性相关关系,求出回归直线方程,并预测当单位面积化肥用量为32
kg时水稻的产量大约是多少(精确到0.01
kg).解析:(1)
列表如下:序号xyx2xy1153302254
9502203454006
9003253656259
12543040590012
1505354451
22515
5756404501
60018
0007454552
02520
475∑2102
7957
00087
175=×210=30,=×2
795≈399.3,=≈4.746,=399.3-4.746×30=256.92.y对x的回归直线方程为=256.92+4.746x.当x=32时,=256.92+4.746×32≈408.79.即回归直线方程为=256.92+4.746x.当单位面积化肥用量为32
kg时,水稻的产量约为408.79
kg.题型五 相关分析项例5 某同学6次考试的数学、语文成绩在班中的排名如下表:数学名次x765321语文名次y13119642对上述数据分别用=x+与=x2+来拟合y与x之间的关系,并用残差分析两者的拟合效果.解析:首先用=x+来拟合y与x之间的关系.因为=4,=7.5,(xi-)(yi-)=50,(xi-)2=28,所以==≈1.786,=-eq
\o(x,\s\up6(-))=0.356.所以=1.786x+0.356,此时的残差平方和为(yi-i)2≈0.214.再用=x2+来拟合y与x之间的关系.令t=x2,则对应表中数据为t493625941y13119642因为=20.667,=7.5,(ti-)(yi-)=400,(ti-)2≈1
857.333,所以==≈0.215,=-eq
\o(t,\s\up6(-))≈3.057.所以=0.215x+3.057,此时的残差平方和为(yi-i)2≈3.355.因为3.355>0.214,所以用=x+来拟合y与x之间的关系效果较好.点评:(1)残差平方和越小,预报精确度越高.(2)相关指数R2取得越大,说明模型的拟合效果越好.
巩
固 已知某校5个学生的数学和物理成绩如下:学生的编号12345数学成绩x8075706560物理成绩y7066686462(1)通过大量事实证明发现,一个学生的数学成绩和物理成绩是具有很强的线性相关关系的,在上述表格中,用x表示数学成绩,用y表示物理成绩,求y关于x的回归方程.(2)利用残差分析回归方程的拟合效果,若残差和在(-0.1,0.1)范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.解析:(1)由已知数据得,=70,=66,
代入公式,可求得=0.36,=40.8,故回归直线方程为=0.36x+40.8.(2)由=0.36x+40.8可知1=0.36×80+40.8=69.6,同理可得2=67.8,3=66,4=64.2,5=62.4,所以(yi-i)=0∈(-0.1,0.1),故该回归方程是“优拟方程”.(线性回归)A组1.下列变量具有相关关系的是( )A.人的身高与视力B.角的大小与所对的圆弧长C.直线上某点的横坐标与纵坐标D.人的年龄与身高答案:D2.在对两个变量x、y进行线性回归分析时一般有下列步骤:
①对所求出的回归方程作出解释;②收集数据(xi,yi),i=1,2,…,n;③求线性回归方程;④求相关系数;⑤根据所搜集的数据绘制散点图.如果根据可靠性要求能够判定变量x,y具有线性相关性,则在下列操作顺序中正确的是( )A.①②⑤③④
B.③②④⑤①C.②④③①⑤
D.②⑤④③①答案:D3.下列关于线性回归的判断,正确的个数是( )①若散点图中的所有点都在一条直线附近,则这条直线为回归直线;②散点图中的绝大多数点都线性相关,个别特殊点不影响线性回归,如图中的A,B,C点;③已知回归直线方程为=0.50x-0.81,则x=25时,y的估计值为11.69;④线性回归方程的意义是它反映了样本整体的变化趋势.A.0个
B.1个
C.2个
D.3个解析:因为由最小二乘法求得的回归方程直线才是真正的回归直线,所以①错;将x=25代入=0.50x-0.81得=11.69,所以③正确;根据回归方程的概念知②④也正确.故选D.答案:DB组一、选择题1.下列4个散点图中,不能用回归模型拟合的两个变量是( )解析:观察散点图可知,选项B中的点近似分布在一条抛物线附近,可以转化为线性回归模型;选项C、D中的点近似分布在一条直线附近,选项A中的点无规律.故选A.答案:A2.下表给出5组数据(x,y),为选出4组数据使线性相关程度最大,且保留第1组数据,则应去掉( )i12345xi-5-4-3-24yi-3-24-16A.第2组
B.第3组
C.
第4组
D.
第5组解析:作出散点图,可知,去掉第3组(-3,4)后的4组数据大致分布在一条直线附近.故选B.答案:B3.对于线性相关系数r,下列说法中正确的是( )A.|r|∈(-∞,+∞),|r|越大,相关程度越大;反之,相关程度越小B.|r|≤1,r越大,相关程度越大;反之,相关程度越小C.|r|≤1,且|r|越接近于1,相关程度越大;|r|越接近于0,相差程度越小D.以上说法都不正确答案:C4.工人月工资y(元)关于劳动生产率x(千元)的回归方程为=650+80x,下列说法中正确的个数是( )①劳动生产率为1
000元时,工资为730元;②劳动生产率提高1
000元时,则工资提高80元;③劳动生产率提高1
000元时,则工资提高730元;④当月工资为810元时,劳动生产率约为2
000元.A.1个
B.2个
C.3个
D.4个答案:C5.某产品的广告费用x(万元)与销售额y(万元)的统计数据如下表:广告费用x/万元4235销售额y/万元49263954根据上表可得回归方程=x+中的为9.4,据此模型预报广告费用为6万元时销售额为( )A.63.6万元
B.65.5万元
C.67.7万元
D.72.0万元解析:由表可计算==,==42,因为点在回归直线=x+上,且为9.4,所以42=9.4×+,
解得=9.1,故回归方程为=9.4x+9.1,
令x=6,得=65.5(万元),选B.答案:B二、填空题6.已知关于两个变量x、y
的回归方程为=1.5x+45,x∈{1,5,7,13,19},则=__________.解析:易知=9,因为=1.5+45,所以=1.5+45=1.5×9+45=58.5.答案:58.57.若对于变量y与x的10组统计数据的回归模型中,R2=0.95,又知残差平方和为120.53,那么(yi-)2的值为________________.解析:依题意有0.95=1-,所以(yi-)2=2
410.6.答案:2
410.68.某数学老师身高176
cm,他爷爷、父亲和儿子的身高分别是173
cm,170
cm和182
cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________cm.答案:185三、解答题9.在10年期间,一城市居民年收入与某种商品的销售额之间的关系见下表:第几年城市居民年收入x/亿元某商品的销售额y/万元132.225.0231.130.0332.934.0435.837.0537.139.0638.041.0739.042.0843.044.0944.648.01046.051.0(1)画出散点图;(2)如果散点图中各点大致分布在一条直线的附近,求y与x之间的线性回归方程;(3)试预测居民年收入50亿元时这种商品的销售额.解析:(1)散点图如下图所示:(2)观察散点图可知各点大致分布在一条直线的附近.列表,利用计算器进行计算:序号xiyixyxiyi132.225.01
036.84625805231.130.0967.21900933332.934.01
082.411
1561
118.6435.837.01
281.641
3691
324.6537.139.01
376.411
5211
446.9638.041.01
4441
6811
558739.042.01
5211
7641
638843.044.01
8491
9361
892944.648.01
989.162
3042
140.81046.051.02
1162
6012
346∑379.739114
663.6715
85715
202.9==≈1.447,=-=39.1-1.447×37.97≈-15.84,故所求线性回归方程为=1.447x-15.84.(3)根据上面求得的线性回归方程,当居民年收入50亿元时,=1.447×50-15.84=56.51(万元),即这种商品销售额大约为56.51万元.10.为了研究三月下旬的平均气温x(℃)与四月二十号前棉花害虫化蛹高峰日y的关系,某地区观察了2007年至2012年的情况,得到下面的数据:年份200720082009201020112012x/℃24.429.632.928.730.328.9y19611018据气象台预测,该地区在2013年三月下旬平均气温为27
℃,试估计2013年四月化蛹高峰日为哪天.解析:画出x与y的散点图可知,x与y有线性相关关系(图略).=i=29.13,=i=7.5,=5
130.92,iyi=1
222.6,∴==-2.2,=-=7.5-(-2.2)×29.13=71.6.∴回归直线方程为=-2.2x+71.6.当x=27时,=-2.2×27+71.6=12.2.据此,可估计该地区2013年4月12日或13日为化蛹高峰日.
A组1.有下列说法:①线性回归分析就是由样本点去寻找一条直线贴近这些样本点的数学方法;②利用样本点的散点图可以直观判断两个变量是否具有线性关系;③通过回归方程=x+及其回归系数,可以估计变量的取值和变化趋势;④因为由任何一组观测值都可以求得一个回归直线方程,所以没有必要进行相关性检验.其中正确命题的个数是( )A.1个
B.2个
C.3个
D.4个答案:C2.有下列说法:①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;②用相关指数R2来刻画回归的效果,R2值越大,说明模型的拟合效果越好;③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型,拟合效果越好.其中正确命题的个数是( )A.0个
B.1个
C.2个
D.3个答案:D3.某考察团对全国10个城市进行职工人均工资水平x(千元)与居民人均消费水平y(千元)统计调查,y与x具有相关关系,回归方程为=0.66x+1.562.若某城市居民人均消费水平为7.675(千元),估计该城市人均消费额占人均工资收入的百分比约为( )A.83%
B.72%
C.67%
D.66%解析:由已知=7.675,代入方程=0.66x+1.562,得x≈9.262
1,所以百分比为=83%.故选A.答案:AB组一、选择题1.
下面两个变量间的关系不是函数关系的是( )A.正方形的棱长与体积B.角的度数与它的余弦值C.
单产量为常数时,土地面积与粮食总产量D.日照时间与水稻亩产量解析:选项D为相关关系,其余均为函数关系.故选D.答案:D2.可用来分析身高与体重有关系的是( )A.残差分析
B.回归分析
C.等高条形图
D.独立检验解析:因为身高与体重是两个具有相关关系的变量,所以要用回归分析来解决.故选B.答案:B3.已知x,y取值如下表:x014568y1.31.85.66.17.49.3从所得的散点图分析可知:y与x线性相关,且=0.95x+a,则a=( )A.1.30
B.1.45
C.1.65
D.1.80解析:易得=4,=5.25,因线性回归方程通过样本点中心(,),故有5.25=0.95×4+a,所以a=1.45.故选B.答案:B4.四名同学根据各自的样本数据研究变量x、y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:①y与x负相关且=2.347x-6.423;②y与x负相关且=-3.476x+5.648;③y与x正相关且=5.437x+8.493;④y与x正相关且=-4.326x-4.578.其中一定不正确的结论的序号是( )A.①②
B.②③
C.③④
D.①④解析:x的系数大于0为正相关,小于0为负相关.
故选D.答案:D5.已知两个变量x和y之间具有线性相关性,甲、乙两个同学各自独立地做了10次和15次试验,并且利用线性回归的方法求得回归直线分别为l1和l2.已知两个人在试验中发现对变量x的观测数据的平均数都为s,对变量y的观测数据的平均数都是t,则下列说法中正确的是( )A.l1与l2可能有交点(s,t)B.l1与l2相交,但交点一定不是(s,t)C.l1与l2必定平行D.l1与l2必定重合答案:A二、填空题6.若一组观测值(x1,
y1),(x2,y2),…,(xn,yn)之间满足yi=bxi+a+ei
(i=1,2,…,n),ei恒为0,则R2为________.答案:17.已知两个变量x和y线性相关,5次试验的观测数据如下:x100120140160180y4554627592那么变量y关于x的回归方程是____________.答案:=0.575x-14.98.若某地财政收入x与支出y满足线性回归方程=x++ε(单位:亿元),其中=0.8,=2,|ε|≤0.5,如果今年该地区财政收入10亿元,则年支出预计不会超过________________亿元.解析:将x=10代入线性回归方程,得=0.8×10+2+ε=10+ε,因为|ε|≤0.5,所以=10+ε≤10.5.答案:10.5三、解答题9.在试验中得到变量y与x的数据(见下表):x0.066
70.038
80.033
30.027
30.022
5y39.442.941.043.149.2由经验知,y与之间具有线性相关关系,试求y与x之间的回归曲线方程;
当x0=0.038时,预测y0的值.分析:通过换元转化为线性回归问题.解析:令u=,由题目所给数据可得下表所示的数据:序号uiyiuuiyi115.039.4225591225.842.9665.641
106.82330.041.09001
230436.643.11
339.561
577.46544.449.21
971.362
184.48合计151.8215.65
101.566
689.76计算得=0.29,=34.32.∴=34.32+0.29u.所求回归曲线方程为=34.32+.当x0=0.038时,y0=34.32+≈41.95.10.在一段时间内,某种商品的价格x(元)和需求量y(件)之间的一组数据为:价格x/元1416182022需求量y/件1210753求出y对x的回归直线方程,并说明拟合效果的好坏.解析:=×(14+16+18+20+22)=18,=(12+10+7+5+3)=7.4,=142+162+182+202+222=1
660,=122+102+72+52+32=327,iyi=14×12+16×10+18×7+20×5+22×3=620,所以=
==-=-1.15,所以=7.4+1.15×18=28.1,所以回归直线方程为=-1.15x+28.1,列出残差表为:yi-i00.3-0.4-0.10.2yi-4.62.6-0.4-2.4-4.4所以(yi-i)2=0.3,(yi-)2=53.2,R2=1-≈0.994,因而拟合效果较好.
PAGE
