2012年浙江省普通高中会考数学(含答案)
文档属性
| 名称 | 2012年浙江省普通高中会考数学(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 82.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-25 10:01:29 | ||
图片预览

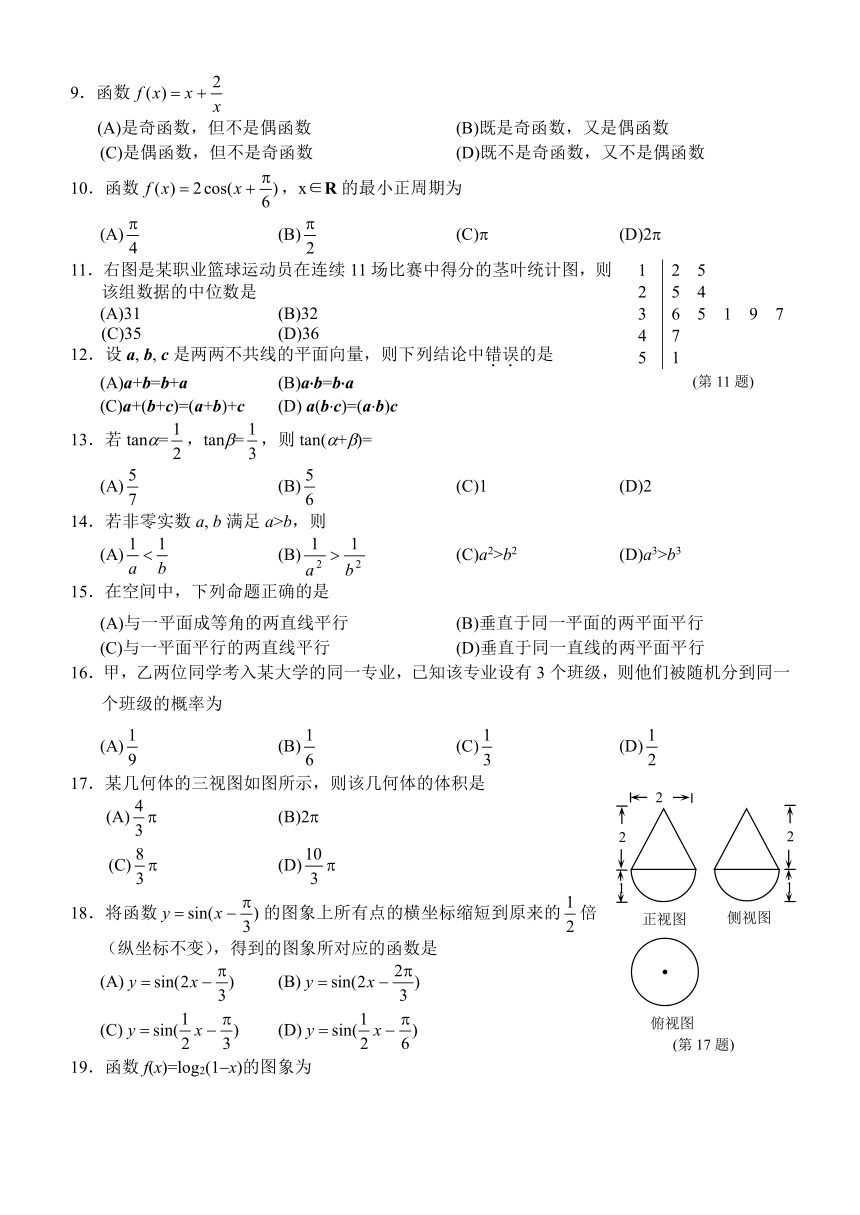


文档简介
2012年浙江省普通高中会考
数 学
考生须知:
1.全卷分试卷Ⅰ、Ⅱ和答卷Ⅰ、Ⅱ.试卷共6页,有四大题,42小题,其中第二大题为选做题,其余为必做题,满分为100分.考试时间120分钟.
2.本卷答案必须做在答卷Ⅰ、Ⅱ的相应位置上,做在试卷上无效.
3.请用铅笔将答卷Ⅰ上的准考证号和学科名称所对应的括号或方框内涂黑,请用钢笔或圆珠笔将姓名、准考证号分别填写在答卷Ⅰ、Ⅱ的相应位置上.
4.参考公式:
球的表面积公式:S=4 R2 球的体积公式:(其中R为球的半径)
试 卷 Ⅰ
一、选择题(本题有26小题,1 20每小题2分,21 26每小题3分,共58分.选出各题中一个符合题意的正确选项,不选、多选、错选均不给分)
1.设全集U={1,2,3,4},则集合A={1, 3},则CUA=
(A){1, 4} (B){2, 4} (C){3, 4} (D){2, 3}
2.sin=
(A) (B) (C) (D)1
3.函数的定义域为
(A) {x|x<1} (B){x|x>1|} (C){x∈R|x≠0} (D){x∈R|x≠1}
4.若直线y=kx+2的斜率为2,则k=
(A) 2 (B) (C) (D)
5.若函数f(x)为
x 0 1 2 3
f(x) 3 2 1 0
则f[f(1)]=
(A)0 (B)1 (C) (D)3
6.以矩形的一边所在的直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体是
(A)球 (B)圆台 (C)圆锥 (D)圆柱
7.圆x2+y2 4x+6y+3=0的圆心坐标是
(A)(2, 3) (B)( 2, 3) (C)(2, 3) (D)( 2, 3)
8.等比数列{an}中,a3=16,a4=8,则a1=( )
(A)64 (B)32 (C)4 (D)2
9.函数
(A)是奇函数,但不是偶函数 (B)既是奇函数,又是偶函数
(C)是偶函数,但不是奇函数 (D)既不是奇函数,又不是偶函数
10.函数,x∈R的最小正周期为
(A) (B) (C) (D)2
1
2
3
45 2 5
5 4
6 5 1 9 7
71
11.右图是某职业篮球运动员在连续11场比赛中得分的茎叶统计图,则该组数据的中位数是
(A)31 (B)32
(C)35 (D)36
12.设a, b, c是两两不共线的平面向量,则下列结论中错误的是
(A)a+b=b+a (B)ab=ba
(C)a+(b+c)=(a+b)+c (D) a(bc)=(ab)c
13.若tan =,tan =,则tan( + )=
(A) (B) (C)1 (D)2
14.若非零实数a, b满足a>b,则
(A) (B) (C)a2>b2 (D)a3>b3
15.在空间中,下列命题正确的是
(A)与一平面成等角的两直线平行 (B)垂直于同一平面的两平面平行
(C)与一平面平行的两直线平行 (D)垂直于同一直线的两平面平行
16.甲,乙两位同学考入某大学的同一专业,已知该专业设有3个班级,则他们被随机分到同一个班级的概率为
(A) (B) (C) (D)
17.某几何体的三视图如图所示,则该几何体的体积是
(A) (B)2
(C) (D)
18.将函数的图象上所有点的横坐标缩短到原来的倍(纵坐标不变),得到的图象所对应的函数是
(A) (B)
(C) (D)
19.函数f(x)=log2(1 x)的图象为
20.如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是
(A)30 (B)45
(C)60 (D)90
21.若{an}无穷等比数列,则下列数列可能不是等比数列的是
(A){a2n} (B){a2n 1}
(C){anan+1} (D){an+an+1}
22.若log2x+log2y=3,则2x+y的最小值是
(A) (B)8 (C)10 (D)12
23.右图是某同学用于计算S=sin1+sin2+sin3+…+sin2012值的程序框图,则在判断框中填写
(A)k>2011 (B)k>2012
(C)k<2011 (D)k<2012
24.M是空间直角坐标系Oxyz中任一点(异于O),若直线OM与xOy平面,yoz平面,zox平面所成的角的余弦值分别为p, q, r,则p2+q2+r2=
(A) (B)1
(C) 2 (D)
25.设圆C:(x 5)2+(y 3)2=5,过圆心C作直线l与圆交于A,B两点,与x轴交于P点,若A恰为线段BP的中点,则直线l的方程为
(A)x 2y+1=0,x+2y 11=0 (B)2x y 7=0,2x+y 13=0
(C)x 3y+4=0,x+3y 14=0 (D)3x y 12=0,3x+y 18=0
26.在平面直角坐标系xOy中,设不等式组,所表示的平面区域为D,若D的边界是菱形,则ab=
(A) (B) (C) (D)
二、选择题(本题分A、B两组,任选一组完成,每组各4小题,选做B组的考生,填涂时注意第27-30题留空;若两组都做,以27-30题记分. 每小题3分,共12分,选出各题中一个符合题意的正确选项,不选、多选、错选均不给分)
A组
27.i是虚数单位,=
(A)1+i (B)1 i (C)2+2i (D)2 2i
28.对于集合A,B,“A∩B=A∪B”是“A=B”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件 (D)既不充分又不必要条件
29.在椭圆中,F,A,B分别为其左焦点,右顶点,上顶点,O为坐标原点,M为线段OB的中点,若 FMA为直角三角形,则该椭圆的离心率为
(A) (B) (C) (D)
30.设函数y=f(x),x∈R的导函数为,且f( x)=f(x),,则下列不等式成立的是
(A)f(0)(C) e2f(2)注:e为自然对数的底数
B组
31.双曲线的渐近线方程为
(A)3x±4y=0 (B) 4x±3y=0 (C) 3x±5y=0 (D)5x±3y=0
32.若随机变量X~B(100, p),X的数学期望EX=24,则p的值是
(A) (B) (C) (D)
33.将a, b, c, d, e五个字母填入右图的五个方格中,每个方格恰好填一个字母,则a, b不填在相邻两个格子(即它们有一条公共边)中的填法数为
(A)72 (B)96
(C)116 (D)120
34.在棱长为1的正方体ABCD-A1B1C1D1中,M是BC的中点,P, Q是正方体内部及面上的两个动点,则的最大值是
(A) (B) 1 (C) (D)
试 卷 Ⅱ
请将本卷的答案用钢笔或圆珠笔写在答卷Ⅱ上.
三、填空题(本题有5小题,每小题2分,共10分)
35.不等式x2 2x<0的解集是 .
36.设Sn是等差数列{an}的前n项和,若a1= 2,S4=10,则公差d= .
37.某校对学生在一周中参加社会实践活动时间进行调查,现从中抽取一个容量为n的样本加以分析,其频率分布直方图如图所示,已知时间不超过2小时的人数为12人,则n= .
38.设点A(x1,f(x1)),B(x2,f(x2)),T(x0,f(x0))在函数f(x)=x3 ax(a>0)的图象上,其中x1,x2是f(x)的两个极值点,x0(x0≠0)是f(x)的一个零点,若函数f(x)的图象在T处的切线与直线AB垂直,则a= .
39.在数列{an}中,设S0=0,Sn=a1+a2+a3+…+an,其中1≤k≤n,k,n∈N*,当n≤14时,使Sn=0的n的最大值为 .
四、解答题(本题有3小题,共20分)
40.(本题6分)
在锐角 ABC中,角A, B, C所对的边分别为a, b, c. 已知b=2,c=3,sinA=. 求 ABC的面积及a的值.
41.(本题6分)
设抛物线C:y=x2,F为焦点,l为准线,准线与y轴的交点为H.
(I)求|FH|;
(II)设M是抛物线C上一点,E(0, 4),延长ME,MF分别交C于点A,B.若A, B, H三点共线,求点M的坐标.
42.(本题8分)
设函数f(x)=(x a)ex+(a 1)x+a,a∈R.
(I)当a=1时,求f(x)的单调区间;
(II)(i)设g(x)是f(x)的导函数,证明:当a>2时,在(0,+∞)上恰有一个x0使得g(x0)=0;
(ii)求实数a的取值范围,使得对任意的x∈[0, 2],恒有f(x)≤0成立.
注:e为自然对数的底数.
浙江省2012届数学会考答案
一、二、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D B B D C A A D
题号 11 12 13 14 15 16 17 18 19 20
答案 C D C D D D A A A D
题号 21 22 23 24 25 26 27 28 29 30
答案 D B B C A B B C A D
三、填空题
35、 ; 36、3 ; 37、150 ; 38、 ; 39、12
四、解答题
40、解:
41、解:(Ⅰ)由抛物线方程知抛物线的焦点坐标为,准线方程为。
因此点H坐标为,所以
(Ⅱ)设
则。
因为H、A、B三点共线,所以
即(*)
由,所以
同理可得,所以①
所以②
把①②式代入式子(*)并化简得,所以
所以点M坐标为(-2,4)或(2,4)
另解:因为H、A、B三点共线,
又,,,所以
所以点M坐标为(-2,4)或(2,4)
42、解:(Ⅰ)当时,
当时,;当时,
所以函数的减区间是;增区间是
(Ⅱ)(ⅰ)
当时,;当时,
因为,所以函数在上递减;在上递增
又因为,
所以在上恰有一个使得
(ⅱ)由题意知,即
由(ⅰ)知(0,)递减,(,+∞)递增,
设在上最大值为,
任意的x∈[0, 2],恒有f(x)≤0,即,得
(第11题)
正视图
俯视图
侧视图
(第17题)
2
2
1
2
1
1
x
y
O
(A)
1
x
y
O
(B)
1
x
y
O
(C)
1
x
y
O
(D)
A
B
C
S
(第20题)
开始
结束
输出S
k=1
S=S+sink
k=k+1
是
否
(第23题)
S=0
O
2
4
6
8
10
0.04
频率/组距
时间/小时
(第13题)
0.08
0.10
0.12
0.16
x
y
O
E
B
A
M
F
(第41题)
数 学
考生须知:
1.全卷分试卷Ⅰ、Ⅱ和答卷Ⅰ、Ⅱ.试卷共6页,有四大题,42小题,其中第二大题为选做题,其余为必做题,满分为100分.考试时间120分钟.
2.本卷答案必须做在答卷Ⅰ、Ⅱ的相应位置上,做在试卷上无效.
3.请用铅笔将答卷Ⅰ上的准考证号和学科名称所对应的括号或方框内涂黑,请用钢笔或圆珠笔将姓名、准考证号分别填写在答卷Ⅰ、Ⅱ的相应位置上.
4.参考公式:
球的表面积公式:S=4 R2 球的体积公式:(其中R为球的半径)
试 卷 Ⅰ
一、选择题(本题有26小题,1 20每小题2分,21 26每小题3分,共58分.选出各题中一个符合题意的正确选项,不选、多选、错选均不给分)
1.设全集U={1,2,3,4},则集合A={1, 3},则CUA=
(A){1, 4} (B){2, 4} (C){3, 4} (D){2, 3}
2.sin=
(A) (B) (C) (D)1
3.函数的定义域为
(A) {x|x<1} (B){x|x>1|} (C){x∈R|x≠0} (D){x∈R|x≠1}
4.若直线y=kx+2的斜率为2,则k=
(A) 2 (B) (C) (D)
5.若函数f(x)为
x 0 1 2 3
f(x) 3 2 1 0
则f[f(1)]=
(A)0 (B)1 (C) (D)3
6.以矩形的一边所在的直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体是
(A)球 (B)圆台 (C)圆锥 (D)圆柱
7.圆x2+y2 4x+6y+3=0的圆心坐标是
(A)(2, 3) (B)( 2, 3) (C)(2, 3) (D)( 2, 3)
8.等比数列{an}中,a3=16,a4=8,则a1=( )
(A)64 (B)32 (C)4 (D)2
9.函数
(A)是奇函数,但不是偶函数 (B)既是奇函数,又是偶函数
(C)是偶函数,但不是奇函数 (D)既不是奇函数,又不是偶函数
10.函数,x∈R的最小正周期为
(A) (B) (C) (D)2
1
2
3
45 2 5
5 4
6 5 1 9 7
71
11.右图是某职业篮球运动员在连续11场比赛中得分的茎叶统计图,则该组数据的中位数是
(A)31 (B)32
(C)35 (D)36
12.设a, b, c是两两不共线的平面向量,则下列结论中错误的是
(A)a+b=b+a (B)ab=ba
(C)a+(b+c)=(a+b)+c (D) a(bc)=(ab)c
13.若tan =,tan =,则tan( + )=
(A) (B) (C)1 (D)2
14.若非零实数a, b满足a>b,则
(A) (B) (C)a2>b2 (D)a3>b3
15.在空间中,下列命题正确的是
(A)与一平面成等角的两直线平行 (B)垂直于同一平面的两平面平行
(C)与一平面平行的两直线平行 (D)垂直于同一直线的两平面平行
16.甲,乙两位同学考入某大学的同一专业,已知该专业设有3个班级,则他们被随机分到同一个班级的概率为
(A) (B) (C) (D)
17.某几何体的三视图如图所示,则该几何体的体积是
(A) (B)2
(C) (D)
18.将函数的图象上所有点的横坐标缩短到原来的倍(纵坐标不变),得到的图象所对应的函数是
(A) (B)
(C) (D)
19.函数f(x)=log2(1 x)的图象为
20.如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是
(A)30 (B)45
(C)60 (D)90
21.若{an}无穷等比数列,则下列数列可能不是等比数列的是
(A){a2n} (B){a2n 1}
(C){anan+1} (D){an+an+1}
22.若log2x+log2y=3,则2x+y的最小值是
(A) (B)8 (C)10 (D)12
23.右图是某同学用于计算S=sin1+sin2+sin3+…+sin2012值的程序框图,则在判断框中填写
(A)k>2011 (B)k>2012
(C)k<2011 (D)k<2012
24.M是空间直角坐标系Oxyz中任一点(异于O),若直线OM与xOy平面,yoz平面,zox平面所成的角的余弦值分别为p, q, r,则p2+q2+r2=
(A) (B)1
(C) 2 (D)
25.设圆C:(x 5)2+(y 3)2=5,过圆心C作直线l与圆交于A,B两点,与x轴交于P点,若A恰为线段BP的中点,则直线l的方程为
(A)x 2y+1=0,x+2y 11=0 (B)2x y 7=0,2x+y 13=0
(C)x 3y+4=0,x+3y 14=0 (D)3x y 12=0,3x+y 18=0
26.在平面直角坐标系xOy中,设不等式组,所表示的平面区域为D,若D的边界是菱形,则ab=
(A) (B) (C) (D)
二、选择题(本题分A、B两组,任选一组完成,每组各4小题,选做B组的考生,填涂时注意第27-30题留空;若两组都做,以27-30题记分. 每小题3分,共12分,选出各题中一个符合题意的正确选项,不选、多选、错选均不给分)
A组
27.i是虚数单位,=
(A)1+i (B)1 i (C)2+2i (D)2 2i
28.对于集合A,B,“A∩B=A∪B”是“A=B”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件 (D)既不充分又不必要条件
29.在椭圆中,F,A,B分别为其左焦点,右顶点,上顶点,O为坐标原点,M为线段OB的中点,若 FMA为直角三角形,则该椭圆的离心率为
(A) (B) (C) (D)
30.设函数y=f(x),x∈R的导函数为,且f( x)=f(x),,则下列不等式成立的是
(A)f(0)
B组
31.双曲线的渐近线方程为
(A)3x±4y=0 (B) 4x±3y=0 (C) 3x±5y=0 (D)5x±3y=0
32.若随机变量X~B(100, p),X的数学期望EX=24,则p的值是
(A) (B) (C) (D)
33.将a, b, c, d, e五个字母填入右图的五个方格中,每个方格恰好填一个字母,则a, b不填在相邻两个格子(即它们有一条公共边)中的填法数为
(A)72 (B)96
(C)116 (D)120
34.在棱长为1的正方体ABCD-A1B1C1D1中,M是BC的中点,P, Q是正方体内部及面上的两个动点,则的最大值是
(A) (B) 1 (C) (D)
试 卷 Ⅱ
请将本卷的答案用钢笔或圆珠笔写在答卷Ⅱ上.
三、填空题(本题有5小题,每小题2分,共10分)
35.不等式x2 2x<0的解集是 .
36.设Sn是等差数列{an}的前n项和,若a1= 2,S4=10,则公差d= .
37.某校对学生在一周中参加社会实践活动时间进行调查,现从中抽取一个容量为n的样本加以分析,其频率分布直方图如图所示,已知时间不超过2小时的人数为12人,则n= .
38.设点A(x1,f(x1)),B(x2,f(x2)),T(x0,f(x0))在函数f(x)=x3 ax(a>0)的图象上,其中x1,x2是f(x)的两个极值点,x0(x0≠0)是f(x)的一个零点,若函数f(x)的图象在T处的切线与直线AB垂直,则a= .
39.在数列{an}中,设S0=0,Sn=a1+a2+a3+…+an,其中1≤k≤n,k,n∈N*,当n≤14时,使Sn=0的n的最大值为 .
四、解答题(本题有3小题,共20分)
40.(本题6分)
在锐角 ABC中,角A, B, C所对的边分别为a, b, c. 已知b=2,c=3,sinA=. 求 ABC的面积及a的值.
41.(本题6分)
设抛物线C:y=x2,F为焦点,l为准线,准线与y轴的交点为H.
(I)求|FH|;
(II)设M是抛物线C上一点,E(0, 4),延长ME,MF分别交C于点A,B.若A, B, H三点共线,求点M的坐标.
42.(本题8分)
设函数f(x)=(x a)ex+(a 1)x+a,a∈R.
(I)当a=1时,求f(x)的单调区间;
(II)(i)设g(x)是f(x)的导函数,证明:当a>2时,在(0,+∞)上恰有一个x0使得g(x0)=0;
(ii)求实数a的取值范围,使得对任意的x∈[0, 2],恒有f(x)≤0成立.
注:e为自然对数的底数.
浙江省2012届数学会考答案
一、二、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D B B D C A A D
题号 11 12 13 14 15 16 17 18 19 20
答案 C D C D D D A A A D
题号 21 22 23 24 25 26 27 28 29 30
答案 D B B C A B B C A D
三、填空题
35、 ; 36、3 ; 37、150 ; 38、 ; 39、12
四、解答题
40、解:
41、解:(Ⅰ)由抛物线方程知抛物线的焦点坐标为,准线方程为。
因此点H坐标为,所以
(Ⅱ)设
则。
因为H、A、B三点共线,所以
即(*)
由,所以
同理可得,所以①
所以②
把①②式代入式子(*)并化简得,所以
所以点M坐标为(-2,4)或(2,4)
另解:因为H、A、B三点共线,
又,,,所以
所以点M坐标为(-2,4)或(2,4)
42、解:(Ⅰ)当时,
当时,;当时,
所以函数的减区间是;增区间是
(Ⅱ)(ⅰ)
当时,;当时,
因为,所以函数在上递减;在上递增
又因为,
所以在上恰有一个使得
(ⅱ)由题意知,即
由(ⅰ)知(0,)递减,(,+∞)递增,
设在上最大值为,
任意的x∈[0, 2],恒有f(x)≤0,即,得
(第11题)
正视图
俯视图
侧视图
(第17题)
2
2
1
2
1
1
x
y
O
(A)
1
x
y
O
(B)
1
x
y
O
(C)
1
x
y
O
(D)
A
B
C
S
(第20题)
开始
结束
输出S
k=1
S=S+sink
k=k+1
是
否
(第23题)
S=0
O
2
4
6
8
10
0.04
频率/组距
时间/小时
(第13题)
0.08
0.10
0.12
0.16
x
y
O
E
B
A
M
F
(第41题)
同课章节目录
