2020-2021学年人教版九下数学课时训练28.2解直角三角形及其应用(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版九下数学课时训练28.2解直角三角形及其应用(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 568.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-21 13:00:26 | ||
图片预览




文档简介
28.2解直角三角形及其应用
一、选择题
王英同学从
地沿北偏西
方向走
到
地,再从
地向正东方向走
到
地,此时王英同学离
地
A.
B.
C.
D.
轮船航行到
处时,观测到小岛
的方向是北偏西
,那么同时从
处观测到轮船的方向是
A.南偏西
B.东偏西
C.南偏东
D.西偏东
如图,某时刻海上点
处有一客轮,测得灯塔
位于客轮
的北偏东
方向,且相距
海里.客轮以
海里/小时的速度沿北偏西
方向航行
小时到达
处,那么
为
A.
B.
C.
D.
如图,在矩形
中,
于点
,,,设
,则
的值为
A.
B.
C.
D.
如图是某水库大坝横断面示意图.其中
,
分别表示水库上下底面的水平线,,
的长是
,则水库大坝的高度
是
A.
B.
C.
D.
如图,一艘海轮位于灯塔
的南偏东
方向的
处,它以每小时
海里的速度向正北方向航行,
小时后到达位于灯塔
的北偏东
的
处,则
处与灯塔
的距离为
A.
海里
B.
海里
C.
海里
D.
海里
二、填空题
如图,某渔船在海面上朝正东方向匀速航行,在
处观测到灯塔
在北偏东
方向上,航行半小时后到达
处,此时观测到灯塔
在北偏东
方向上,那么该船继续航行
分钟可使渔船到达离灯塔距离最近的位置.
如图,某河道要建造一座公路桥,要求桥面离地面高度
为
米,引桥的坡角
为
,则引桥的水平距离
的长是
米(结果精确到
米).
如图,在高
米、坡角为
的楼梯表面铺地毯,地毯的长度至少需
米(结果精确到
米).
如图,在建筑平台
的顶部
处,测得大树
的顶部
的仰角为
,测得大树
的底部
的俯角为
,已知平台
的高度为
,则大树的高度为
(结果保留根号).
如图,四边形
中,,,若四边形
的面积为
,则
长是
.
一艘轮船在小岛
的北偏东
方向距小岛
海里的
处,沿正西方向航行
小时后到达小岛的北偏西
的
处,则该船行驶的速度为
海里
小时.
三、解答题
数学活动课上,老师和学生一起测量学校升旗台上旗杆
的高度.如图,老师测得升旗台前斜坡
的坡比为
(即
),学生小明站在离升旗台水平距离为
(即
)处的
点,测得旗杆顶端
的仰角为
,已知
,升旗台高
,小明身高
,请帮小明计算出旗杆
的高度.
如图,轮船从点
处出发,先航行至位于点
的南偏西
且与点
相距
的点
处,再航行至位于点
的北偏东
且与点
相距
的点
处.
(1)
求点
与点
的距离(精确到
);
(2)
确定点
相对于点
的方向.(参考数据:,
)
如图,某河堤的横断面是梯形
,,
于点
,
米,
米,,.求
的长度.
如图,斜坡
的坡度(坡比)为
,
米.坡顶有一旗杆
,旗杆顶端点
与点
有一条彩带
相连,
米.试求旗杆
的高度.
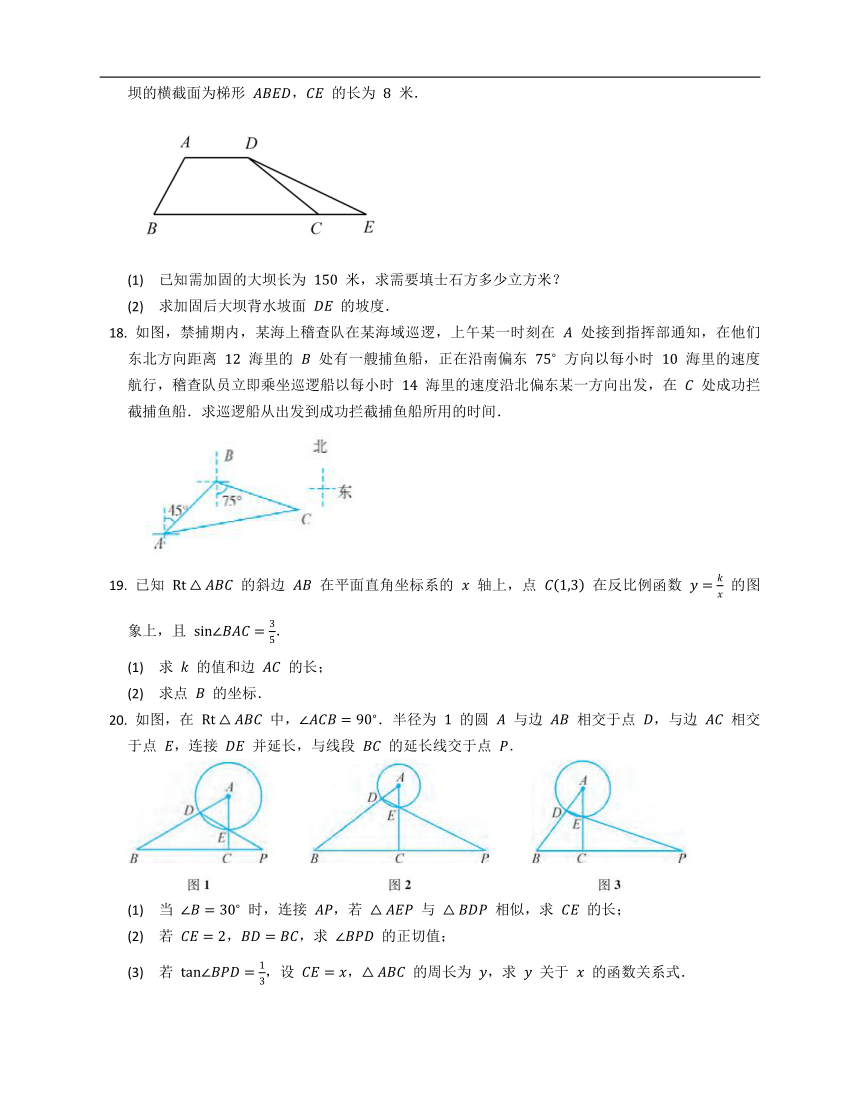
如图,水务部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形
,如图所示,已知迎水坡面
的长为
米,,背水坡面
长为
米,加固后大坝的横截面为梯形
,
的长为
米.
(1)
已知需加固的大坝长为
米,求需要填士石方多少立方米?
(2)
求加固后大坝背水坡面
的坡度.
如图,禁捕期内,某海上稽查队在某海域巡逻,上午某一时刻在
处接到指挥部通知,在他们东北方向距离
海里的
处有一艘捕鱼船,正在沿南偏东
方向以每小时
海里的速度航行,稽查队员立即乘坐巡逻船以每小时
海里的速度沿北偏东某一方向出发,在
处成功拦截捕鱼船.求巡逻船从出发到成功拦截捕鱼船所用的时间.
已知
的斜边
在平面直角坐标系的
轴上,点
在反比例函数
的图象上,且
.
(1)
求
的值和边
的长;
(2)
求点
的坐标.
如图,在
中,.半径为
的圆
与边
相交于点
,与边
相交于点
,连接
并延长,与线段
的延长线交于点
.
(1)
当
时,连接
,若
与
相似,求
的长;
(2)
若
,,求
的正切值;
(3)
若
,设
,
的周长为
,求
关于
的函数关系式.
答案
一、选择题
1.
【答案】D
2.
【答案】C
3.
【答案】A
4.
【答案】C
5.
【答案】A
6.
【答案】D
【解析】
(海里),
,,
,
,
海里.
二、填空题
7.
【答案】
8.
【答案】
9.
【答案】
10.
【答案】
【解析】如图,过点
作
于点
,
在
中,
,
,
在
中,
,
.
11.
【答案】
12.
【答案】
【解析】如图所示:
设该船行驶的速度为
海里
时,
小时后到达小岛的北偏西
的
处,
由题意得
海里,
海里,
在直角三角形
中,,
所以
,
所以
,,
在直角三角形
中,,
所以
,
所以
,
解得
.
即该船行驶的速度为
海里
时.
三、解答题
13.
【答案】
.
14.
【答案】
(1)
如图,过点
作
于点
,作
.
,
由图得,,
在
中,
,,
,,
,
在
中,由勾股定理得:.
点
与点
的距离约为
.
(2)
在
中,
,,
,
,
.
点
位于点
的南偏东
方向.
15.
【答案】过点
作
于点
.
,,,
,.
,,
.
.
,
(米).
16.
【答案】
米
17.
【答案】
(1)
立方米;
(2)
.
18.
【答案】
小时.
19.
【答案】
(1)
的值为
.
作
轴,垂足为点
,
因为
,
所以
,
又因为
,
所以
.
(2)
斜边
在直角坐标系的
轴上有两种情况:
①点
在点
的右边(如图
).
因为
,,
所以
.
在
中,,,则
,
因为
,
所以
,即
.
从而
(或
),
所以点
的坐标为
(或写成
).
②点
在点
的左边(如图
),
同理可得点
的坐标为
(或写成
).
20.
【答案】
(1)
如图
.
,,
.
,
为等边三角形,则
,
,,
从而
,故
为等腰三角形.
与
相似,
为等腰三角形,,故
.
(2)
如图
.
设
,,
,解得
,则
.
过
作
交
于
,
,则
,即
,
从而
,同理可得
.
,则
,,从而解得
.
,
.
(3)
如图
.
当
时,设
,
.
由()知
,.
设
,则
,
,,.
,解得
(舍),.
.
一、选择题
王英同学从
地沿北偏西
方向走
到
地,再从
地向正东方向走
到
地,此时王英同学离
地
A.
B.
C.
D.
轮船航行到
处时,观测到小岛
的方向是北偏西
,那么同时从
处观测到轮船的方向是
A.南偏西
B.东偏西
C.南偏东
D.西偏东
如图,某时刻海上点
处有一客轮,测得灯塔
位于客轮
的北偏东
方向,且相距
海里.客轮以
海里/小时的速度沿北偏西
方向航行
小时到达
处,那么
为
A.
B.
C.
D.
如图,在矩形
中,
于点
,,,设
,则
的值为
A.
B.
C.
D.
如图是某水库大坝横断面示意图.其中
,
分别表示水库上下底面的水平线,,
的长是
,则水库大坝的高度
是
A.
B.
C.
D.
如图,一艘海轮位于灯塔
的南偏东
方向的
处,它以每小时
海里的速度向正北方向航行,
小时后到达位于灯塔
的北偏东
的
处,则
处与灯塔
的距离为
A.
海里
B.
海里
C.
海里
D.
海里
二、填空题
如图,某渔船在海面上朝正东方向匀速航行,在
处观测到灯塔
在北偏东
方向上,航行半小时后到达
处,此时观测到灯塔
在北偏东
方向上,那么该船继续航行
分钟可使渔船到达离灯塔距离最近的位置.
如图,某河道要建造一座公路桥,要求桥面离地面高度
为
米,引桥的坡角
为
,则引桥的水平距离
的长是
米(结果精确到
米).
如图,在高
米、坡角为
的楼梯表面铺地毯,地毯的长度至少需
米(结果精确到
米).
如图,在建筑平台
的顶部
处,测得大树
的顶部
的仰角为
,测得大树
的底部
的俯角为
,已知平台
的高度为
,则大树的高度为
(结果保留根号).
如图,四边形
中,,,若四边形
的面积为
,则
长是
.
一艘轮船在小岛
的北偏东
方向距小岛
海里的
处,沿正西方向航行
小时后到达小岛的北偏西
的
处,则该船行驶的速度为
海里
小时.
三、解答题
数学活动课上,老师和学生一起测量学校升旗台上旗杆
的高度.如图,老师测得升旗台前斜坡
的坡比为
(即
),学生小明站在离升旗台水平距离为
(即
)处的
点,测得旗杆顶端
的仰角为
,已知
,升旗台高
,小明身高
,请帮小明计算出旗杆
的高度.
如图,轮船从点
处出发,先航行至位于点
的南偏西
且与点
相距
的点
处,再航行至位于点
的北偏东
且与点
相距
的点
处.
(1)
求点
与点
的距离(精确到
);
(2)
确定点
相对于点
的方向.(参考数据:,
)
如图,某河堤的横断面是梯形
,,
于点
,
米,
米,,.求
的长度.
如图,斜坡
的坡度(坡比)为
,
米.坡顶有一旗杆
,旗杆顶端点
与点
有一条彩带
相连,
米.试求旗杆
的高度.
如图,水务部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形
,如图所示,已知迎水坡面
的长为
米,,背水坡面
长为
米,加固后大坝的横截面为梯形
,
的长为
米.
(1)
已知需加固的大坝长为
米,求需要填士石方多少立方米?
(2)
求加固后大坝背水坡面
的坡度.
如图,禁捕期内,某海上稽查队在某海域巡逻,上午某一时刻在
处接到指挥部通知,在他们东北方向距离
海里的
处有一艘捕鱼船,正在沿南偏东
方向以每小时
海里的速度航行,稽查队员立即乘坐巡逻船以每小时
海里的速度沿北偏东某一方向出发,在
处成功拦截捕鱼船.求巡逻船从出发到成功拦截捕鱼船所用的时间.
已知
的斜边
在平面直角坐标系的
轴上,点
在反比例函数
的图象上,且
.
(1)
求
的值和边
的长;
(2)
求点
的坐标.
如图,在
中,.半径为
的圆
与边
相交于点
,与边
相交于点
,连接
并延长,与线段
的延长线交于点
.
(1)
当
时,连接
,若
与
相似,求
的长;
(2)
若
,,求
的正切值;
(3)
若
,设
,
的周长为
,求
关于
的函数关系式.
答案
一、选择题
1.
【答案】D
2.
【答案】C
3.
【答案】A
4.
【答案】C
5.
【答案】A
6.
【答案】D
【解析】
(海里),
,,
,
,
海里.
二、填空题
7.
【答案】
8.
【答案】
9.
【答案】
10.
【答案】
【解析】如图,过点
作
于点
,
在
中,
,
,
在
中,
,
.
11.
【答案】
12.
【答案】
【解析】如图所示:
设该船行驶的速度为
海里
时,
小时后到达小岛的北偏西
的
处,
由题意得
海里,
海里,
在直角三角形
中,,
所以
,
所以
,,
在直角三角形
中,,
所以
,
所以
,
解得
.
即该船行驶的速度为
海里
时.
三、解答题
13.
【答案】
.
14.
【答案】
(1)
如图,过点
作
于点
,作
.
,
由图得,,
在
中,
,,
,,
,
在
中,由勾股定理得:.
点
与点
的距离约为
.
(2)
在
中,
,,
,
,
.
点
位于点
的南偏东
方向.
15.
【答案】过点
作
于点
.
,,,
,.
,,
.
.
,
(米).
16.
【答案】
米
17.
【答案】
(1)
立方米;
(2)
.
18.
【答案】
小时.
19.
【答案】
(1)
的值为
.
作
轴,垂足为点
,
因为
,
所以
,
又因为
,
所以
.
(2)
斜边
在直角坐标系的
轴上有两种情况:
①点
在点
的右边(如图
).
因为
,,
所以
.
在
中,,,则
,
因为
,
所以
,即
.
从而
(或
),
所以点
的坐标为
(或写成
).
②点
在点
的左边(如图
),
同理可得点
的坐标为
(或写成
).
20.
【答案】
(1)
如图
.
,,
.
,
为等边三角形,则
,
,,
从而
,故
为等腰三角形.
与
相似,
为等腰三角形,,故
.
(2)
如图
.
设
,,
,解得
,则
.
过
作
交
于
,
,则
,即
,
从而
,同理可得
.
,则
,,从而解得
.
,
.
(3)
如图
.
当
时,设
,
.
由()知
,.
设
,则
,
,,.
,解得
(舍),.
.
