2020-2021学年八年级下册数学北京课改新版《第15章 四边形》单元测试题(word版含解析)
文档属性
| 名称 | 2020-2021学年八年级下册数学北京课改新版《第15章 四边形》单元测试题(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 199.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 00:00:00 | ||
图片预览



文档简介
2020-2021学年八年级下册数学北京课改新版《第15章
四边形》单元测试题
一.选择题
1.下列各组图形中,对角线互相平分且垂直的是( )
A.平行四边形与菱形
B.矩形与正方形
C.菱形与矩形
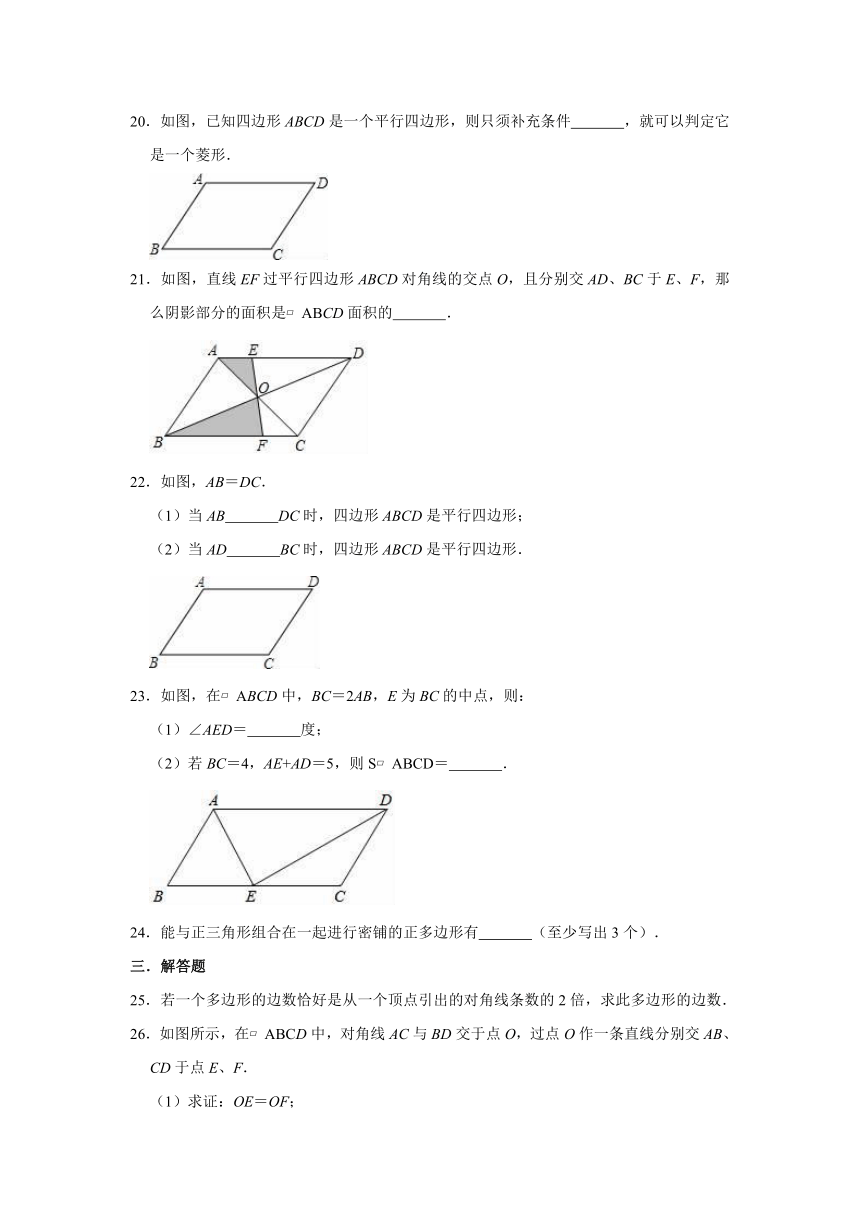
D.菱形与正方形
2.5名同学同台演出,在演出前,每两个同学握一次手,共握手的次数是( )
A.5次
B.10次
C.6次
D.8次
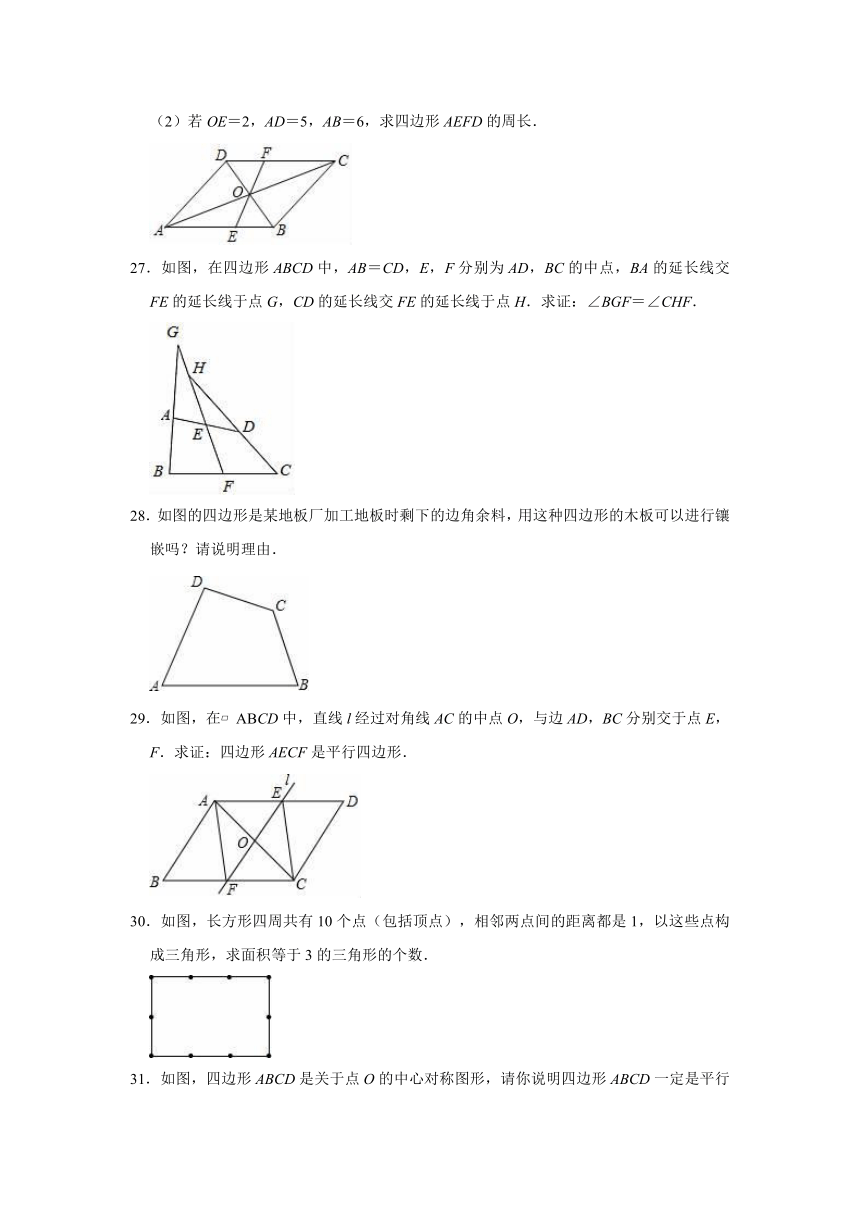
3.下列四个条件中,能判定四边形是平行四边形的是( )
A.一组对边平行,另一组对边相等
B.两条对角线互相垂直
C.两条对角线相等
D.一组对边平行,一组对角相等
4.用折纸、剪切的方法得到一个菱形,最少要剪( )刀(设一条线段剪一刀).
A.1
B.2
C.3
D.4
5.正方形的对角线长是18,则这个正方形的面积是( )
A.9
B.18
C.162
D.81
6.下列图形中既是中心对称图形,又是轴对称图形的是( )
A.角
B.等边三角形
C.正十二边形
D.正n边形
7.已知四边形ABCD中,∠A+∠B=180°,则下列结论中正确的是( )
A.AB∥CD
B.∠B+∠C=180°
C.∠B=∠C
D.∠C+∠D=180°
8.用正三角形和正十二边形镶嵌,可能情况有( )种.
A.1
B.2
C.3
D.4
9.矩形的面积为120cm2,周长为46cm,则它的对角线长为( )
A.15cm
B.16cm
C.17cm
D.18cm
10.已知平行四边形ABCD的两条对角线相交于直角坐标系的原点O,点A、B的坐标分别为(﹣1,3)、(1,2),则点C、D的坐标分别是( )
A.(1,﹣3),(﹣1,2)
B.(1,﹣3),(﹣1,﹣2)
C.(﹣1,﹣3),(﹣1,2)
D.(1,3),(﹣1,2)
11.如图,在四边形ABCD中,AB∥DC,M为DC的中点,N为AB的中点,则( )
A.MN>(AD+BC)
B.MN<(AD+BC)
C.MN=(AD+BC)
D.无法确定MN与(AD+BC)的关系
12.有两个内角分别为90°,60°,30°的完全一样的三角形拼成四边形,其形状不同的有( )
A.2个
B.3个
C.4个
D.6个
二.填空题
13.一个圆形绕一个定点旋转
,与初始图形
,这个图形叫做中心对称图形.
14.在图(1)中取阴影等边三角形各边的中点,连成一个等边三角形,将其挖去,得到图(2);对图(2)中的每个阴影等边三角形仿照先前的作法,得到图(3),如此继续.如果图(1)的等边三角形面积为1,则第n个图形中所有阴影三角形面积的和为
.
15.根据两条对角线的关系判断一个四边形是矩形或菱形或正方形的必不可少的条件是
.
16.桥梁拉杆,电视塔底座,都是三角形结构,这是利用三角形的
性;而活动挂架是四边形结构,这是利用四边形的
性.
17.如果一个多边形的边数增加1,它的内角和增加,那么这个多边形为
边形.
18.n边形过每一个顶点的对角线有
条.
19.把两根长度相等的木条的中点用螺栓固定在一起,依次连接木条的四个端点得到的四边形是
.
20.如图,已知四边形ABCD是一个平行四边形,则只须补充条件
,就可以判定它是一个菱形.
21.如图,直线EF过平行四边形ABCD对角线的交点O,且分别交AD、BC于E、F,那么阴影部分的面积是?ABCD面积的
.
22.如图,AB=DC.
(1)当AB
DC时,四边形ABCD是平行四边形;
(2)当AD
BC时,四边形ABCD是平行四边形.
23.如图,在?ABCD中,BC=2AB,E为BC的中点,则:
(1)∠AED=
度;
(2)若BC=4,AE+AD=5,则S?ABCD=
.
24.能与正三角形组合在一起进行密铺的正多边形有
(至少写出3个).
三.解答题
25.若一个多边形的边数恰好是从一个顶点引出的对角线条数的2倍,求此多边形的边数.
26.如图所示,在?ABCD中,对角线AC与BD交于点O,过点O作一条直线分别交AB、CD于点E、F.
(1)求证:OE=OF;
(2)若OE=2,AD=5,AB=6,求四边形AEFD的周长.
27.如图,在四边形ABCD中,AB=CD,E,F分别为AD,BC的中点,BA的延长线交FE的延长线于点G,CD的延长线交FE的延长线于点H.求证:∠BGF=∠CHF.
28.如图的四边形是某地板厂加工地板时剩下的边角余料,用这种四边形的木板可以进行镶嵌吗?请说明理由.
29.如图,在?ABCD中,直线l经过对角线AC的中点O,与边AD,BC分别交于点E,F.求证:四边形AECF是平行四边形.
30.如图,长方形四周共有10个点(包括顶点),相邻两点间的距离都是1,以这些点构成三角形,求面积等于3的三角形的个数.
31.如图,四边形ABCD是关于点O的中心对称图形,请你说明四边形ABCD一定是平行四边形.
参考答案与试题解析
一.选择题
1.解:A、不正确,平行四边形的对角线不互相垂直;
B、不正确,矩形的对角线不互相垂直;
C、不正确,矩形的对角线不互相垂直;
D、正确,两者的对角线均具有此性质;
故选:D.
2.解:有5名同学,因此每个人握手的次数为5×4=20次,
由于每两个人握手一次,所以它们握手的总次数为20÷2=10次.
故选:B.
3.解:一组对边平行,另一组对边相等A错;
任意的四边形的对角线也可能互相垂直,B错
两条对角线相等的也可能是等腰梯形,C错;
一组对角相等,一组对边平行.可得到任意两对邻角互补,那么可得到两组对边分别平行,为平行四边形.
故选:D.
4.解:一刀.将纸四折,把原来纸的中心作为直角三角形的直角,然后任意剪一个三角形下来,都是菱形.
故选:A.
5.解:菱形的面积计算公式:当对角线长度为a、b时,菱形面积S=ab;
正方形具有菱形的性质,所以该正方形面积S=×182==162.
故选:C.
6.解:A、是轴对称图形,不是中心对称图形,故本选项错误;
B、不是中心对称图形,是轴对称图形,故本选项错误;
C、既是中心对称图形又是轴对称图形,故本选项正确.
D、不是中心对称图形,是轴对称图形,故本选项错误;
故选:C.
7.解:∵四边形ABCD中,∠A+∠B=180°,
∴AD∥BC,
∴∠C+∠D=180°.
故选:D.
8.解:设用m块正三角形,n块正十二边形能镶嵌成平面.
由题意,有60m+150n=360,
解得m=6﹣n,
当n=2时,m=1.
故选:A.
9.解:设矩形长为a,宽为b.
∴ab=120;2(a+b)=46.
∴a2﹣23a+120=0.
∴a=15,b=8.
∴它的对角线的长为=17cm.
故选:C.
10.解:由题意知:点A与点C、点B与点D关于原点对称,
∵点A,B的坐标分别为(﹣1,3),(1,2),
∴点C,D的坐标分别是(1,﹣3),(﹣1,﹣2).
故选:B.
11.解:如图:连接BD,取BD的中点P,连接MP,NP,
∵M为DC的中点,N为AB的中点,点P是BD的中点,
∴MP=BC,NP=AD,
∵MN<MP+NP,
∴MN<
(AD+BC),
故选:B.
12.解:根据平行四边形的基本性质:平行四边形的两组对角分别相等,可知角分别为,(1)90°,90°,90°90°;(2)120°,60°,120°,60°;(3)150°,30°,150°,30°;不是平行四边形的四边形为(4)60°,90°,120°,90°.共4种,
故选:C.
二.填空题
13.解:一个图形绕一个定点旋转180°,与初始图形重合,这个图形叫做中心对称图形.
故答案为:180°,重合.
14.解:观察图形可以发现图(2)中留下的面积为图(1)的,
图(3)中留下的面积为图(2)的,
故新图形阴影部分的面积为原图形中阴影部分面积的,
∴第n个图形阴影部分的面积为,
故答案为.
15.解:∵矩形、菱形、正方形的对角线都具有平分的性质,
则根据两条对角线的关系判断一个四边形是矩形或菱形或正方形的必不可少的条件是平分.
故答案为平分.
16.解:桥梁拉杆,电视塔底座,都是三角形结构,这是利用三角形的稳定性;
而活动挂架是四边形结构,这是利用四边形的不稳定性.
17.解:设多边形的边数是n,根据题意得:180(n+1﹣2)=180(n﹣2)(1+),
解得:n=12.
故答案是:12.
18.解:n边形过每一个顶点的对角线有(n﹣3)条.
故答案为(n﹣3).
19.解:如图所示:
由题意得:AC=BD,O为AC和BD的中点,
∴OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
又∵AC=BD,
∴平行四边形ABCD是矩形;
故答案为:矩形.
20.解:补充的条件是AB=BC,
理由是:∵AB=BC,四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形,
故答案为:AB=BC.
21.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AO=CO,BO=DO,
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
∴S△ABD=S△CDB=S平行四边形ABCD,
∵BO=OD,
∴S△BOC=S△DOC=S△ABD=×S平行四边形ABCD=S平行四边形ABCD,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
在△AEO和△CFO中,
,
∴△AEO≌△CFO(ASA),
∴S△AEO=S△CFO,
∴阴影部分的面积S=S△AEO+S△BFO=S△CFO+S△BFO=S△BOC=S平行四边形ABCD,
故答案为:.
22.解:(1)当AB=DC,且AB∥DC时,四边形ABCD是平行四边形;
(2)当当AB=DC,且AD=BC时,四边形ABCD是平行四边形.
故答案是:∥;=.
23.解:(1)如图,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠2=∠3,∠4=∠6,
∵BC=2AB,E为BC的中点,
∴AB=BE,EC=DC,
∴∠1=∠3,∠4=∠5,
∴∠1=∠2,∠5=∠6,
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠1+∠2+∠5+∠6=180°,
∴∠2+∠6=90°,
∴∠AED=90°;
故答案为:90°;
(2)∵四边形ABCD是平行四边形,
∴AD=BC=4,
∵AE+AD=5,
∴AE=1,
∴ED==,
∴S△AED=AE?DE=,
∴S?ABCD=2S△AED=.
故答案为:.
24.解:正三角形的一个内角度数为180﹣360÷3=60°,正方形的一个内角度数为180﹣360÷4=90°,3×60+2×90=360°,∴3个正三角形和2个正方形可进行密铺;
正六边形的一个内角度数为180﹣360÷6=120°,2×60+2×120=360°或4×60+120=360°,可作平面镶嵌;
正十二边形的一个内角的度数为180﹣360÷12=150°,2×150+60=360°,可作平面镶嵌.
∴能与正三角形组合在一起进行密铺的正多边形有正方形,正六边形,正十二边形.
三.解答题
25.解:设此多边形有n条边,由题意,得
n=2(n﹣3),
解得n=6.
故此多边形有6条边.
26.(1)证明:在?ABCD中,
∵AC与BD相交于点O,
∴OA=OC,AB=CD,
∴∠OAE=∠OCF,
在△OAE和△OCF中,
,
∴△OAE≌△OCF(ASA),
∴OE=OF.
(2)解:∵△OAE≌△OCF,
∴CF=AE,
∴DF+AF=AB=6,
又∵EF=2OE=4,
∴四边形AEFD的周长=AD+DF+AE+EF=6+4+5=15.
27.证明:连接BD,取BD的中点M,连接EM、FM,
∵点E是AD的中点,
∴EM∥AB,EM=AB,
∴∠BGF=∠MEF,
同理可证:FM∥CD,FM=CD,
∴∠CHF=∠MFE,
∵AB=CD,
∴EM=FM,
∴∠MEF=∠MFE,
∴∠BGF=∠CHF.
28.解:能进行镶嵌;
理由:由镶嵌的条件知,在一个顶点处各个内角的和为360°时,就能镶嵌.
而任意四边形的内角和是360°,只要放在同一顶点的4个内角和为360°,
故能进行镶嵌.
29.证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴AE∥CF,
∴∠OAE=∠OCF,
∵点O是AC的中点,
∴OA=OC,
又∵∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴AE=CF,
∵AE∥CF,
∴四边形AECF是平行四边形.
30.解:如图,
符合底为3,高为2的有8个,
分别是:△AMF,△DFM,△AMD,△AFD,△MBF,△MCF,△AHD,△AGD;
符合底为2,高为3的有2个,
分别是:△AEM,△DNF.
即面积等于3的三角形的个数有10个.
31.解:连接AC、BD,
∵四边形ABCD是关于点O的中心对称图形,
则AC和BD都经过点O,且OA=OC,OB=OD,
所以四边形ABCD为平行四边形.
四边形》单元测试题
一.选择题
1.下列各组图形中,对角线互相平分且垂直的是( )
A.平行四边形与菱形
B.矩形与正方形
C.菱形与矩形
D.菱形与正方形
2.5名同学同台演出,在演出前,每两个同学握一次手,共握手的次数是( )
A.5次
B.10次
C.6次
D.8次
3.下列四个条件中,能判定四边形是平行四边形的是( )
A.一组对边平行,另一组对边相等
B.两条对角线互相垂直
C.两条对角线相等
D.一组对边平行,一组对角相等
4.用折纸、剪切的方法得到一个菱形,最少要剪( )刀(设一条线段剪一刀).
A.1
B.2
C.3
D.4
5.正方形的对角线长是18,则这个正方形的面积是( )
A.9
B.18
C.162
D.81
6.下列图形中既是中心对称图形,又是轴对称图形的是( )
A.角
B.等边三角形
C.正十二边形
D.正n边形
7.已知四边形ABCD中,∠A+∠B=180°,则下列结论中正确的是( )
A.AB∥CD
B.∠B+∠C=180°
C.∠B=∠C
D.∠C+∠D=180°
8.用正三角形和正十二边形镶嵌,可能情况有( )种.
A.1
B.2
C.3
D.4
9.矩形的面积为120cm2,周长为46cm,则它的对角线长为( )
A.15cm
B.16cm
C.17cm
D.18cm
10.已知平行四边形ABCD的两条对角线相交于直角坐标系的原点O,点A、B的坐标分别为(﹣1,3)、(1,2),则点C、D的坐标分别是( )
A.(1,﹣3),(﹣1,2)
B.(1,﹣3),(﹣1,﹣2)
C.(﹣1,﹣3),(﹣1,2)
D.(1,3),(﹣1,2)
11.如图,在四边形ABCD中,AB∥DC,M为DC的中点,N为AB的中点,则( )
A.MN>(AD+BC)
B.MN<(AD+BC)
C.MN=(AD+BC)
D.无法确定MN与(AD+BC)的关系
12.有两个内角分别为90°,60°,30°的完全一样的三角形拼成四边形,其形状不同的有( )
A.2个
B.3个
C.4个
D.6个
二.填空题
13.一个圆形绕一个定点旋转
,与初始图形
,这个图形叫做中心对称图形.
14.在图(1)中取阴影等边三角形各边的中点,连成一个等边三角形,将其挖去,得到图(2);对图(2)中的每个阴影等边三角形仿照先前的作法,得到图(3),如此继续.如果图(1)的等边三角形面积为1,则第n个图形中所有阴影三角形面积的和为
.
15.根据两条对角线的关系判断一个四边形是矩形或菱形或正方形的必不可少的条件是
.
16.桥梁拉杆,电视塔底座,都是三角形结构,这是利用三角形的
性;而活动挂架是四边形结构,这是利用四边形的
性.
17.如果一个多边形的边数增加1,它的内角和增加,那么这个多边形为
边形.
18.n边形过每一个顶点的对角线有
条.
19.把两根长度相等的木条的中点用螺栓固定在一起,依次连接木条的四个端点得到的四边形是
.
20.如图,已知四边形ABCD是一个平行四边形,则只须补充条件
,就可以判定它是一个菱形.
21.如图,直线EF过平行四边形ABCD对角线的交点O,且分别交AD、BC于E、F,那么阴影部分的面积是?ABCD面积的
.
22.如图,AB=DC.
(1)当AB
DC时,四边形ABCD是平行四边形;
(2)当AD
BC时,四边形ABCD是平行四边形.
23.如图,在?ABCD中,BC=2AB,E为BC的中点,则:
(1)∠AED=
度;
(2)若BC=4,AE+AD=5,则S?ABCD=
.
24.能与正三角形组合在一起进行密铺的正多边形有
(至少写出3个).
三.解答题
25.若一个多边形的边数恰好是从一个顶点引出的对角线条数的2倍,求此多边形的边数.
26.如图所示,在?ABCD中,对角线AC与BD交于点O,过点O作一条直线分别交AB、CD于点E、F.
(1)求证:OE=OF;
(2)若OE=2,AD=5,AB=6,求四边形AEFD的周长.
27.如图,在四边形ABCD中,AB=CD,E,F分别为AD,BC的中点,BA的延长线交FE的延长线于点G,CD的延长线交FE的延长线于点H.求证:∠BGF=∠CHF.
28.如图的四边形是某地板厂加工地板时剩下的边角余料,用这种四边形的木板可以进行镶嵌吗?请说明理由.
29.如图,在?ABCD中,直线l经过对角线AC的中点O,与边AD,BC分别交于点E,F.求证:四边形AECF是平行四边形.
30.如图,长方形四周共有10个点(包括顶点),相邻两点间的距离都是1,以这些点构成三角形,求面积等于3的三角形的个数.
31.如图,四边形ABCD是关于点O的中心对称图形,请你说明四边形ABCD一定是平行四边形.
参考答案与试题解析
一.选择题
1.解:A、不正确,平行四边形的对角线不互相垂直;
B、不正确,矩形的对角线不互相垂直;
C、不正确,矩形的对角线不互相垂直;
D、正确,两者的对角线均具有此性质;
故选:D.
2.解:有5名同学,因此每个人握手的次数为5×4=20次,
由于每两个人握手一次,所以它们握手的总次数为20÷2=10次.
故选:B.
3.解:一组对边平行,另一组对边相等A错;
任意的四边形的对角线也可能互相垂直,B错
两条对角线相等的也可能是等腰梯形,C错;
一组对角相等,一组对边平行.可得到任意两对邻角互补,那么可得到两组对边分别平行,为平行四边形.
故选:D.
4.解:一刀.将纸四折,把原来纸的中心作为直角三角形的直角,然后任意剪一个三角形下来,都是菱形.
故选:A.
5.解:菱形的面积计算公式:当对角线长度为a、b时,菱形面积S=ab;
正方形具有菱形的性质,所以该正方形面积S=×182==162.
故选:C.
6.解:A、是轴对称图形,不是中心对称图形,故本选项错误;
B、不是中心对称图形,是轴对称图形,故本选项错误;
C、既是中心对称图形又是轴对称图形,故本选项正确.
D、不是中心对称图形,是轴对称图形,故本选项错误;
故选:C.
7.解:∵四边形ABCD中,∠A+∠B=180°,
∴AD∥BC,
∴∠C+∠D=180°.
故选:D.
8.解:设用m块正三角形,n块正十二边形能镶嵌成平面.
由题意,有60m+150n=360,
解得m=6﹣n,
当n=2时,m=1.
故选:A.
9.解:设矩形长为a,宽为b.
∴ab=120;2(a+b)=46.
∴a2﹣23a+120=0.
∴a=15,b=8.
∴它的对角线的长为=17cm.
故选:C.
10.解:由题意知:点A与点C、点B与点D关于原点对称,
∵点A,B的坐标分别为(﹣1,3),(1,2),
∴点C,D的坐标分别是(1,﹣3),(﹣1,﹣2).
故选:B.
11.解:如图:连接BD,取BD的中点P,连接MP,NP,
∵M为DC的中点,N为AB的中点,点P是BD的中点,
∴MP=BC,NP=AD,
∵MN<MP+NP,
∴MN<
(AD+BC),
故选:B.
12.解:根据平行四边形的基本性质:平行四边形的两组对角分别相等,可知角分别为,(1)90°,90°,90°90°;(2)120°,60°,120°,60°;(3)150°,30°,150°,30°;不是平行四边形的四边形为(4)60°,90°,120°,90°.共4种,
故选:C.
二.填空题
13.解:一个图形绕一个定点旋转180°,与初始图形重合,这个图形叫做中心对称图形.
故答案为:180°,重合.
14.解:观察图形可以发现图(2)中留下的面积为图(1)的,
图(3)中留下的面积为图(2)的,
故新图形阴影部分的面积为原图形中阴影部分面积的,
∴第n个图形阴影部分的面积为,
故答案为.
15.解:∵矩形、菱形、正方形的对角线都具有平分的性质,
则根据两条对角线的关系判断一个四边形是矩形或菱形或正方形的必不可少的条件是平分.
故答案为平分.
16.解:桥梁拉杆,电视塔底座,都是三角形结构,这是利用三角形的稳定性;
而活动挂架是四边形结构,这是利用四边形的不稳定性.
17.解:设多边形的边数是n,根据题意得:180(n+1﹣2)=180(n﹣2)(1+),
解得:n=12.
故答案是:12.
18.解:n边形过每一个顶点的对角线有(n﹣3)条.
故答案为(n﹣3).
19.解:如图所示:
由题意得:AC=BD,O为AC和BD的中点,
∴OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
又∵AC=BD,
∴平行四边形ABCD是矩形;
故答案为:矩形.
20.解:补充的条件是AB=BC,
理由是:∵AB=BC,四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形,
故答案为:AB=BC.
21.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AO=CO,BO=DO,
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
∴S△ABD=S△CDB=S平行四边形ABCD,
∵BO=OD,
∴S△BOC=S△DOC=S△ABD=×S平行四边形ABCD=S平行四边形ABCD,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
在△AEO和△CFO中,
,
∴△AEO≌△CFO(ASA),
∴S△AEO=S△CFO,
∴阴影部分的面积S=S△AEO+S△BFO=S△CFO+S△BFO=S△BOC=S平行四边形ABCD,
故答案为:.
22.解:(1)当AB=DC,且AB∥DC时,四边形ABCD是平行四边形;
(2)当当AB=DC,且AD=BC时,四边形ABCD是平行四边形.
故答案是:∥;=.
23.解:(1)如图,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠2=∠3,∠4=∠6,
∵BC=2AB,E为BC的中点,
∴AB=BE,EC=DC,
∴∠1=∠3,∠4=∠5,
∴∠1=∠2,∠5=∠6,
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠1+∠2+∠5+∠6=180°,
∴∠2+∠6=90°,
∴∠AED=90°;
故答案为:90°;
(2)∵四边形ABCD是平行四边形,
∴AD=BC=4,
∵AE+AD=5,
∴AE=1,
∴ED==,
∴S△AED=AE?DE=,
∴S?ABCD=2S△AED=.
故答案为:.
24.解:正三角形的一个内角度数为180﹣360÷3=60°,正方形的一个内角度数为180﹣360÷4=90°,3×60+2×90=360°,∴3个正三角形和2个正方形可进行密铺;
正六边形的一个内角度数为180﹣360÷6=120°,2×60+2×120=360°或4×60+120=360°,可作平面镶嵌;
正十二边形的一个内角的度数为180﹣360÷12=150°,2×150+60=360°,可作平面镶嵌.
∴能与正三角形组合在一起进行密铺的正多边形有正方形,正六边形,正十二边形.
三.解答题
25.解:设此多边形有n条边,由题意,得
n=2(n﹣3),
解得n=6.
故此多边形有6条边.
26.(1)证明:在?ABCD中,
∵AC与BD相交于点O,
∴OA=OC,AB=CD,
∴∠OAE=∠OCF,
在△OAE和△OCF中,
,
∴△OAE≌△OCF(ASA),
∴OE=OF.
(2)解:∵△OAE≌△OCF,
∴CF=AE,
∴DF+AF=AB=6,
又∵EF=2OE=4,
∴四边形AEFD的周长=AD+DF+AE+EF=6+4+5=15.
27.证明:连接BD,取BD的中点M,连接EM、FM,
∵点E是AD的中点,
∴EM∥AB,EM=AB,
∴∠BGF=∠MEF,
同理可证:FM∥CD,FM=CD,
∴∠CHF=∠MFE,
∵AB=CD,
∴EM=FM,
∴∠MEF=∠MFE,
∴∠BGF=∠CHF.
28.解:能进行镶嵌;
理由:由镶嵌的条件知,在一个顶点处各个内角的和为360°时,就能镶嵌.
而任意四边形的内角和是360°,只要放在同一顶点的4个内角和为360°,
故能进行镶嵌.
29.证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴AE∥CF,
∴∠OAE=∠OCF,
∵点O是AC的中点,
∴OA=OC,
又∵∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴AE=CF,
∵AE∥CF,
∴四边形AECF是平行四边形.
30.解:如图,
符合底为3,高为2的有8个,
分别是:△AMF,△DFM,△AMD,△AFD,△MBF,△MCF,△AHD,△AGD;
符合底为2,高为3的有2个,
分别是:△AEM,△DNF.
即面积等于3的三角形的个数有10个.
31.解:连接AC、BD,
∵四边形ABCD是关于点O的中心对称图形,
则AC和BD都经过点O,且OA=OC,OB=OD,
所以四边形ABCD为平行四边形.
同课章节目录
