2020-2021学年冀教版八年级数学下册第二十一章一次函数综合专题(word版无答案)
文档属性
| 名称 | 2020-2021学年冀教版八年级数学下册第二十一章一次函数综合专题(word版无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 113.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 15:57:27 | ||
图片预览

文档简介
八年级第二学期一次函数综合专题提升
1.一次函数y=-2x-1的图像大致是( )
2.已知点(-1,y1),(4,y2)在一次函数y=3x-2的图像上,则y1,y2,0的大小关系是( )
A.0<y1<y2
B.y1<0<y2
C.y1<y2<0
D.y2<0<y1
3.如图,△ABC中,已知BC=16,高AD=10,动点Q由C点沿CB向B点移动(不与点B重合).设CQ长为x,△ACQ的面积为S,则S与x之间的函数关系式为( )
A.S=80-5x
B.S=5x
C.S=10x
D.S=5x+80
第3题图
第4题图
4.如图,若点P(-2,4)关于y轴的对称点在一次函数y=x+b的图像上,则b的值为( )
A.-2
B.2
C.-6
D.6
5.已知一次函数y=x+和y=-x-1的图像都经过点A,且与y轴分别交于B,C两点,那么△ABC的面积是( )
A.2
B.3
C.
D.6
6.甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人乘车前往目的地所行驶的路程s(千米)随时间t(分钟)变化的函数图像如图所示,则每分钟乙所乘的车比甲所乘的车多行驶的路程是( )
A.0.5千米
B.1千米
C.1.5千米
D.2千米
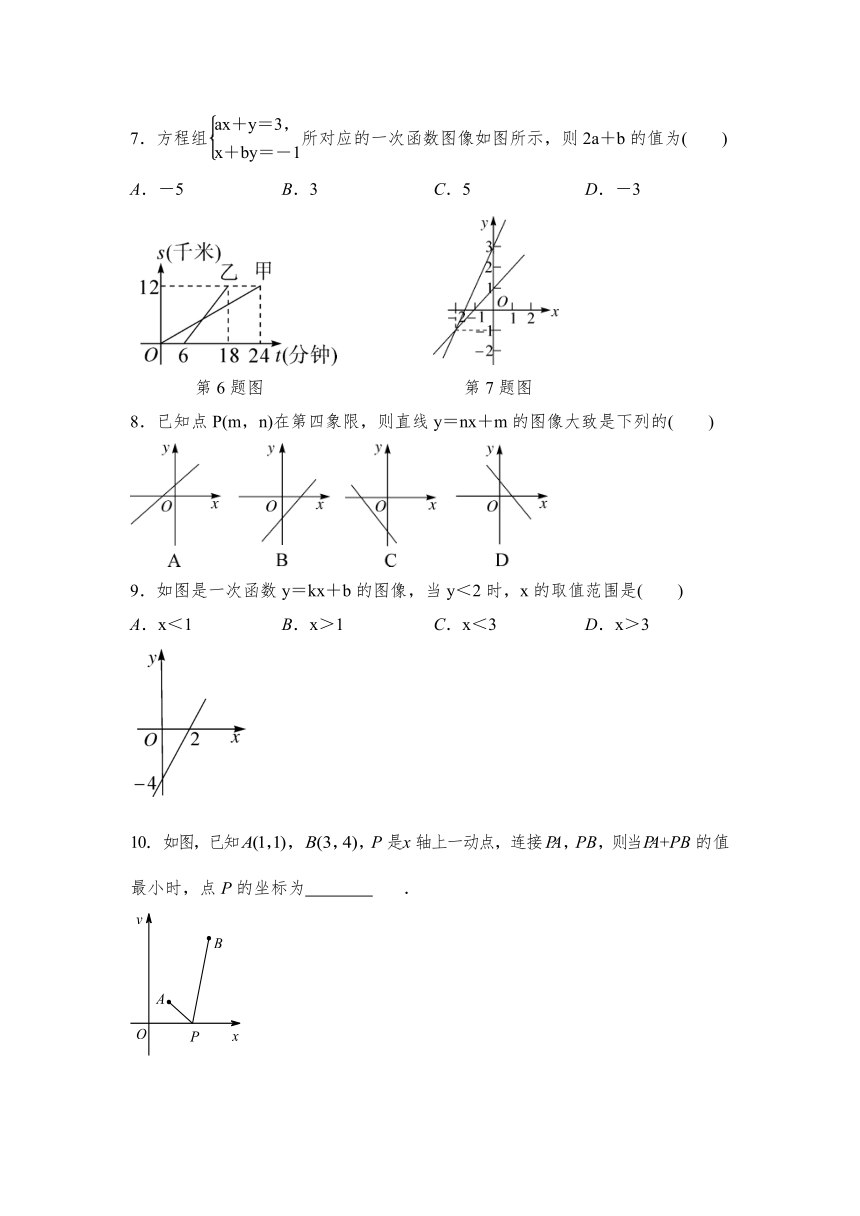
7.方程组所对应的一次函数图像如图所示,则2a+b的值为( )
A.-5
B.3
C.5
D.-3
第6题图
第7题图
8.已知点P(m,n)在第四象限,则直线y=nx+m的图像大致是下列的( )
9.如图是一次函数y=kx+b的图像,当y<2时,x的取值范围是( )
A.x<1
B.x>1
C.x<3
D.x>3
10.如图,已知A(1,1),B(3,4),P是x轴上一动点,连接PA,PB,则当PA+PB的值最小时,点P的坐标为
.
11.若点A(m,n)在直线y=kx(k≠0)上,当-1≤m≤1时,-1≤n≤1,则这条直线的函数表达式为________________.
12.如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上.若△A1OB1,△A2B1B2,△A3B2B3,…依次均为等腰直角三角形,直角顶点都在x轴上,则第2017个等腰直角三角形A2017B2016B2017顶点B2017的横坐标为________.
13.如图,已知函数y=ax+b和y=kx的图像交于点P,则根据图像可得关于x,y的二元一次方程组的解是______________.
第13题图
第14题图
14.如图,折线ABC是甲地向乙地打国际长途电话所需付的电话费y(元)与通话时间t(分钟)之间的函数关系的图像,当t≥3时,表达式是______________;通话2分钟,需付费________元;通话7分钟,需付费________元.
15.大拇指与小拇指尽量张开时,两指尖的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:
指距d(cm)
20
21
22
23
身高h(cm)
160
169
178
187
(1)求出h与d之间的函数关系式(不要求写出自变量d的取值范围);
(2)某人身高为196cm,一般情况下他的指距应是多少?
16.如图,正比例函数y=2x的图像与一次函数y=kx+b的图像交于点A(m,2),一次函数的图像经过点B(-2,-1),与y轴的交点为C,与x轴的交点为D.
(1)求一次函数的表达式;
(2)求C点的坐标;
(3)求△AOD的面积.
17.为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员支付两种支付方式,下图描述了两种方式的支付金额y(元)与骑行时间x(小时)之间的函数关系,根据图像回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(小时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.
1.一次函数y=-2x-1的图像大致是( )
2.已知点(-1,y1),(4,y2)在一次函数y=3x-2的图像上,则y1,y2,0的大小关系是( )
A.0<y1<y2
B.y1<0<y2
C.y1<y2<0
D.y2<0<y1
3.如图,△ABC中,已知BC=16,高AD=10,动点Q由C点沿CB向B点移动(不与点B重合).设CQ长为x,△ACQ的面积为S,则S与x之间的函数关系式为( )
A.S=80-5x
B.S=5x
C.S=10x
D.S=5x+80
第3题图
第4题图
4.如图,若点P(-2,4)关于y轴的对称点在一次函数y=x+b的图像上,则b的值为( )
A.-2
B.2
C.-6
D.6
5.已知一次函数y=x+和y=-x-1的图像都经过点A,且与y轴分别交于B,C两点,那么△ABC的面积是( )
A.2
B.3
C.
D.6
6.甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人乘车前往目的地所行驶的路程s(千米)随时间t(分钟)变化的函数图像如图所示,则每分钟乙所乘的车比甲所乘的车多行驶的路程是( )
A.0.5千米
B.1千米
C.1.5千米
D.2千米
7.方程组所对应的一次函数图像如图所示,则2a+b的值为( )
A.-5
B.3
C.5
D.-3
第6题图
第7题图
8.已知点P(m,n)在第四象限,则直线y=nx+m的图像大致是下列的( )
9.如图是一次函数y=kx+b的图像,当y<2时,x的取值范围是( )
A.x<1
B.x>1
C.x<3
D.x>3
10.如图,已知A(1,1),B(3,4),P是x轴上一动点,连接PA,PB,则当PA+PB的值最小时,点P的坐标为
.
11.若点A(m,n)在直线y=kx(k≠0)上,当-1≤m≤1时,-1≤n≤1,则这条直线的函数表达式为________________.
12.如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上.若△A1OB1,△A2B1B2,△A3B2B3,…依次均为等腰直角三角形,直角顶点都在x轴上,则第2017个等腰直角三角形A2017B2016B2017顶点B2017的横坐标为________.
13.如图,已知函数y=ax+b和y=kx的图像交于点P,则根据图像可得关于x,y的二元一次方程组的解是______________.
第13题图
第14题图
14.如图,折线ABC是甲地向乙地打国际长途电话所需付的电话费y(元)与通话时间t(分钟)之间的函数关系的图像,当t≥3时,表达式是______________;通话2分钟,需付费________元;通话7分钟,需付费________元.
15.大拇指与小拇指尽量张开时,两指尖的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:
指距d(cm)
20
21
22
23
身高h(cm)
160
169
178
187
(1)求出h与d之间的函数关系式(不要求写出自变量d的取值范围);
(2)某人身高为196cm,一般情况下他的指距应是多少?
16.如图,正比例函数y=2x的图像与一次函数y=kx+b的图像交于点A(m,2),一次函数的图像经过点B(-2,-1),与y轴的交点为C,与x轴的交点为D.
(1)求一次函数的表达式;
(2)求C点的坐标;
(3)求△AOD的面积.
17.为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员支付两种支付方式,下图描述了两种方式的支付金额y(元)与骑行时间x(小时)之间的函数关系,根据图像回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(小时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
