2020-2021学年北师大版数学(重庆专用)七年级下册 第二章 1两条直线的位置关系 演练提升(含2课时,word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版数学(重庆专用)七年级下册 第二章 1两条直线的位置关系 演练提升(含2课时,word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 184.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 23:21:52 | ||
图片预览


文档简介
第二章 相交线与平行线
1 两条直线的位置关系
第1课时
知能演练提升
能力提升
1.a,b,c是平面内任意三条直线,交点可以有( )
A.1个或2个或3个
B.0个或1个或2个或3个
C.1个或2个
D.都不对
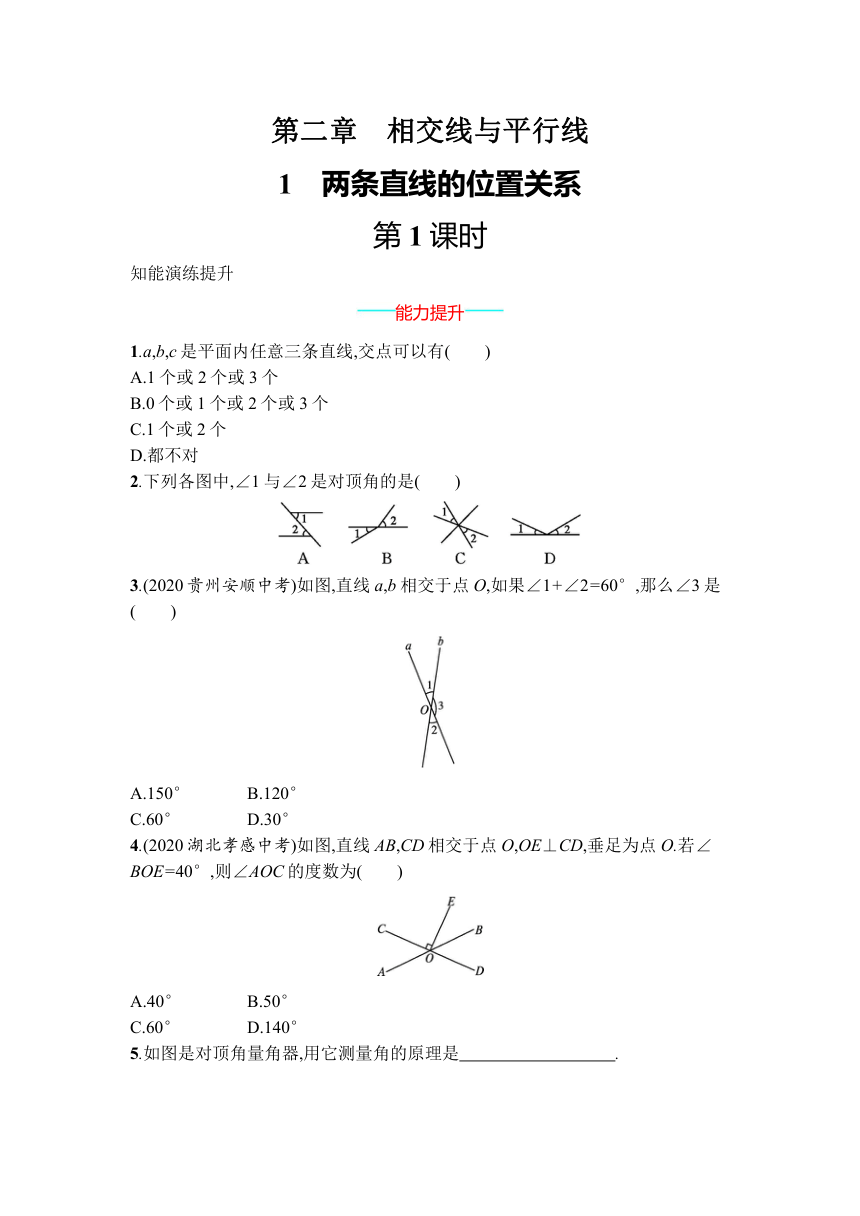
2.下列各图中,∠1与∠2是对顶角的是( )
3.(2020贵州安顺中考)如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3是( )
A.150°
B.120°
C.60°
D.30°
4.(2020湖北孝感中考)如图,直线AB,CD相交于点O,OE⊥CD,垂足为点O.若∠BOE=40°,则∠AOC的度数为( )
A.40°
B.50°
C.60°
D.140°
5.如图是对顶角量角器,用它测量角的原理是? .?
6.下列说法正确的有 .(只填序号)?
①钝角与锐角互补;②∠α的余角是90°-∠α;③∠β的补角是180°-∠β(0°<∠β<180°);④若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余.
7.如图,直线AB与CD相交于点O,OE平分∠AOD,∠AOC=120°,求∠BOD,∠AOE的度数.
创新应用
8.如图,这是一个经过改造的台球桌面的示意图,图中4个角上的阴影部分分别表示4个入球袋.如果一个球按图中所示的方向被击出(假设用足够的力气击出,使球可以经过多次反射),那么该球最后落入哪个球袋?在图上画出被击的球所走路线.
第2课时
知能演练提升
能力提升
1.如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
A.两点之间线段最短
B.点到直线的距离
C.两点确定一条直线
D.垂线段最短
2.如图,在线段PA,PB,PC,PD中,长度最小的是( )
A.线段PA
B.线段PB
C.线段PC
D.线段PD
3.已知A,B,C,D是直线l上的四点,点P是直线l外一点,且PA=5
cm,PB=4
cm,PC=3
cm,PD=2
cm,则点P到直线l的距离( )
A.等于2
cm
B.等于3
cm
C.不大于2
cm
D.小于2
cm
4.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是 .?
5.如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,则图中线段的长度可以作为点到直线的距离的一共有 条.?
6.如图,AB⊥CD于点C,CE⊥CF于点C,则图中共有 对互余的角.?
7.如图,P是直线AB上一点,∠APC=∠BPC,∠CPD=2∠APC.
(1)求∠CPD的度数;
(2)判断PD与AB的位置关系,并说明理由.
创新应用
8.如图,先找到长方形纸的宽DC的中点E,将∠C过点E折起任意一个角,折痕是EF,再将∠D过点E折起,使D'E和C'E重合,折痕是GE,请探索下列问题:
(1)∠FEC'和∠GEC'互为余角吗?为什么?
(2)∠GEF是直角吗?为什么?
(3)在上述折纸图形中,还有哪些角互为余角?还有哪些角互为补角(各写出两对)?
第1课时
答案:
能力提升
1.B 2.C 3.A 4.B
5.对顶角相等 6.③
7.解:因为直线AB与CD相交于点O,∠AOC=120°,
所以∠BOD=∠AOC=120°(对顶角相等).
因为∠AOC+∠AOD=180°,
所以∠AOD=180°-120°=60°.
又因为OE平分∠AOD,
所以∠AOE=∠AOD=×60°=30°(角平分线定义).
创新应用
8.分析
此题应与实际相联系,球被击中后在桌面上走的路线与台球桌面的边缘构成的角等于反弹后走的路线与台球桌面的边缘构成的角.
解:落入2号球袋,如图.
第2课时
答案:
能力提升
1.D 2.B 3.C 4.60°或120° 5.5 6.4
7.解:(1)因为平角∠APB=180°,∠APC=∠BPC,所以∠APC=180°÷6=30°,所以∠CPD=2∠APC=60°.
(2)PD⊥AB.理由如下:
因为∠APD=∠APC+∠CPD=30°+60°=90°,即∠APD是直角,所以PD⊥AB.
创新应用
8.解:(1)∠FEC'和∠GEC'互为余角.理由如下:
由折纸试验,知∠3=∠1,∠4=∠2,而∠1+∠2+∠3+∠4=180°,所以∠1+∠2=90°,
即∠FEC'+∠GEC'=90°.
故∠FEC'和∠GEC'互为余角.
(2)∠GEF是直角.理由如下:因为∠GEF=∠1+∠2=90°,所以∠GEF是直角.
(3)∠3和∠4,∠1和∠EFG互为余角,∠AGF和∠DGF,∠CEC'和∠DEC'互为补角.(答案不唯一)
1 两条直线的位置关系
第1课时
知能演练提升
能力提升
1.a,b,c是平面内任意三条直线,交点可以有( )
A.1个或2个或3个
B.0个或1个或2个或3个
C.1个或2个
D.都不对
2.下列各图中,∠1与∠2是对顶角的是( )
3.(2020贵州安顺中考)如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3是( )
A.150°
B.120°
C.60°
D.30°
4.(2020湖北孝感中考)如图,直线AB,CD相交于点O,OE⊥CD,垂足为点O.若∠BOE=40°,则∠AOC的度数为( )
A.40°
B.50°
C.60°
D.140°
5.如图是对顶角量角器,用它测量角的原理是? .?
6.下列说法正确的有 .(只填序号)?
①钝角与锐角互补;②∠α的余角是90°-∠α;③∠β的补角是180°-∠β(0°<∠β<180°);④若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余.
7.如图,直线AB与CD相交于点O,OE平分∠AOD,∠AOC=120°,求∠BOD,∠AOE的度数.
创新应用
8.如图,这是一个经过改造的台球桌面的示意图,图中4个角上的阴影部分分别表示4个入球袋.如果一个球按图中所示的方向被击出(假设用足够的力气击出,使球可以经过多次反射),那么该球最后落入哪个球袋?在图上画出被击的球所走路线.
第2课时
知能演练提升
能力提升
1.如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
A.两点之间线段最短
B.点到直线的距离
C.两点确定一条直线
D.垂线段最短
2.如图,在线段PA,PB,PC,PD中,长度最小的是( )
A.线段PA
B.线段PB
C.线段PC
D.线段PD
3.已知A,B,C,D是直线l上的四点,点P是直线l外一点,且PA=5
cm,PB=4
cm,PC=3
cm,PD=2
cm,则点P到直线l的距离( )
A.等于2
cm
B.等于3
cm
C.不大于2
cm
D.小于2
cm
4.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是 .?
5.如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,则图中线段的长度可以作为点到直线的距离的一共有 条.?
6.如图,AB⊥CD于点C,CE⊥CF于点C,则图中共有 对互余的角.?
7.如图,P是直线AB上一点,∠APC=∠BPC,∠CPD=2∠APC.
(1)求∠CPD的度数;
(2)判断PD与AB的位置关系,并说明理由.
创新应用
8.如图,先找到长方形纸的宽DC的中点E,将∠C过点E折起任意一个角,折痕是EF,再将∠D过点E折起,使D'E和C'E重合,折痕是GE,请探索下列问题:
(1)∠FEC'和∠GEC'互为余角吗?为什么?
(2)∠GEF是直角吗?为什么?
(3)在上述折纸图形中,还有哪些角互为余角?还有哪些角互为补角(各写出两对)?
第1课时
答案:
能力提升
1.B 2.C 3.A 4.B
5.对顶角相等 6.③
7.解:因为直线AB与CD相交于点O,∠AOC=120°,
所以∠BOD=∠AOC=120°(对顶角相等).
因为∠AOC+∠AOD=180°,
所以∠AOD=180°-120°=60°.
又因为OE平分∠AOD,
所以∠AOE=∠AOD=×60°=30°(角平分线定义).
创新应用
8.分析
此题应与实际相联系,球被击中后在桌面上走的路线与台球桌面的边缘构成的角等于反弹后走的路线与台球桌面的边缘构成的角.
解:落入2号球袋,如图.
第2课时
答案:
能力提升
1.D 2.B 3.C 4.60°或120° 5.5 6.4
7.解:(1)因为平角∠APB=180°,∠APC=∠BPC,所以∠APC=180°÷6=30°,所以∠CPD=2∠APC=60°.
(2)PD⊥AB.理由如下:
因为∠APD=∠APC+∠CPD=30°+60°=90°,即∠APD是直角,所以PD⊥AB.
创新应用
8.解:(1)∠FEC'和∠GEC'互为余角.理由如下:
由折纸试验,知∠3=∠1,∠4=∠2,而∠1+∠2+∠3+∠4=180°,所以∠1+∠2=90°,
即∠FEC'+∠GEC'=90°.
故∠FEC'和∠GEC'互为余角.
(2)∠GEF是直角.理由如下:因为∠GEF=∠1+∠2=90°,所以∠GEF是直角.
(3)∠3和∠4,∠1和∠EFG互为余角,∠AGF和∠DGF,∠CEC'和∠DEC'互为补角.(答案不唯一)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
