9.2 中心对称与中心对称图形同步训练(含解析)
文档属性
| 名称 | 9.2 中心对称与中心对称图形同步训练(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
初中数学苏科版八年级下册
9.2
中心对称与中心对称图形
同步训练
一、单选题(本题共10题,每题3分,共30分)
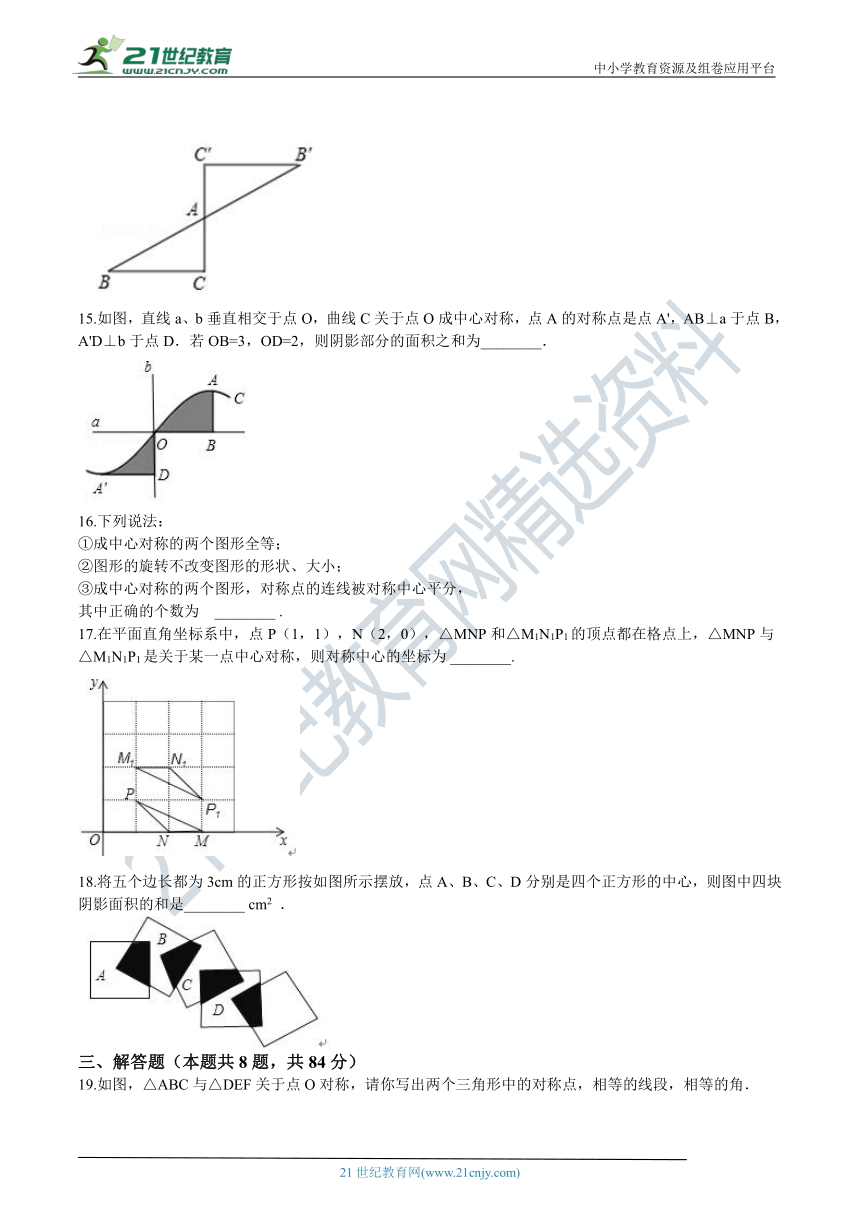
1.下列图形中,是中心对称图形但不是轴对称图形的是(??
)
A.?????????????????????B.?????????????????????C.?????????????????????D.?
2.在正三角形、等腰梯形、矩形和圆这四种图形中,既是轴对称图形又是中心对称图形的有( )种.
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
3.下列说法正确的是(??
)
A.?全等的两个图形成中心对称????????????????????????????????B.?成中心对称的两个图形必须重合
C.?成中心对称的两个图形全等????????????????????????????????D.?旋转后能够重合的两个图形成中心对称
4.如图,已知图形是中心对称图形,则对称中心是(???
)
A.?点C????????????????????????????B.?点D????????????????????????????C.?线段BC的中点????????????????????????????D.?线段FC的中点
5.已知四边形ABCD与四边形A′B′C′D′关于点O成中心对称,则AB与A′B′的关系是(??
)
A.?相等???????????????B.?垂直???????????????C.?相等并且平行???????????????D.?相等并且平行或相等并且在同一直线上
6.如图,四边形ABD与四边形FGHE关于一个点成中心对称,则这个点是(??
)
A.?O1????????????????????????????????????????B.?O2????????????????????????????????????????C.?O3????????????????????????????????????????D.?O4
7.已知△ABC和△DEF关于点O对称,相应的对称点如图所示,则下列结论正确的是(??
)
A.?AO=BO????????????B.?BO=EO????????????C.?点A关于点O的对称点是点D????????????D.?点D
在BO的延长线上
8.如图,在方格纸中,选择标有序号①②③④的小正方形中的一个涂黑,
与图中阴影部分构成中心对称图形,则该小正方形的序号是(??
)
A.?①?????????????????????????????????????????B.?②?????????????????????????????????????????C.?③?????????????????????????????????????????D.?④
9.四张扑克牌如图①所示放在桌面上,小敏把其中一张旋转180°后得到图②,则她所旋转的牌从左数起是(??
)
A.?第一张????????????????????????????????B.?第二张????????????????????????????????C.?第三张????????????????????????????????D.?第四张
10.若两个图形成中心对称,则下列说法:①对应点的连线必经过对称中心;②这两个图形的形状大小完全相同;③这两个图形的对应线段一定相等;④将一个图形绕对称中心旋转180°后必与另一个图形重合.正确的有(???
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题(本题共8题,每题2分,共16分)
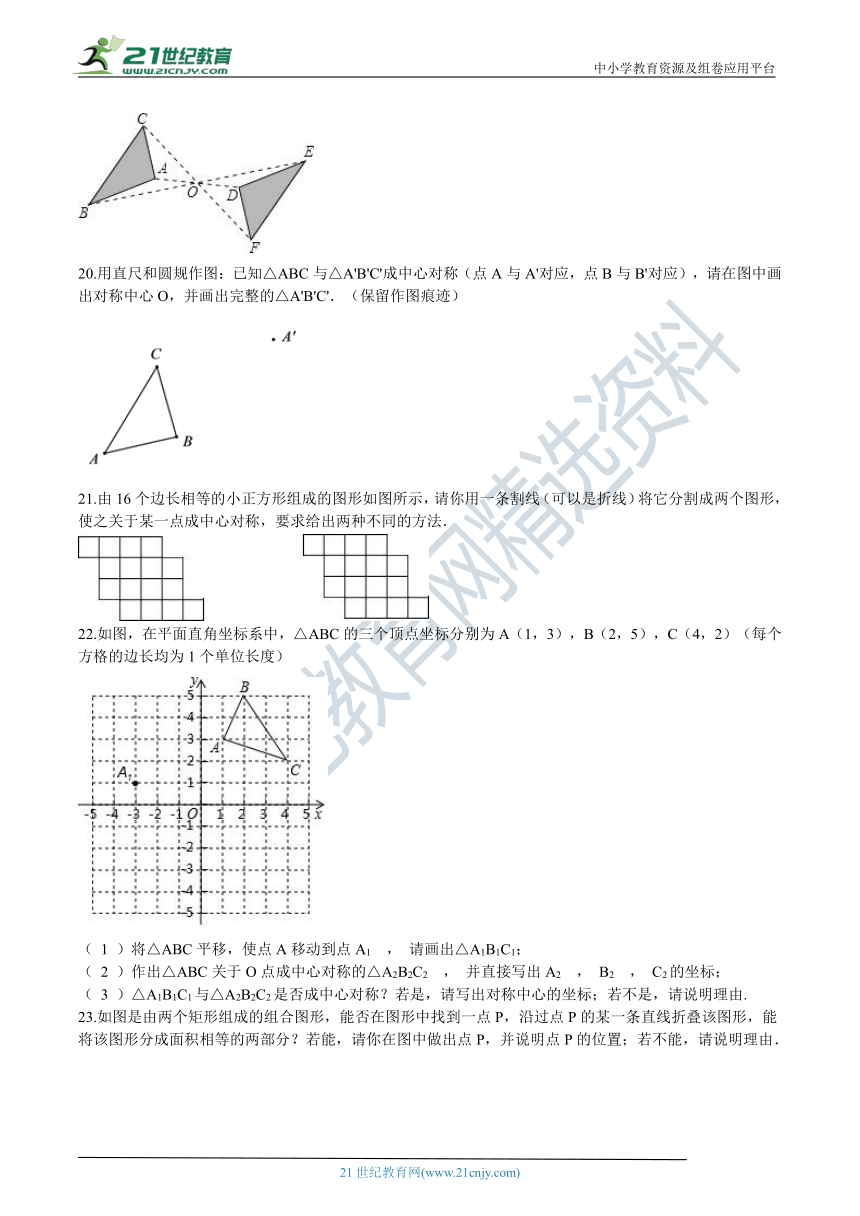
11.请写出一个是中心对称图形的几何图形的名称:________
12.六张完全相同的卡片上,分别画有等边三角形、正方形、矩形、平行四边形、圆、菱形,现从中随机抽取一张,卡片上画的恰好既是轴对称图形又是中心对称图形的概率为________.
13.如图,如果△ABC和△DEF关于点G成中心对称,那么△ABC绕点G旋转________°后能与△DEF重合.
14.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为________.
15.如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为________.
16.下列说法:
①成中心对称的两个图形全等;
②图形的旋转不改变图形的形状、大小;
③成中心对称的两个图形,对称点的连线被对称中心平分,
其中正确的个数为?________
.
17.在平面直角坐标系中,点P(1,1),N(2,0),△MNP和△M1N1P1的顶点都在格点上,△MNP与△M1N1P1是关于某一点中心对称,则对称中心的坐标为?________.
?
18.将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是________?cm2
.
三、解答题(本题共8题,共84分)
19.如图,△ABC与△DEF关于点O对称,请你写出两个三角形中的对称点,相等的线段,相等的角.
20.用直尺和圆规作图:已知△ABC与△A'B'C'成中心对称(点A与A'对应,点B与B'对应),请在图中画出对称中心O,并画出完整的△A'B'C'.(保留作图痕迹)
21.由16个边长相等的小正方形组成的图形如图所示,请你用一条割线(可以是折线)将它分割成两个图形,使之关于某一点成中心对称,要求给出两种不同的方法.
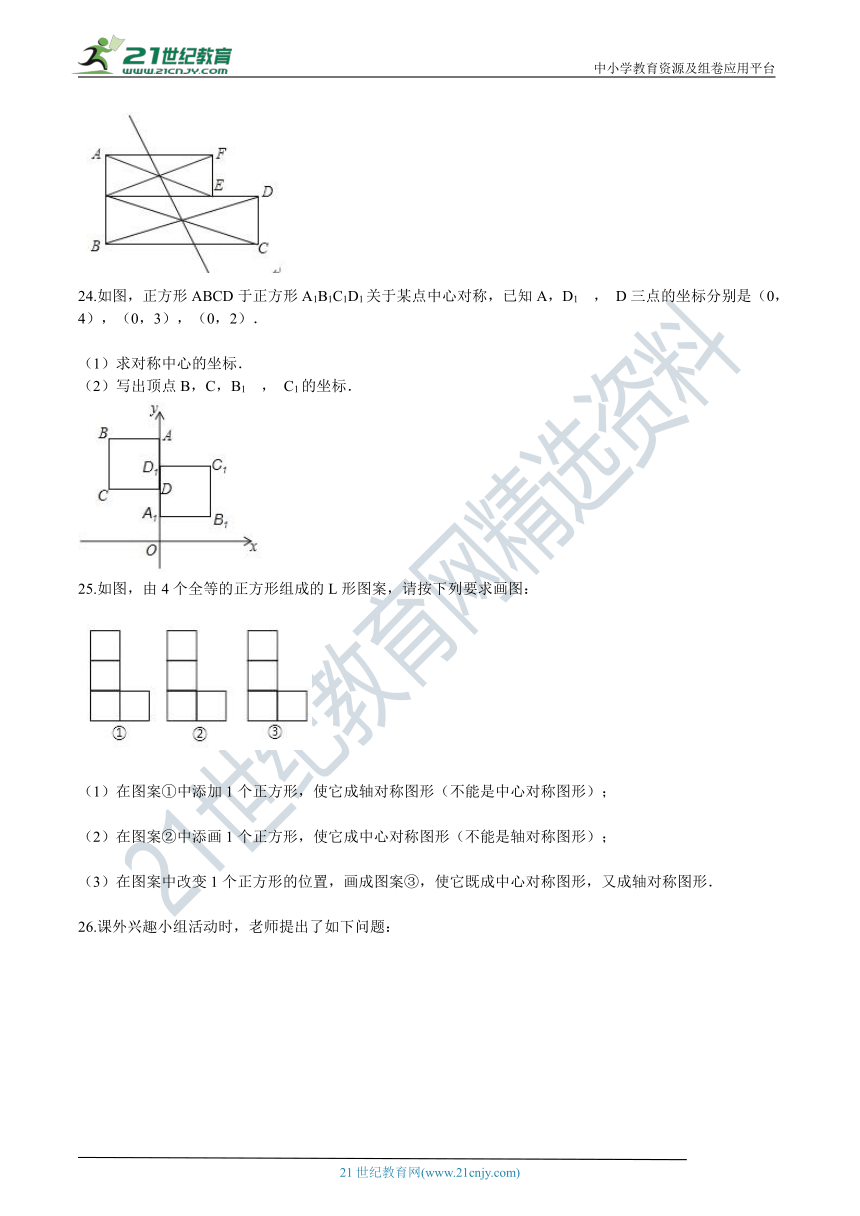
22.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,3),B(2,5),C(4,2)(每个方格的边长均为1个单位长度)
(
1
)将△ABC平移,使点A移动到点A1
,
请画出△A1B1C1;
(
2
)作出△ABC关于O点成中心对称的△A2B2C2
,
并直接写出A2
,
B2
,
C2的坐标;
(
3
)△A1B1C1与△A2B2C2是否成中心对称?若是,请写出对称中心的坐标;若不是,请说明理由.
23.如图是由两个矩形组成的组合图形,能否在图形中找到一点P,沿过点P的某一条直线折叠该图形,能将该图形分成面积相等的两部分?若能,请你在图中做出点P,并说明点P的位置;若不能,请说明理由.
?
24.如图,正方形ABCD于正方形A1B1C1D1关于某点中心对称,已知A,D1
,
D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标.
(2)写出顶点B,C,B1
,
C1的坐标.
25.如图,由4个全等的正方形组成的L形图案,请按下列要求画图:?
(1)在图案①中添加1个正方形,使它成轴对称图形(不能是中心对称图形);
(2)在图案②中添画1个正方形,使它成中心对称图形(不能是轴对称图形);
(3)在图案中改变1个正方形的位置,画成图案③,使它既成中心对称图形,又成轴对称图形.
26.课外兴趣小组活动时,老师提出了如下问题:
?
(1)如图1,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
[感悟]解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)解决问题:受到(1)的启发,请你证明下列命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
求证:BE+CF>EF,若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明.
答案解析部分
一、单选题
1.【答案】
D
解:A,是轴对称图形,但不是中心对称图形,故错误;
B,是轴对称图形,但不是中心对称图形,故错误;
C,是轴对称图形,也是中心对称图形,故错误;
D,不是轴对称图形,但是中心对称图形,故正确;
故答案为:D.
2.【答案】
B
解:正三角形是轴对称图形,不是中心对称图形,
等腰梯形是轴对称图形,不是中心对称图形,
矩形和圆既是轴对称图形,又是中心对称图形,
即既是轴对称图形,又是中心对称图形有2个,
故选B,
3.【答案】
C
解:A、全等的两个图形不一定成中心对称,A不符合题意;
B、成中心对称的两个图形是将其中一个图形绕对称中心旋转180°后与另一个图形重合即可,B不符合题意;
C、成中心对称的两个图形是将其中一个图形绕对称中心旋转180°后与另一个图形重合,因此这两个图形全等,C符合题意;
D、若旋转角度不是180°,则不一定成中心对称,D不符合题意;
故答案为:C
4.【答案】
D
解:∵此图形是中心对称图形,
∴对称中心是线段FC的中点.
故答案为:D.
5.【答案】
D
解:∵四边形ABCD与四边形A′B′C′D′关于点O成中心对称,
∴AB与A′B′的关系是相等并且平行或相等并且在同一直线上,
故选D.
6.【答案】
A
解:如图,连接HC和DE交于O1
,
故选A.
7.【答案】
D
解:A、AO=OE,错误;
B、BO=DO,错误;
C、点A关于点O的对称点是点E,错误;
D、点D
在BO的延长线上,正确;
故选D
8.【答案】
B
解:A、若将①涂黑,阴影部分不是中心对称图形,A不符合题意;
B、若将②涂黑,阴影部分是中心对称图形,B符合题意;
C、若将③涂黑,阴影部分不是中心对称图形,C不符合题意;
D、若将④涂黑,阴影部分不是中心对称图形,C不符合题意;
故答案为:B
9.【答案】
A
解:据旋转的性质,旋转前后图形的大小和形状没有改变,其必须是中心对称图形.分析可得只有第一张是中心对称图形;
故答案为:A.
.【答案】
D
解:根据中心对称图形的特点:?①对应点的连线必经过对称中心;②这两个图形的形状大小完全相同;③这两个图形的对应线段一定相等;④将一个图形绕对称中心旋转180°后必与另一个图形重合.
综上,四项都正确.
故答案为:D.?
二、填空题
11.【答案】
平行四边形
解:平行四边形是中心对称图形.
故答案可为:平行四边形.
12.【答案】
解:六个图形中,即是轴对称图形又是中心对称图形的有:正方形、矩形、圆、菱形,
∴P(即是轴对称又是中心对称图形)=
故答案为:.
13.【答案】
180
解:因为△ABC和△DEF关于点G成中心对称,所以△ABC绕点G旋转180°后能与△DEF重合.
故答案为:180.
14.【答案】
4
解:∵△ABC与△AB'C'关于点A对称,
∴AB=AB',
∵∠C=90°,∠B=30°,
∴AB=2AC=2,
∴AB‘=2AB=2×2=4.
故答案为:4.
15.【答案】
6
解:∵直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D,OB=3,OD=2,
∴AB=2,
∴阴影部分的面积之和为3×2=6.
故答案为:6.
16.【答案】3
解:①成中心对称的两个图形全等,正确,
②图形的旋转不改变图形的形状、大小,正确;
③成中心对称的两个图形,对称点的连线被对称中心平分,正确.
故答案为:3.
17.【答案】(2,1)
解:∵点P(1,1),N(2,0),
∴由图形可知M(3,0),M1(1,2),N1(2,2),P1(3,1),
∵关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分,
∴对称中心的坐标为(2,1),
故答案为:(2,1).
18.【答案】9
解:由中心对称的性质和正方形的性质得,一个阴影部分的面积等于正方形的面积的,
所以,四块阴影面积的总和正好等于一个正方形的面积,
∵五个正方形的边长都为3cm,
∴四块阴影面积的总和为9(cm2),
故答案为:9.
三、解答题
19.【答案】
解:对称点为:A和D、B和E、C和F;
相等的线段有AC=DF、AB=DE、BC=EF;
相等的角有:∠A=∠D,∠B=∠E,∠C=∠F
20.【答案】
解:连接
,作
的垂直平分线交
点O
如图,点
即为所求
如图,点
即为所求
如图,
即为所求
21.【答案】
解:如图所示:
22.【答案】
解:(1)如图,△A1B1C1为所作;
(
2
)如图,△A2B2C2为所作;点A2
,
B2
,
C2的坐标分别为(﹣1,﹣3),(﹣2,﹣5),(﹣4,﹣2);
(
3
)△A1B1C1与△A2B2C2关于点P中心对称,如图,
对称中心的坐标的坐标为(﹣2,﹣1).
23.【答案】
解:能,
如图:?
24.【答案】
解:(1)根据对称中心的性质,可得
对称中心的坐标是D1D的中点,
∵D1
,
D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,
∴B,C的坐标分别是(﹣2,4),(﹣2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1
,
C1的坐标分别是(2,1),(2,3),
综上,可得
顶点B,C,B1
,
C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).
25.【答案】
(1)如图(1),图(2),图(3)所示
?
(2)如图(4)所示
?
(3)如图(5),图(6)所示.
?
26.【答案】
(1)解:延长FD到G,使得DG=DF,连接BG、EG.
(或把△CFD绕点D逆时针旋转180°得到△BGD),
∴CF=BG=DF=DG,
∵DE⊥DF,
∴EF=EG.
在△BEG中,BE+BG>EG,即BE+CF>EF.
(2)解:若∠A=90°,则∠EBC+∠FCB=90°,
由(1)知∠FCD=∠DBG,EF=EG,
∴∠EBC+∠DBG=90°,即∠EBG=90°,
∴在Rt△EBG中,BE2+BG2=EG2
,
∴BE2+CF2=EF2
.
?
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
初中数学苏科版八年级下册
9.2
中心对称与中心对称图形
同步训练
一、单选题(本题共10题,每题3分,共30分)
1.下列图形中,是中心对称图形但不是轴对称图形的是(??
)
A.?????????????????????B.?????????????????????C.?????????????????????D.?
2.在正三角形、等腰梯形、矩形和圆这四种图形中,既是轴对称图形又是中心对称图形的有( )种.
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
3.下列说法正确的是(??
)
A.?全等的两个图形成中心对称????????????????????????????????B.?成中心对称的两个图形必须重合
C.?成中心对称的两个图形全等????????????????????????????????D.?旋转后能够重合的两个图形成中心对称
4.如图,已知图形是中心对称图形,则对称中心是(???
)
A.?点C????????????????????????????B.?点D????????????????????????????C.?线段BC的中点????????????????????????????D.?线段FC的中点
5.已知四边形ABCD与四边形A′B′C′D′关于点O成中心对称,则AB与A′B′的关系是(??
)
A.?相等???????????????B.?垂直???????????????C.?相等并且平行???????????????D.?相等并且平行或相等并且在同一直线上
6.如图,四边形ABD与四边形FGHE关于一个点成中心对称,则这个点是(??
)
A.?O1????????????????????????????????????????B.?O2????????????????????????????????????????C.?O3????????????????????????????????????????D.?O4
7.已知△ABC和△DEF关于点O对称,相应的对称点如图所示,则下列结论正确的是(??
)
A.?AO=BO????????????B.?BO=EO????????????C.?点A关于点O的对称点是点D????????????D.?点D
在BO的延长线上
8.如图,在方格纸中,选择标有序号①②③④的小正方形中的一个涂黑,
与图中阴影部分构成中心对称图形,则该小正方形的序号是(??
)
A.?①?????????????????????????????????????????B.?②?????????????????????????????????????????C.?③?????????????????????????????????????????D.?④
9.四张扑克牌如图①所示放在桌面上,小敏把其中一张旋转180°后得到图②,则她所旋转的牌从左数起是(??
)
A.?第一张????????????????????????????????B.?第二张????????????????????????????????C.?第三张????????????????????????????????D.?第四张
10.若两个图形成中心对称,则下列说法:①对应点的连线必经过对称中心;②这两个图形的形状大小完全相同;③这两个图形的对应线段一定相等;④将一个图形绕对称中心旋转180°后必与另一个图形重合.正确的有(???
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题(本题共8题,每题2分,共16分)
11.请写出一个是中心对称图形的几何图形的名称:________
12.六张完全相同的卡片上,分别画有等边三角形、正方形、矩形、平行四边形、圆、菱形,现从中随机抽取一张,卡片上画的恰好既是轴对称图形又是中心对称图形的概率为________.
13.如图,如果△ABC和△DEF关于点G成中心对称,那么△ABC绕点G旋转________°后能与△DEF重合.
14.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为________.
15.如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为________.
16.下列说法:
①成中心对称的两个图形全等;
②图形的旋转不改变图形的形状、大小;
③成中心对称的两个图形,对称点的连线被对称中心平分,
其中正确的个数为?________
.
17.在平面直角坐标系中,点P(1,1),N(2,0),△MNP和△M1N1P1的顶点都在格点上,△MNP与△M1N1P1是关于某一点中心对称,则对称中心的坐标为?________.
?
18.将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是________?cm2
.
三、解答题(本题共8题,共84分)
19.如图,△ABC与△DEF关于点O对称,请你写出两个三角形中的对称点,相等的线段,相等的角.
20.用直尺和圆规作图:已知△ABC与△A'B'C'成中心对称(点A与A'对应,点B与B'对应),请在图中画出对称中心O,并画出完整的△A'B'C'.(保留作图痕迹)
21.由16个边长相等的小正方形组成的图形如图所示,请你用一条割线(可以是折线)将它分割成两个图形,使之关于某一点成中心对称,要求给出两种不同的方法.
22.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,3),B(2,5),C(4,2)(每个方格的边长均为1个单位长度)
(
1
)将△ABC平移,使点A移动到点A1
,
请画出△A1B1C1;
(
2
)作出△ABC关于O点成中心对称的△A2B2C2
,
并直接写出A2
,
B2
,
C2的坐标;
(
3
)△A1B1C1与△A2B2C2是否成中心对称?若是,请写出对称中心的坐标;若不是,请说明理由.
23.如图是由两个矩形组成的组合图形,能否在图形中找到一点P,沿过点P的某一条直线折叠该图形,能将该图形分成面积相等的两部分?若能,请你在图中做出点P,并说明点P的位置;若不能,请说明理由.
?
24.如图,正方形ABCD于正方形A1B1C1D1关于某点中心对称,已知A,D1
,
D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标.
(2)写出顶点B,C,B1
,
C1的坐标.
25.如图,由4个全等的正方形组成的L形图案,请按下列要求画图:?
(1)在图案①中添加1个正方形,使它成轴对称图形(不能是中心对称图形);
(2)在图案②中添画1个正方形,使它成中心对称图形(不能是轴对称图形);
(3)在图案中改变1个正方形的位置,画成图案③,使它既成中心对称图形,又成轴对称图形.
26.课外兴趣小组活动时,老师提出了如下问题:
?
(1)如图1,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
[感悟]解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)解决问题:受到(1)的启发,请你证明下列命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
求证:BE+CF>EF,若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明.
答案解析部分
一、单选题
1.【答案】
D
解:A,是轴对称图形,但不是中心对称图形,故错误;
B,是轴对称图形,但不是中心对称图形,故错误;
C,是轴对称图形,也是中心对称图形,故错误;
D,不是轴对称图形,但是中心对称图形,故正确;
故答案为:D.
2.【答案】
B
解:正三角形是轴对称图形,不是中心对称图形,
等腰梯形是轴对称图形,不是中心对称图形,
矩形和圆既是轴对称图形,又是中心对称图形,
即既是轴对称图形,又是中心对称图形有2个,
故选B,
3.【答案】
C
解:A、全等的两个图形不一定成中心对称,A不符合题意;
B、成中心对称的两个图形是将其中一个图形绕对称中心旋转180°后与另一个图形重合即可,B不符合题意;
C、成中心对称的两个图形是将其中一个图形绕对称中心旋转180°后与另一个图形重合,因此这两个图形全等,C符合题意;
D、若旋转角度不是180°,则不一定成中心对称,D不符合题意;
故答案为:C
4.【答案】
D
解:∵此图形是中心对称图形,
∴对称中心是线段FC的中点.
故答案为:D.
5.【答案】
D
解:∵四边形ABCD与四边形A′B′C′D′关于点O成中心对称,
∴AB与A′B′的关系是相等并且平行或相等并且在同一直线上,
故选D.
6.【答案】
A
解:如图,连接HC和DE交于O1
,
故选A.
7.【答案】
D
解:A、AO=OE,错误;
B、BO=DO,错误;
C、点A关于点O的对称点是点E,错误;
D、点D
在BO的延长线上,正确;
故选D
8.【答案】
B
解:A、若将①涂黑,阴影部分不是中心对称图形,A不符合题意;
B、若将②涂黑,阴影部分是中心对称图形,B符合题意;
C、若将③涂黑,阴影部分不是中心对称图形,C不符合题意;
D、若将④涂黑,阴影部分不是中心对称图形,C不符合题意;
故答案为:B
9.【答案】
A
解:据旋转的性质,旋转前后图形的大小和形状没有改变,其必须是中心对称图形.分析可得只有第一张是中心对称图形;
故答案为:A.
.【答案】
D
解:根据中心对称图形的特点:?①对应点的连线必经过对称中心;②这两个图形的形状大小完全相同;③这两个图形的对应线段一定相等;④将一个图形绕对称中心旋转180°后必与另一个图形重合.
综上,四项都正确.
故答案为:D.?
二、填空题
11.【答案】
平行四边形
解:平行四边形是中心对称图形.
故答案可为:平行四边形.
12.【答案】
解:六个图形中,即是轴对称图形又是中心对称图形的有:正方形、矩形、圆、菱形,
∴P(即是轴对称又是中心对称图形)=
故答案为:.
13.【答案】
180
解:因为△ABC和△DEF关于点G成中心对称,所以△ABC绕点G旋转180°后能与△DEF重合.
故答案为:180.
14.【答案】
4
解:∵△ABC与△AB'C'关于点A对称,
∴AB=AB',
∵∠C=90°,∠B=30°,
∴AB=2AC=2,
∴AB‘=2AB=2×2=4.
故答案为:4.
15.【答案】
6
解:∵直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D,OB=3,OD=2,
∴AB=2,
∴阴影部分的面积之和为3×2=6.
故答案为:6.
16.【答案】3
解:①成中心对称的两个图形全等,正确,
②图形的旋转不改变图形的形状、大小,正确;
③成中心对称的两个图形,对称点的连线被对称中心平分,正确.
故答案为:3.
17.【答案】(2,1)
解:∵点P(1,1),N(2,0),
∴由图形可知M(3,0),M1(1,2),N1(2,2),P1(3,1),
∵关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分,
∴对称中心的坐标为(2,1),
故答案为:(2,1).
18.【答案】9
解:由中心对称的性质和正方形的性质得,一个阴影部分的面积等于正方形的面积的,
所以,四块阴影面积的总和正好等于一个正方形的面积,
∵五个正方形的边长都为3cm,
∴四块阴影面积的总和为9(cm2),
故答案为:9.
三、解答题
19.【答案】
解:对称点为:A和D、B和E、C和F;
相等的线段有AC=DF、AB=DE、BC=EF;
相等的角有:∠A=∠D,∠B=∠E,∠C=∠F
20.【答案】
解:连接
,作
的垂直平分线交
点O
如图,点
即为所求
如图,点
即为所求
如图,
即为所求
21.【答案】
解:如图所示:
22.【答案】
解:(1)如图,△A1B1C1为所作;
(
2
)如图,△A2B2C2为所作;点A2
,
B2
,
C2的坐标分别为(﹣1,﹣3),(﹣2,﹣5),(﹣4,﹣2);
(
3
)△A1B1C1与△A2B2C2关于点P中心对称,如图,
对称中心的坐标的坐标为(﹣2,﹣1).
23.【答案】
解:能,
如图:?
24.【答案】
解:(1)根据对称中心的性质,可得
对称中心的坐标是D1D的中点,
∵D1
,
D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,
∴B,C的坐标分别是(﹣2,4),(﹣2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1
,
C1的坐标分别是(2,1),(2,3),
综上,可得
顶点B,C,B1
,
C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).
25.【答案】
(1)如图(1),图(2),图(3)所示
?
(2)如图(4)所示
?
(3)如图(5),图(6)所示.
?
26.【答案】
(1)解:延长FD到G,使得DG=DF,连接BG、EG.
(或把△CFD绕点D逆时针旋转180°得到△BGD),
∴CF=BG=DF=DG,
∵DE⊥DF,
∴EF=EG.
在△BEG中,BE+BG>EG,即BE+CF>EF.
(2)解:若∠A=90°,则∠EBC+∠FCB=90°,
由(1)知∠FCD=∠DBG,EF=EG,
∴∠EBC+∠DBG=90°,即∠EBG=90°,
∴在Rt△EBG中,BE2+BG2=EG2
,
∴BE2+CF2=EF2
.
?
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
