9.4.1 矩形的性质同步训练（含解析）

中小学教育资源及组卷应用平台
初中数学苏科版八年级下册
9.4
矩形的性质
同步训练
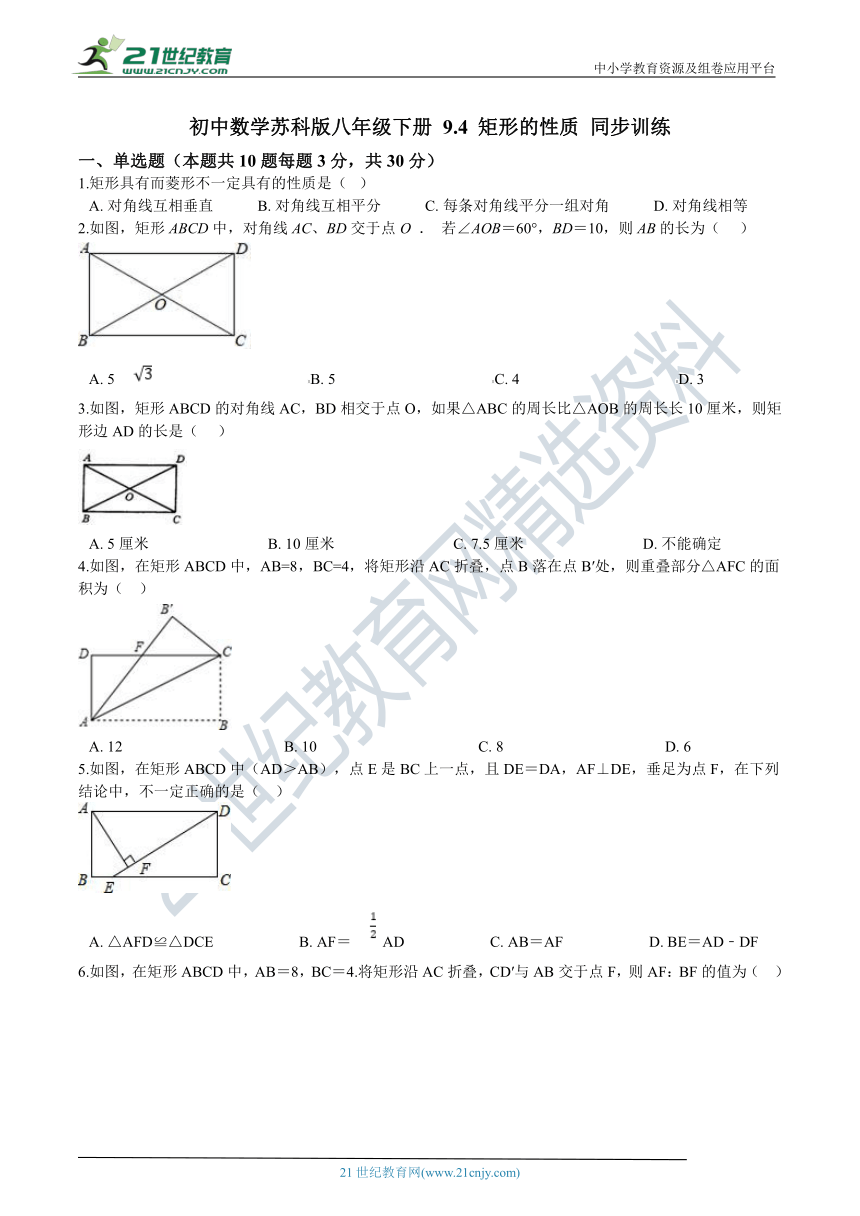
一、单选题（本题共10题每题3分，共30分）
1.矩形具有而菱形不一定具有的性质是（?
）
A.?对角线互相垂直???????????B.?对角线互相平分???????????C.?每条对角线平分一组对角???????????D.?对角线相等
2.如图，矩形ABCD中，对角线AC、BD交于点O
．
若∠AOB＝60°，BD＝10，则AB的长为（???
）
A.?5
?????????????????????????????????????????B.?5?????????????????????????????????????????C.?4?????????????????????????????????????????D.?3
3.如图，矩形ABCD的对角线AC，BD相交于点O，如果△ABC的周长比△AOB的周长长10厘米，则矩形边AD的长是（???
）
A.?5厘米???????????????????????????????B.?10厘米???????????????????????????????C.?7.5厘米???????????????????????????????D.?不能确定
4.如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点B落在点B′处，则重叠部分△AFC的面积为（??
）
A.?12??????????????????????????????????????????B.?10??????????????????????????????????????????C.?8??????????????????????????????????????????D.?6
5.如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE＝DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（??
）
A.?△AFD≌△DCE??????????????????????B.?AF＝
AD??????????????????????C.?AB＝AF??????????????????????D.?BE＝AD﹣DF
6.如图，在矩形ABCD中，AB＝8，BC＝4.将矩形沿AC折叠，CD′与AB交于点F，则AF：BF的值为（??
）
A.?2?????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
7.如图，四边形
OABC
是矩形，A（2，1），B（0，5），点
C
在第二象限，则点
C
的坐标是（????
）
A.?（1，3）??????????????????????B.?（﹣1，2）??????????????????????C.?（﹣2，﹣3）??????????????????????D.?（﹣2，4）
8.如图，把矩形ABCD折叠，使点C落在点A处，点D落在点G处，若∠FED=120°，且DE=2，则边BC的长为（
??）
A.?????????????????????????????????????B.?????????????????????????????????????C.?8　????????????????????????????????????D.?6
9.如图，
，矩形
在
的内部，顶点
，
分别在射线
，
上，
，
，则点
到点
的最大距离是（???
）　
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
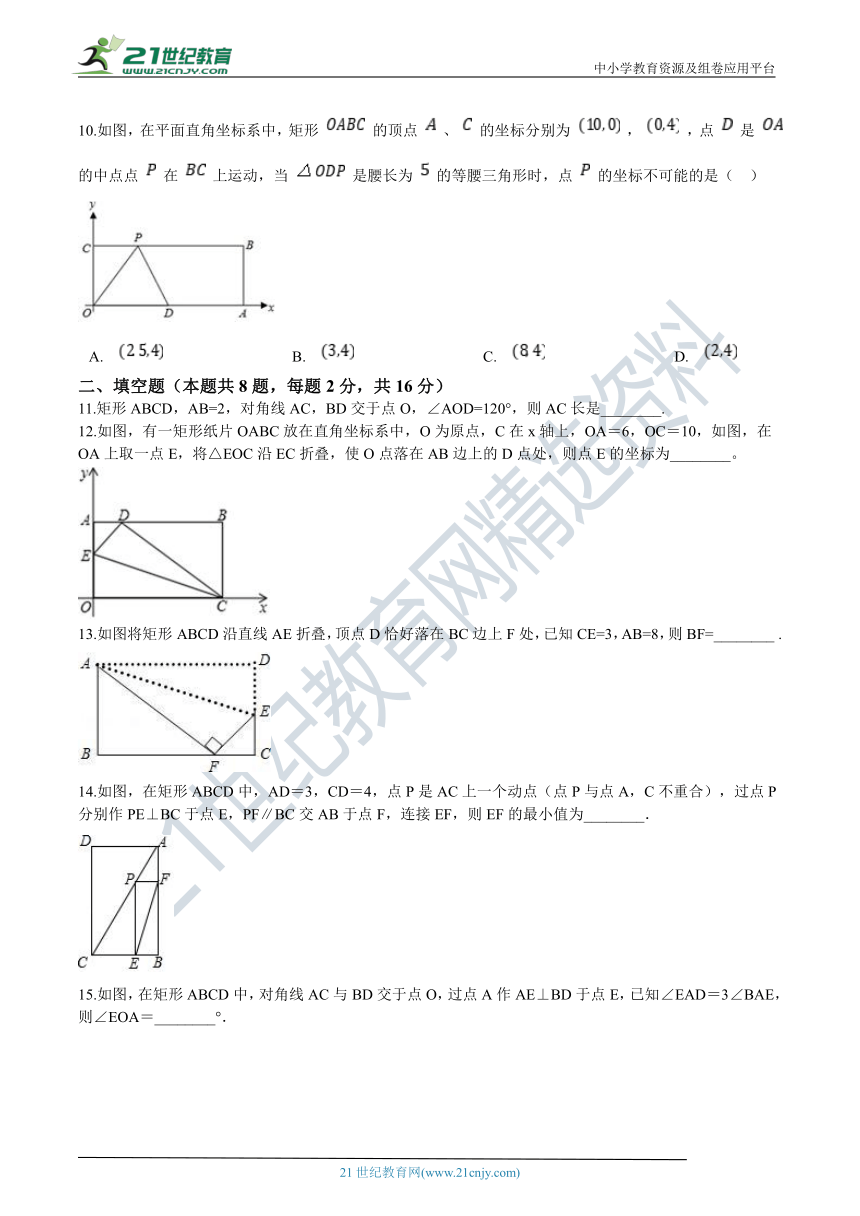
10.如图，在平面直角坐标系中，矩形
的顶点
、
的坐标分别为
，
，点
是
的中点点
在
上运动，当
是腰长为
的等腰三角形时，点
的坐标不可能的是（??
）
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
二、填空题（本题共8题，每题2分，共16分）
11.矩形ABCD，AB=2，对角线AC，BD交于点O，∠AOD=120°，则AC长是________.
12.如图，有一矩形纸片OABC放在直角坐标系中，O为原点，C在x轴上，OA＝6，OC＝10，如图，在OA上取一点E，将△EOC沿EC折叠，使O点落在AB边上的D点处，则点E的坐标为________。
13.如图将矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上F处，已知CE=3，AB=8，则BF=________
.
14.如图，在矩形ABCD中，AD＝3，CD＝4，点P是AC上一个动点（点P与点A，C不重合），过点P分别作PE⊥BC于点E，PF∥BC交AB于点F，连接EF，则EF的最小值为________．
15.如图，在矩形ABCD中，对角线AC与BD交于点O，过点A作AE⊥BD于点E，已知∠EAD＝3∠BAE，则∠EOA＝________°．
16.如图，P是矩形ABCD的边AD上一个动点，矩形的两条边AB、BC的长分别为6和8，那么点P到矩形的两条对角线AC和BD的距离之和是________.
17.如图，矩形纸片ABCD，AB＝8，BC＝6，点P在BC边上，将△CDP沿DP折叠，点C落在E处，PE，DE分别交AB于点O，F，且OP＝OF，则AF长为________.
18.如图，在直角坐标系中，矩形
ABCO
的边
OA
在
x
轴上，边
OC
在
y
轴上，点
B
的坐标为（3，4），直线
CD
分别交
OB、AB
于点
D、E，若
BD＝BE，则点
D
的坐标为________.
三、解答题（本题共10题，共84分）
19.如图，在长方形ABCD中，已知AB=8cm，BC=10cm，将AD沿AF折叠，使点D落在BC上的点E处.求BE及CF的长.
20.如图所示，将长方形
沿直线
折叠，使点
落在点
处，
交
于
，
，
，求
的长.
21.如图，矩形ABCD中，AC、BD相交于O，AE平分∠BAD交BC于E，若∠CAE=15°，求∠BOE的度数．
22.如图，长方形ABCD中，AB＝6，BC＝8，点E是BC边上一点，连接AE，把△ABE沿AE折叠，使点B落在点B'处．当△CEB'为直角三角形时，求BE的长？
23.如图，将长方形ABCD沿EF折叠，使顶点C恰好落在AB边的中点
上．若
，
，求BF的长．
24.如图，在矩形ABCD中，AB＝8，BC＝4，将矩形沿对角线AC折叠，点D落在D′处．
（1）求证：AF＝CF
（2）求重叠部分△AFC的面积．
25.在矩形纸片ABCD中，AB=6，BC=8，
（1）将矩形纸片沿BD折叠，点A落在点E处（如图①），设DE与BC相交于点F，试说明△DBF是等腰三角形，并求出其周长．
（2）将矩形纸片折叠，使点B与点D重合（如图②），求折痕GH的长．
26.一张矩形纸片，剪下一个正方形，剩下一个矩形，称为第一次操作；在剩下的矩形纸片中再剪下一个正方形，剩下一个矩形，称为第二次操作；；若在第n次操作后，剩下的矩形为正方形，则称原矩形为n阶奇异矩形．如图1，矩形ABCD中，若AB=2，BC=6，则称矩形ABCD为2阶奇异矩形．
（1）判断与操作：如图2，矩形ABCD长为5，宽为2，它是奇异矩形吗？如果是，请写出它是几阶奇异矩形，并在图中画出裁剪线；如果不是，请说明理由．
（2）探究与计算：已知矩形ABCD的一边长为20，另一边长为a（a＜20），且它是3阶奇异矩形，请画出矩形ABCD及裁剪线的示意图，并在图的下方写出a的值．
（3）归纳与拓展：已知矩形ABCD两邻边的长分别为b，c（b＜c），且它是4阶奇异矩形，则b:c=___________________________________________（写出所有值）．
27.如图1，已知长方形ABCD，AB＝4，BC＝6，E为CD边的中点，P为长方形ABCD边上的动点，点P从A出发，以每秒2个单位的速度沿着A→B→C运动，设P运动的时间为t秒.
（1）当△APE是以EP为腰的等腰三角形时，求t的值；
（2）当P在线段BC上运动时，是否存在点P使得△APE的周长最小？若存在，求出此时t的值；若不存在，请说明理由.
28.在长方形纸片ABCD中，点E是边CD上的一点，将△AED沿AE所在的直线折叠，使点D落在点F处.
（1）如图1，若点F落在对角线AC上，且∠BAC＝54°，则∠DAE的度数为________°.
（2）如图2，若点F落在边BC上，且AB＝6，AD＝10，求CE的长.
（3）如图3，若点E是CD的中点，AF的沿长线交BC于点G，且AB＝6，AD＝10，求CG的长.
答案解析部分
一、单选题
1.【答案】
D
解：∵矩形具有的性质：对角线相等，对角线互相平分,四个角都是直角；
菱形具有的性质：四边相等，对角线互相平分，对角线互相垂直，每一条对角线平分一组对角，对角相等；
∴A、对角线互相垂直是菱形具有，矩形不一定具有的性质，不符合题意；
B、对角线互相平分是矩形和菱形都具有的性质，不符合题意；
C、每条对角线平分一组对角是菱形具有的，但矩形不一定具有，不符合题意；
D、对角相等是矩形和菱形都具有的性质，符合题意.
故答案为：D.
2.【答案】
B
解：∵四边形ABCD是矩形，
∴AC＝BD
，
AO＝BO＝CO＝DO
，
∵∠AOB＝60°，
∴△AOB是等边三角形，
∴AB＝
BD＝5．
故答案为：B
．
3.【答案】
B
解：∵四边形ABCD是矩形，
∴AO=CO=DO=BO，AD=BC，
∵△ABC的周长=AB+AC+BC=AB+AO+OC+BC，△AOB的周长=AB+AO+BO，
又∵△ABC的周长比△AOB的周长长10厘米，
∴AB+AC+BC=AB+AO+OC+BC-（AB+AO+BO）=BC=10厘米，
∵AD=BC，
∴AD的长是10厘米。
故答案为：B。
4.【答案】
B
解：由翻折变换的性质可知，
，
，
设
，则
，
在
中，
，即
，
解得：
，
，
.
故答案为：
.
5.【答案】
B
解：A.由矩形ABCD，AF⊥DE可得∠C=∠AFD=90°，AD∥BC，∴∠ADF=∠DEC.
又∵DE=AD，∴△AFD≌△DCE（AAS），故A正确；
B.∵∠ADF不一定等于30°，∴直角三角形ADF中，AF不一定等于AD的一半，故B错误；
C.由△AFD≌△DCE，可得AF=CD，由矩形ABCD，可得AB=CD，∴AB=AF，故C正确；
D.由△AFD≌△DCE，可得CE=DF，由矩形ABCD，可得BC=AD，又∵BE=BC﹣EC，∴BE=AD﹣DF，故D正确；
故答案为：B.
6.【答案】
B
解：设BF＝x，
∵将矩形沿AC折叠，
∴∠DCA＝∠ACF，
∵四边形ABCD是矩形，
∴CD∥AB，
∴∠DCA＝∠CAB＝∠ACF，
∴FA＝FC＝8﹣x，
在Rt△BCF中，∵CF2＝BC2+BF2
，
∴（8﹣x）2＝x2+42
，
∴x＝3，
∴BF＝3，
∴AF＝5，
∴AF：BF的值为
，
故答案为：B.
7.【答案】
D
解：过C作CE⊥y轴与E，过A作AF⊥y轴于F．
∴∠CEO=∠AFB=90°
∵四边形ABCO为矩形
∴AB=OC，AB
OC
∴∠ABF=∠COE
∴△OCE≌△BAF（AAS）
同理可得
∴△BCE≌△OAF（AAS）
∴CE=AF，OE=BF，BE=OF
∵A（2，1），B（0，5）
∴AF=CE=2，BE=OF=1，OB=5
∴OE=4,
∴点C的坐标为（-2，4）
故答案为：D．
8.【答案】
D
根据翻折变换的特点可知：DE=GE=2，
∵∠FED=120°，
∴∠GEF=120°，∠AEF=60°
∴∠GEA=60°
∴∠GAE=30°，
则AE=2GE=4，
∴BC=AD=AE+DE=6
故选D.
9.【答案】
B
解：取
中点
，连接
、
、
，
，
.
在
中，利用勾股定理可得
.
在
中，根据三角形三边关系可知
，
当
、
、
三点共线时，
最大为
.
故答案为：
.
10.【答案】
A
解：由题意，当△ODP是腰长为5的等腰三角形时，有三种情况：①.如答图①所示，PD＝OD＝5，点P在点D的左侧.
过点P作PE⊥x轴于点E，则PE＝4.
在Rt△PDE中，由勾股定理得：DE＝3，
∴OE＝OD?DE＝5?3＝2，
∴此时点P坐标为（2，4）；②.如答图②所示，OP＝OD＝5.
过点P作PE⊥x轴于点E，则PE＝4.
在Rt△POE中，由勾股定理得：OE＝3，
∴此时点P坐标为（3，4）；③.如答图③所示，PD＝OD＝5，点P在点D的右侧.
过点P作PE⊥x轴于点E，则PE＝4.
在Rt△PDE中，由勾股定理得：DE＝3，
∴OE＝OD＋DE＝5＋3＝8，
∴此时点P坐标为（8，4）.
∴点P的坐标不可能是
，
故答案为：A.
二、填空题
11.【答案】
4
解：∵四边形ABCD是矩形，
∴AC=BD，OA=OC，OB=OD，
∴OA=OB，
∵∠AOD=120°，
∴∠AOB=60°，
∴△AOB是等边三角形，
∴OA=OB=AB=2，
∴AC=2OA=4，
12.【答案】
解：由矩形的性质得：
由翻转变换的性质得：
在
中，
则
设
，则
在
中，
，即
解得
故点E的坐标为
.
故答案为：
.
13.【答案】
6
解：由折叠的性质知：AD=AF，DE=EF=8﹣3=5；
在Rt△CEF中，EF=DE=5，CE=3，由勾股定理可得：CF=4，
若设AD=AF=x，则BC=x，BF=x﹣4；
在Rt△ABF中，由勾股定理可得：
82+（x﹣4）2=x2
，
解得x=10，
故BF=x﹣4=6.
故答案为：6.
14.【答案】
解：证明：如图，连接BP．
∵∠B＝∠D＝90°，AD＝3，CD＝4，
∴AC＝5，
∵PE⊥BC于点E，PF∥BC，∠B＝90°，
∴四边形PEBF是矩形；
∴EF＝BP，
由垂线段最短可得BP⊥AC时，线段EF的值最小，
此时，S△ABC＝
BC?AB＝
AC?CP，
即
×4×3＝
×5?CP，
解得CP＝
．
故答案为：
．
15.【答案】
解：∵四边形ABCD是矩形，
∴
，OA=OB，
∵∠EAD＝3∠BAE，
∴
，
∴
，
∵AE⊥BD，
∴
，
∴
，
．
故答案是
．
16.【答案】
4.8
解：连接OP，
∵矩形的两条边AB、BC的长分别为6和8，
∴S矩形ABCD＝AB?BC＝48，OA＝OC，OB＝OD，AC＝BD＝
，
∴OA＝OD＝5，
∴S△ACD＝
S矩形ABCD＝24，
∴S△AOD＝
S△ACD＝12，
∵S△AOD＝S△AOP＋S△DOP＝
OA?PE＋
OD?PF＝
×5×PE＋
×5×PF＝
（PE＋PF）＝12，
解得：PE＋PF＝4.8.
故答案为：4.8.
17.【答案】
解：∵
将△CDP沿DP折叠，点C落在E处，
∴DC=DE=8，CP=EP，
在△OEF和△OBP中，
，
∴△OEF≌△OBP（AAS），
∴OE=OB，EF=BP，
设EF=BP=x，
DF=DE-EF=8-x，
∵BF=OB+OF=OE+OP=PE=PC，PC=BC-BP=6-x，
∴AF=AB-BF=2+x，
在Rt△DAF中，AF2+AD2=DF2
，
∴（2+x）2+62=（8-x）2
，
∴x=,
∴AF=2+x=.
故答案为：.
18.【答案】
解：∵四边形ABCO是矩形，点B的坐标为（3,4），
∴BC=OA=3，OC=AB=4，OC∥AB,
∴C（0,4），
∵BD=BE，
∴∠BDE=∠BED，
∵OC∥AB，
∴∠OCE=∠BED，又∠CDO=∠BDE，
∴∠OCD=∠ODC，
∴OD=OC=4，
在RtΔOAB中，OA=3，AB=4，由勾股定理得
OB=
=5，
∴BD=BE=1，
∴E（3,3），
∴直线CE的解析式：
，
直线OB的解析式：
，
联立方程组
，解得：
，
∴
，
故答案为：
.
三、解答题
19.【答案】
解：∵四边形ABCD是矩形，
∴AD=BC=10cm，CD=AB=8cm，
根据题意得：Rt△ADF≌Rt△AEF，
∴∠AEF=90°，AE=10cm，EF=DF，
设CF=xcm，则DF=EF=CD-CF=（8-x）cm，
在Rt△ABE中由勾股定理得：AB2+BE2=AE2
，
即82+BE2=102
，
∴BE=6cm，
∴CE=BC-BE=10-6=4（cm），
在Rt△ECF中，由勾股定理可得：EF2=CE2+CF2
，
即（8-x）2=x2+42
，
∴64-16x+x2=x2+16，
∴x=3（cm），
即CF=3cm.
20.【答案】
解：∵四边形
是矩形，
∴
∥
，
∴
，
由折叠的性质得：
，
∴
，
∴
，
设
，则
．
在
中，由勾股定理得：
，
∴
解得：
，
∴
．
故
的长为
．
21.【答案】
解：∵AE平分∠BAD交BC于E，∴∠AEB=45°，AB=BE，∵∠CAE=15°，∴∠ACB=∠AEB﹣∠CAE=45°﹣15°=30°，∴∠BAO=60°，又∵OA=OB，∴△BOA是等边三角形，∴OA=OB=AB，即OB=AB=BE，∴△BOE是等腰三角形，且∠OBE=∠OCB=30°，∠BOE=
=75°．
22.【答案】
解：①、当B′EC为直角时，则∠BEB′也是直角，根据折叠的性质可得∠AEB=45°，则△ABE为等腰直角三角形，则BE=AE=6；②、当∠EB′C为直角时，根据折叠可得∠AB′E=∠ABE=90°，则点A、点B′、点C三点共线，则AB′=AB=6，AC=10，则B′C=10－6=4，设BE=x，则CE=8－x，B′E=x，根据Rt△B′EC的勾股定理可得：
，解得x=3，即BE=3.
23.【答案】
解：∵将长方形ABCD沿EF折叠，使顶点C恰好落在AB边的中点C′上
∴BC'=
AB=3，CF=C'F
在Rt△BC'F中，C'F2=BF2+C'B2
，
∴CF2=（9-CF）2+9
∴CF=5
∴BF=4．
24.【答案】
（1）证明：依题意可知，矩形沿对角线AC对折后有：
∠D′＝∠B＝90°，∠AFD′＝∠CFB，BC＝AD′
∴△AD′F≌△CBF（AAS）
∴CF＝AF
（2）解：设AF＝CF＝x
∴BF＝8﹣x
在Rt△BCF中有BC2+BF2＝FC2
即42+（8﹣x）2＝x2
解得x＝5．
∴S△AFC＝
AF?BC＝
×5×4＝10．
25.【答案】
（1）解：由折叠得，∠ADB=∠EDB，
在矩形ABCD中：∠C=90°，CD=AB=6,AD∥BC，
∴∠ADB=∠DBC，
∴∠FBD=∠FDB，
∴BF=DF，
设BF=x，则CF=8?x，
在Rt△CDF中，
即
解得
∴
在Rt△BCD中：∠C=90°，CD=6，BC=8，
∴
∴△DBF的周长是：BF+DF+DB=
（2）解：由折叠得，DH=BH，设BH=DH=x，则CH=8?x，
在Rt△CDH中，
即
解得
连接BD、BG，
由翻折的性质可得，BG=DG，∠BHG=∠DHG，
∵矩形ABCD的边AD∥BC，
∴∠BHG=∠DGH，
∴∠DHG=∠DGH，
∴DH=DG，
∴BH=DH=DG=BG，
∴四边形BHDG是菱形，
在Rt△BCD中：∠C=90°，CD=6，BC=8，
∴
∴S菱形BHDG=
BD?GH=BH?CD，
即
×10?GH=
×6，
解得GH=
．
26.【答案】
（1）矩形ABCD是3阶奇异矩形，裁剪线的示意图如下：
（2）裁剪线的示意图如下：
（3）b：c的值为
，
，
，
，
，
，
，
．
规律如下：第4次操作前短边与长边之比为：；
第3次操作前短边与长边之比为：
，
；
第2次操作前短边与长边之比为：
，
，
，
；
第1次操作前短边与长边之比为：
，
，
，
，
，
，
，
．
27.【答案】
（1）当AE=EP时，
∵E点为DC的中点，DC=4，AD=6，
∴DE=EC=2，
∴
，
∴EP=
,此时P点与B点重合，运动路程为AB=4，
∴t=4÷2=2（秒），
当AP=PE时，P点在线段BC上，
∵P点的运动路程为：AB+BP=2t，
∴BP=2t-4，PC=10-2t，
∵
，
∴(2t-4)2+42=22+(10-2t)2
解得：t=3
综上所述：当t=2或t=3时，△APE是以EP为腰的等腰三角形，
（2）存在，
如图所示，作点E关于直线BC的对称点F，连接AF与BC的交点为P，连接AE、PE
此时△APE的周长最小，
∴CF=CE=ED=2，
∴DF=6，
∵AD=6，
∴△ADF是等腰直角三角形，
∴∠F=45°，
∵四边形ABCD是长方形，
∴AB∥DF，
∴∠BAP=∠F=45°，
∴△ABP是等腰直角三角形，
故AB=BP=4，
∴运动时间为：（4+4）÷2=4（秒）
28.【答案】
（1）18
（2）解：∵四边形ABCD是矩形，
∴∠B＝∠C＝90°，BC＝AD＝10，CD＝AB＝6，
由折叠的性质得：AF＝AD＝10，EF＝ED，
∴BF＝
＝
＝8，
∴CF＝BC﹣BF＝10﹣8＝2，
设CE＝x，则EF＝ED＝6﹣x，
在Rt△CEF中，由勾股定理得：22+x2＝（6﹣x）2
，
解得：x＝
，
即CE的长为
；
（3）解：连接EG，如图3所示：
∵点E是CD的中点，
∴DE＝CE，
由折叠的性质得：AF＝AD＝10，∠AFE＝∠D＝90°，FE＝DE，
∴∠EFG＝90°＝∠C，
在Rt△CEG和△FEG中，
，
∴Rt△CEG≌△FEG（HL），
∴CG＝FG，
设CG＝FG＝y，
则AG＝AF+FG＝10+y，BG＝BC﹣CG＝10﹣y，
在Rt△ABG中，由勾股定理得：62+（10﹣y）2＝（10+y）2
，
解得：y＝
，
即CG的长为
.
解：（1）∵四边形ABCD是矩形，
∴∠BAD＝90°，
∵∠BAC＝54°，
∴∠DAC＝90°﹣54°＝36°，
由折叠的性质得：∠DAE＝∠FAE，
∴∠DAE＝
∠DAC＝18°；
故答案为：18；
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)