9.4.3 菱形的判定及性质同步训练(含解析)
文档属性
| 名称 | 9.4.3 菱形的判定及性质同步训练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 10:01:42 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
初中数学苏科版八年级下册
9.4
菱形的判定及性质
同步训练
一、单选题(本题共10题,每题3分,共30分)
1.下列命题中,真命题是( ).
A.?对角线相等且互相垂直的四边形是菱形???????????????B.?有一条对角线平分对角的四边形是菱形
C.?菱形是对角线互相垂直平分的四边形??????????????????D.?菱形的对角线相等
2.菱形的两条对角线的长分别为6和8,则菱形的高为(
)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
3.如图,在平行四边形ABCD中,AC平分∠DAB
,
AB=2,则平行四边形ABCD的周长为( ).?
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?12
4.如图,在
ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF.则四边形AECF是(???
)
A.?梯形????????????????????????????????????B.?矩形????????????????????????????????????C.?菱形????????????????????????????????????D.?正方形
5.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,AF平分∠CAB交CD于E,交CB于F,且EG∥AB交CB于G,则CF与GB的大小关系是(
??)
A.?CF>GB?????????????????????????????B.?GB=CF?????????????????????????????C.?CF<GB?????????????????????????????D.?无法确定
6.如图,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为( )
A.?1?????????????????????????????????????????B.??????????????????????????????????????????C.?2?????????????????????????????????????????D.?
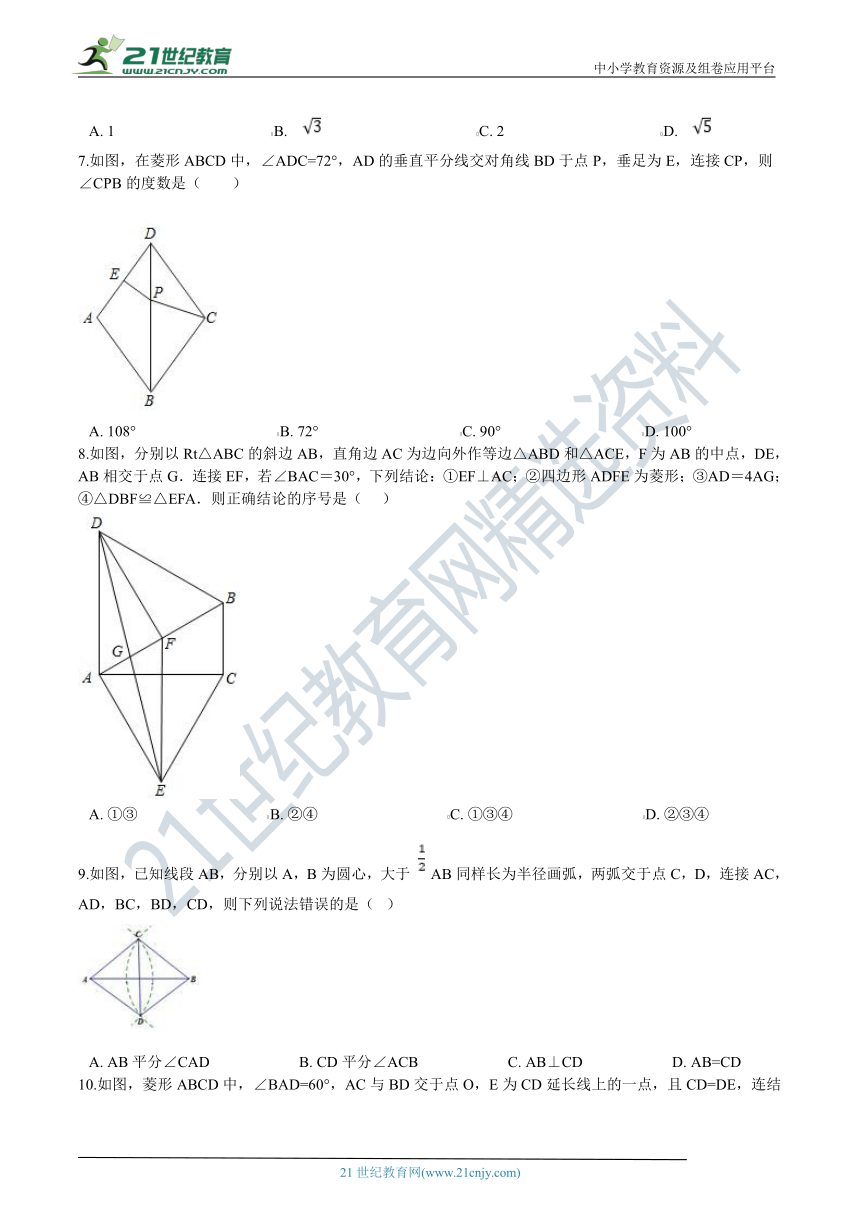
7.如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB的度数是( )
A.?108°?????????????????????????????????????B.?72°?????????????????????????????????????C.?90°?????????????????????????????????????D.?100°
8.如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G.连接EF,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.则正确结论的序号是(???
)
A.?①③??????????????????????????????????B.?②④??????????????????????????????????C.?①③④??????????????????????????????????D.?②③④
9.如图,已知线段AB,分别以A,B为圆心,大于
AB同样长为半径画弧,两弧交于点C,D,连接AC,AD,BC,BD,CD,则下列说法错误的是(?
)
A.?AB平分∠CAD???????????????????????B.?CD平分∠ACB???????????????????????C.?AB⊥CD???????????????????????D.?AB=CD
10.如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE,分别交AC,AD于点F、G,连结OG,则下列结论:
①OG=
AB;②图中与△EGD全等的三角形共有5个;③由点A、B、D、E构成的四边形是菱形;④S四边形ODGF=S△ABF
,
其中正确的结论是(??
)
A.?①③?????????????????????????????????B.?①③④?????????????????????????????????C.?①②③?????????????????????????????????D.?②③④
二、填空题(本题共6题,每题2分,共12分)
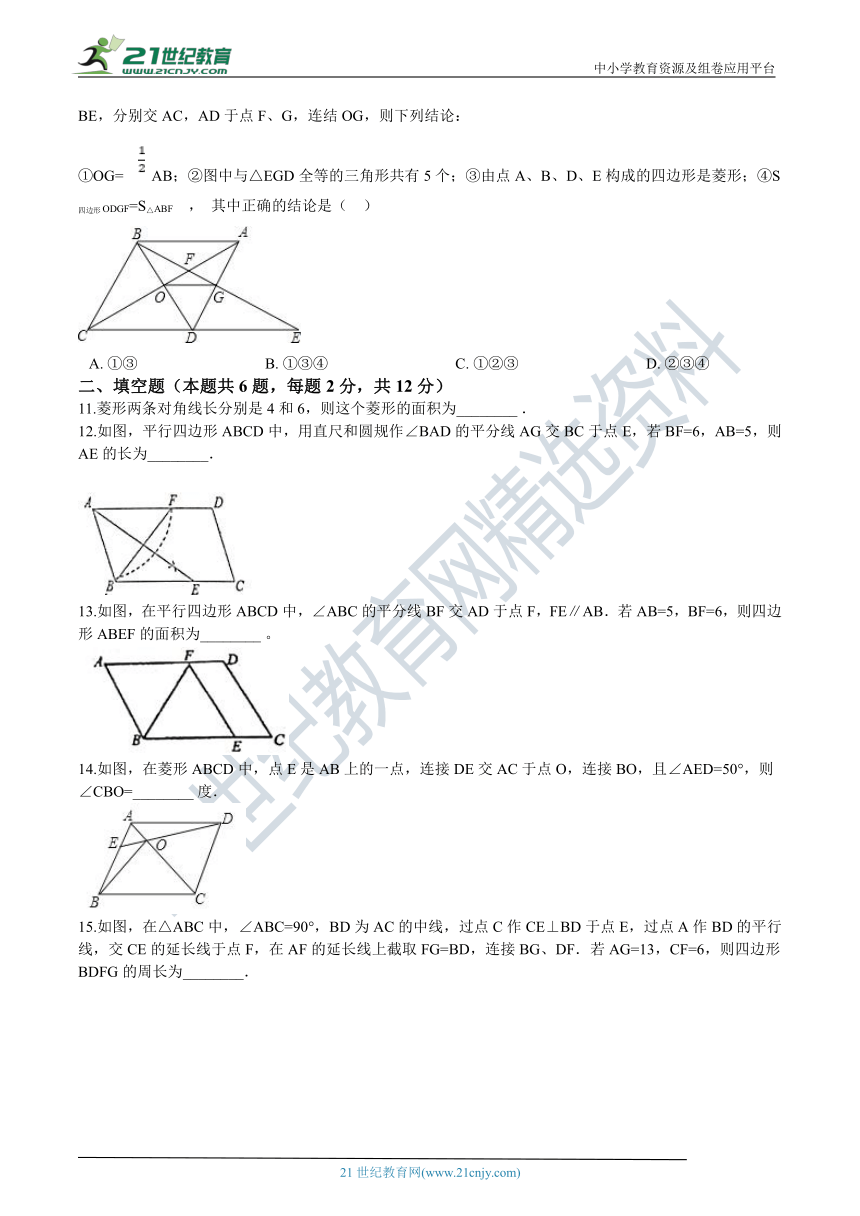
11.菱形两条对角线长分别是4和6,则这个菱形的面积为________?.
12.如图,平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为________.
13.如图,在平行四边形ABCD中,∠ABC的平分线BF交AD于点F,FE∥AB.若AB=5,BF=6,则四边形ABEF的面积为________?。
14.如图,在菱形ABCD中,点E是AB上的一点,连接DE交AC于点O,连接BO,且∠AED=50°,则∠CBO=________?度.
15.如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则四边形BDFG的周长为________.
16.在数学课上,老师提出如下问题:
尺规作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A.
求作:l的平行线,使它经过点A.
小云的作法如下:(1)在直线l上任取一点B;(2)以B为圆心,BA长为半径作弧,交直线l于点C;(3)分别以A、C为圆心,BA长为半径作弧,两弧相交于点D;(4)作直线AD.直线AD即为所求.
小云作图的依据是________.
三、解答题(本题共9题,共88分)
17.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE
,
过点C作CF∥BE交DE的延长线于F
.
求证:四边形BCFE是菱形.
18.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F
(1)求证:△AEF≌△DEB;
(2)证明:四边形ADCF是菱形;
(3)若AB=4,AC=5,求菱形ADCF的面积.
?
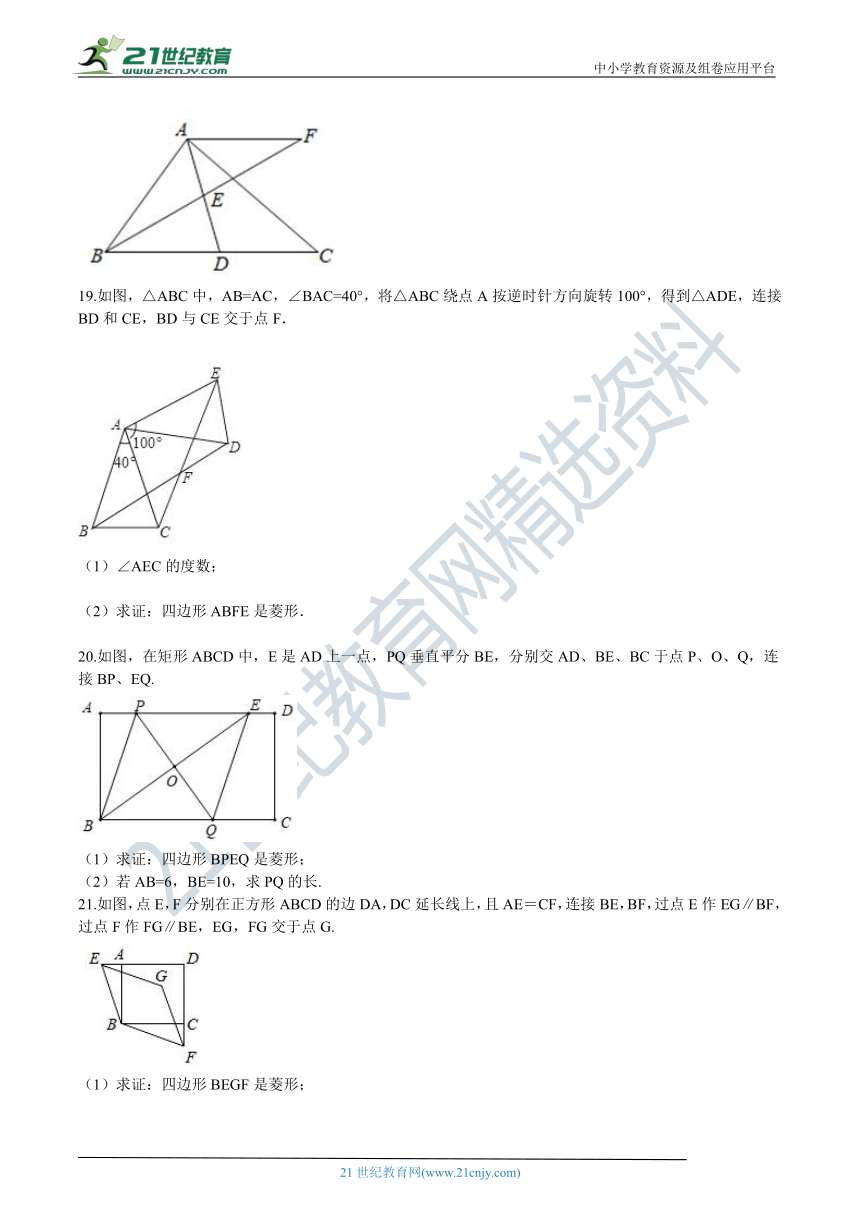
19.如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD和CE,BD与CE交于点F.
(1)∠AEC的度数;
(2)求证:四边形ABFE是菱形.
20.如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,BE=10,求PQ的长.
21.如图,点E,F分别在正方形ABCD的边DA,DC延长线上,且AE=CF,连接BE,BF,过点E作EG∥BF,过点F作FG∥BE,EG,FG交于点G.
(1)求证:四边形BEGF是菱形;
(2)若AD=3AE=6,求四边形BEGF的周长.
22.在Rt△ABC中,∠BAC=
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD
的面积.
23.如图,在矩形ABCD中,E是AD边上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、QE
(1)求证:四边形BPEQ是菱形:
(2)若AB=6,F是AB中点,OF=4,求菱形BPEQ的面积.
24.如图,在平面直角坐标系中,直线
∶
分别与
轴、
轴交于点B、C,且与直线
∶
交于点A.
(1)请写出A(
________,________
),B(________,________),C
(
________,________
).
(2)若D是线段OA上的一点,且△COD的面积为12,求直线CD的函数表达式.
(3)在(2)的条件下,设P是射线CD上的点,在平面内存在点Q,使以O、C、P、Q为顶点的四边形是菱形,请直接写出Q点的坐标.
25.如图1,有一张矩形纸片ABCD,AB=4,BC=8,点M,N分别在矩形的边AD,BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN于点Q,连接CM.
(1)求证:四边形CMPN是菱形;
(2)当P,A重合时,如图2,求MN的长;
(3)设△PQM的面积为S,求S的取值范围.
答案解析部分
一、单选题
1.【答案】
C
解:对角线互相垂直平分的四边形是菱形,故A选项错误;有一条对角线平分对角的四边形不一定是菱形,故B选项错误;菱形的对角线是互相垂直平分的四边形,故C选项正确;菱形的对角线不一定相等,故D选项错误.
2.【答案】
A
解:由题意知AC=6,BD=8,则菱形的面积S=×6×8=24,
∵菱形对角线互相垂直平分,
∴△AOB为直角三角形,AO=3,BO=4,
∴AB==5,
∴菱形的高h==
.
故选A.
3.【答案】
C
解:∵四边形ABCD为平行四边形,∴∠1=∠4,∠2=∠3,∵AC平分∠DAB
,
∴∠1=∠2,∴∠1=∠3,∴AD=DC
,
四边形ABCD为菱形,∴四边形ABCD的周长=4×2=8.
4.【答案】
C
解:∵在
ABCD中,对角线AC与BD相交于点O,
∴AO=CO,∠AFO=∠CEO,
∵在△AFO和△CEO中,∠AFO=∠CEO,∠
FOA=∠EOC,AO=CO,
∴△AFO≌△CEO(AAS),
∴FO=EO,
∴四边形AECF平行四边形,
∵EF⊥AC,
∴平行四边形AECF是菱形,
故答案为:C.
5.【答案】
B
解:过F做FH⊥AB且交于点H,连接EH,
在△ACF与△AHF中
∵AF平分∠CAB交CD于E
,
又∵AF=AF,
∴△ACF≌△AHF,
∴AC=AH,
同理在△ACE与△AHE中,△ACE≌△AHE,
可知CE=EH,∠ACE=∠AHE,
在Rt△ACD中,∠CAD+∠ACD=90°,
在Rt△ABC中,∠CAB+∠B=90°,
又∵∠CAD与∠CAB为同一角,
∴∠ACD=∠B,
∴∠AHE=∠B,
∴EH∥BC,
∵CD⊥AB,FH⊥AB,
∴CD∥FH,
∴四边形CEHF为菱形,四边形EGBH为平行四边形,
∴CF=EH=,EH=GB,
∴CF=GB.
故答案为:B.
6.【答案】
B
解:连接DE、BD,
由菱形的对角线互相垂直平分,可得B、D关于AC对称,连接PB.则PD=PB,
∴PE+PB=PE+PD=DE,
即DE就是PE+PB的最小值,
∵∠BAD=60°,AD=AB,
∴△ABD是等边三角形,
∵AE=BE,
∴DE⊥AB(等腰三角形三线合一的性质),
在Rt△ADE中,DE=
.
故选:B.
7.【答案】
B
解:连接PA,如图所示:
∵四边形ABCD是菱形,
∴∠ADP=∠CDP=∠ADC=36°,BD所在直线是菱形的对称轴,
∴PA=PC,
∵AD的垂直平分线交对角线BD于点P,
∴PA=PD,
∴PD=PC,
∴∠PCD=∠CDP=36°,
∴∠CPB=∠PCD+∠CDP=72°;
故选:B.
8.【答案】
C
直角三角形斜边上的中线
解:如图,连接FC,
①
∵F为Rt△ACB的斜边AB的中点,
∴FC=FA,E点在AC的垂直平分线上,
又∵△EAC为等边三角形,
∴AE=EC,F点在AC的垂直平分线上,
∴EF为AC的垂直平分线,
则EF⊥AC,符合题意;
②∠DAC=∠DAB+∠BAC=60°+30°=90°,即DA⊥AC,
又∵EF⊥AC,
∴EF∥BC,
∵F为AB的中点,△ABD为等边三角形,
∴DF⊥AB,
∵∠EAB=∠EAC+∠CAB=60°+30°=90°,即AE⊥AB,
∴AE∥DF,
∴四边形AEFD为平行四边形(两边分别平行的四边形是平行四边形);
在△AFD中,由于∠DFA=90°,
∴AD>FD,?
∴
四边形ADFE不是菱形?,不符合题意;
③?∵△ABD为等边三角形,
∴AD=AB,
∵AF=BF,
∴AF=AB=AD,
∵四边形ADFE为平行四边形,
∴FG=AG,
∴AG=AF=×AD=AD,符合题意;
④∵?AF=BF,
∠DFB=∠EAF=90°(已证),
∵四边形AEFD为平行四边形,
∴AD=EF,
又∵AD=AB,
∴EF=AB,
∴
△DBF≌△EFA(HL),符合题意.
故答案为:C.
9.【答案】
D
解:由作图知AC=AD=BC=BD,
∴四边形ACBD是菱形,
∴AB平分∠CAD、CD平分∠ACB、AB⊥CD,
不能判断AB=CD,
故答案为:D.
10.【答案】
B
解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
∴∠BAG=∠EDG,△ABO≌△BCO≌△CDO≌△AOD,
∵CD=DE,
∴AB=DE,
在△ABG和△DEG中,
,
∴△ABG≌△DEG(AAS),
∴AG=DG,
∴OG是△ACD的中位线,
∴OG=
CD=
AB,
∴①正确;
∵AB∥CE,AB=DE,
∴四边形ABDE是平行四边形,
∵∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴OD=AG,四边形ABDE是菱形,
④正确;
∴AD⊥BE,
由菱形的性质得:△ABG≌△BDG≌△DEG,
在△ABG和△DCO中,
,
∴△ABG≌△DCO(SAS),
∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,
∴②不正确;
∵OB=OD,AG=DG,
∴OG是△ABD的中位线,
∴OG∥AB,OG=
AB,
∴△GOD∽△ABD,△ABF∽△OGF,
∴△GOD的面积=
△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
∴△AFG的面积=△OGF的面积的2倍,
又∵△GOD的面积=△AOG的面积=△BOG的面积,
∴S四边形ODGF=S△ABF;
③正确;
正确的是①③④.
故选B.
二、填空题
11.【答案】12
【解析】解:由题意,知:S菱形=×4×6=12.
故答案为12.
12.【答案】
8
解:由题意得,四边形
?为菱形
?
?
在
?中,
?
?.
13.【答案】
24
解:连接AE,∵四边形ABCD为平行四边形
∴AD∥BC,AD=BC
∵BF为∠ABE的平分线,∴∠FBE=∠AFB,∴四边形ABEF为平行四边形
∵AB=AF,
∴根据勾股定理,即可得到AE=2=8.
∴四边形ABEF的面积=×AE×BF=24.
14.【答案】50
解:在菱形ABCD中,
AB∥CD,∴∠CDO=∠AED=50°,
CD=CB,∠BCO=∠DCO,
∴在△BCO和△DCO中,
,
∴△BCO≌△DCO(SAS),
∴∠CBO=∠CDO=50°.
故答案为50.
15.【答案】
20
解:∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,
∴BD=DF=
AC,
∴四边形BGFD是菱形,
设GF=x,则AF=13-x,AC=2x,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2
,
即(13-x)2+62=(2x)2
,
解得:x=5,
故四边形BDFG的周长=4GF=20.
16.【答案】
四条边相等的四边形为菱形,菱形的对边平行.
解:由作法得:BA=BC=AD=CD,
所以四边形ABCD为菱形,
所以AD∥BC.
故答案为:四条边相等的四边形为菱形,菱形的对边平行.
三、解答题
17.【答案】
证明:∵D、E分别是AB、AC的中点,∴DE∥BC,BC=2DE.∵CF∥BE,∴四边形BCFE是平行四边形,∵BE=2DE,BC=2DE,∴BE=BC,∴平行四边形BCFE是菱形.
18.【答案】
(1)证明:∵AF∥BD,∴∠AFE=∠DBE,∵E是AD中点,∴AE=ED,在△BDE和△FAE中,
,
∴△AFE≌△DBE.
(2)证明:连接CF.∵△AFE≌△DBE,∴AF=BD∵∠BAC=90°,BD=CD,∴AD=DC=DB,∴AF∥CD,AF=DC,∴四边形ADCF是平行四边形,∵DA=CD,∴四边形ADCF是菱形.(3)∵S△ABC=×AB×AC=10,∵四边形ADCF是菱形,BD=DC,S△ABC=2S△ADC
,
∴S菱形ADCF=2S△ADC=10.
19.【答案】
(1)解:根据旋转可得∠CAE=100°,AC=AE,
∵∠AEC+∠ACE+∠CAE=180°,
∴∠AEC=(180°﹣100°)=40°;
(2)证明:∵∠BAD=∠CAE=100°,AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=40°.
∵∠BAE=∠BAD+∠DAE=140°,
∴∠BFE=360°﹣∠BAE﹣∠ABD﹣∠AEC=140°,
∴∠BAE=∠BFE,
∴四边形ABFE是平行四边形,
∵AB=AE,
∴平行四边形ABFE是菱形.
20.【答案】
(1)证明:∵PQ垂直平分BE,
∴PB=PE,OB=OE.
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,
,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵PB=PE,
∴四边形BPEQ是菱形;
(2)解:∵四边形ABCD是矩形,
∴∠A=90°,
∴AE
8
设PE=y,则AP=8﹣y,BP=PE=y,
在Rt△ABP中,62+(8﹣y)2=y2
,
解得
,
∴BP=PE
,
∵四边形BPEQ是菱形,
∴
,
在Rt△EOP中,
,
∴
.
21.【答案】
(1)证明:∵四边形ABCD为正方形,
∴∠EAB=∠FCB=90°,AB=BC,
在△AEB与△CFB中,
,
∴△ABE≌△CBF(SAS),
∴BE=BF,
∵EG∥BF,FG∥BE,
∴四边形BEGF是平行四边形,
∴四边形BEGF是菱形
(2)解:∵四边形BEGF是菱形,
∴EB=BF=FG=GE,
∵AD=3AE=6,
∴AE=2,AB=AD=6,
∴BE=
=2
,
∴四边形BEGF的周长为:4×2
=8
.
22.【答案】
(1)证明:证明:在Rt△ABC中,∠BAC=
,D是BC的中点,
∴AD=
BC=DC=BD,
∵AF∥BC,
∴∠DBE=∠AFE,
又∵E是AD中点,
∴ED=EA,
又∠BED=∠FEA,
∴△BDE≌△FAE(AAS);
(2)证明:由(1)知AF=BD,即AF=DC,
∴AF∥DC,AF=DC,
∴四边形ADCF是平行四边形,
又∵AD=DC,
∴四边形ADCF是菱形
(3)解:(解法一)连接DF,
∵AF
DC,BD=CD,
∴AF
BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∴
;
(解法二)在Rt△ABC中,AC=4,AB=5,
∴BC=
,
设BC边上的高为
,
则
,
∴
,
∴
23.【答案】
(1)证明:∵PQ垂直平分BE,
∴PB=PE,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,
,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵QB=QE,
∴四边形BPEQ是菱形;
(2)解:∵AB=6,F是AB的中点,
∴BF=3.
∵四边形BPEQ是菱形,
∴OB=OE.
又∵F是AB的中点,
∴OF是△BAE的中位线,
∴AE∥OF且OF=
AE.
∴∠BFO=∠A=90°.
在Rt△FOB中,OB=
=5,
∴BE=10.
设菱形的边长为x,则AP=8﹣x.
在Rt△APB中,BP2=AB2+AP2
,
即x2=62+(8﹣x)2
,
解得:x=
,
∴BQ=
,
∴菱形BPEQ的面积=BQ×AB=
×6=
.
24.【答案】
(1)6;3;12;0;0;6
(2)解:设D
???
?????????????????????????????????????????????????????????
由(1)可知C(0,6)
∴OC=6
又∵
∴
解得:
∴D(4,2)????????????????????????
??????????????????????????????????????????????????????????????
设直线CD的解析式为
???
∴
解得:
∴直线CD的解析式为
(3)
解:(1)∵两个直线交于点A
∴-x+6=x,解得x=6,代入y=3,∴点A的坐标为(6,3)
令y=0,x=12,∴点B的坐标为(12,0)
令x=0,y=6,则点C的坐标为(0,6)
(2)解:设D(x,x)?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
由(1)可知C(0,6)
∴OC=6
又∵
三角形COD的面积为12
∴
S△COD=×6×x=12
解得:
x=4
∴D(4,2)
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
??
设直线CD的解析式为y=kx+b(k≠0,k,b为常数)?
?
?
∴?
解得:
k=-1,b=6
∴直线CD的解析式为
y=-x+6
(3)如图所示,分三种情况考虑:
(i)当四边形OP1Q1C为菱形时,由∠COP1=90°,得到四边形OP1Q1C为正方形,此时QP1=OP1=OC=6,即Q1(6,6);
(ii)当四边形OP2CQ2为菱形时,由C坐标为(0,6),得到Q2纵坐标为3,
把y=3代入直线OQ2解析式y=-x中,得:x=-3,此
时Q2(-3,3);
(ii)当四边形OQ3P3C为菱形时,则有OQ3=OC=CP3=P3Q3=6,此时Q3(
,-
),
综上,点Q的坐标是(6,6)或(-3,3)或(
,-
),
25.【答案】
(1)证明:∵四边形ABCD是矩形,
∴PM∥CN,
∴∠PMN=∠MNC.
由折叠的性质可知∠MNC=∠PNM,NC=NP,
∴∠PMN=∠PNM.
∴PM=PN.
∵NC=NP,
∴PM=CN.
∵MP∥CN,
∴四边形CMPN是平行四边形.
∵NC=NP,
∴四边形CMPN是菱形
(2)解:当点P与点A重合时,设BN=x,则AN=NC=8-x.
在Rt△ABN中,AB2+BN2=AN2
,
即42+x2=(8-x)2
,
解得x=3.
∴CN=8-3=5.
∵四边形CMPN是菱形,AC=
,
∴MN=
.
(3)解:∵四边形CMPN是菱形,
∴S=
∵S菱形CMPN=CN·AB,
∴当点M与点D重合时,如图,此时CN最短,菱形CMPN的面积最小,
∵
,四边形CMPN是菱形,
∴四边形CMPN是正方形,
则S最小=
;
当点P与点A重合时,CN最长,菱形CMPN的面积最大,
则S最大=
×5×4=5.
∴S的取值范围是
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
初中数学苏科版八年级下册
9.4
菱形的判定及性质
同步训练
一、单选题(本题共10题,每题3分,共30分)
1.下列命题中,真命题是( ).
A.?对角线相等且互相垂直的四边形是菱形???????????????B.?有一条对角线平分对角的四边形是菱形
C.?菱形是对角线互相垂直平分的四边形??????????????????D.?菱形的对角线相等
2.菱形的两条对角线的长分别为6和8,则菱形的高为(
)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
3.如图,在平行四边形ABCD中,AC平分∠DAB
,
AB=2,则平行四边形ABCD的周长为( ).?
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?12
4.如图,在
ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF.则四边形AECF是(???
)
A.?梯形????????????????????????????????????B.?矩形????????????????????????????????????C.?菱形????????????????????????????????????D.?正方形
5.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,AF平分∠CAB交CD于E,交CB于F,且EG∥AB交CB于G,则CF与GB的大小关系是(
??)
A.?CF>GB?????????????????????????????B.?GB=CF?????????????????????????????C.?CF<GB?????????????????????????????D.?无法确定
6.如图,在菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为( )
A.?1?????????????????????????????????????????B.??????????????????????????????????????????C.?2?????????????????????????????????????????D.?
7.如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB的度数是( )
A.?108°?????????????????????????????????????B.?72°?????????????????????????????????????C.?90°?????????????????????????????????????D.?100°
8.如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G.连接EF,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.则正确结论的序号是(???
)
A.?①③??????????????????????????????????B.?②④??????????????????????????????????C.?①③④??????????????????????????????????D.?②③④
9.如图,已知线段AB,分别以A,B为圆心,大于
AB同样长为半径画弧,两弧交于点C,D,连接AC,AD,BC,BD,CD,则下列说法错误的是(?
)
A.?AB平分∠CAD???????????????????????B.?CD平分∠ACB???????????????????????C.?AB⊥CD???????????????????????D.?AB=CD
10.如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE,分别交AC,AD于点F、G,连结OG,则下列结论:
①OG=
AB;②图中与△EGD全等的三角形共有5个;③由点A、B、D、E构成的四边形是菱形;④S四边形ODGF=S△ABF
,
其中正确的结论是(??
)
A.?①③?????????????????????????????????B.?①③④?????????????????????????????????C.?①②③?????????????????????????????????D.?②③④
二、填空题(本题共6题,每题2分,共12分)
11.菱形两条对角线长分别是4和6,则这个菱形的面积为________?.
12.如图,平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为________.
13.如图,在平行四边形ABCD中,∠ABC的平分线BF交AD于点F,FE∥AB.若AB=5,BF=6,则四边形ABEF的面积为________?。
14.如图,在菱形ABCD中,点E是AB上的一点,连接DE交AC于点O,连接BO,且∠AED=50°,则∠CBO=________?度.
15.如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则四边形BDFG的周长为________.
16.在数学课上,老师提出如下问题:
尺规作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A.
求作:l的平行线,使它经过点A.
小云的作法如下:(1)在直线l上任取一点B;(2)以B为圆心,BA长为半径作弧,交直线l于点C;(3)分别以A、C为圆心,BA长为半径作弧,两弧相交于点D;(4)作直线AD.直线AD即为所求.
小云作图的依据是________.
三、解答题(本题共9题,共88分)
17.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE
,
过点C作CF∥BE交DE的延长线于F
.
求证:四边形BCFE是菱形.
18.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F
(1)求证:△AEF≌△DEB;
(2)证明:四边形ADCF是菱形;
(3)若AB=4,AC=5,求菱形ADCF的面积.
?
19.如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD和CE,BD与CE交于点F.
(1)∠AEC的度数;
(2)求证:四边形ABFE是菱形.
20.如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,BE=10,求PQ的长.
21.如图,点E,F分别在正方形ABCD的边DA,DC延长线上,且AE=CF,连接BE,BF,过点E作EG∥BF,过点F作FG∥BE,EG,FG交于点G.
(1)求证:四边形BEGF是菱形;
(2)若AD=3AE=6,求四边形BEGF的周长.
22.在Rt△ABC中,∠BAC=
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD
的面积.
23.如图,在矩形ABCD中,E是AD边上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、QE
(1)求证:四边形BPEQ是菱形:
(2)若AB=6,F是AB中点,OF=4,求菱形BPEQ的面积.
24.如图,在平面直角坐标系中,直线
∶
分别与
轴、
轴交于点B、C,且与直线
∶
交于点A.
(1)请写出A(
________,________
),B(________,________),C
(
________,________
).
(2)若D是线段OA上的一点,且△COD的面积为12,求直线CD的函数表达式.
(3)在(2)的条件下,设P是射线CD上的点,在平面内存在点Q,使以O、C、P、Q为顶点的四边形是菱形,请直接写出Q点的坐标.
25.如图1,有一张矩形纸片ABCD,AB=4,BC=8,点M,N分别在矩形的边AD,BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN于点Q,连接CM.
(1)求证:四边形CMPN是菱形;
(2)当P,A重合时,如图2,求MN的长;
(3)设△PQM的面积为S,求S的取值范围.
答案解析部分
一、单选题
1.【答案】
C
解:对角线互相垂直平分的四边形是菱形,故A选项错误;有一条对角线平分对角的四边形不一定是菱形,故B选项错误;菱形的对角线是互相垂直平分的四边形,故C选项正确;菱形的对角线不一定相等,故D选项错误.
2.【答案】
A
解:由题意知AC=6,BD=8,则菱形的面积S=×6×8=24,
∵菱形对角线互相垂直平分,
∴△AOB为直角三角形,AO=3,BO=4,
∴AB==5,
∴菱形的高h==
.
故选A.
3.【答案】
C
解:∵四边形ABCD为平行四边形,∴∠1=∠4,∠2=∠3,∵AC平分∠DAB
,
∴∠1=∠2,∴∠1=∠3,∴AD=DC
,
四边形ABCD为菱形,∴四边形ABCD的周长=4×2=8.
4.【答案】
C
解:∵在
ABCD中,对角线AC与BD相交于点O,
∴AO=CO,∠AFO=∠CEO,
∵在△AFO和△CEO中,∠AFO=∠CEO,∠
FOA=∠EOC,AO=CO,
∴△AFO≌△CEO(AAS),
∴FO=EO,
∴四边形AECF平行四边形,
∵EF⊥AC,
∴平行四边形AECF是菱形,
故答案为:C.
5.【答案】
B
解:过F做FH⊥AB且交于点H,连接EH,
在△ACF与△AHF中
∵AF平分∠CAB交CD于E
,
又∵AF=AF,
∴△ACF≌△AHF,
∴AC=AH,
同理在△ACE与△AHE中,△ACE≌△AHE,
可知CE=EH,∠ACE=∠AHE,
在Rt△ACD中,∠CAD+∠ACD=90°,
在Rt△ABC中,∠CAB+∠B=90°,
又∵∠CAD与∠CAB为同一角,
∴∠ACD=∠B,
∴∠AHE=∠B,
∴EH∥BC,
∵CD⊥AB,FH⊥AB,
∴CD∥FH,
∴四边形CEHF为菱形,四边形EGBH为平行四边形,
∴CF=EH=,EH=GB,
∴CF=GB.
故答案为:B.
6.【答案】
B
解:连接DE、BD,
由菱形的对角线互相垂直平分,可得B、D关于AC对称,连接PB.则PD=PB,
∴PE+PB=PE+PD=DE,
即DE就是PE+PB的最小值,
∵∠BAD=60°,AD=AB,
∴△ABD是等边三角形,
∵AE=BE,
∴DE⊥AB(等腰三角形三线合一的性质),
在Rt△ADE中,DE=
.
故选:B.
7.【答案】
B
解:连接PA,如图所示:
∵四边形ABCD是菱形,
∴∠ADP=∠CDP=∠ADC=36°,BD所在直线是菱形的对称轴,
∴PA=PC,
∵AD的垂直平分线交对角线BD于点P,
∴PA=PD,
∴PD=PC,
∴∠PCD=∠CDP=36°,
∴∠CPB=∠PCD+∠CDP=72°;
故选:B.
8.【答案】
C
直角三角形斜边上的中线
解:如图,连接FC,
①
∵F为Rt△ACB的斜边AB的中点,
∴FC=FA,E点在AC的垂直平分线上,
又∵△EAC为等边三角形,
∴AE=EC,F点在AC的垂直平分线上,
∴EF为AC的垂直平分线,
则EF⊥AC,符合题意;
②∠DAC=∠DAB+∠BAC=60°+30°=90°,即DA⊥AC,
又∵EF⊥AC,
∴EF∥BC,
∵F为AB的中点,△ABD为等边三角形,
∴DF⊥AB,
∵∠EAB=∠EAC+∠CAB=60°+30°=90°,即AE⊥AB,
∴AE∥DF,
∴四边形AEFD为平行四边形(两边分别平行的四边形是平行四边形);
在△AFD中,由于∠DFA=90°,
∴AD>FD,?
∴
四边形ADFE不是菱形?,不符合题意;
③?∵△ABD为等边三角形,
∴AD=AB,
∵AF=BF,
∴AF=AB=AD,
∵四边形ADFE为平行四边形,
∴FG=AG,
∴AG=AF=×AD=AD,符合题意;
④∵?AF=BF,
∠DFB=∠EAF=90°(已证),
∵四边形AEFD为平行四边形,
∴AD=EF,
又∵AD=AB,
∴EF=AB,
∴
△DBF≌△EFA(HL),符合题意.
故答案为:C.
9.【答案】
D
解:由作图知AC=AD=BC=BD,
∴四边形ACBD是菱形,
∴AB平分∠CAD、CD平分∠ACB、AB⊥CD,
不能判断AB=CD,
故答案为:D.
10.【答案】
B
解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
∴∠BAG=∠EDG,△ABO≌△BCO≌△CDO≌△AOD,
∵CD=DE,
∴AB=DE,
在△ABG和△DEG中,
,
∴△ABG≌△DEG(AAS),
∴AG=DG,
∴OG是△ACD的中位线,
∴OG=
CD=
AB,
∴①正确;
∵AB∥CE,AB=DE,
∴四边形ABDE是平行四边形,
∵∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴OD=AG,四边形ABDE是菱形,
④正确;
∴AD⊥BE,
由菱形的性质得:△ABG≌△BDG≌△DEG,
在△ABG和△DCO中,
,
∴△ABG≌△DCO(SAS),
∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,
∴②不正确;
∵OB=OD,AG=DG,
∴OG是△ABD的中位线,
∴OG∥AB,OG=
AB,
∴△GOD∽△ABD,△ABF∽△OGF,
∴△GOD的面积=
△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
∴△AFG的面积=△OGF的面积的2倍,
又∵△GOD的面积=△AOG的面积=△BOG的面积,
∴S四边形ODGF=S△ABF;
③正确;
正确的是①③④.
故选B.
二、填空题
11.【答案】12
【解析】解:由题意,知:S菱形=×4×6=12.
故答案为12.
12.【答案】
8
解:由题意得,四边形
?为菱形
?
?
在
?中,
?
?.
13.【答案】
24
解:连接AE,∵四边形ABCD为平行四边形
∴AD∥BC,AD=BC
∵BF为∠ABE的平分线,∴∠FBE=∠AFB,∴四边形ABEF为平行四边形
∵AB=AF,
∴根据勾股定理,即可得到AE=2=8.
∴四边形ABEF的面积=×AE×BF=24.
14.【答案】50
解:在菱形ABCD中,
AB∥CD,∴∠CDO=∠AED=50°,
CD=CB,∠BCO=∠DCO,
∴在△BCO和△DCO中,
,
∴△BCO≌△DCO(SAS),
∴∠CBO=∠CDO=50°.
故答案为50.
15.【答案】
20
解:∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,
∴BD=DF=
AC,
∴四边形BGFD是菱形,
设GF=x,则AF=13-x,AC=2x,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2
,
即(13-x)2+62=(2x)2
,
解得:x=5,
故四边形BDFG的周长=4GF=20.
16.【答案】
四条边相等的四边形为菱形,菱形的对边平行.
解:由作法得:BA=BC=AD=CD,
所以四边形ABCD为菱形,
所以AD∥BC.
故答案为:四条边相等的四边形为菱形,菱形的对边平行.
三、解答题
17.【答案】
证明:∵D、E分别是AB、AC的中点,∴DE∥BC,BC=2DE.∵CF∥BE,∴四边形BCFE是平行四边形,∵BE=2DE,BC=2DE,∴BE=BC,∴平行四边形BCFE是菱形.
18.【答案】
(1)证明:∵AF∥BD,∴∠AFE=∠DBE,∵E是AD中点,∴AE=ED,在△BDE和△FAE中,
,
∴△AFE≌△DBE.
(2)证明:连接CF.∵△AFE≌△DBE,∴AF=BD∵∠BAC=90°,BD=CD,∴AD=DC=DB,∴AF∥CD,AF=DC,∴四边形ADCF是平行四边形,∵DA=CD,∴四边形ADCF是菱形.(3)∵S△ABC=×AB×AC=10,∵四边形ADCF是菱形,BD=DC,S△ABC=2S△ADC
,
∴S菱形ADCF=2S△ADC=10.
19.【答案】
(1)解:根据旋转可得∠CAE=100°,AC=AE,
∵∠AEC+∠ACE+∠CAE=180°,
∴∠AEC=(180°﹣100°)=40°;
(2)证明:∵∠BAD=∠CAE=100°,AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=40°.
∵∠BAE=∠BAD+∠DAE=140°,
∴∠BFE=360°﹣∠BAE﹣∠ABD﹣∠AEC=140°,
∴∠BAE=∠BFE,
∴四边形ABFE是平行四边形,
∵AB=AE,
∴平行四边形ABFE是菱形.
20.【答案】
(1)证明:∵PQ垂直平分BE,
∴PB=PE,OB=OE.
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,
,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵PB=PE,
∴四边形BPEQ是菱形;
(2)解:∵四边形ABCD是矩形,
∴∠A=90°,
∴AE
8
设PE=y,则AP=8﹣y,BP=PE=y,
在Rt△ABP中,62+(8﹣y)2=y2
,
解得
,
∴BP=PE
,
∵四边形BPEQ是菱形,
∴
,
在Rt△EOP中,
,
∴
.
21.【答案】
(1)证明:∵四边形ABCD为正方形,
∴∠EAB=∠FCB=90°,AB=BC,
在△AEB与△CFB中,
,
∴△ABE≌△CBF(SAS),
∴BE=BF,
∵EG∥BF,FG∥BE,
∴四边形BEGF是平行四边形,
∴四边形BEGF是菱形
(2)解:∵四边形BEGF是菱形,
∴EB=BF=FG=GE,
∵AD=3AE=6,
∴AE=2,AB=AD=6,
∴BE=
=2
,
∴四边形BEGF的周长为:4×2
=8
.
22.【答案】
(1)证明:证明:在Rt△ABC中,∠BAC=
,D是BC的中点,
∴AD=
BC=DC=BD,
∵AF∥BC,
∴∠DBE=∠AFE,
又∵E是AD中点,
∴ED=EA,
又∠BED=∠FEA,
∴△BDE≌△FAE(AAS);
(2)证明:由(1)知AF=BD,即AF=DC,
∴AF∥DC,AF=DC,
∴四边形ADCF是平行四边形,
又∵AD=DC,
∴四边形ADCF是菱形
(3)解:(解法一)连接DF,
∵AF
DC,BD=CD,
∴AF
BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∴
;
(解法二)在Rt△ABC中,AC=4,AB=5,
∴BC=
,
设BC边上的高为
,
则
,
∴
,
∴
23.【答案】
(1)证明:∵PQ垂直平分BE,
∴PB=PE,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,
,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵QB=QE,
∴四边形BPEQ是菱形;
(2)解:∵AB=6,F是AB的中点,
∴BF=3.
∵四边形BPEQ是菱形,
∴OB=OE.
又∵F是AB的中点,
∴OF是△BAE的中位线,
∴AE∥OF且OF=
AE.
∴∠BFO=∠A=90°.
在Rt△FOB中,OB=
=5,
∴BE=10.
设菱形的边长为x,则AP=8﹣x.
在Rt△APB中,BP2=AB2+AP2
,
即x2=62+(8﹣x)2
,
解得:x=
,
∴BQ=
,
∴菱形BPEQ的面积=BQ×AB=
×6=
.
24.【答案】
(1)6;3;12;0;0;6
(2)解:设D
???
?????????????????????????????????????????????????????????
由(1)可知C(0,6)
∴OC=6
又∵
∴
解得:
∴D(4,2)????????????????????????
??????????????????????????????????????????????????????????????
设直线CD的解析式为
???
∴
解得:
∴直线CD的解析式为
(3)
解:(1)∵两个直线交于点A
∴-x+6=x,解得x=6,代入y=3,∴点A的坐标为(6,3)
令y=0,x=12,∴点B的坐标为(12,0)
令x=0,y=6,则点C的坐标为(0,6)
(2)解:设D(x,x)?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
由(1)可知C(0,6)
∴OC=6
又∵
三角形COD的面积为12
∴
S△COD=×6×x=12
解得:
x=4
∴D(4,2)
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
??
设直线CD的解析式为y=kx+b(k≠0,k,b为常数)?
?
?
∴?
解得:
k=-1,b=6
∴直线CD的解析式为
y=-x+6
(3)如图所示,分三种情况考虑:
(i)当四边形OP1Q1C为菱形时,由∠COP1=90°,得到四边形OP1Q1C为正方形,此时QP1=OP1=OC=6,即Q1(6,6);
(ii)当四边形OP2CQ2为菱形时,由C坐标为(0,6),得到Q2纵坐标为3,
把y=3代入直线OQ2解析式y=-x中,得:x=-3,此
时Q2(-3,3);
(ii)当四边形OQ3P3C为菱形时,则有OQ3=OC=CP3=P3Q3=6,此时Q3(
,-
),
综上,点Q的坐标是(6,6)或(-3,3)或(
,-
),
25.【答案】
(1)证明:∵四边形ABCD是矩形,
∴PM∥CN,
∴∠PMN=∠MNC.
由折叠的性质可知∠MNC=∠PNM,NC=NP,
∴∠PMN=∠PNM.
∴PM=PN.
∵NC=NP,
∴PM=CN.
∵MP∥CN,
∴四边形CMPN是平行四边形.
∵NC=NP,
∴四边形CMPN是菱形
(2)解:当点P与点A重合时,设BN=x,则AN=NC=8-x.
在Rt△ABN中,AB2+BN2=AN2
,
即42+x2=(8-x)2
,
解得x=3.
∴CN=8-3=5.
∵四边形CMPN是菱形,AC=
,
∴MN=
.
(3)解:∵四边形CMPN是菱形,
∴S=
∵S菱形CMPN=CN·AB,
∴当点M与点D重合时,如图,此时CN最短,菱形CMPN的面积最小,
∵
,四边形CMPN是菱形,
∴四边形CMPN是正方形,
则S最小=
;
当点P与点A重合时,CN最长,菱形CMPN的面积最大,
则S最大=
×5×4=5.
∴S的取值范围是
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
