2.3平行线的性质 同步习题 (Word版 含解析)
文档属性
| 名称 | 2.3平行线的性质 同步习题 (Word版 含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 122.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 00:00:00 | ||
图片预览


文档简介
2.3平行线的性质 同步习题
一.选择题
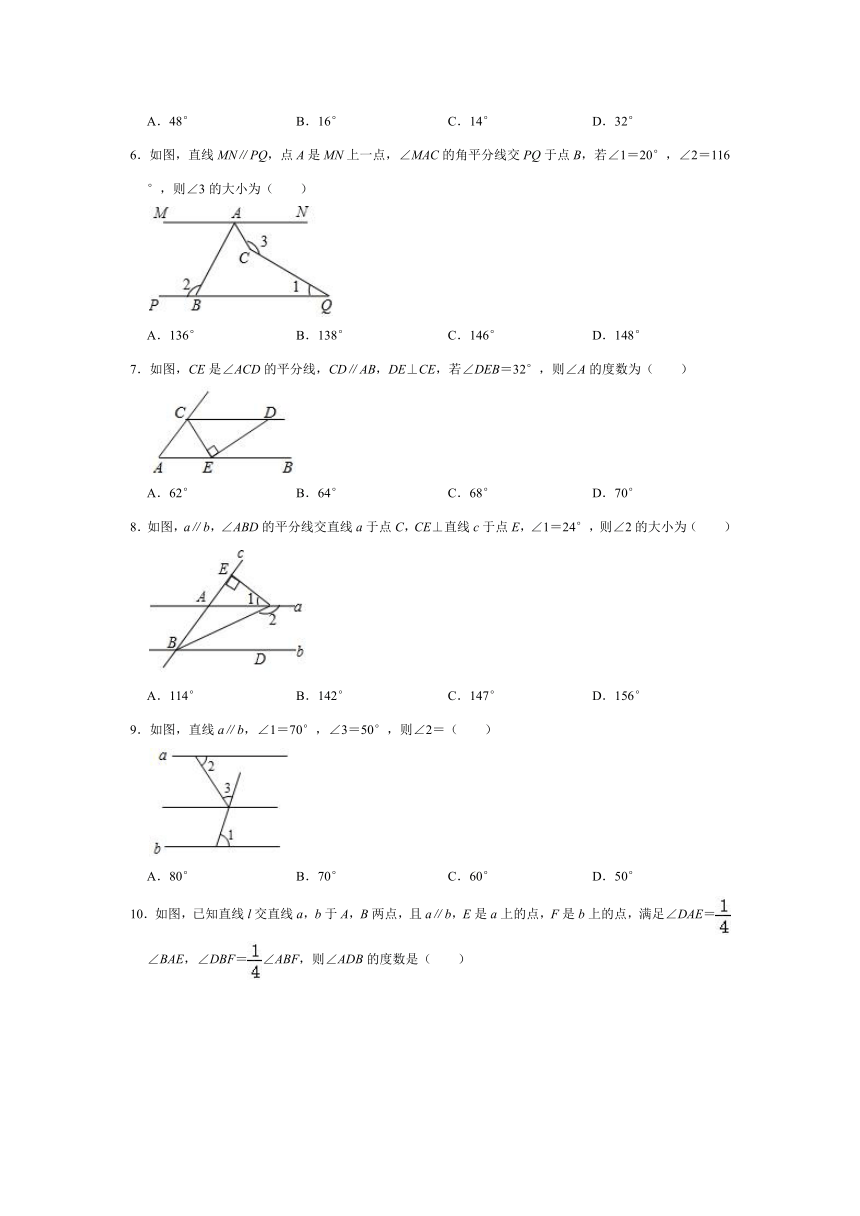
1.如图,已知AB∥CD,CE平分∠ACD,交AB于点B,∠ABE=150°,则∠A为( )
A.110° B.120° C.135° D.150°
2.如图,若AD∥BC,则下列结论正确的是( )
A.∠1=∠3 B.∠2=∠4 C.∠1=∠2 D.∠2=∠3
3.下列各图形中均有直线m∥n,则能使结论∠A=∠1﹣∠2成立的是( )
A. B.
C. D.
4.如图,AB∥CD,∠A=30°,∠F=40°,则∠C=( )
A.65° B.70° C.75° D.80°
5.将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置,如果∠CED=46°,那么∠BAF的度数为( )
A.48° B.16° C.14° D.32°
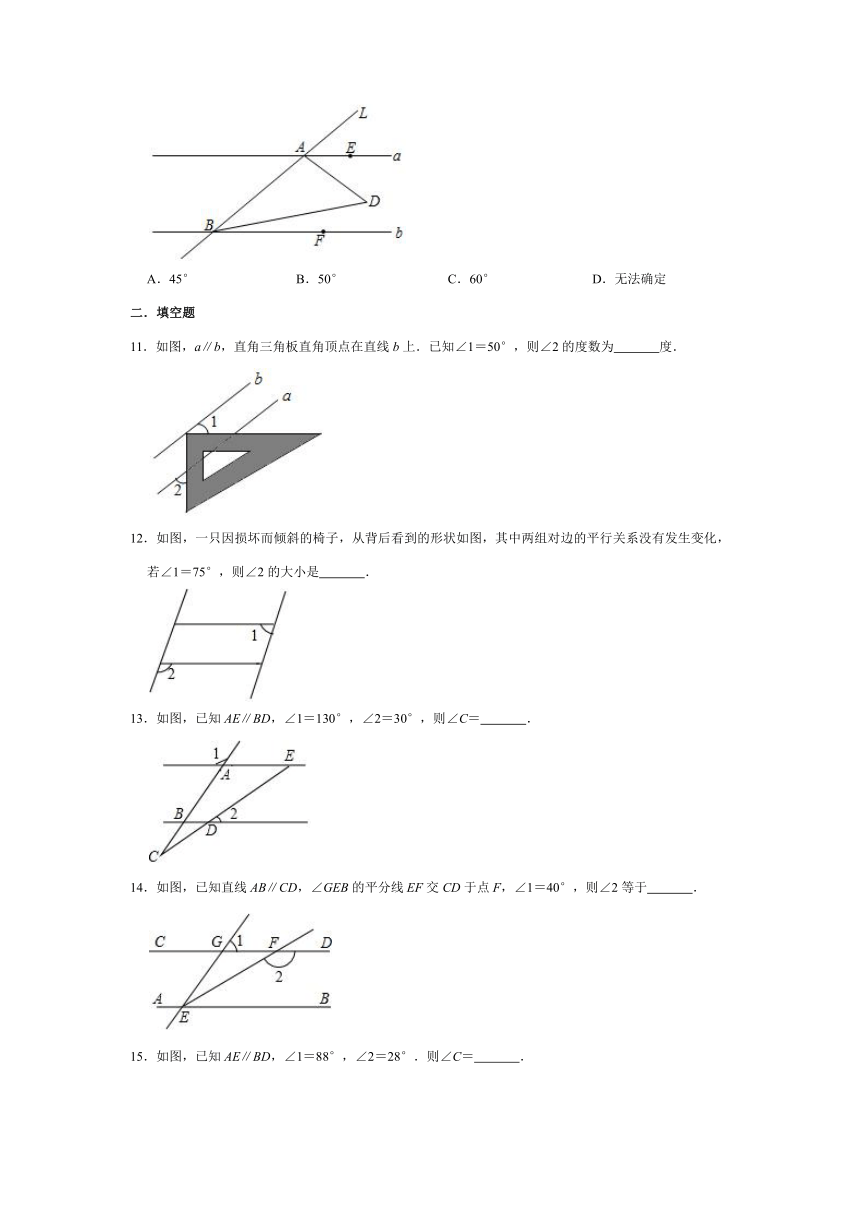
6.如图,直线MN∥PQ,点A是MN上一点,∠MAC的角平分线交PQ于点B,若∠1=20°,∠2=116°,则∠3的大小为( )
A.136° B.138° C.146° D.148°
7.如图,CE是∠ACD的平分线,CD∥AB,DE⊥CE,若∠DEB=32°,则∠A的度数为( )
A.62° B.64° C.68° D.70°
8.如图,a∥b,∠ABD的平分线交直线a于点C,CE⊥直线c于点E,∠1=24°,则∠2的大小为( )
A.114° B.142° C.147° D.156°
9.如图,直线a∥b,∠1=70°,∠3=50°,则∠2=( )
A.80° B.70° C.60° D.50°
10.如图,已知直线l交直线a,b于A,B两点,且a∥b,E是a上的点,F是b上的点,满足∠DAE=∠BAE,∠DBF=∠ABF,则∠ADB的度数是( )
A.45° B.50° C.60° D.无法确定
二.填空题
11.如图,a∥b,直角三角板直角顶点在直线b上.已知∠1=50°,则∠2的度数为 度.
12.如图,一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的大小是 .
13.如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C= .
14.如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=40°,则∠2等于 .
15.如图,已知AE∥BD,∠1=88°,∠2=28°.则∠C= .
三.解答题
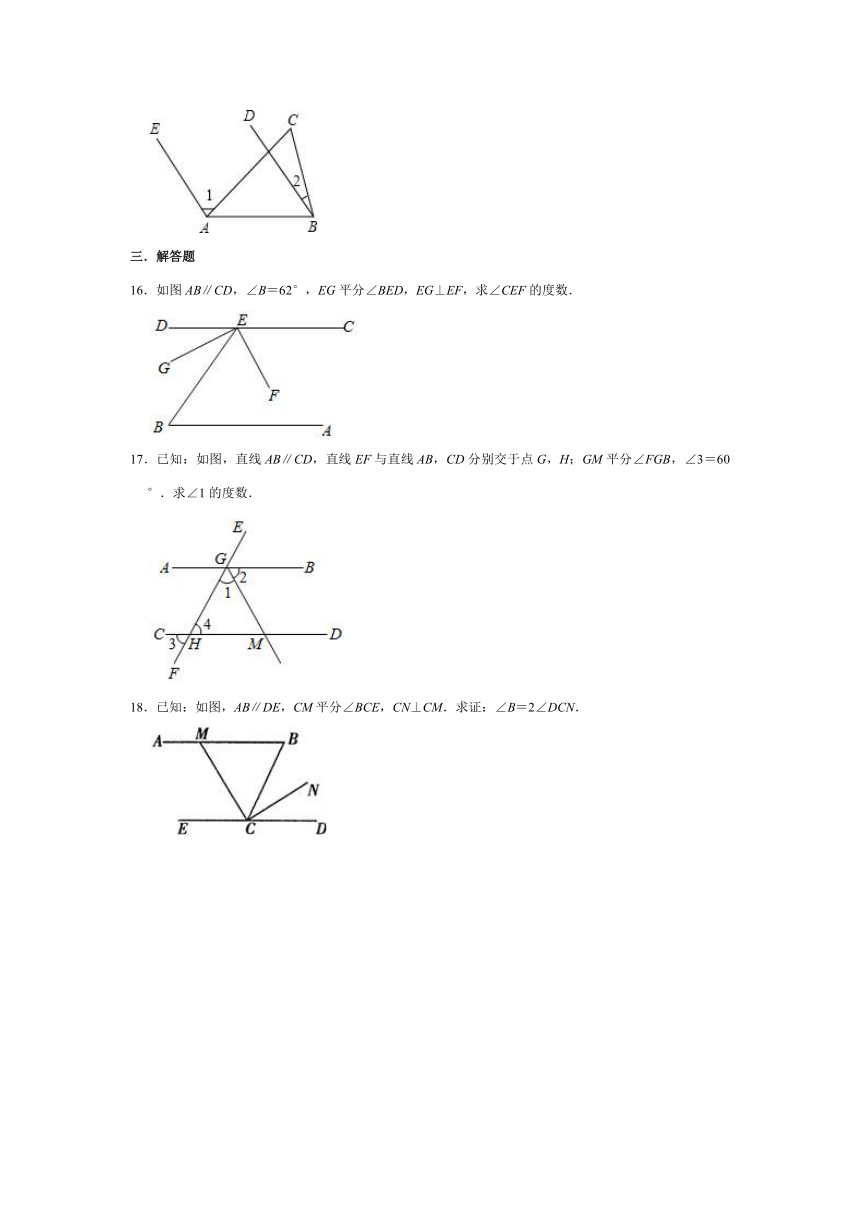
16.如图AB∥CD,∠B=62°,EG平分∠BED,EG⊥EF,求∠CEF的度数.
17.已知:如图,直线AB∥CD,直线EF与直线AB,CD分别交于点G,H;GM平分∠FGB,∠3=60°.求∠1的度数.
18.已知:如图,AB∥DE,CM平分∠BCE,CN⊥CM.求证:∠B=2∠DCN.
参考答案
一.选择题
1.解:∵∠ABE=150°,
∴∠ABC=30°,
又∵AB∥CD,
∴∠ABC=∠BCD=30°,
∵CE平分∠ACD,
∴∠ACD=2∠BCD=60°,
又∵AB∥CD,
∴∠A+∠ACD=180°,
∴∠A=180°﹣∠ACD=180°﹣60°=120°.
故选:B.
2.解:∵AD∥BC,
∴∠3=∠1,
故选:A.
3.解:A、∵m∥n,
∴∠2=∠1+∠A,
∴∠A=∠2﹣∠1,不符合题意;
B、∵m∥n,
∴∠1=∠2+∠A,
∴∠A=∠1﹣∠2,符合题意;
C、∵m∥n,
∴∠1+∠2+∠A=360°,
∴∠A=360°﹣∠2﹣∠1,不符合题意;
D、∵m∥n,
∴∠A=∠1+∠2,不符合题意;
故选:B.
4.解:∵∠A=30°,∠F=40°,
∴∠FEB=∠A+∠F=30°+40°=70°,
∵AB∥CD,
∴∠C=∠FEB=70°,
故选:B.
5.解:∵DE∥AF,
∴∠CED=∠EAF=46°,
∵∠BAC=90°﹣30°=60°,
∴∠BAF=∠BAC﹣∠EAF=60°﹣46°=14°,
故选:C.
6.解:延长QC交AB于D,
∵MN∥PQ,
∴∠2+∠MAB=180°,
∵∠2=116°,
∴∠MAB=180°﹣116°=64°,
∵AB平分∠MAC,
∴∠MAB=∠BAC=64°,
△BDQ中,∠BDQ=∠2﹣∠1=116°﹣20°=96°,
∴∠ADC=180°﹣96°=84°,
△ADC中,∠3=∠BAC+∠ADC=64°+84°=148°.
故选:D.
7.解:∵CE是∠ACD的平分线,
∴∠ACE=∠DCE,
∵DE⊥CE,
∴∠CDE+∠DCE=90°,∠BED+∠AEC=90°,
∵∠DEB=32°,
∴∠AEC=90°﹣∠DEB=90°﹣32°=58°,
∵CD∥AB,
∴∠CDE=∠BED,
∴∠DCE=∠AEC,
∴∠ACE=∠AEC,
∴∠A=180°﹣2∠AEC=180°﹣2×58°=64°.
故选:B.
8.解:∵∠1=24°,CE⊥直线c于点E,
∴∠EAC=90°﹣∠1=90°﹣24°=66°,
∵a∥b,
∴∠EAC=∠ABD=66°,
∵∠ABD的平分线交直线a于点C,
∴∠CBD=,
∴∠2=180°﹣∠CBD=180°﹣33°=147°,
故选:C.
9.解:如右图所示,
∵a∥b,
∴∠1=∠4,
∴∠1=70°,
∴∠4=70°,
∵∠3=50°,∠2+∠3+∠4=180°,
∴∠2=180°﹣∠3﹣∠4=180°﹣50°﹣70°=60°,
故选:C.
10.解:∵a∥b,
∴∠EAB+∠ABF=180°,
∵∠DAE=∠BAE,∠DBF=∠ABF,
∴∠DAB+∠ABD=×180°=135°,
∴∠ADB=180°﹣(∠DAB+∠ABD)=180°﹣135°=45°,
故选:A.
二.填空题
11.解:如图,
∵∠1+∠3=90°,
∴∠3=90°﹣∠1=90°﹣50°=40°,
∵a∥b,
∴∠2=∠3=40°,
故答案为:40.
12.解:如图,∵AD∥BC,∠1=75°,
∴∠3=∠1=75°,
∵AB∥CD,
∴∠2=180°﹣∠3=180°﹣75°=105°.
故答案为:105°.
13.解:∵AE∥BD,∠1=130°,∠2=30°,
∴∠CBD=∠1=130°.
∵∠BDC=∠2,
∴∠BDC=30°.
在△BCD中,∠CBD=130°,∠BDC=30°,
∴∠C=180°﹣130°﹣30°=20°.
故答案为:20°.
14.解:∵AB∥CD,
∴∠BEG=∠1=40°,
∵EF是∠GEB的平分线,
∴∠BEF=∠BEG=×40°=20°,
∵AB∥CD,
∴∠2=180°﹣∠BEF=180°﹣20°=160°.
故答案为:160°.
15.解:∵AE∥BD,
∴∠1=∠3=88°,
∵∠3=∠2+∠C,
∴∠C=∠3﹣∠2=88°﹣28°=60°,
故答案为:60°.
三.解答题
16.解:∵AB∥CD,∠B=62°,
∴∠BED=∠B=62°,
∵EG平分∠BED,
∴∠DEG=∠BED=31°,
∵EG⊥EF,
∴∠FEG=90°,
∴∠DEG+∠CEF=90°,
∴∠CEF=90°﹣∠DEG=90°﹣31°=59°.
17.解:∵EF与CD交于点H,(已知),
∴∠3=∠4.(对顶角相等),
∵∠3=60°,(已知),
∴∠4=60°.(等量代换),
∵AB∥CD,EF与AB,CD交于点G,H,(已知),
∴∠4+∠FGB=180°.(两直线平行,同旁内角互补),
∴∠FGB=120°.
∵GM平分∠FGB,(已知),
∴∠1=60°.(角平分线的定义).
18.证明:∵AB∥DE,
∴∠B+∠BCE=180°,∠B=∠BCD,
∵CM平分∠BCE,
∴∠1=∠2,
∵CN⊥CM,
∴∠2+∠3=90°,∠1+∠4=90°,
∴∠3=∠4,
∵∠3+∠4=∠BCD,
∴∠B=2∠DCN.
一.选择题
1.如图,已知AB∥CD,CE平分∠ACD,交AB于点B,∠ABE=150°,则∠A为( )
A.110° B.120° C.135° D.150°
2.如图,若AD∥BC,则下列结论正确的是( )
A.∠1=∠3 B.∠2=∠4 C.∠1=∠2 D.∠2=∠3
3.下列各图形中均有直线m∥n,则能使结论∠A=∠1﹣∠2成立的是( )
A. B.
C. D.
4.如图,AB∥CD,∠A=30°,∠F=40°,则∠C=( )
A.65° B.70° C.75° D.80°
5.将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置,如果∠CED=46°,那么∠BAF的度数为( )
A.48° B.16° C.14° D.32°
6.如图,直线MN∥PQ,点A是MN上一点,∠MAC的角平分线交PQ于点B,若∠1=20°,∠2=116°,则∠3的大小为( )
A.136° B.138° C.146° D.148°
7.如图,CE是∠ACD的平分线,CD∥AB,DE⊥CE,若∠DEB=32°,则∠A的度数为( )
A.62° B.64° C.68° D.70°
8.如图,a∥b,∠ABD的平分线交直线a于点C,CE⊥直线c于点E,∠1=24°,则∠2的大小为( )
A.114° B.142° C.147° D.156°
9.如图,直线a∥b,∠1=70°,∠3=50°,则∠2=( )
A.80° B.70° C.60° D.50°
10.如图,已知直线l交直线a,b于A,B两点,且a∥b,E是a上的点,F是b上的点,满足∠DAE=∠BAE,∠DBF=∠ABF,则∠ADB的度数是( )
A.45° B.50° C.60° D.无法确定
二.填空题
11.如图,a∥b,直角三角板直角顶点在直线b上.已知∠1=50°,则∠2的度数为 度.
12.如图,一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的大小是 .
13.如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C= .
14.如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=40°,则∠2等于 .
15.如图,已知AE∥BD,∠1=88°,∠2=28°.则∠C= .
三.解答题
16.如图AB∥CD,∠B=62°,EG平分∠BED,EG⊥EF,求∠CEF的度数.
17.已知:如图,直线AB∥CD,直线EF与直线AB,CD分别交于点G,H;GM平分∠FGB,∠3=60°.求∠1的度数.
18.已知:如图,AB∥DE,CM平分∠BCE,CN⊥CM.求证:∠B=2∠DCN.
参考答案
一.选择题
1.解:∵∠ABE=150°,
∴∠ABC=30°,
又∵AB∥CD,
∴∠ABC=∠BCD=30°,
∵CE平分∠ACD,
∴∠ACD=2∠BCD=60°,
又∵AB∥CD,
∴∠A+∠ACD=180°,
∴∠A=180°﹣∠ACD=180°﹣60°=120°.
故选:B.
2.解:∵AD∥BC,
∴∠3=∠1,
故选:A.
3.解:A、∵m∥n,
∴∠2=∠1+∠A,
∴∠A=∠2﹣∠1,不符合题意;
B、∵m∥n,
∴∠1=∠2+∠A,
∴∠A=∠1﹣∠2,符合题意;
C、∵m∥n,
∴∠1+∠2+∠A=360°,
∴∠A=360°﹣∠2﹣∠1,不符合题意;
D、∵m∥n,
∴∠A=∠1+∠2,不符合题意;
故选:B.
4.解:∵∠A=30°,∠F=40°,
∴∠FEB=∠A+∠F=30°+40°=70°,
∵AB∥CD,
∴∠C=∠FEB=70°,
故选:B.
5.解:∵DE∥AF,
∴∠CED=∠EAF=46°,
∵∠BAC=90°﹣30°=60°,
∴∠BAF=∠BAC﹣∠EAF=60°﹣46°=14°,
故选:C.
6.解:延长QC交AB于D,
∵MN∥PQ,
∴∠2+∠MAB=180°,
∵∠2=116°,
∴∠MAB=180°﹣116°=64°,
∵AB平分∠MAC,
∴∠MAB=∠BAC=64°,
△BDQ中,∠BDQ=∠2﹣∠1=116°﹣20°=96°,
∴∠ADC=180°﹣96°=84°,
△ADC中,∠3=∠BAC+∠ADC=64°+84°=148°.
故选:D.
7.解:∵CE是∠ACD的平分线,
∴∠ACE=∠DCE,
∵DE⊥CE,
∴∠CDE+∠DCE=90°,∠BED+∠AEC=90°,
∵∠DEB=32°,
∴∠AEC=90°﹣∠DEB=90°﹣32°=58°,
∵CD∥AB,
∴∠CDE=∠BED,
∴∠DCE=∠AEC,
∴∠ACE=∠AEC,
∴∠A=180°﹣2∠AEC=180°﹣2×58°=64°.
故选:B.
8.解:∵∠1=24°,CE⊥直线c于点E,
∴∠EAC=90°﹣∠1=90°﹣24°=66°,
∵a∥b,
∴∠EAC=∠ABD=66°,
∵∠ABD的平分线交直线a于点C,
∴∠CBD=,
∴∠2=180°﹣∠CBD=180°﹣33°=147°,
故选:C.
9.解:如右图所示,
∵a∥b,
∴∠1=∠4,
∴∠1=70°,
∴∠4=70°,
∵∠3=50°,∠2+∠3+∠4=180°,
∴∠2=180°﹣∠3﹣∠4=180°﹣50°﹣70°=60°,
故选:C.
10.解:∵a∥b,
∴∠EAB+∠ABF=180°,
∵∠DAE=∠BAE,∠DBF=∠ABF,
∴∠DAB+∠ABD=×180°=135°,
∴∠ADB=180°﹣(∠DAB+∠ABD)=180°﹣135°=45°,
故选:A.
二.填空题
11.解:如图,
∵∠1+∠3=90°,
∴∠3=90°﹣∠1=90°﹣50°=40°,
∵a∥b,
∴∠2=∠3=40°,
故答案为:40.
12.解:如图,∵AD∥BC,∠1=75°,
∴∠3=∠1=75°,
∵AB∥CD,
∴∠2=180°﹣∠3=180°﹣75°=105°.
故答案为:105°.
13.解:∵AE∥BD,∠1=130°,∠2=30°,
∴∠CBD=∠1=130°.
∵∠BDC=∠2,
∴∠BDC=30°.
在△BCD中,∠CBD=130°,∠BDC=30°,
∴∠C=180°﹣130°﹣30°=20°.
故答案为:20°.
14.解:∵AB∥CD,
∴∠BEG=∠1=40°,
∵EF是∠GEB的平分线,
∴∠BEF=∠BEG=×40°=20°,
∵AB∥CD,
∴∠2=180°﹣∠BEF=180°﹣20°=160°.
故答案为:160°.
15.解:∵AE∥BD,
∴∠1=∠3=88°,
∵∠3=∠2+∠C,
∴∠C=∠3﹣∠2=88°﹣28°=60°,
故答案为:60°.
三.解答题
16.解:∵AB∥CD,∠B=62°,
∴∠BED=∠B=62°,
∵EG平分∠BED,
∴∠DEG=∠BED=31°,
∵EG⊥EF,
∴∠FEG=90°,
∴∠DEG+∠CEF=90°,
∴∠CEF=90°﹣∠DEG=90°﹣31°=59°.
17.解:∵EF与CD交于点H,(已知),
∴∠3=∠4.(对顶角相等),
∵∠3=60°,(已知),
∴∠4=60°.(等量代换),
∵AB∥CD,EF与AB,CD交于点G,H,(已知),
∴∠4+∠FGB=180°.(两直线平行,同旁内角互补),
∴∠FGB=120°.
∵GM平分∠FGB,(已知),
∴∠1=60°.(角平分线的定义).
18.证明:∵AB∥DE,
∴∠B+∠BCE=180°,∠B=∠BCD,
∵CM平分∠BCE,
∴∠1=∠2,
∵CN⊥CM,
∴∠2+∠3=90°,∠1+∠4=90°,
∴∠3=∠4,
∵∠3+∠4=∠BCD,
∴∠B=2∠DCN.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
