1.4角平分线课件（16张）

(共16张PPT)
第1课时
角平分线
1、什么叫角平分线？
如果一条射线把一个角分成两个相等的角，
那么这条射线叫角的平分线。
角平分线上的点到角的两边的距离相等
条件：一个点在一个角的平分线上
结论：它到角的两边的距离相等
已知：如图OC是∠AOB的平分线，点P在
OC上，PD
⊥OA
，PE
⊥OB.
求证：PD=PE.
A
O
B
P
E
D
C
2、你还记得角平分线上的点有什么性质吗?你是怎样得到的？
你能证明这一结论吗?
老师期望:你能写出规范的证明过程.
用符号语言表示为：
A
O
B
P
E
D
1
2
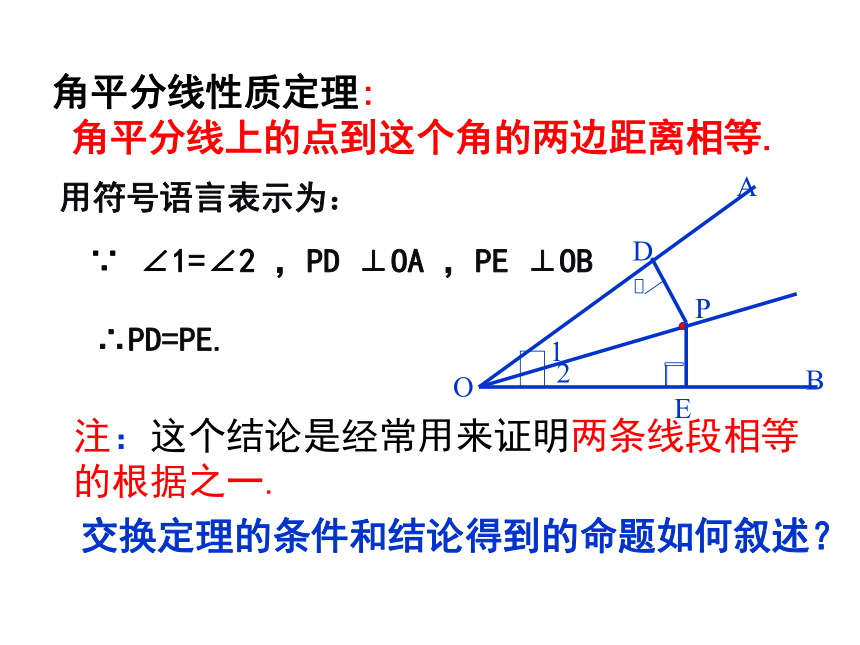
∴PD=PE.
交换定理的条件和结论得到的命题如何叙述？
注：这个结论是经常用来证明两条线段相等的根据之一.
角平分线性质定理:
角平分线上的点到这个角的两边距离相等.
∵
∠1=∠2
，PD
⊥OA
，PE
⊥OB
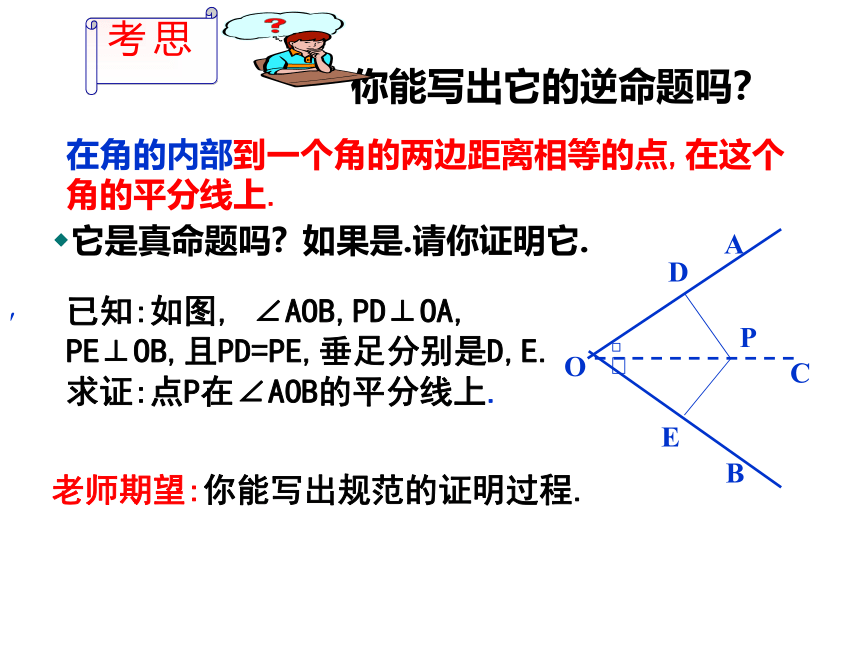
你能写出它的逆命题吗？
′
思考
在角的内部到一个角的两边距离相等的点,在这个角的平分线上.
它是真命题吗?
如果是.请你证明它.
已知:如图,
∠AOB,PD⊥OA,
PE⊥OB,且PD=PE,垂足分别是D,E.
求证:点P在∠AOB的平分线上.
O
C
B
A
P
D
E
老师期望:你能写出规范的证明过程.
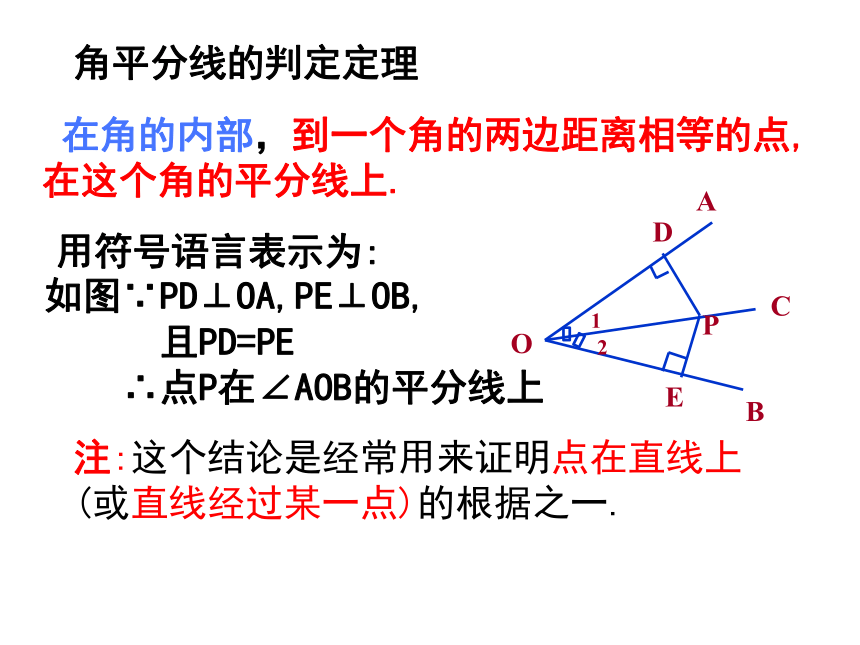
在角的内部，到一个角的两边距离相等的点,在这个角的平分线上.
用符号语言表示为:
如图∵PD⊥OA,PE⊥OB,
且PD=PE
∴点P在∠AOB的平分线上
注:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.
角平分线的判定定理
1
2
A
B
D
E
P
O
C
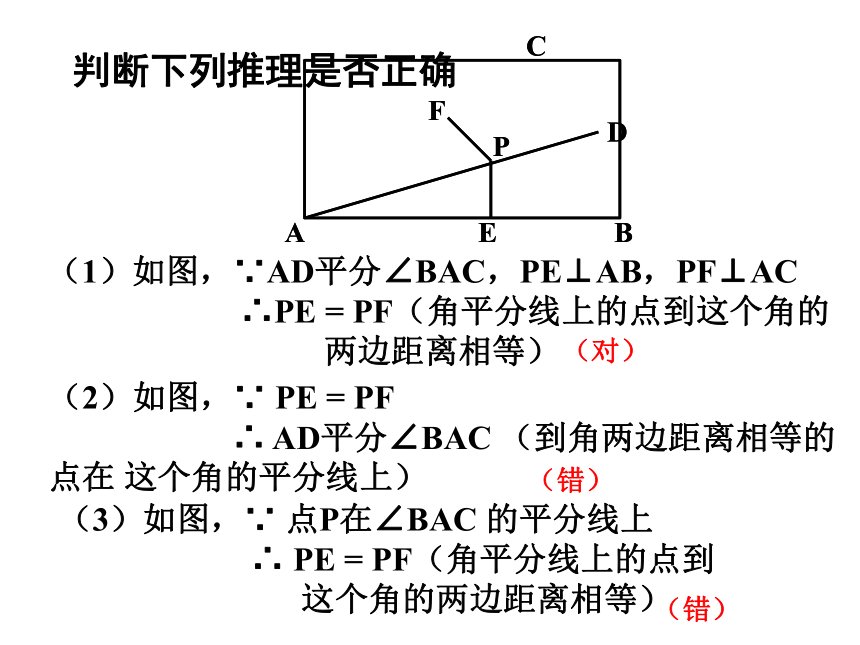
判断下列推理是否正确
（1）如图，∵AD平分∠BAC，PE⊥AB，PF⊥AC
∴PE
=
PF（角平分线上的点到这个角的
两边距离相等）
（2）如图，∵
PE
=
PF
∴
AD平分∠BAC
（到角两边距离相等的
点在
这个角的平分线上）
（3）如图，∵
点P在∠BAC
的平分线上
∴
PE
=
PF（角平分线上的点到
这个角的两边距离相等）
A
B
C
D
E
F
P
（对）
（错）
（错）
A
B
C
D
E
F
P
判断下列推理是否正确
A
B
C
D
E
F
P
A
B
C
D
E
F
P
（4）如图，∵
PE⊥AB，PF⊥AC
∴
AD平分∠BAC（到角两边距离相等的点在这个角的平分线上）
（错）
（5）如图∵
PE⊥AB，PF⊥AC，PE
=
PF
∴点P在∠BAC
的平分线上（到角两边距离相等的点在这个角的平分线上）
（对）
随堂演练
1
如图，在△ABC中，∠BAC=60°，点D在BC上，AD=10,DE⊥AB，DF⊥AC，垂足分别为E，F，且DE=DF，求DE的长
解：∵DE⊥AB，DF⊥AC，垂足分别为E，F，
且DE=DF，
∴AD平分∠BAC（在一个角的内部，到角的两边距离相等的点在这个角的平分线上）
又∵∠BAC=60°，
∴∠BAD=30°，
在Rt△ADE中，∠ADE=90°，AD=10
∴DE=
AD=
×10=5（在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半）
随堂练习
1
如图,AD,AE分别是△ABC中∠A的内角平分线外角平分线,它们有什么关系?
老师期望:
你能说出结论并能证明它.
E
D
A
B
C
F
1.角平分线的性质定理：
在角平分线上的点到角的两边的距离相等
2.角平分线的判定定理：
在角的内部，到一个角的两边的距离相等的点，在这个角平分线上。
4.角平分线的性质定理是证明角相等、线段相等的新途径.角平分线的判定定理是证明点在直线上(或直线经过某一点)的根据之一.
3.性质定理和判定定理的关系
点在角平分线上
点到角两边的距离相等
课堂小结
布置作业
6：作业布置
课堂作业：习题1.9第1，2，3,4题．
家庭作业：学习之友p15-16
课堂作业：习题1.9第1，2，3,4题．
家庭作业：学习之友p15-16