5.3 平行线的性质课时训练(含答案)
文档属性
| 名称 | 5.3 平行线的性质课时训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 961.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 00:00:00 | ||
图片预览


文档简介
1102360010363200第五章 相交线与平行线
5.3 平行线的性质1252220011303000课时训练
1.下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有一个角是60°的等腰三角形是等边三角形
C.有一组邻边相等的四边形是菱形
D.对角线相等的四边形是矩形
2.下列命题中,为假命题是( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.两组对角分别相等的四边形是平行四边形
D.对角线相等的四边形是平行四边形
3.下列命题中,其逆命题是假命题的是( )
A.两直线平行,内错角相等
B.对顶角相等
C.在一个三角形中,相等的角所对的边也相等
D.到角的两边距离相等的点在这个角的平分线上
4.下面命题:①同位角相等;②对顶角相等;③若x2=y2,则x=y;④互补的角是邻补角.其中正确命题有( )
A.1 B.2 C.3 D.4
5.如图,若AD∥BC,则下列结论正确的是( )
A.∠1=∠3 B.∠2=∠4 C.∠1=∠2 D.∠2=∠3
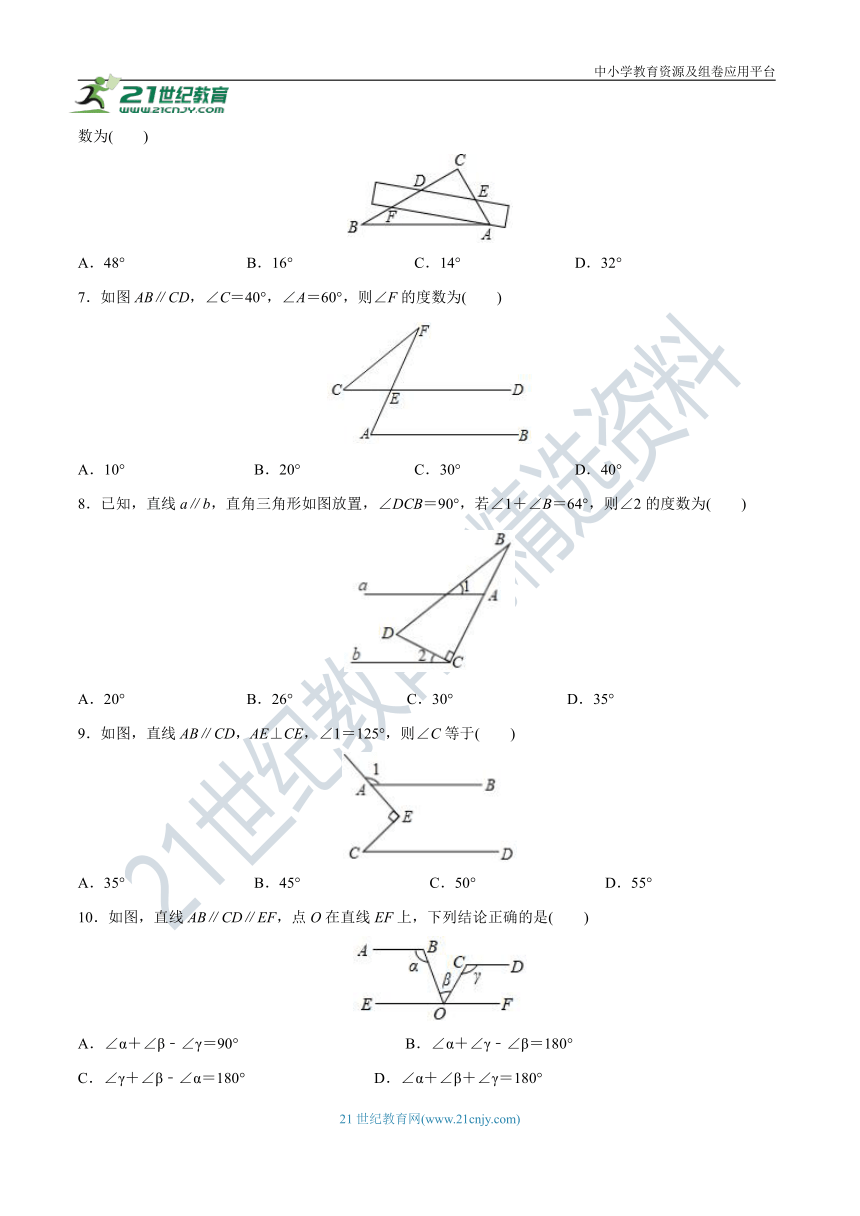
6.将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置,如果∠CED=46°,那么∠BAF的度数为( )
A.48° B.16° C.14° D.32°
7.如图AB∥CD,∠C=40°,∠A=60°,则∠F的度数为( )
A.10° B.20° C.30° D.40°
8.已知,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠B=64°,则∠2的度数为( )
A.20° B.26° C.30° D.35°
9.如图,直线AB∥CD,AE⊥CE,∠1=125°,则∠C等于( )
A.35° B.45° C.50° D.55°
10.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90° B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180° D.∠α+∠β+∠γ=180°
11.如图,将三角尺的直角顶点放在直尺的一边上,若∠1=60°15′,则∠2的大小为( )
A.60°15′ B.39°45′ C.29°85′ D.29°45′
12.如图,已知AD⊥BC,FG⊥BC,∠BAC=90°,DE∥AC.则结论:①FG∥AD;②DE平分ADB;③∠B=∠ADE;④∠CFG+∠BDE=90°.正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
13.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AB∥CE,且∠ADC=∠B;④AB∥CE且∠BCD=∠BAD;其中能推出BC∥AD的条件为( )
A.①② B.②④ C.②③ D.②③④
14.命题“如果a3=b3,那么a=b”是 .(填“真命题”或“假命题”)
15.命题“全等三角形的对应角相等”的逆命题是 .
16.“等角的补角相等”的条件是 ,结论是 .
17.如图,AB∥CD,∠A=25°,∠C=70°,则∠E= .
18.如图,AB∥CD∥EF,且CF平分∠AFE,若∠C=20°,则∠A的度数是 .
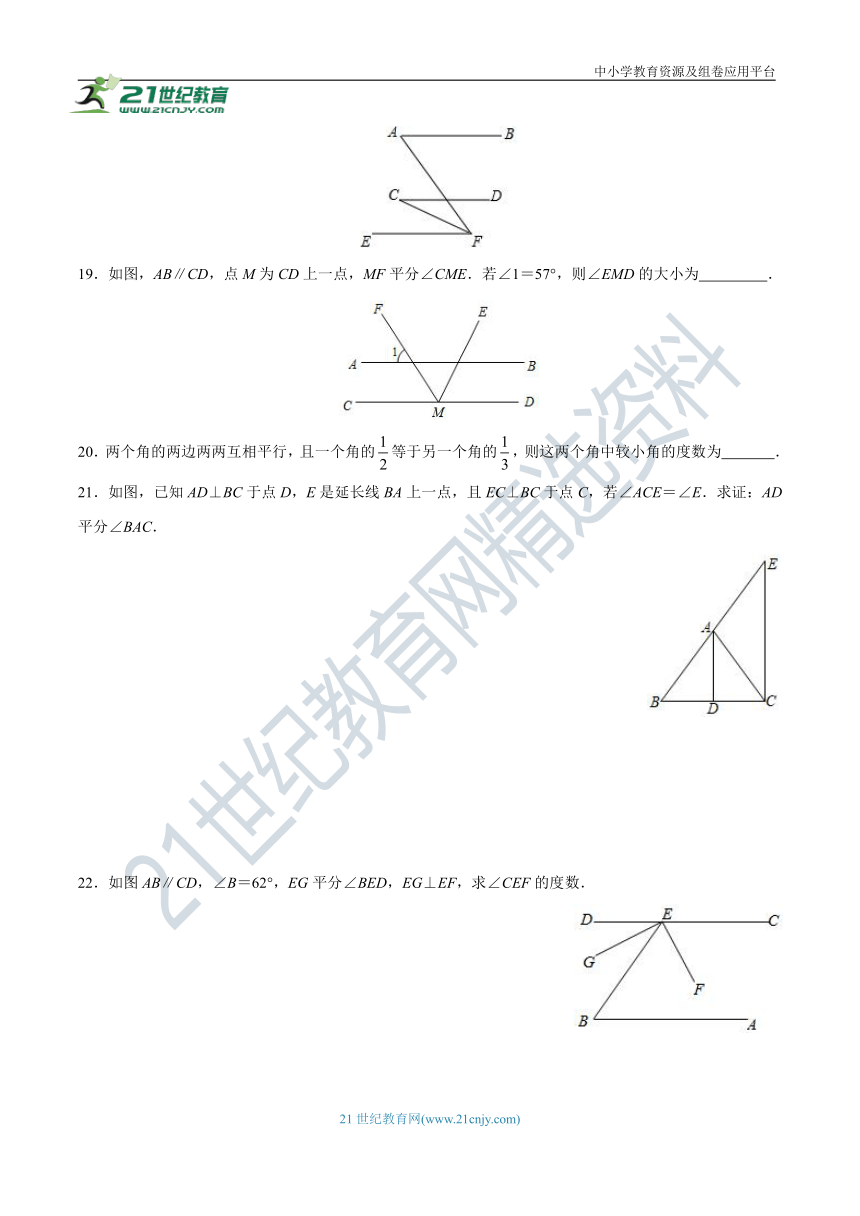
19.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为 .
20.两个角的两边两两互相平行,且一个角的false等于另一个角的false,则这两个角中较小角的度数为 .
21.如图,已知AD⊥BC于点D,E是延长线BA上一点,且EC⊥BC于点C,若∠ACE=∠E.求证:AD平分∠BAC.
22.如图AB∥CD,∠B=62°,EG平分∠BED,EG⊥EF,求∠CEF的度数.
23.如图,已知AB∥CD,E是直线AB上的一点,CE平分∠ACD,射线CF⊥CE,∠1=32°,
(1)求∠ACE的度数;
(2)若∠2=58°,求证:CF∥AG.
24.如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
25.如图,已知直线AB∥CD,直线EF与直线AB,CD分别交于点G,H;GM平分∠FGB,∠3=60°.求∠1的度数.
答案
1. B 【解析】选项A,一组对边平行,另一组对边相等的四边形不一定是平行四边形,原命题是假命题;选项B,有一个角是60°的等腰三角形是等边三角形,是真命题;选项C,有一组邻边相等的平行四边形是菱形,原命题是假命题;选项D,对角线相等的平行四边形是矩形.原命题是假命题. 故选B.
2. D 【解析】两组对边分别平行的四边形是平行四边形,是真命题,故选项A不符合题意;两组对边分别相等的四边形是平行四边形,是真命题,故选项B不符合题意;两组对角分别相等的四边形是平行四边形,是真命题,故选项C不符合题意;对角线互相平分的四边形是平行四边形,原命题是假命题,故选项D符合题意. 故选D.
3. B 【解析】两直线平行,内错角相等的逆命题是内错角相等,两直线平行,逆命题是真命题,故选项A不符合题意;对顶角相等的逆命题是相等的两个角是对顶角,逆命题是假命题,故选项B符合题意;在一
个三角形中,相等的角所对的边也相等的逆命题是在一个三角形中,相等的边所对的角也相等,逆命题是真命题,故选项C不符合题意;到角的两边距离相等的点在这个角的平分线上的逆命题是角的平分线上的点到角的两边距离相等,逆命题是真命题,故选项D不符合题意. 故选B.
4. A 【解析】①两直线平行,同位角相等,原命题是假命题;②对顶角相等,是真命题;③若x2=y2,则x=y或x=﹣y,原命题是假命题;④互补的角不一定是邻补角,原命题是假命题.故选A.
5. A 【解析】∵AD∥BC,∴∠3=∠1,故选A.
6. C 【解析】∵DE∥AF,∴∠CED=∠EAF=46°,∵∠BAC=90°﹣30°=60°,∴∠BAF=∠BAC﹣∠EAF=60°﹣46°=14°,故选C.
7. B 【解析】∵AB∥CD,∴∠A=∠FED=60°,∵∠FED=∠C+∠F,∴∠F=∠FED﹣∠C=60°﹣40°=20°,故选B.
8. B 【解析】∵∠1+∠B=64°,∴∠3=∠1+∠B=64°,∵a∥b,∴∠3+∠ACD+∠2=180°,∴∠2=180°﹣∠ACD﹣∠3=180°﹣90°﹣64°=26°,故选B.
9. A 【解析】过点E作EF∥AB,则EF∥CD,如图所示.∵EF∥AB,∴∠BAE=∠AEF.∵EF∥CD,∴∠C=∠CEF.∵AE⊥CE,∴∠AEC=90°,即∠AEF+∠CEF=90°,∴∠BAE+∠C=90°.∵∠1=125°,∠1+∠BAE=180°,∴∠BAE=180°﹣125°=55°,∴∠C=90°﹣55°=35°.故选A.
10. B 【解析】∵AB∥EF,∴∠α=∠BOF,∵CD∥EF,∴∠γ+∠COF=180°,∵∠BOF=∠COF+∠β,∴∠γ+∠α﹣∠β=180°,故选B.
11. D 【解析】如图,由直尺两边平行,可得∠1=∠3=60°15',∴∠2=90°﹣∠3=90°﹣60°15'=29°45',故选D.
12. C 【解析】∵AD⊥BC,FG⊥BC,∴∠FGD=∠ADB=90°,∴FG∥AD,故①正确;∵DE∥AC,∠BAC=90°,∴DE⊥AB,不能证明DE为∠ADB的平分线,故②错误;∵AD⊥BC,∴∠B+∠BAD=90°,∵DE⊥AB,∴∠BAD+∠ADE=90°,∴∠B=∠ADE,故③正确;∵∠BAC=90°,DE⊥AB,∴∠CFG+∠C=90°,∠BDE+∠B=90°,∠C+∠B=90°,∴∠CFG+∠BDE=90°,故④正确,综上所述,正确的选项①③④,故选C.
13. D 【解析】①∵∠1=∠2,∴AB∥CD,不符合题意;②∵∠3=∠4,∴BC∥AD,符合题意;③∵AB∥CD,∴∠B+∠BCD=180°,∵∠ADC=∠B,∴∠ADC+∠BCD=180°,由同旁内角互补,两直线平行可得BC∥AD,故符合题意;④∵AB∥CE,∴∠B+∠BCD=180°,∵∠BCD=∠BAD,∴∠B+∠BAD=180°,由同旁内角互补,两直线平行可得BC∥AD,故符合题意;故能推出BC∥AD的条件为②③④.故选D.
14. 真命题 【解析】“如果a3=b3,那么a=b”是真命题.
15. 对应角相等的三角形是全等三角形 【解析】命题“全等三角形对应角相等”的题设是“两个三角形是
全等三角形”,结论是“它们的对应角相等”,故其逆命题是对应角相等的三角形是全等三角形.
16. 两个角分别是某两个相等角的补角 这两个角相等 【解析】等角的补角相等的条件是两个角分别是某两个相等角的补角,结论为这两个角相等.
17. 45° 【解析】如图,∵AB∥CD,∴∠1=∠C=70°,∴∠E=∠1﹣∠A=70°﹣25°=45°.
18. 40° 【解析】∵CD∥EF,∠C=20°,∴∠CFE=∠C=20°.又∵CF平分∠AFE,∴∠AFE=2∠CFE=40°.∵AB∥EF,∴∠A=∠AFE=40°.
19. 66° 【解析】∵AB∥CD,∴∠CMF=∠1=57°,∵MF平分∠CME,∴∠CME=2∠CMF=114°.又∵∠CME+∠EMD=180°,∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
20. 72° 【解析】∵一个角的false等于另一个角的false,∴这两个角不相等,设其中一个角的度数为x°,另一个角的度数为falsex°÷false=falsex°,∵两个角的两边两两互相平行,∴x+falsex=180,解得x=72,即较小角的度数是72°.
21. 证明:∵AD⊥BC于点D,EC⊥BC于点C,∴AD∥EC,∴∠BAD=∠E,∠DAC=∠ACE,∵∠ACE=∠E,∴∠BAD=∠DAC,即AD平分∠BAC.
22. 解:∵AB∥CD,∠B=62°,∴∠BED=∠B=62°,∵EG平分∠BED,∴∠DEG=false∠BED=31°,∵EG⊥EF,∴∠FEG=90°,∴∠DEG+∠CEF=90°,∴∠CEF=90°﹣∠DEG=90°﹣31°=59°.
23. (1)∵AB∥CD,∴∠1=∠DCE=32°,∵CE平分∠ACD,∴∠ACE=∠DCE=32°;
(2)∵CF⊥CE,∴∠FCE=90°,∴∠FCH=90°﹣32°=58°,∵∠2=58°,∴∠FCH=∠2,∴CF∥AG.
24. 解:(1)DE∥BC,理由如下:∵∠1+∠4=180°,∠1+∠2=180°,∴∠2=∠4,∴AB∥EF,∴∠3=∠5,∵∠3=∠B,∴∠5=∠B,∴DE∥BC;
(2)∵DE平分∠ADC,∴∠5=∠6,∵DE∥BC,∴∠5=∠B,∵∠2=3∠B,∴∠2+∠5+∠6=3∠B+∠B+∠B=180°,∴∠B=36°,∴∠2=108°,∵∠1+∠2=180°,∴∠1=72°.
25. 解:∵EF与CD交于点H,(已知),∴∠3=∠4.(对顶角相等),∵∠3=60°,(已知),∴∠4=60°.(等量代换),∵AB∥CD,EF与AB,CD交于点G,H,(已知),∴∠4+∠FGB=180°.(两直线平行,同旁内角互补),∴∠FGB=120°.∵GM平分∠FGB,(已知),∴∠1=60°
5.3 平行线的性质1252220011303000课时训练
1.下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有一个角是60°的等腰三角形是等边三角形
C.有一组邻边相等的四边形是菱形
D.对角线相等的四边形是矩形
2.下列命题中,为假命题是( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.两组对角分别相等的四边形是平行四边形
D.对角线相等的四边形是平行四边形
3.下列命题中,其逆命题是假命题的是( )
A.两直线平行,内错角相等
B.对顶角相等
C.在一个三角形中,相等的角所对的边也相等
D.到角的两边距离相等的点在这个角的平分线上
4.下面命题:①同位角相等;②对顶角相等;③若x2=y2,则x=y;④互补的角是邻补角.其中正确命题有( )
A.1 B.2 C.3 D.4
5.如图,若AD∥BC,则下列结论正确的是( )
A.∠1=∠3 B.∠2=∠4 C.∠1=∠2 D.∠2=∠3
6.将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置,如果∠CED=46°,那么∠BAF的度数为( )
A.48° B.16° C.14° D.32°
7.如图AB∥CD,∠C=40°,∠A=60°,则∠F的度数为( )
A.10° B.20° C.30° D.40°
8.已知,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠B=64°,则∠2的度数为( )
A.20° B.26° C.30° D.35°
9.如图,直线AB∥CD,AE⊥CE,∠1=125°,则∠C等于( )
A.35° B.45° C.50° D.55°
10.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90° B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180° D.∠α+∠β+∠γ=180°
11.如图,将三角尺的直角顶点放在直尺的一边上,若∠1=60°15′,则∠2的大小为( )
A.60°15′ B.39°45′ C.29°85′ D.29°45′
12.如图,已知AD⊥BC,FG⊥BC,∠BAC=90°,DE∥AC.则结论:①FG∥AD;②DE平分ADB;③∠B=∠ADE;④∠CFG+∠BDE=90°.正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
13.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AB∥CE,且∠ADC=∠B;④AB∥CE且∠BCD=∠BAD;其中能推出BC∥AD的条件为( )
A.①② B.②④ C.②③ D.②③④
14.命题“如果a3=b3,那么a=b”是 .(填“真命题”或“假命题”)
15.命题“全等三角形的对应角相等”的逆命题是 .
16.“等角的补角相等”的条件是 ,结论是 .
17.如图,AB∥CD,∠A=25°,∠C=70°,则∠E= .
18.如图,AB∥CD∥EF,且CF平分∠AFE,若∠C=20°,则∠A的度数是 .
19.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为 .
20.两个角的两边两两互相平行,且一个角的false等于另一个角的false,则这两个角中较小角的度数为 .
21.如图,已知AD⊥BC于点D,E是延长线BA上一点,且EC⊥BC于点C,若∠ACE=∠E.求证:AD平分∠BAC.
22.如图AB∥CD,∠B=62°,EG平分∠BED,EG⊥EF,求∠CEF的度数.
23.如图,已知AB∥CD,E是直线AB上的一点,CE平分∠ACD,射线CF⊥CE,∠1=32°,
(1)求∠ACE的度数;
(2)若∠2=58°,求证:CF∥AG.
24.如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠2=3∠B,求∠1的度数.
25.如图,已知直线AB∥CD,直线EF与直线AB,CD分别交于点G,H;GM平分∠FGB,∠3=60°.求∠1的度数.
答案
1. B 【解析】选项A,一组对边平行,另一组对边相等的四边形不一定是平行四边形,原命题是假命题;选项B,有一个角是60°的等腰三角形是等边三角形,是真命题;选项C,有一组邻边相等的平行四边形是菱形,原命题是假命题;选项D,对角线相等的平行四边形是矩形.原命题是假命题. 故选B.
2. D 【解析】两组对边分别平行的四边形是平行四边形,是真命题,故选项A不符合题意;两组对边分别相等的四边形是平行四边形,是真命题,故选项B不符合题意;两组对角分别相等的四边形是平行四边形,是真命题,故选项C不符合题意;对角线互相平分的四边形是平行四边形,原命题是假命题,故选项D符合题意. 故选D.
3. B 【解析】两直线平行,内错角相等的逆命题是内错角相等,两直线平行,逆命题是真命题,故选项A不符合题意;对顶角相等的逆命题是相等的两个角是对顶角,逆命题是假命题,故选项B符合题意;在一
个三角形中,相等的角所对的边也相等的逆命题是在一个三角形中,相等的边所对的角也相等,逆命题是真命题,故选项C不符合题意;到角的两边距离相等的点在这个角的平分线上的逆命题是角的平分线上的点到角的两边距离相等,逆命题是真命题,故选项D不符合题意. 故选B.
4. A 【解析】①两直线平行,同位角相等,原命题是假命题;②对顶角相等,是真命题;③若x2=y2,则x=y或x=﹣y,原命题是假命题;④互补的角不一定是邻补角,原命题是假命题.故选A.
5. A 【解析】∵AD∥BC,∴∠3=∠1,故选A.
6. C 【解析】∵DE∥AF,∴∠CED=∠EAF=46°,∵∠BAC=90°﹣30°=60°,∴∠BAF=∠BAC﹣∠EAF=60°﹣46°=14°,故选C.
7. B 【解析】∵AB∥CD,∴∠A=∠FED=60°,∵∠FED=∠C+∠F,∴∠F=∠FED﹣∠C=60°﹣40°=20°,故选B.
8. B 【解析】∵∠1+∠B=64°,∴∠3=∠1+∠B=64°,∵a∥b,∴∠3+∠ACD+∠2=180°,∴∠2=180°﹣∠ACD﹣∠3=180°﹣90°﹣64°=26°,故选B.
9. A 【解析】过点E作EF∥AB,则EF∥CD,如图所示.∵EF∥AB,∴∠BAE=∠AEF.∵EF∥CD,∴∠C=∠CEF.∵AE⊥CE,∴∠AEC=90°,即∠AEF+∠CEF=90°,∴∠BAE+∠C=90°.∵∠1=125°,∠1+∠BAE=180°,∴∠BAE=180°﹣125°=55°,∴∠C=90°﹣55°=35°.故选A.
10. B 【解析】∵AB∥EF,∴∠α=∠BOF,∵CD∥EF,∴∠γ+∠COF=180°,∵∠BOF=∠COF+∠β,∴∠γ+∠α﹣∠β=180°,故选B.
11. D 【解析】如图,由直尺两边平行,可得∠1=∠3=60°15',∴∠2=90°﹣∠3=90°﹣60°15'=29°45',故选D.
12. C 【解析】∵AD⊥BC,FG⊥BC,∴∠FGD=∠ADB=90°,∴FG∥AD,故①正确;∵DE∥AC,∠BAC=90°,∴DE⊥AB,不能证明DE为∠ADB的平分线,故②错误;∵AD⊥BC,∴∠B+∠BAD=90°,∵DE⊥AB,∴∠BAD+∠ADE=90°,∴∠B=∠ADE,故③正确;∵∠BAC=90°,DE⊥AB,∴∠CFG+∠C=90°,∠BDE+∠B=90°,∠C+∠B=90°,∴∠CFG+∠BDE=90°,故④正确,综上所述,正确的选项①③④,故选C.
13. D 【解析】①∵∠1=∠2,∴AB∥CD,不符合题意;②∵∠3=∠4,∴BC∥AD,符合题意;③∵AB∥CD,∴∠B+∠BCD=180°,∵∠ADC=∠B,∴∠ADC+∠BCD=180°,由同旁内角互补,两直线平行可得BC∥AD,故符合题意;④∵AB∥CE,∴∠B+∠BCD=180°,∵∠BCD=∠BAD,∴∠B+∠BAD=180°,由同旁内角互补,两直线平行可得BC∥AD,故符合题意;故能推出BC∥AD的条件为②③④.故选D.
14. 真命题 【解析】“如果a3=b3,那么a=b”是真命题.
15. 对应角相等的三角形是全等三角形 【解析】命题“全等三角形对应角相等”的题设是“两个三角形是
全等三角形”,结论是“它们的对应角相等”,故其逆命题是对应角相等的三角形是全等三角形.
16. 两个角分别是某两个相等角的补角 这两个角相等 【解析】等角的补角相等的条件是两个角分别是某两个相等角的补角,结论为这两个角相等.
17. 45° 【解析】如图,∵AB∥CD,∴∠1=∠C=70°,∴∠E=∠1﹣∠A=70°﹣25°=45°.
18. 40° 【解析】∵CD∥EF,∠C=20°,∴∠CFE=∠C=20°.又∵CF平分∠AFE,∴∠AFE=2∠CFE=40°.∵AB∥EF,∴∠A=∠AFE=40°.
19. 66° 【解析】∵AB∥CD,∴∠CMF=∠1=57°,∵MF平分∠CME,∴∠CME=2∠CMF=114°.又∵∠CME+∠EMD=180°,∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
20. 72° 【解析】∵一个角的false等于另一个角的false,∴这两个角不相等,设其中一个角的度数为x°,另一个角的度数为falsex°÷false=falsex°,∵两个角的两边两两互相平行,∴x+falsex=180,解得x=72,即较小角的度数是72°.
21. 证明:∵AD⊥BC于点D,EC⊥BC于点C,∴AD∥EC,∴∠BAD=∠E,∠DAC=∠ACE,∵∠ACE=∠E,∴∠BAD=∠DAC,即AD平分∠BAC.
22. 解:∵AB∥CD,∠B=62°,∴∠BED=∠B=62°,∵EG平分∠BED,∴∠DEG=false∠BED=31°,∵EG⊥EF,∴∠FEG=90°,∴∠DEG+∠CEF=90°,∴∠CEF=90°﹣∠DEG=90°﹣31°=59°.
23. (1)∵AB∥CD,∴∠1=∠DCE=32°,∵CE平分∠ACD,∴∠ACE=∠DCE=32°;
(2)∵CF⊥CE,∴∠FCE=90°,∴∠FCH=90°﹣32°=58°,∵∠2=58°,∴∠FCH=∠2,∴CF∥AG.
24. 解:(1)DE∥BC,理由如下:∵∠1+∠4=180°,∠1+∠2=180°,∴∠2=∠4,∴AB∥EF,∴∠3=∠5,∵∠3=∠B,∴∠5=∠B,∴DE∥BC;
(2)∵DE平分∠ADC,∴∠5=∠6,∵DE∥BC,∴∠5=∠B,∵∠2=3∠B,∴∠2+∠5+∠6=3∠B+∠B+∠B=180°,∴∠B=36°,∴∠2=108°,∵∠1+∠2=180°,∴∠1=72°.
25. 解:∵EF与CD交于点H,(已知),∴∠3=∠4.(对顶角相等),∵∠3=60°,(已知),∴∠4=60°.(等量代换),∵AB∥CD,EF与AB,CD交于点G,H,(已知),∴∠4+∠FGB=180°.(两直线平行,同旁内角互补),∴∠FGB=120°.∵GM平分∠FGB,(已知),∴∠1=60°
