第2章 相交线与平行线单元测试题(教师版+学生版)
文档属性
| 名称 | 第2章 相交线与平行线单元测试题(教师版+学生版) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二章综合检测试卷 学生版
(满分:120分)
一、选择题(每小题3分,共30分)
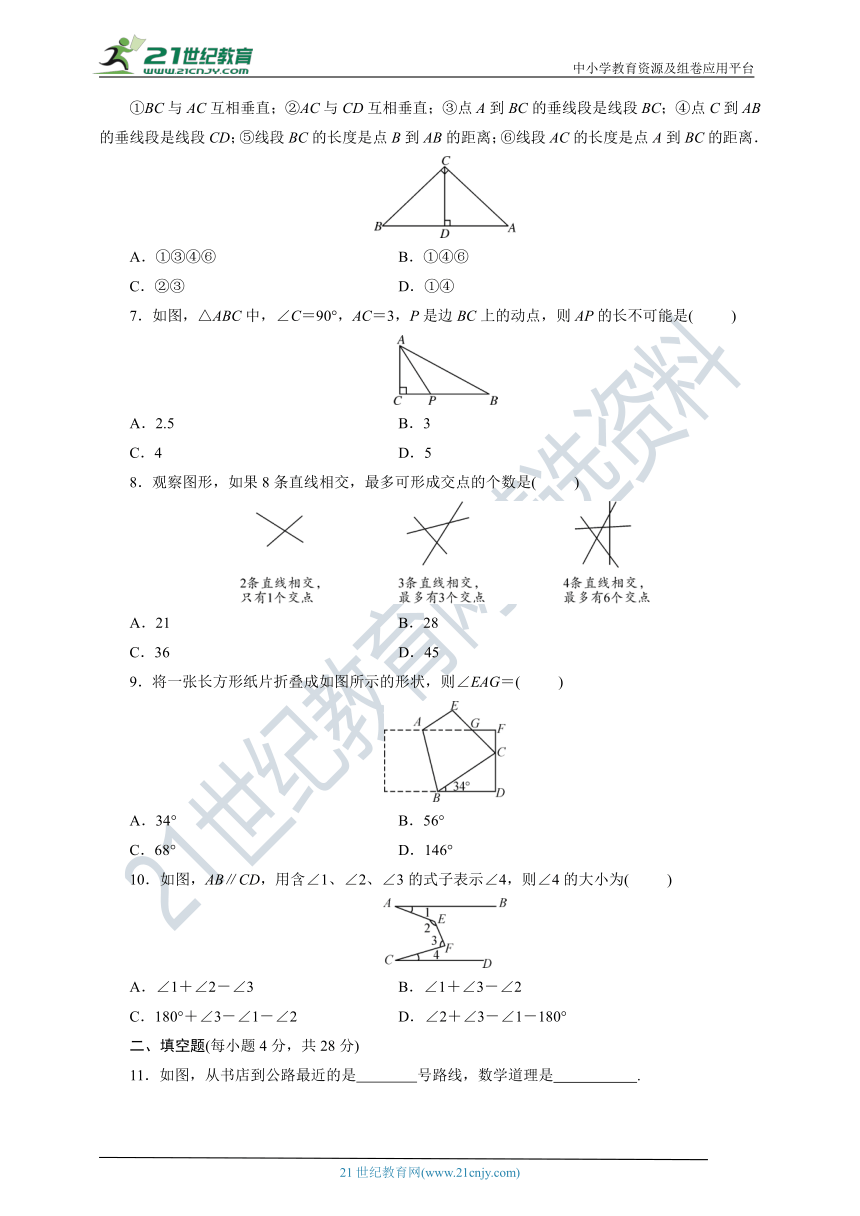
1.已知∠1与∠2是邻补角,∠2是∠3的邻补角,那么∠1与∠3的关系是( )
A.对顶角 B.相等但不是对顶角
C.邻补角 D.互补但不是邻补角
2.如图,∠AED和∠BDE是( )
A.同位角 B.内错角
C.同旁内角 D.互为补角
3.如图,点C在∠AOB的OB边上,用尺规作出了CN∥OA,作图痕迹中,是( )
A.以点C为圆心,OD为半径的弧
B.以点C为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DM为半径的弧
4.如图,能判断直线AB∥CD的条件是( )
A.∠1=∠2 B.∠3=∠4
C.∠1=∠3 D.∠3+∠4=180°
5.如图,已知直线AB、CD、MN相交于点O,∠1=22°,∠2=46°,则∠3的度数是( )
A.68° B.112°
C.44° D.68°
6.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中正确的是( )
①BC与AC互相垂直;②AC与CD互相垂直;③点A到BC的垂线段是线段BC;④点C到AB的垂线段是线段CD;⑤线段BC的长度是点B到AB的距离;⑥线段AC的长度是点A到BC的距离.
A.①③④⑥ B.①④⑥
C.②③ D.①④
7.如图,△ABC中,∠C=90°,AC=3,P是边BC上的动点,则AP的长不可能是( )
A.2.5 B.3
C.4 D.5
8.观察图形,如果8条直线相交,最多可形成交点的个数是( )
A.21 B.28
C.36 D.45
9.将一张长方形纸片折叠成如图所示的形状,则∠EAG=( )
A.34° B.56°
C.68° D.146°
10.如图,AB∥CD,用含∠1、∠2、∠3的式子表示∠4,则∠4的大小为( )
A.∠1+∠2-∠3 B.∠1+∠3-∠2
C.180°+∠3-∠1-∠2 D.∠2+∠3-∠1-180°
二、填空题(每小题4分,共28分)
11.如图,从书店到公路最近的是 号路线,数学道理是 .
12.如图,将一副三角板按不同位置摆放,其中∠α与∠β互余的是 ,∠α与∠β互补的是 ,∠α与∠β相等的是 .
13.下列说法正确的是 .(填序号)
①过直线外一点有且只有一条直线与已知直线平行;
②如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
③在同一平面内,若a∥c,b⊥a,则b⊥c.
14.一个角的补角比它的余角的2倍多8°,这个角的度数是 .
15.在同一平面内有2020条直线a1、a2、…、a2020,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,那么a1与a2020的位置关系是 .
16.如图,CD⊥AB于点D,EF⊥AB于点F,∠DGC=84°,∠BCG=96°,则∠1+∠2= .
17.从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,如入射光线OA的反射光线为AB,∠OAB=75°.在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且∠ODE=22°,则∠AOD的度数是 .
三、解答题(一)(每小题6分,共18分)
18.如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD∶∠BOE=4∶1,求∠EOF的度数.
19.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
20.如图,是我们生活中经常接触的小刀,由刀片和刀柄组成,在刀柄ABCD中,∠A和∠B都是直角,在刀片EFGH中,EF∥GH.转动刀片时会形成∠1、∠2,试判断∠1与∠2的度数和是一个定值吗?若是,请求出∠1与∠2的度数和;若不是,请说明理由.
四、解答题(二)(每小题8分,共24分)
21.如图,点C、E均在直线AB上,∠BCD=45°.
(1)在图中作∠FEB,使∠BEF=∠DCB;(保留作图痕迹,不写作法)
(2)试判断直线EF与直线CD的位置关系.
备用图
22.如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:FE∥OC;
(2)若∠BOC比∠DFE大20°,求∠OFE的度数.
23.如图,直线EF、CD相交于点O,OA⊥OB,且OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数.(用含α的代数式表示)
五、解答题(三)(每小题10分,共20分)
24.如图,已知直线l1∥l2,直线l3和直线l1、l2分别交于点C和D,在CD之间有一点P.
(1)点P在CD之间运动时,试探索∠PAC、∠APB、∠PBD之间的关系;
(2)点P在C、D两点的外侧运动时(点P与点C、D不重合),试探索∠PAC、∠APB、∠PBD之间的关系.
25.(1)如图1,AB∥CD,求∠A+∠E+∠C的度数;
(2)如图2,AB∥CD,求∠A+∠E+∠F+∠C的度数;
(3)如图3,AB∥CD,求∠A+∠E+∠F+∠G+∠C的度数;
(4)以此类推,图n中,求∠A+∠E+∠F+…+∠C的度数.
第二章综合检测试卷 教师版
(满分:120分)
一、选择题(每小题3分,共30分)
1.已知∠1与∠2是邻补角,∠2是∠3的邻补角,那么∠1与∠3的关系是( A )
A.对顶角 B.相等但不是对顶角
C.邻补角 D.互补但不是邻补角
2.如图,∠AED和∠BDE是( B )
A.同位角 B.内错角
C.同旁内角 D.互为补角
3.如图,点C在∠AOB的OB边上,用尺规作出了CN∥OA,作图痕迹中,是( D )
A.以点C为圆心,OD为半径的弧
B.以点C为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DM为半径的弧
4.如图,能判断直线AB∥CD的条件是( B )
A.∠1=∠2 B.∠3=∠4
C.∠1=∠3 D.∠3+∠4=180°
5.如图,已知直线AB、CD、MN相交于点O,∠1=22°,∠2=46°,则∠3的度数是( B )
A.68° B.112°
C.44° D.68°
6.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中正确的是( B )
①BC与AC互相垂直;②AC与CD互相垂直;③点A到BC的垂线段是线段BC;④点C到AB的垂线段是线段CD;⑤线段BC的长度是点B到AB的距离;⑥线段AC的长度是点A到BC的距离.
A.①③④⑥ B.①④⑥
C.②③ D.①④
7.如图,△ABC中,∠C=90°,AC=3,P是边BC上的动点,则AP的长不可能是( A )
A.2.5 B.3
C.4 D.5
8.观察图形,如果8条直线相交,最多可形成交点的个数是( B )
A.21 B.28
C.36 D.45
9.将一张长方形纸片折叠成如图所示的形状,则∠EAG=( A )
A.34° B.56°
C.68° D.146°
10.如图,AB∥CD,用含∠1、∠2、∠3的式子表示∠4,则∠4的大小为( D )
A.∠1+∠2-∠3 B.∠1+∠3-∠2
C.180°+∠3-∠1-∠2 D.∠2+∠3-∠1-180°
二、填空题(每小题4分,共28分)
11.如图,从书店到公路最近的是 ① 号路线,数学道理是 垂线段最短 .
12.如图,将一副三角板按不同位置摆放,其中∠α与∠β互余的是 (1) ,∠α与∠β互补的是 (4) ,∠α与∠β相等的是 (2)(3) .
13.下列说法正确的是 ①②③ .(填序号)
①过直线外一点有且只有一条直线与已知直线平行;
②如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
③在同一平面内,若a∥c,b⊥a,则b⊥c.
14.一个角的补角比它的余角的2倍多8°,这个角的度数是 8° .
15.在同一平面内有2020条直线a1、a2、…、a2020,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,那么a1与a2020的位置关系是 平行 .
16.如图,CD⊥AB于点D,EF⊥AB于点F,∠DGC=84°,∠BCG=96°,则∠1+∠2= 180° .
17.从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,如入射光线OA的反射光线为AB,∠OAB=75°.在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且∠ODE=22°,则∠AOD的度数是 53°或97° .
三、解答题(一)(每小题6分,共18分)
18.如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD∶∠BOE=4∶1,求∠EOF的度数.
解:因为OE平分∠BOD,所以∠BOD=2∠BOE.因为∠AOD+∠BOD=180°,∠AOD∶∠BOE=4∶1,所以∠AOD=4∠BOE,所以4∠BOE+2∠BOE=180°,所以∠BOE=30°.所以∠DOE=30°.因为∠DOE+∠COE=180°,所以∠COE=150°.因为OF平分∠COE,所以∠EOF=∠COE=75°.
19.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
解:OA∥BC,OB∥AC.理由如下:因为∠1=50°,∠2=50°,所以∠1=∠2,所以OB∥AC.因为∠2=50°,∠3=130°,所以∠2+∠3=180°,所以OA∥BC.
20.如图,是我们生活中经常接触的小刀,由刀片和刀柄组成,在刀柄ABCD中,∠A和∠B都是直角,在刀片EFGH中,EF∥GH.转动刀片时会形成∠1、∠2,试判断∠1与∠2的度数和是一个定值吗?若是,请求出∠1与∠2的度数和;若不是,请说明理由.
解:∠1与∠2的度数和是一个定值.过点B作BP∥EF,则∠1=∠ABP.因为EF∥GH,所以BP∥GH,所以∠2=∠PBC.因为∠ABP+∠PBC=90°,所以∠1+∠2=90°.
四、解答题(二)(每小题8分,共24分)
21.如图,点C、E均在直线AB上,∠BCD=45°.
(1)在图中作∠FEB,使∠BEF=∠DCB;(保留作图痕迹,不写作法)
(2)试判断直线EF与直线CD的位置关系.
备用图
解:(1)如图所示,∠BEF即为所求.
(2)当射线EF与射线CD在直线AB的同侧时,由∠BEF=∠BCD知,EF∥CD;当射线EF与射线CD在直线AB的两侧时,延长DC交EF于点G.因为∠BEF=∠BCD=∠ECG=45°,所以∠EGC=90°,所以EF⊥CD.
22.如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:FE∥OC;
(2)若∠BOC比∠DFE大20°,求∠OFE的度数.
(1)证明:因为AB∥DC,所以∠C=∠A.因为∠1=∠A,所以∠1=∠C,所以FE∥OC.
(2)解:因为FE∥OC,所以∠FOC+∠OFE=180°.因为∠FOC+∠BOC=180°,∠DFE+∠OFE=180°,所以∠BOC+∠DFE=180°.因为∠BOC-∠DFE=20°,所以∠DFE=80°,所以∠OFE=100°.
23.如图,直线EF、CD相交于点O,OA⊥OB,且OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数.(用含α的代数式表示)
解:(1)因为∠AOE+∠AOF=180°,∠AOE=40°,所以∠AOF=140°.又因为OC平分∠AOF,所以∠FOC=∠AOF=70°,所以∠EOD=∠FOC=70°.因为OA⊥OB,所以∠AOB=90°,∠BOE=∠AOB-∠AOE=50°,所以∠BOD=∠EOD-∠BOE=20°.
(2)因为∠AOE+∠AOF=180°,∠AOE=α,所以∠AOF=180°-α.又因为OC平分∠AOF,所以∠FOC=∠AOF=90°-α,所以∠EOD=∠FOC=90°-α.因为OA⊥OB,所以∠AOB=90°,∠BOE=∠AOB-∠AOE=90°-α,所以∠BOD=∠EOD-∠BOE=α.
五、解答题(三)(每小题10分,共20分)
24.如图,已知直线l1∥l2,直线l3和直线l1、l2分别交于点C和D,在CD之间有一点P.
(1)点P在CD之间运动时,试探索∠PAC、∠APB、∠PBD之间的关系;
(2)点P在C、D两点的外侧运动时(点P与点C、D不重合),试探索∠PAC、∠APB、∠PBD之间的关系.
解:(1)当点P在CD之间运动时,∠APB=∠PAC+∠PBD.理由:如图1,过点P作PE∥l1.因为l1∥l2,所以PE∥l2∥l1,所以∠PAC=∠1,∠PBD=∠2,所以∠APB=∠1+∠2=∠PAC+∠PBD. (2)当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.理由:如图2,因为l1∥l2,所以∠PEC=∠PBD.因为∠PEC=∠PAC+∠APB,所以∠PBD=∠PAC+∠APB.当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.理由:如图3,因为l1∥l2,所以∠PED=∠PAC.因为∠PED=∠PBD+∠APB,所以∠PAC=∠PBD+∠APB.
25.(1)如图1,AB∥CD,求∠A+∠E+∠C的度数;
(2)如图2,AB∥CD,求∠A+∠E+∠F+∠C的度数;
(3)如图3,AB∥CD,求∠A+∠E+∠F+∠G+∠C的度数;
(4)以此类推,图n中,求∠A+∠E+∠F+…+∠C的度数.
解:(1)如图1,过点E作EF∥AB.因为AB∥CD,EF∥AB,所以CD∥EF,所以∠A+∠AEF=180°,∠C+∠CEF=180°,所以∠A+∠AEC+∠C=360°.
(2)如图2,过点E作EG∥AB,过点F作FH∥AB,所以EG∥FH,∠A+∠AEG=180°,∠GEF+∠EFH=180°.因为AB∥CD,FH∥AB,所以FH∥CD,所以∠HFC+∠C=180°,所以∠A+∠AEF+∠EFC+∠C=540°.
(3)如图3,过点E作EH∥AB,过点F作FI∥AB,过点G作GJ∥AB,所以EH∥FI∥GJ,所以∠A+∠AEH=180°,∠HEF+∠EFI=180°,∠IFG+∠FGJ=180°.因为AB∥CD,GJ∥AB,所以GJ∥CD,所以∠JGC+∠C=180°,所以∠A+∠AEF+∠EFG+∠FGC+∠C=720°.
(4)由(1)(2)(3)可以看出,AB、CD之间每增加一个角,相应的角的和增加180°,当增加n个角时,度数和增加(180n)°,所以∠A+∠E+∠F+…+∠C=180°+(180n)°=(n+1)·180°.
_21?????????è?????(www.21cnjy.com)_
第二章综合检测试卷 学生版
(满分:120分)
一、选择题(每小题3分,共30分)
1.已知∠1与∠2是邻补角,∠2是∠3的邻补角,那么∠1与∠3的关系是( )
A.对顶角 B.相等但不是对顶角
C.邻补角 D.互补但不是邻补角
2.如图,∠AED和∠BDE是( )
A.同位角 B.内错角
C.同旁内角 D.互为补角
3.如图,点C在∠AOB的OB边上,用尺规作出了CN∥OA,作图痕迹中,是( )
A.以点C为圆心,OD为半径的弧
B.以点C为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DM为半径的弧
4.如图,能判断直线AB∥CD的条件是( )
A.∠1=∠2 B.∠3=∠4
C.∠1=∠3 D.∠3+∠4=180°
5.如图,已知直线AB、CD、MN相交于点O,∠1=22°,∠2=46°,则∠3的度数是( )
A.68° B.112°
C.44° D.68°
6.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中正确的是( )
①BC与AC互相垂直;②AC与CD互相垂直;③点A到BC的垂线段是线段BC;④点C到AB的垂线段是线段CD;⑤线段BC的长度是点B到AB的距离;⑥线段AC的长度是点A到BC的距离.
A.①③④⑥ B.①④⑥
C.②③ D.①④
7.如图,△ABC中,∠C=90°,AC=3,P是边BC上的动点,则AP的长不可能是( )
A.2.5 B.3
C.4 D.5
8.观察图形,如果8条直线相交,最多可形成交点的个数是( )
A.21 B.28
C.36 D.45
9.将一张长方形纸片折叠成如图所示的形状,则∠EAG=( )
A.34° B.56°
C.68° D.146°
10.如图,AB∥CD,用含∠1、∠2、∠3的式子表示∠4,则∠4的大小为( )
A.∠1+∠2-∠3 B.∠1+∠3-∠2
C.180°+∠3-∠1-∠2 D.∠2+∠3-∠1-180°
二、填空题(每小题4分,共28分)
11.如图,从书店到公路最近的是 号路线,数学道理是 .
12.如图,将一副三角板按不同位置摆放,其中∠α与∠β互余的是 ,∠α与∠β互补的是 ,∠α与∠β相等的是 .
13.下列说法正确的是 .(填序号)
①过直线外一点有且只有一条直线与已知直线平行;
②如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
③在同一平面内,若a∥c,b⊥a,则b⊥c.
14.一个角的补角比它的余角的2倍多8°,这个角的度数是 .
15.在同一平面内有2020条直线a1、a2、…、a2020,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,那么a1与a2020的位置关系是 .
16.如图,CD⊥AB于点D,EF⊥AB于点F,∠DGC=84°,∠BCG=96°,则∠1+∠2= .
17.从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,如入射光线OA的反射光线为AB,∠OAB=75°.在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且∠ODE=22°,则∠AOD的度数是 .
三、解答题(一)(每小题6分,共18分)
18.如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD∶∠BOE=4∶1,求∠EOF的度数.
19.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
20.如图,是我们生活中经常接触的小刀,由刀片和刀柄组成,在刀柄ABCD中,∠A和∠B都是直角,在刀片EFGH中,EF∥GH.转动刀片时会形成∠1、∠2,试判断∠1与∠2的度数和是一个定值吗?若是,请求出∠1与∠2的度数和;若不是,请说明理由.
四、解答题(二)(每小题8分,共24分)
21.如图,点C、E均在直线AB上,∠BCD=45°.
(1)在图中作∠FEB,使∠BEF=∠DCB;(保留作图痕迹,不写作法)
(2)试判断直线EF与直线CD的位置关系.
备用图
22.如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:FE∥OC;
(2)若∠BOC比∠DFE大20°,求∠OFE的度数.
23.如图,直线EF、CD相交于点O,OA⊥OB,且OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数.(用含α的代数式表示)
五、解答题(三)(每小题10分,共20分)
24.如图,已知直线l1∥l2,直线l3和直线l1、l2分别交于点C和D,在CD之间有一点P.
(1)点P在CD之间运动时,试探索∠PAC、∠APB、∠PBD之间的关系;
(2)点P在C、D两点的外侧运动时(点P与点C、D不重合),试探索∠PAC、∠APB、∠PBD之间的关系.
25.(1)如图1,AB∥CD,求∠A+∠E+∠C的度数;
(2)如图2,AB∥CD,求∠A+∠E+∠F+∠C的度数;
(3)如图3,AB∥CD,求∠A+∠E+∠F+∠G+∠C的度数;
(4)以此类推,图n中,求∠A+∠E+∠F+…+∠C的度数.
第二章综合检测试卷 教师版
(满分:120分)
一、选择题(每小题3分,共30分)
1.已知∠1与∠2是邻补角,∠2是∠3的邻补角,那么∠1与∠3的关系是( A )
A.对顶角 B.相等但不是对顶角
C.邻补角 D.互补但不是邻补角
2.如图,∠AED和∠BDE是( B )
A.同位角 B.内错角
C.同旁内角 D.互为补角
3.如图,点C在∠AOB的OB边上,用尺规作出了CN∥OA,作图痕迹中,是( D )
A.以点C为圆心,OD为半径的弧
B.以点C为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DM为半径的弧
4.如图,能判断直线AB∥CD的条件是( B )
A.∠1=∠2 B.∠3=∠4
C.∠1=∠3 D.∠3+∠4=180°
5.如图,已知直线AB、CD、MN相交于点O,∠1=22°,∠2=46°,则∠3的度数是( B )
A.68° B.112°
C.44° D.68°
6.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中正确的是( B )
①BC与AC互相垂直;②AC与CD互相垂直;③点A到BC的垂线段是线段BC;④点C到AB的垂线段是线段CD;⑤线段BC的长度是点B到AB的距离;⑥线段AC的长度是点A到BC的距离.
A.①③④⑥ B.①④⑥
C.②③ D.①④
7.如图,△ABC中,∠C=90°,AC=3,P是边BC上的动点,则AP的长不可能是( A )
A.2.5 B.3
C.4 D.5
8.观察图形,如果8条直线相交,最多可形成交点的个数是( B )
A.21 B.28
C.36 D.45
9.将一张长方形纸片折叠成如图所示的形状,则∠EAG=( A )
A.34° B.56°
C.68° D.146°
10.如图,AB∥CD,用含∠1、∠2、∠3的式子表示∠4,则∠4的大小为( D )
A.∠1+∠2-∠3 B.∠1+∠3-∠2
C.180°+∠3-∠1-∠2 D.∠2+∠3-∠1-180°
二、填空题(每小题4分,共28分)
11.如图,从书店到公路最近的是 ① 号路线,数学道理是 垂线段最短 .
12.如图,将一副三角板按不同位置摆放,其中∠α与∠β互余的是 (1) ,∠α与∠β互补的是 (4) ,∠α与∠β相等的是 (2)(3) .
13.下列说法正确的是 ①②③ .(填序号)
①过直线外一点有且只有一条直线与已知直线平行;
②如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
③在同一平面内,若a∥c,b⊥a,则b⊥c.
14.一个角的补角比它的余角的2倍多8°,这个角的度数是 8° .
15.在同一平面内有2020条直线a1、a2、…、a2020,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,那么a1与a2020的位置关系是 平行 .
16.如图,CD⊥AB于点D,EF⊥AB于点F,∠DGC=84°,∠BCG=96°,则∠1+∠2= 180° .
17.从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,如入射光线OA的反射光线为AB,∠OAB=75°.在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且∠ODE=22°,则∠AOD的度数是 53°或97° .
三、解答题(一)(每小题6分,共18分)
18.如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD∶∠BOE=4∶1,求∠EOF的度数.
解:因为OE平分∠BOD,所以∠BOD=2∠BOE.因为∠AOD+∠BOD=180°,∠AOD∶∠BOE=4∶1,所以∠AOD=4∠BOE,所以4∠BOE+2∠BOE=180°,所以∠BOE=30°.所以∠DOE=30°.因为∠DOE+∠COE=180°,所以∠COE=150°.因为OF平分∠COE,所以∠EOF=∠COE=75°.
19.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
解:OA∥BC,OB∥AC.理由如下:因为∠1=50°,∠2=50°,所以∠1=∠2,所以OB∥AC.因为∠2=50°,∠3=130°,所以∠2+∠3=180°,所以OA∥BC.
20.如图,是我们生活中经常接触的小刀,由刀片和刀柄组成,在刀柄ABCD中,∠A和∠B都是直角,在刀片EFGH中,EF∥GH.转动刀片时会形成∠1、∠2,试判断∠1与∠2的度数和是一个定值吗?若是,请求出∠1与∠2的度数和;若不是,请说明理由.
解:∠1与∠2的度数和是一个定值.过点B作BP∥EF,则∠1=∠ABP.因为EF∥GH,所以BP∥GH,所以∠2=∠PBC.因为∠ABP+∠PBC=90°,所以∠1+∠2=90°.
四、解答题(二)(每小题8分,共24分)
21.如图,点C、E均在直线AB上,∠BCD=45°.
(1)在图中作∠FEB,使∠BEF=∠DCB;(保留作图痕迹,不写作法)
(2)试判断直线EF与直线CD的位置关系.
备用图
解:(1)如图所示,∠BEF即为所求.
(2)当射线EF与射线CD在直线AB的同侧时,由∠BEF=∠BCD知,EF∥CD;当射线EF与射线CD在直线AB的两侧时,延长DC交EF于点G.因为∠BEF=∠BCD=∠ECG=45°,所以∠EGC=90°,所以EF⊥CD.
22.如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:FE∥OC;
(2)若∠BOC比∠DFE大20°,求∠OFE的度数.
(1)证明:因为AB∥DC,所以∠C=∠A.因为∠1=∠A,所以∠1=∠C,所以FE∥OC.
(2)解:因为FE∥OC,所以∠FOC+∠OFE=180°.因为∠FOC+∠BOC=180°,∠DFE+∠OFE=180°,所以∠BOC+∠DFE=180°.因为∠BOC-∠DFE=20°,所以∠DFE=80°,所以∠OFE=100°.
23.如图,直线EF、CD相交于点O,OA⊥OB,且OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数.(用含α的代数式表示)
解:(1)因为∠AOE+∠AOF=180°,∠AOE=40°,所以∠AOF=140°.又因为OC平分∠AOF,所以∠FOC=∠AOF=70°,所以∠EOD=∠FOC=70°.因为OA⊥OB,所以∠AOB=90°,∠BOE=∠AOB-∠AOE=50°,所以∠BOD=∠EOD-∠BOE=20°.
(2)因为∠AOE+∠AOF=180°,∠AOE=α,所以∠AOF=180°-α.又因为OC平分∠AOF,所以∠FOC=∠AOF=90°-α,所以∠EOD=∠FOC=90°-α.因为OA⊥OB,所以∠AOB=90°,∠BOE=∠AOB-∠AOE=90°-α,所以∠BOD=∠EOD-∠BOE=α.
五、解答题(三)(每小题10分,共20分)
24.如图,已知直线l1∥l2,直线l3和直线l1、l2分别交于点C和D,在CD之间有一点P.
(1)点P在CD之间运动时,试探索∠PAC、∠APB、∠PBD之间的关系;
(2)点P在C、D两点的外侧运动时(点P与点C、D不重合),试探索∠PAC、∠APB、∠PBD之间的关系.
解:(1)当点P在CD之间运动时,∠APB=∠PAC+∠PBD.理由:如图1,过点P作PE∥l1.因为l1∥l2,所以PE∥l2∥l1,所以∠PAC=∠1,∠PBD=∠2,所以∠APB=∠1+∠2=∠PAC+∠PBD. (2)当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.理由:如图2,因为l1∥l2,所以∠PEC=∠PBD.因为∠PEC=∠PAC+∠APB,所以∠PBD=∠PAC+∠APB.当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.理由:如图3,因为l1∥l2,所以∠PED=∠PAC.因为∠PED=∠PBD+∠APB,所以∠PAC=∠PBD+∠APB.
25.(1)如图1,AB∥CD,求∠A+∠E+∠C的度数;
(2)如图2,AB∥CD,求∠A+∠E+∠F+∠C的度数;
(3)如图3,AB∥CD,求∠A+∠E+∠F+∠G+∠C的度数;
(4)以此类推,图n中,求∠A+∠E+∠F+…+∠C的度数.
解:(1)如图1,过点E作EF∥AB.因为AB∥CD,EF∥AB,所以CD∥EF,所以∠A+∠AEF=180°,∠C+∠CEF=180°,所以∠A+∠AEC+∠C=360°.
(2)如图2,过点E作EG∥AB,过点F作FH∥AB,所以EG∥FH,∠A+∠AEG=180°,∠GEF+∠EFH=180°.因为AB∥CD,FH∥AB,所以FH∥CD,所以∠HFC+∠C=180°,所以∠A+∠AEF+∠EFC+∠C=540°.
(3)如图3,过点E作EH∥AB,过点F作FI∥AB,过点G作GJ∥AB,所以EH∥FI∥GJ,所以∠A+∠AEH=180°,∠HEF+∠EFI=180°,∠IFG+∠FGJ=180°.因为AB∥CD,GJ∥AB,所以GJ∥CD,所以∠JGC+∠C=180°,所以∠A+∠AEF+∠EFG+∠FGC+∠C=720°.
(4)由(1)(2)(3)可以看出,AB、CD之间每增加一个角,相应的角的和增加180°,当增加n个角时,度数和增加(180n)°,所以∠A+∠E+∠F+…+∠C=180°+(180n)°=(n+1)·180°.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
