思想方法篇 第2讲 数形结合思想 课件(共19张PPT)2021届高考数学三轮复习
文档属性
| 名称 | 思想方法篇 第2讲 数形结合思想 课件(共19张PPT)2021届高考数学三轮复习 |

|
|
| 格式 | pptx | ||
| 文件大小 | 784.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-21 00:00:00 | ||
图片预览






文档简介
第2讲 数形结合思想
思想概述 数形结合思想,就是根据数与形之间的对应关系,通过数与形的相互转化来解决数学问题的思想.数形结合思想的应用包括以下两个方面:(1)“以形助数”,把某些抽象的数学问题直观化、生动化,能够变抽象思维为形象思维,揭示数学问题的本质;(2)“以数定形”,把直观图形数量化,使形更加精确.
内
容
索
引
方法一
方法二
方法三
利用函数图象可直观研究函数的性质,求解与函数有关的方程、不等式问题.
方法一 利用数形结合求解函数与方程、不等式问题
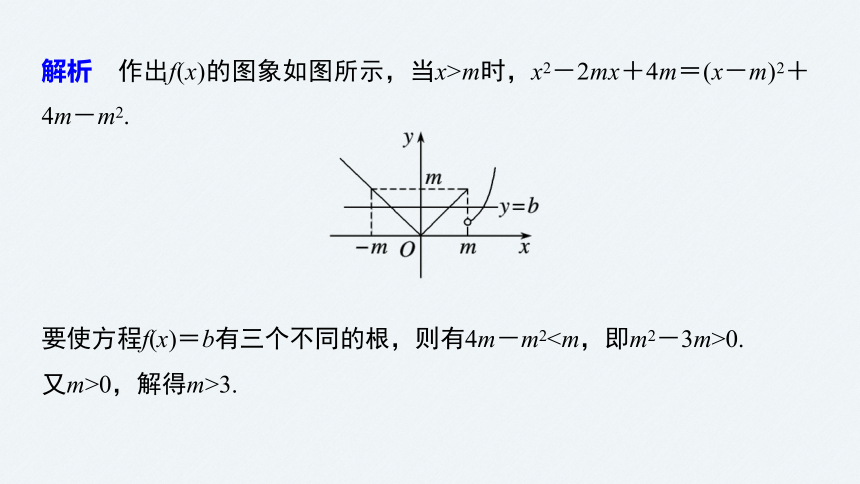
例1 已知函数f(x)= 其中m>0.若存在实数b,
使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是__________.
思路分析 方程f(x)=b有三个不同的根→函数y=f(x)的图象和直线y=b有三个交点→画函数图象
(3,+∞)
解析 作出f(x)的图象如图所示,当x>m时,x2-2mx+4m=(x-m)2+4m-m2.
要使方程f(x)=b有三个不同的根,则有4m-m20.
又m>0,解得m>3.
批注
正确作出两个函数图象是解题关键,直观是本解法的最大优势.
例2 当x∈(1,2)时,不等式(x-1)2{a|1 解析 设y=(x-1)2,y=logax,在同一坐标系中作出它们的图象,如图所示.
若0 所以底数a的取值范围为{a|1规律方法
方程解的个数问题可通过构造函数,转化为函数图象的交点个数问题;f(x) 向量、复数等数学概念具有明显的几何意义,可利用图形观察求解有关问题;灵活应用一些几何结构的代数形式,如斜率、距离公式等.
方法二 利用数学概念表达式的几何意义求解最值、范围问题
例3 已知a,b是平面内两个互相垂直的单位向量,若向量c满足(a-c)·(b-c)=0,则|c|的最大值是
√
思路分析 求|c|的最大值→考虑向量a,b,c的几何关系→通过几何意义观察|c|的最值
解析 如图,
∴O,A,C,B四点共圆.
例4 已知实数x,y满足 则x2+y2的取值范围是________.
思路分析 求x2+y2的取值范围→P(x,y)和O(0,0)距离的范围→点到直线的距离
解析 已知不等式组所表示的平面区域如图所示(阴影部分含边界),
x2+y2表示原点到可行区域内的点的距离的平方.
得A(2,3).
(x2+y2)max=|OA|2=22+32=13.
规律方法
应用几何意义法解决问题需要熟悉常见的几何结构的代数形式,主要有:①比值——可考虑直线的斜率;②二元一次式—可考虑直线的截距;③根式分式——可考虑点到直线的距离;④根式——可考虑两点间的距离.
对一些几何动态中的代数求解问题,可以结合各个变量的形成过程,找出其中的相互关系求解.
例5 已知抛物线的方程为x2=8y,点F是其焦点,点A(-2,4),在抛物线上求一点P,使△APF的周长最小,求此时点P的坐标.
思路分析 △APF的周长最小→结合抛物线定义转化|PF|=|PQ|→结合图形观察三边关系求最值
方法三 几何动态问题中的数形结合
解 因为(-2)2<8×4,所以点A(-2,4)在抛物线x2=8y的内部,如图,
设抛物线的准线为l,过点P作PQ⊥l于点Q,过点A作AB⊥l于点B,连接AQ.
则△APF的周长为|PF|+|PA|+|AF|=|PQ|+|PA|+|AF|≥|AQ|+|AF|≥|AB|+|AF|,当且仅当P,B,A三点共线时,△APF的周长取得最小值,即|AB|+|AF|.
批注
通过定义转化|PF|=|PQ|,利用三角形两边之和大于第三边,两次放缩,图形间的关系是解题关键.
规律方法
几何图形有关的最值问题,若通过代数方法计算则小题大做,计算繁杂,解题时要充分考虑几何关系,充分利用“三角形两边之和大于第三边”、“两点之间线段最短”等几何结论.
本课结束
思想概述 数形结合思想,就是根据数与形之间的对应关系,通过数与形的相互转化来解决数学问题的思想.数形结合思想的应用包括以下两个方面:(1)“以形助数”,把某些抽象的数学问题直观化、生动化,能够变抽象思维为形象思维,揭示数学问题的本质;(2)“以数定形”,把直观图形数量化,使形更加精确.
内
容
索
引
方法一
方法二
方法三
利用函数图象可直观研究函数的性质,求解与函数有关的方程、不等式问题.
方法一 利用数形结合求解函数与方程、不等式问题
例1 已知函数f(x)= 其中m>0.若存在实数b,
使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是__________.
思路分析 方程f(x)=b有三个不同的根→函数y=f(x)的图象和直线y=b有三个交点→画函数图象
(3,+∞)
解析 作出f(x)的图象如图所示,当x>m时,x2-2mx+4m=(x-m)2+4m-m2.
要使方程f(x)=b有三个不同的根,则有4m-m2
又m>0,解得m>3.
批注
正确作出两个函数图象是解题关键,直观是本解法的最大优势.
例2 当x∈(1,2)时,不等式(x-1)2
若0
方程解的个数问题可通过构造函数,转化为函数图象的交点个数问题;f(x)
方法二 利用数学概念表达式的几何意义求解最值、范围问题
例3 已知a,b是平面内两个互相垂直的单位向量,若向量c满足(a-c)·(b-c)=0,则|c|的最大值是
√
思路分析 求|c|的最大值→考虑向量a,b,c的几何关系→通过几何意义观察|c|的最值
解析 如图,
∴O,A,C,B四点共圆.
例4 已知实数x,y满足 则x2+y2的取值范围是________.
思路分析 求x2+y2的取值范围→P(x,y)和O(0,0)距离的范围→点到直线的距离
解析 已知不等式组所表示的平面区域如图所示(阴影部分含边界),
x2+y2表示原点到可行区域内的点的距离的平方.
得A(2,3).
(x2+y2)max=|OA|2=22+32=13.
规律方法
应用几何意义法解决问题需要熟悉常见的几何结构的代数形式,主要有:①比值——可考虑直线的斜率;②二元一次式—可考虑直线的截距;③根式分式——可考虑点到直线的距离;④根式——可考虑两点间的距离.
对一些几何动态中的代数求解问题,可以结合各个变量的形成过程,找出其中的相互关系求解.
例5 已知抛物线的方程为x2=8y,点F是其焦点,点A(-2,4),在抛物线上求一点P,使△APF的周长最小,求此时点P的坐标.
思路分析 △APF的周长最小→结合抛物线定义转化|PF|=|PQ|→结合图形观察三边关系求最值
方法三 几何动态问题中的数形结合
解 因为(-2)2<8×4,所以点A(-2,4)在抛物线x2=8y的内部,如图,
设抛物线的准线为l,过点P作PQ⊥l于点Q,过点A作AB⊥l于点B,连接AQ.
则△APF的周长为|PF|+|PA|+|AF|=|PQ|+|PA|+|AF|≥|AQ|+|AF|≥|AB|+|AF|,当且仅当P,B,A三点共线时,△APF的周长取得最小值,即|AB|+|AF|.
批注
通过定义转化|PF|=|PQ|,利用三角形两边之和大于第三边,两次放缩,图形间的关系是解题关键.
规律方法
几何图形有关的最值问题,若通过代数方法计算则小题大做,计算繁杂,解题时要充分考虑几何关系,充分利用“三角形两边之和大于第三边”、“两点之间线段最短”等几何结论.
本课结束
同课章节目录
