2020-2021学年北师大版八年级下册数学课件 2.2 不等式的基本性质(共15张PPT)
文档属性
| 名称 | 2020-2021学年北师大版八年级下册数学课件 2.2 不等式的基本性质(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 520.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 21:50:31 | ||
图片预览





文档简介
(共15张PPT)
2.2
不等式的基本性质
第二章
一元一次不等式与
一元一次不等式组
1.理解并掌握不等式的基本性质1,2,3;
2.掌握并能熟练应用不等式的基本性质进行不等式
的变形(重点);
3.理解不等式的基本性质与等式基本性质之间的区
别与联系
(难点).
学习目标
导入新课
复习引入
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
等式的这些性质适用于不等式吗?不等式有哪些性质呢?
等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.
讲授新课
不等式的性质
一
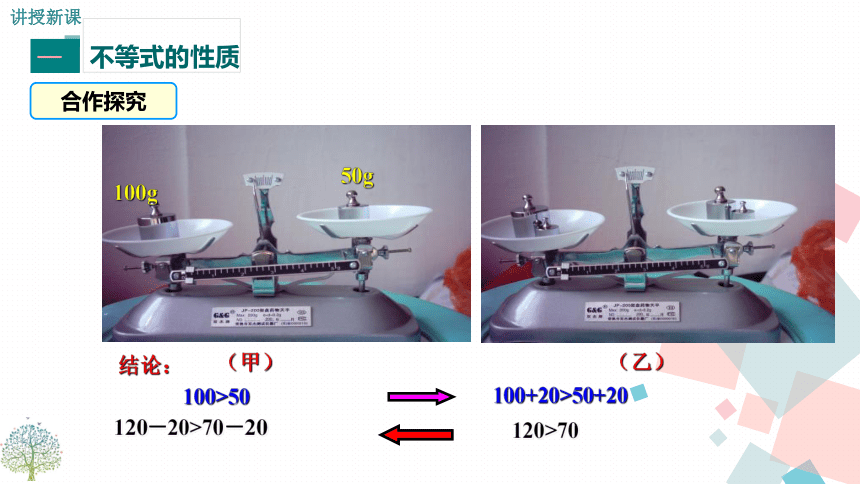
合作探究
(甲)
(乙)
100g
50g
结论:
100>50
100+20>50+20
120>70
120-20>70-20
(1)5>3,
5+2___3+2
,
5-2___3-2
;
(2)-1<3,
-1+2___3+2
,
-1-3___3-3
;
根据发现的规律填空:当不等式两边加或减同一个数(正数或负数)时,不等号的方向______.
不变
﹥
﹥
﹤
﹤
思考:用“﹥”或“﹤”填空,并总结其中的规律:
(3)
6>2,
6×5____2×5
,
6×(-5)____2×(-5)
;
(4)–2<3,
(-2)×6___3×6
,
(-2)
×(-6)___3×(-6
)
当不等式两边乘同一个正数时,不等号的方向_____;
而乘同一个负数时,不等号的方向_____;
改变
﹥
﹤
﹤
﹥
不变
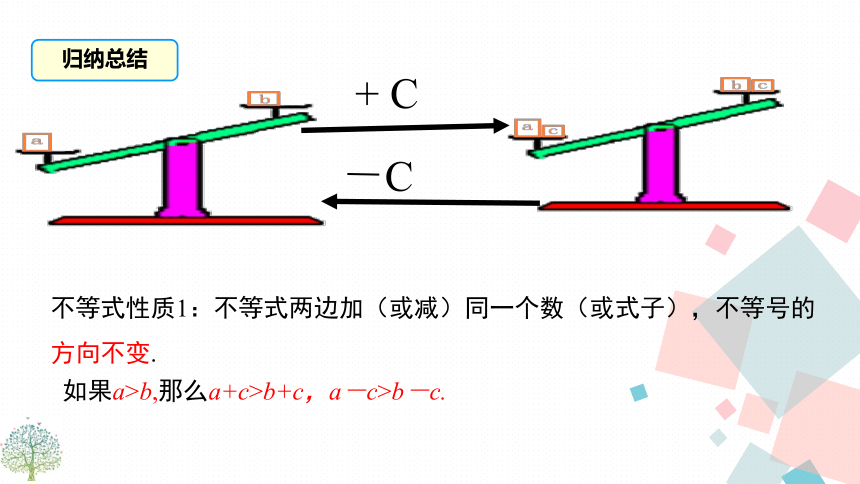
+
C
-C
不等式性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a+c>b+c,a-c>b-c.
归纳总结
如果a>b,c>0,那么ac____bc(或
)
不等式的性质2
不等式两边乘(或除以)同一个正数,不等号的方向不变.
>
如果a>b,c<0,那么ac
____bc(或
)
﹤
不等式的性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变.
1.设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1)
a
-
3____b
-
3;
(2)
a÷3____b÷3
(3)
0.1a____0.1b;
(4)
-4a____-4b
(5)
2a+3____2b+3;
(6)(m2+1)a____
(m2+1)b(m为常数)
>
>
>
>
>
<
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质3
不等式的性质1,2
不等式的性质2
练一练
2.已知a<0,用“<”“>”填空:
(1)a+2
____2;
?(2)a-1
_____-1;
(3)3a______0;
(4)
______0;
(5)a2_____0;
(6)a3______0;
(7)a-1_____0;??(8)|a|______0.
<
<
<
>
<
>
<
>
不等式的两边都乘以16,由不等式基本性质2,得
解:
不等式的两边都除以l2,由不等式基本性质2,得
因为上式是恒等式,所以
也为恒等式.
思考:上节课,我们猜想,无论绳长
l
取何值,圆的面积总大于正方形的面积,即
.你相信这个结论吗?你能用不等式的性质证明吗?
解:
(1)不等式的两边都加上5,由不等式基本
性质1,得
x
>
-1
+5,
即
x
>
4
.
例
将下列不等式化成“x>a”“x<a”的形式.
(1)x
-5
>
-1
;
(2)
-2x>
3
;
(2)不等式的两边都除以-2,由不等式基本
性质3,得
利用不等式的性质把不等式化成x>a、x<a的形式
二
(3)
x
-7
<
8,
解:
不等式的两边都加上7,由不等式基本性质1,得
x
-7+7
<
8+7,
即
x
<
15
.
(3)x
-7
<
8
;
(4)
3x
<
2x
-3
.
(4)
3x
<
2x
-3,
不等式的两边都减去2x,由不等式基本性质1,得
3x
-2x
<
2x-3-2x,
即
x
<
-3.
当堂练习
1.
已知a
<
b,用“>”或“<”填空:
(1)a
+12
b
+12
;
(2)b
-10
a
-10
.
<
>
解:x
<
2
解:x
<
6
2.
把下列不等式化为x>a或x(1)5>3+x;
(2)2x<x+6.
课堂小结
不等式的基本性质
不等式基本性质2
不等式基本性质3
→
→
如果
那么
如果
那么
应用性质对不等式简单变形
不等式的基本性质1
如果a>b,那么a+c>b+c,
a-c>b-c
→
2.2
不等式的基本性质
第二章
一元一次不等式与
一元一次不等式组
1.理解并掌握不等式的基本性质1,2,3;
2.掌握并能熟练应用不等式的基本性质进行不等式
的变形(重点);
3.理解不等式的基本性质与等式基本性质之间的区
别与联系
(难点).
学习目标
导入新课
复习引入
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
等式的这些性质适用于不等式吗?不等式有哪些性质呢?
等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.
讲授新课
不等式的性质
一
合作探究
(甲)
(乙)
100g
50g
结论:
100>50
100+20>50+20
120>70
120-20>70-20
(1)5>3,
5+2___3+2
,
5-2___3-2
;
(2)-1<3,
-1+2___3+2
,
-1-3___3-3
;
根据发现的规律填空:当不等式两边加或减同一个数(正数或负数)时,不等号的方向______.
不变
﹥
﹥
﹤
﹤
思考:用“﹥”或“﹤”填空,并总结其中的规律:
(3)
6>2,
6×5____2×5
,
6×(-5)____2×(-5)
;
(4)–2<3,
(-2)×6___3×6
,
(-2)
×(-6)___3×(-6
)
当不等式两边乘同一个正数时,不等号的方向_____;
而乘同一个负数时,不等号的方向_____;
改变
﹥
﹤
﹤
﹥
不变
+
C
-C
不等式性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a+c>b+c,a-c>b-c.
归纳总结
如果a>b,c>0,那么ac____bc(或
)
不等式的性质2
不等式两边乘(或除以)同一个正数,不等号的方向不变.
>
如果a>b,c<0,那么ac
____bc(或
)
﹤
不等式的性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变.
1.设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1)
a
-
3____b
-
3;
(2)
a÷3____b÷3
(3)
0.1a____0.1b;
(4)
-4a____-4b
(5)
2a+3____2b+3;
(6)(m2+1)a____
(m2+1)b(m为常数)
>
>
>
>
>
<
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质3
不等式的性质1,2
不等式的性质2
练一练
2.已知a<0,用“<”“>”填空:
(1)a+2
____2;
?(2)a-1
_____-1;
(3)3a______0;
(4)
______0;
(5)a2_____0;
(6)a3______0;
(7)a-1_____0;??(8)|a|______0.
<
<
<
>
<
>
<
>
不等式的两边都乘以16,由不等式基本性质2,得
解:
不等式的两边都除以l2,由不等式基本性质2,得
因为上式是恒等式,所以
也为恒等式.
思考:上节课,我们猜想,无论绳长
l
取何值,圆的面积总大于正方形的面积,即
.你相信这个结论吗?你能用不等式的性质证明吗?
解:
(1)不等式的两边都加上5,由不等式基本
性质1,得
x
>
-1
+5,
即
x
>
4
.
例
将下列不等式化成“x>a”“x<a”的形式.
(1)x
-5
>
-1
;
(2)
-2x>
3
;
(2)不等式的两边都除以-2,由不等式基本
性质3,得
利用不等式的性质把不等式化成x>a、x<a的形式
二
(3)
x
-7
<
8,
解:
不等式的两边都加上7,由不等式基本性质1,得
x
-7+7
<
8+7,
即
x
<
15
.
(3)x
-7
<
8
;
(4)
3x
<
2x
-3
.
(4)
3x
<
2x
-3,
不等式的两边都减去2x,由不等式基本性质1,得
3x
-2x
<
2x-3-2x,
即
x
<
-3.
当堂练习
1.
已知a
<
b,用“>”或“<”填空:
(1)a
+12
b
+12
;
(2)b
-10
a
-10
.
<
>
解:x
<
2
解:x
<
6
2.
把下列不等式化为x>a或x
(2)2x<x+6.
课堂小结
不等式的基本性质
不等式基本性质2
不等式基本性质3
→
→
如果
那么
如果
那么
应用性质对不等式简单变形
不等式的基本性质1
如果a>b,那么a+c>b+c,
a-c>b-c
→
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
