2020-2021学年青岛六三制小学六年级数学下册《第5章 奥运奖牌—扇形统计图》单元测试题(含解析)
文档属性
| 名称 | 2020-2021学年青岛六三制小学六年级数学下册《第5章 奥运奖牌—扇形统计图》单元测试题(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 413.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 00:00:00 | ||
图片预览

文档简介
2020-2021学年青岛六三制小学六年级数学下册《第5章
奥运奖牌—扇形统计图》单元测试题
一.选择题(共8小题)
1.如图是六(3)和六(4)两个班级男、女生人数统计图,下列说法正确的是( )
A.六(4)班的男生比六(3)班的男生少
B.六(4)班的女生比六(3)班的女生多
C.六(4)班的学生比六(3)班的学生多
D.根据现在数据,不同班级间无法比较
2.某公司有员工700人,元旦要举行活动,如图是分别参加活动的人数的百分比,规定每人只允许参加一项且每人均参加,则不下围棋的人共有( )
A.259人
B.441人
C.350人
D.490人
3.某中学七年级二班学生有32%的同学喜欢打乒乓球,有68%的同学喜欢其他球类活动,若将上述情况画成一个扇形统计图,表示喜欢乒乓球的扇形的圆心角等于( )
A.120°
B.105.2°
C.115.2°
D.115°
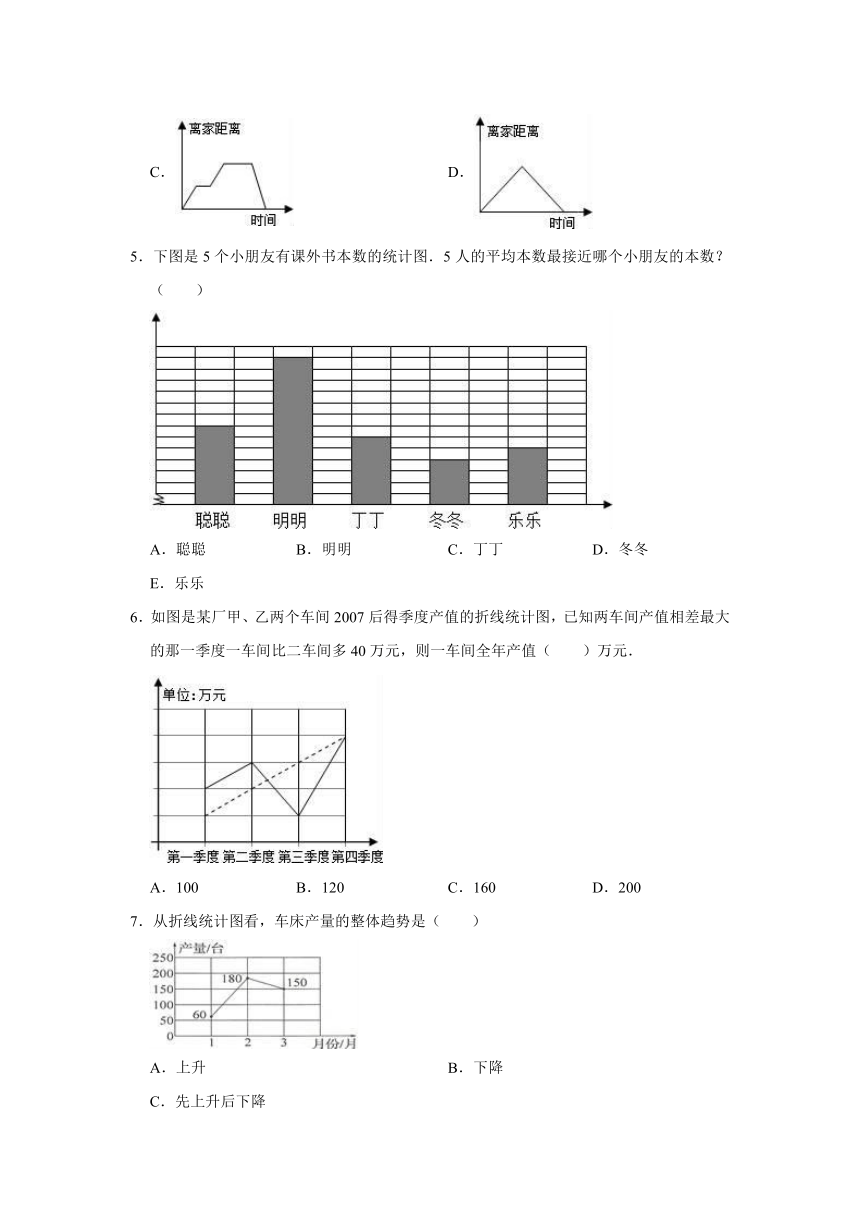
4.小红从家去图书馆借书,中途休息了几分钟,借完书后直接回家.下面正确描述小红这一过程的图象是( )
A.
B.
C.
D.
5.下图是5个小朋友有课外书本数的统计图.5人的平均本数最接近哪个小朋友的本数?( )
A.聪聪
B.明明
C.丁丁
D.冬冬
E.乐乐
6.如图是某厂甲、乙两个车间2007后得季度产值的折线统计图,已知两车间产值相差最大的那一季度一车间比二车间多40万元,则一车间全年产值( )万元.
A.100
B.120
C.160
D.200
7.从折线统计图看,车床产量的整体趋势是( )
A.上升
B.下降
C.先上升后下降
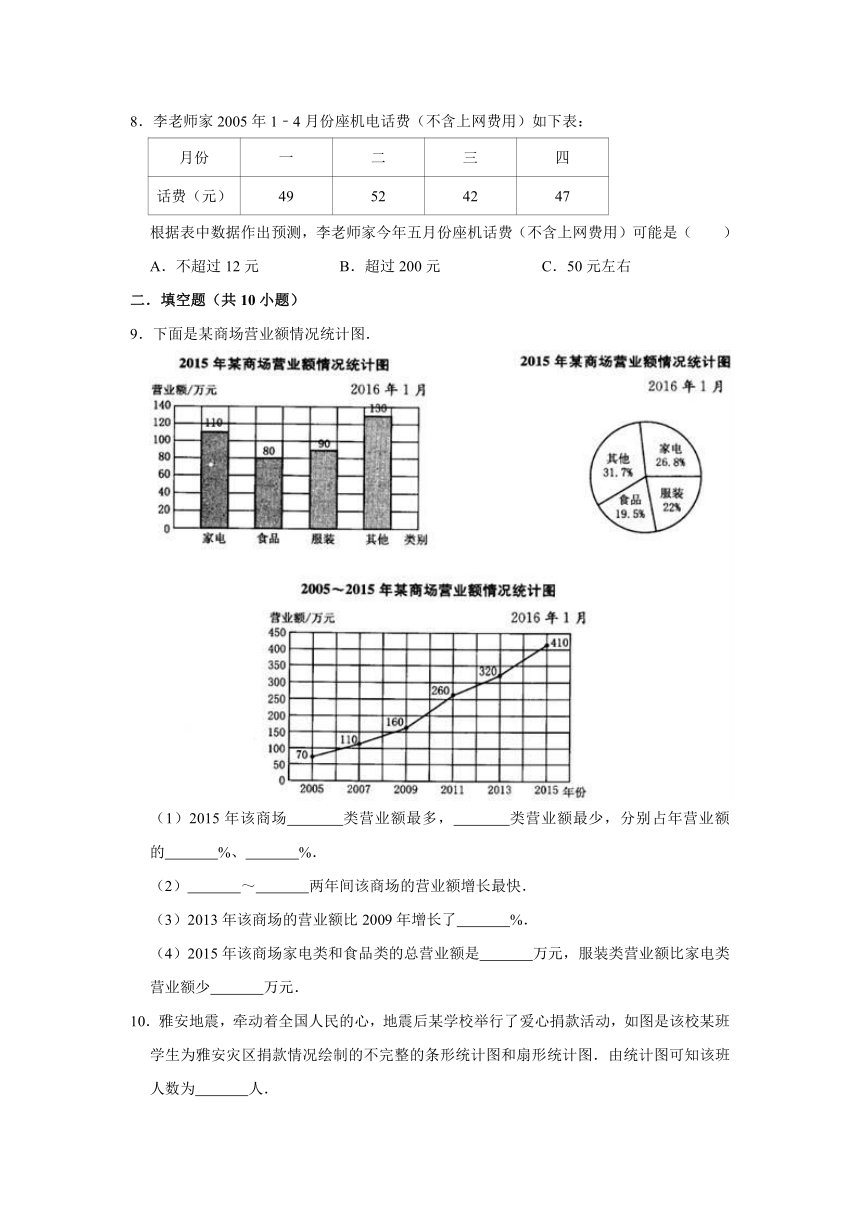
8.李老师家2005年1﹣4月份座机电话费(不含上网费用)如下表:
月份
一
二
三
四
话费(元)
49
52
42
47
根据表中数据作出预测,李老师家今年五月份座机话费(不含上网费用)可能是( )
A.不超过12元
B.超过200元
C.50元左右
二.填空题(共10小题)
9.下面是某商场营业额情况统计图.
(1)2015年该商场
类营业额最多,
类营业额最少,分别占年营业额的
%、
%.
(2)
~
两年间该商场的营业额增长最快.
(3)2013年该商场的营业额比2009年增长了
%.
(4)2015年该商场家电类和食品类的总营业额是
万元,服装类营业额比家电类营业额少
万元.
10.雅安地震,牵动着全国人民的心,地震后某学校举行了爱心捐款活动,如图是该校某班学生为雅安灾区捐款情况绘制的不完整的条形统计图和扇形统计图.由统计图可知该班人数为
人.
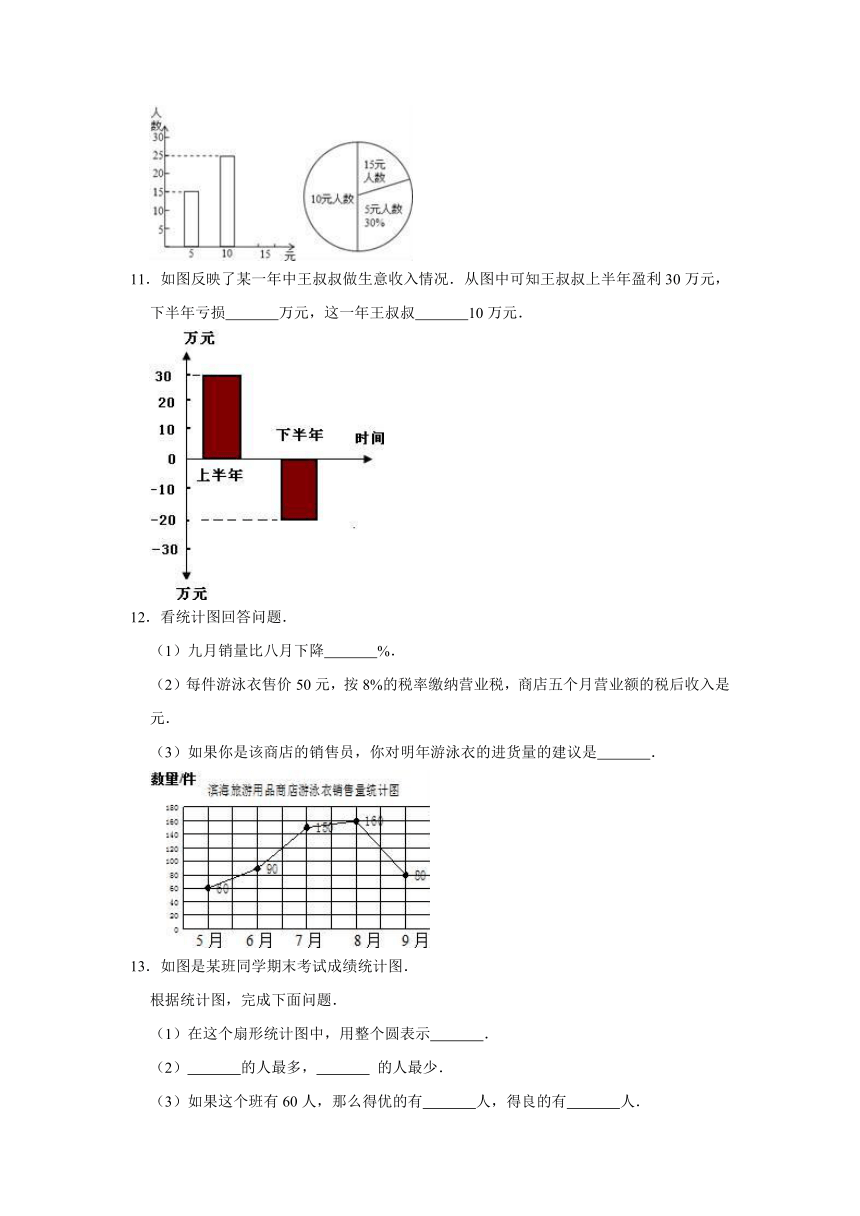
11.如图反映了某一年中王叔叔做生意收入情况.从图中可知王叔叔上半年盈利30万元,下半年亏损
万元,这一年王叔叔
10万元.
12.看统计图回答问题.
(1)九月销量比八月下降
%.
(2)每件游泳衣售价50元,按8%的税率缴纳营业税,商店五个月营业额的税后收入是
元.
(3)如果你是该商店的销售员,你对明年游泳衣的进货量的建议是
.
13.如图是某班同学期末考试成绩统计图.
根据统计图,完成下面问题.
(1)在这个扇形统计图中,用整个圆表示
.
(2)
的人最多,
的人最少.
(3)如果这个班有60人,那么得优的有
人,得良的有
人.
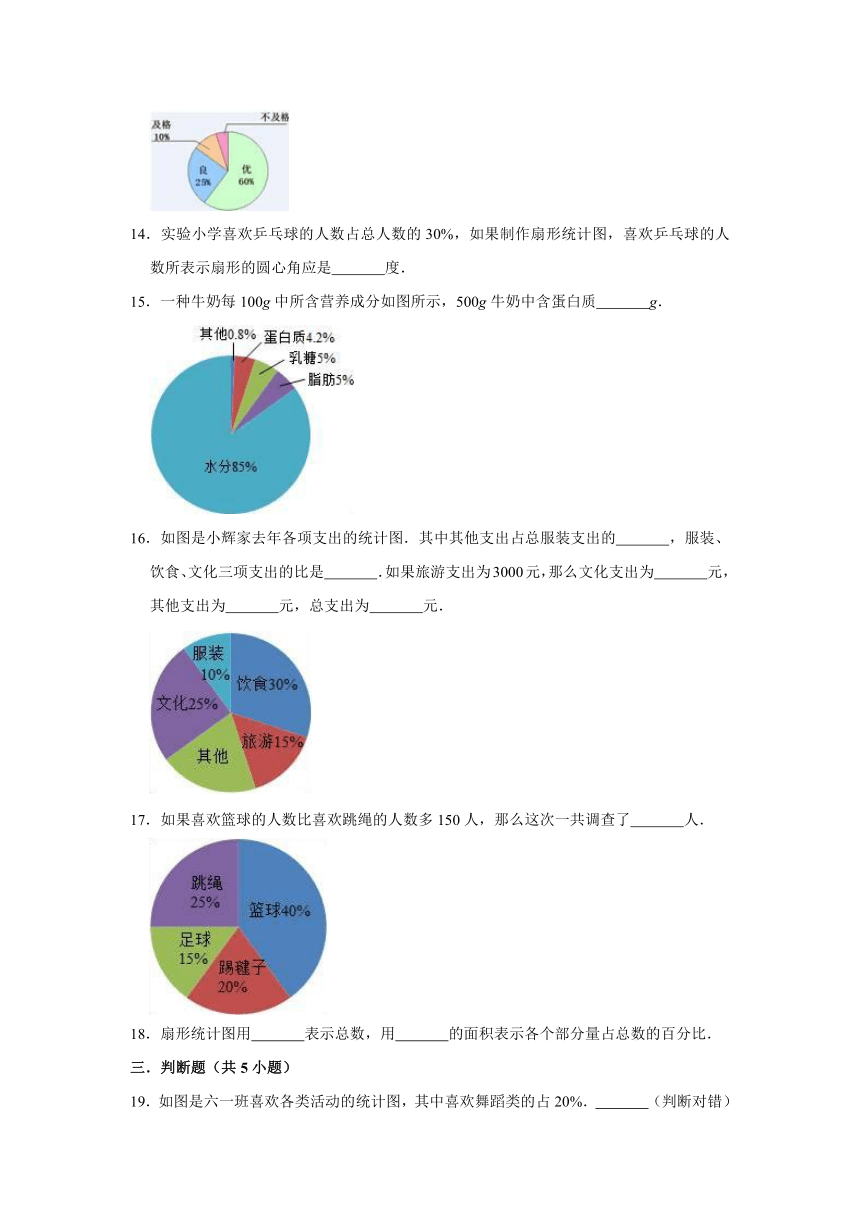
14.实验小学喜欢乒乓球的人数占总人数的30%,如果制作扇形统计图,喜欢乒乓球的人数所表示扇形的圆心角应是
度.
15.一种牛奶每100g中所含营养成分如图所示,500g牛奶中含蛋白质
g.
16.如图是小辉家去年各项支出的统计图.其中其他支出占总服装支出的
,服装、饮食、文化三项支出的比是
.如果旅游支出为3000元,那么文化支出为
元,其他支出为
元,总支出为
元.
17.如果喜欢篮球的人数比喜欢跳绳的人数多150人,那么这次一共调查了
人.
18.扇形统计图用
表示总数,用
的面积表示各个部分量占总数的百分比.
三.判断题(共5小题)
19.如图是六一班喜欢各类活动的统计图,其中喜欢舞蹈类的占20%.
(判断对错)
20.如图是某校同学参加课外兴趣小组,其中参加歌咏小组的人数最多.
(判断对错)
21.晶晶家5月份食品支出占生活总支出的30%,在制作扇形统计图时,表示食品支出的扇形的圆心角是30°.
(判断对错)
22.如图中,及格的人数比良好的人数少15%.
(判断对错)
23.扇形统计图可直观看出统计数据各部分占总体的比率.
.(判断对错)
四.应用题(共4小题)
24.如图是向阳小学六(1)班同学最喜欢体育项目情况的统计图.
①如果喜欢乒乓球的有16人,那么喜欢乒乓球与喜欢足球的人数比是多少?
②喜欢乒乓球的比喜欢篮球的人多百分之几?
25.一个8人小组想知道他们小组更喜欢音乐还是美术,于是他们用1、2、3、4、5分别表示非常不喜欢、不喜欢、一般、喜欢、非常喜欢,结果如表.
学生1
学生2
学生3
学生4
学生5
学生6
学生7
学生8
音乐
3
2
5
1
3
2
5
3
美术
5
3
4
4
5
2
4
5
你认为哪个科目更受欢迎?
26.下面两图,是根据某校六年级(1)班一次数学测试成绩数据绘制成的统计图,请结合两幅统计图提供的信息,回答下面问题.
(1)列式计算出六年级(1)班数学测试成绩优秀人数比及格人数多百分之几?
(2)列式计算出六年级(1)班有多少人参加本次数学测试?
(3)列式计算不及格人数占六年级(1)班测试总人数的百分之几?
(4)把条形统计图和扇形统计图补充或填写完整.
27.如图是实验小学六(2)班同学最喜欢的一项球类活动调查统计图。
(1)喜欢足球的占百分之几?
(2)如果六(2)班有60人,那么喜欢乒乓球的有多少人?
五.操作题(共3小题)
28.某商场2018年销售总额是1200万元.其中第一季度销售额是408万元.根据上述信息,完成如图统计图.
29.六(2)班上学期期末的体育成绩得优的有12人,得良的有16人,及格的有10人,不及格的有2人,利用如图的图形,制成扇形统计图,分别表示不同成绩人数各占全班人数的百分之几.
30.淘气把调查的六一班同学最喜欢的学科的情况制成了下面的统计图.从图中可以看出.
①一共调查了
名同学.
②喜欢数学的男生比女生多
%.
③参与调查的男生共
人.
六.解答题(共1小题)
31.如图是某校同学喜欢的球类运动统计图。
(1)观察上面的扇形统计图,回答问题。
①最受欢迎的两种球类活动是
和
,它们的百分比之和是
。
②如果你是体育委员,准备组织全班同学去观看球类比赛。为了吸引尽可能多的同学参与,你会组织观看
比赛。
(2)如果这个学校共有学生1000名,请你根据统计图提出一个数学问题并解答。
参考答案与试题解析
一.选择题(共8小题)
1.【分析】由第一个图可知:六(3)班的总人数是单位“1”男生占54%,女生占46%;
由第二个图可知:六(4)班的总人数是单位“1”,男生占52%,女占48%;由此求解;
【解答】解:两个图的单位“1”不相同,一个是六(3)班的总人数,一个是六(4)班的总人数;
而两个班的各有多少人未知,它们的百分之几是多少就无法求解,两个班之间的人数就无法比较.
故选:D.
【点评】解决本题关键是找出两个图它们的单位“1”不同,两个班的总人数未知,无法比较两个班之间的人数多少.
2.【分析】不下围棋的人数的百分比是1﹣37%,不下围棋的人共有700×(1﹣37%)人,即可得解.
【解答】解:700×(1﹣37%)
=700×63%
=441(人)
答:不下围棋的人共有441人.
故选:B.
【点评】此题主要考查的是如何观察扇形统计图并且从统计图中获取信息,然后再进行计算、解答即可.
3.【分析】一个扇形统计图的总圆心角是360°,有32%的同学喜欢打乒乓球,求表示喜欢乒乓球的扇形的圆心角等于多少用乘法,即可得解.
【解答】解:360×32%=115.2°,
答:表示喜欢乒乓球的扇形的圆心角等于115.2°;
故选:C.
【点评】扇形统计图是用整个圆表示总数(单位“1”),用圆内各个扇形的大小表示各部分量占总数量的百分之几,扇形统计图中各部分的百分比之和等于“1”.通过扇形统计图可以很清楚地表出各部分数量同总数之间的关系,而不是反应变化趋势.
4.【分析】根据所给的条件,分析出时间与离家距离之间的关系,再从选项中找出符合的答案.
【解答】解:小红的这一过程可分成以下几段:
(1)从家出发到途中休息前,这一段时间里离家的距离越来越远;
(2)途中休息,这一段时间离家的距离不变;
(3)途中休息后到图书馆,这一段时间里离家的距离越来越远;
(4)在图书馆借书,这一段时间离家的距离不变;
(5)从图书馆回家,这一段时间里离家的距离越来越近.
只有选项C符合这一变化.
故选:C.
【点评】这类题目关键是找出离家的距离随时间的变化是怎么变化的,分好段求解.
5.【分析】通过观察可知:这5个小朋友的课外书的数量是7+13+6+4+5=35本,每个小朋友平均有:35÷5=7本,由图可知聪聪有7本,所以5人的平均本数最接近聪聪的本数.
【解答】解:(7+13+6+4+5)÷5
=35÷5
=7(本)
由图可知聪聪有7本.
故选:A.
【点评】此题主要考查的是如何从统计图中获取信息,然后再根据信息解答问题即可.
6.【分析】由“两车间产值相差最大的那一季度一车间比二车间多40万元”与统计图,知道虚线的折线代表一车间全年的产值,2个格子表示40万元,所以1个格子表示20万元,由此得出一车间一季度的产值是20万元,二季度的产值是40万元,三季度的产值是60万元,四季度的产值是80万元,把四个季度的产值加起来就是一车间全年的产值.
【解答】解:因为2个格子表示40万元,所以1个格子表示20万元,
一车间全年产值:20+40+60+80=200(万元),
答:一车间全年产值200万元.
故选:D.
【点评】关键是根据题中的条件,得出1个格子代表的数值,再找出一车间各个季度的产值,列式解答即可.
7.【分析】通过看图可知,1月份的产量是60台,2月份是180台,3月份是150台,车床产量的整体趋势是先上升后下降,据此解答即可.
【解答】解:1月份的产量是60台,2月份是180台,3月份是150台,车床产量的整体趋势是先上升后下降.
故选:C。
【点评】本题是考查如何从折线统计图中获取信息.
8.【分析】由统计表可知:一月份的电话费是49元,二月份的电话费是52元,三月份的电话费是42元,四月份的电话费是47元;由此对五月份的电话费进行预测.
【解答】解:1﹣4月的电话费都在50元左右,那么5月份的电话费最有可能在这一范围.
故选:C.
【点评】先通过已知的数据对每月的电话费的范围有个大致的了解,再从选项中选出和这个范围相近的选项即可.
二.填空题(共10小题)
9.【分析】(1)根据条形统计图和扇形统计图中的数据可知:2015年该商场
其他类营业额最多,食品类营业额最少,分别占年营业额的
31.7%、19.5%.
(2)由折线统计图的特点可知:折线较陡的2009~2011年两年间该商场的营业额增长最快.
(3)把2009年的营业额看作单位“1”,求2013年比2019年营业额增长百分之几,就是求2013年营业额比2009年多的占2009年的百分之几.利用求一个数是另一个数的百分之几,用除法计算.把数代入计算即可.
(4)用2015年家电类营业额和食品类营业额求和即可求出“2015年该商场家电类和食品类的总营业额”;用2015年该商场家电类营业额减掉服装类营业额,即“服装类营业额比家电类营业额少”的数量.
【解答】解:(1)2015年该商场
其他类营业额最多,食品类营业额最少,分别占年营业额的
31.7%、19.5%.
(2)2009~2011两年间该商场的营业额增长最快.
(3)(320﹣160)÷160
=160÷160
=100%
答:2013年该商场的营业额比2009年增长了
100%.
(4)110+80=190(万元)
110﹣90=20(万元)
答:2015年该商场家电类和食品类的总营业额是
190万元,服装类营业额比家电类营业额少
20万元.
故答案为:其他;食品;31.7;19.5;2009;2011;100;190;20.
【点评】本题主要考查从统计图表中获取信息,关键根据统计表中的信息解决问题.
10.【分析】根据捐款5元占总数的百分比30%以及5元的人数15人,用15除以30%即可求出该班捐款的总人数.
【解答】解:15÷30%=50(人)
答:该班捐款的总人数是50人.
故答案为:50.
【点评】本题考查了条形统计图以及扇形统计图的有关知识.
11.【分析】根据条形统计图知道,上半年的条形图在横轴的上面,对应的数据是30万元,表示王叔叔上半年盈利30万元,下半年的条形图在横轴的下面,对应的数据是﹣20万元,表示王叔叔下半年亏损20万元;由此判断这一年王叔叔盈利(30﹣20)万元.
【解答】解:(1)由统计图知道:王叔叔下半年亏损20万元,
(2)30﹣20=10(万元),
答:下半年亏损20万元,这一年王叔叔盈利10万元.
故答案为:20、盈利.
【点评】关键是会看条形统计图,知道横轴上面的数据与横轴下面的数据表示的是相反意义的量.
12.【分析】(1)求九月销量比八月下降百分之几,也就是求九月比八月下降了的占八月份销量的百分之几;
(2)先求出商店五个月的总销售量,进而求得营业额,再求出税后收入即可;
(3)根据各个月游泳衣的销量提出建议即可求解.
【解答】解:(1)(160﹣80)÷160×100%
=80÷160×100%
=50%
答:九月销量比八月下降50%.
(2)(60+90+150+160+80)×50×(1﹣8%)
=540×50×92%
=27000×0.92
=24840(元)
答:商店五个月营业额的税后收入是24840元.
(3)建议:七月和八月多进游泳衣.
故答案为:50;24840;七月和八月多进游泳衣.
【点评】解答本题的关键是能从统计图中获取与问题有关的信息,再根据基本的数量关系解决问题.
13.【分析】(1)在这个扇形统计图中,用整个圆表示某班同学.
(2)通过观察可知:优的人最多,不及格
的人最少.
(3)成绩优秀的人数等于总人数乘以优秀率;
成绩良的人数等于总人数乘以中等的百分比;
【解答】解:(1)在这个扇形统计图中,用整个圆表示某班同学.
(2)通过观察可知:优的人最多,不及格
的人最少.
(3)60×60%=36(人)
60×25%=15(人)
答:得优的有36人,得良的有15人.
故答案为:某班同学,优,不及格,36,15.
【点评】此题主要考查的是如何观察扇形统计图并且从统计图中获取信息,然后再进行计算、解答即可.
14.【分析】扇形统计图中表示某部分的扇形占整体的百分之几,其圆心角就是占圆周角(360°)的百分之几.
【解答】解:360°×30%=108°.
故答案为:108.
【点评】此题是考查扇形统计图的意义及制作.看作扇形统计图关键是确定扇形圆心角的度数,扇形点整体的百分之几,其圆心角就是占360°的百分之几.
15.【分析】根据百分数乘法的意义,用牛奶的克数乘蛋白质所占的百分率就是蛋白质的克数.
【解答】解:500×4.2%=21(g)
答:500g牛奶中含蛋白质21g.
故答案为:21.
【点评】此题是考查如何从扇形统计图中获取信息,并根据所获取的信息进行有关计算.
16.【分析】①把小辉家的总支出看作单位“1”,减去服装、饮食、文化、旅游的支出之和,求出其他支出占总支出的百分比,除以服装支出占的百分比就是其他支出占总服装支出的百分比;
②将服装、饮食、文化三项支出的比化简即可;
③用旅游支出除以它所占的百分比,求出总支出,再用总支出乘文化、其它所占的百分比,解决问题.
【解答】解:①1﹣(10%+30%+25%+15%)
=1﹣80%
=20%;
20%÷10%=200%;
答:其他支出占总服装支出的2倍.
②10%:30%:25%=2:6:5
答:服装、饮食、文化三项支出的比是2:6:5.
③3000÷15%=20000(元)
20000×25%=5000(元)
20000×20%=4000(元);
答:总支出为20000元,文化支出为5000元,其它支出为4000元.
故答案为:200%,2:6:5,5000,4000,20000.
【点评】本题根据扇形统计图的特点,找出单位“1”,再根据基本的数量关系求解.
17.【分析】喜欢篮球的人数占总人数的40%,喜欢跳绳的人数占总人数的25%,那么喜欢篮球的人数百分比减去喜欢跳绳的人数的百分比对应的数量是150人,根据百分数除法的意义,用喜欢篮球的人数比喜欢跳绳的人数多的人数除以所占的百分率就是调查的总人数.
【解答】解:150÷(40%﹣25%)
=150÷15%
=1000(人)
答:这次一共调查了1000人.
故答案为:1000.
【点评】此题是考查如何从扇形统计图中获取信息,并根据所获取的信息解决实际问题.
18.【分析】扇形统计图是用整个圆表示总数或整体(单位“1”),用圆内各个扇形的大小表示各部分量占总量的百分之几,通过扇形统计图可以很清楚地表示出各部分数量与总数之间的关系.
【解答】解:扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分占总数的百分比.
故答案为:整个圆,圆内各个扇形.
【点评】此题主要是考查扇形统计图的意义及特征,扇形统计图的特征就是清楚的表示出各部分和整体(或总数、单位“1”)之间的关系.
三.判断题(共5小题)
19.【分析】把这个班喜欢各类活动的总人数看作单位“1”,即100%,用100%减去喜欢球类、美术类、其他类人数所占的百分率就是喜欢舞蹈类的占的百分率.
【解答】解:100%﹣35%﹣15%﹣40%=10%,
答:喜欢舞蹈类的占10%.
故答案为:×.
【点评】本题是考查根据扇形统计图所提供的信息进行有关计算.
20.【分析】根据扇形统计图中参加各兴趣小组人数所占的百分率或参加各兴趣小组人数所占扇形面积的大小,即可确定参加哪个兴趣小组的人数最多.
【解答】解:由扇形统计图可以看出:
参加歌咏小组的人数占40%,参加美术小组的人数占30,参加科技小组的人数占25%,参加书法小组的人数占5%,
40%>30%>25%>5%
歌咏小组的人数最多.
故答案为:√.
【点评】本题是考查如何从扇形统计图中获取信息,并对所获取的信息进行整理、分析,从中解决有关问题.
21.【分析】在扇形统计图中,表示部分的扇形占整个圆的百分之几,所对应的圆心角就是360°的百分之几.根据百分数乘法的意义即可求出表示占整体30%的扇形圆心角的度数.
【解答】解:360°×30%=108°
答:表示食品支出的扇形的圆心角是108°.
原题说法错误.
故答案为:×.
【点评】在扇形统计衅中有一个圆表示整体,扇形表示部分,部分占整体的百分之几,表示部分的扇形所对应的圆心角就是360°的百分之几.
22.【分析】把良好的人数看作单位“1”,先求出及格的人数比良好的人数少总人数百分之几,再根据求一个数是另一个数的百分之几,用除法求出及格的人数比良好的人数少百分之几,然后与15%进行比较即可。
【解答】解:(40%﹣25%)÷40%
=15%÷40%
=0.15÷0.4
=0.375
=37.5%
37.5%≠15%
答:及格的人数比良好的人数少37.5%。
故答案为:×。
【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
23.【分析】扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚的表示出各部分数量同总数之间的关系.
【解答】解:扇形统计图可直观看出统计数据各部分占总体的比率.
原题说法是正确的.
故答案为:√.
【点评】本题考查了扇形统计图的特点:扇形统计图能清楚地反映出各部分数同总数之间的关系与比例.
四.应用题(共4小题)
24.【分析】(1)根据喜欢乒乓球的有16人,占总数的32%,用除法即可求出总人数;然后求出喜欢足球的人数,进而求出比;
(2)用喜欢乒乓球的百分比减去喜欢篮球人数的百分比,再除以喜欢篮球人数的百分比,据此解答.
【解答】解:(1)16÷32%=50(人)
50×26%=13(人)
喜欢乒乓球与喜欢足球的人数比是:16:13.
答:喜欢乒乓球与喜欢足球的人数比是16:13.
(2)(32%﹣18%)÷18%×100%
=0.14÷0.18×100%
≈77.8%
答:喜欢乒乓球的比喜欢篮球的人多77.8%.
【点评】此题主要考查的是如何观察扇形统计图并且从统计图中获取信息.
25.【分析】根据求平均数的方法,用数据的总和除以数据的个数就是这组数据的平均数,把喜欢音乐、美术的平均分进行比较即可得出哪个科目更受欢迎.
【解答】解:(3+2+5+1+3+2+5+3)÷8
=24÷8
=3(分)
(5+3+4+4+5+2+4+5)÷8
=32÷8
=4(分)
3<4
所以美术更受欢迎;
答:美术更受欢迎.
【点评】此题考查的目的是理解平均数的意义,掌握求平均数的方法及应用.
26.【分析】(1)根据条形统计图,可以看出成绩是优秀的有12人,及格的有8人,先计算出优秀人数比及格人数多的人数,再除以及格的人数即可得解;
(2)根据及格的有8人,以及扇形统计图及格的占总测试人数的20%,可求出测试人数为8÷20%=40(人);
(3)先根据优秀人数即测试总人数,求优秀率,然后用总人数单位“1”分别减去优秀人数、良好人数、及格人数所占的百分率,就是不及格人数占的百分率;
(4)先计算出及格人数、不及格人数占总人数的百分率,在扇形统计图上标出,进而用总人数分别乘上良好和不及格人数占的百分率,再在条形统计图上标出即可.
【解答】解:(1)(12﹣8)÷8
=4÷8
=50%
答:优秀人数比及格人数多
50%.
(2)测试人数为:8÷20%=40(人);
答:六年级1班有
40人参加本次数学测试.
(3)优秀率为:12÷40=30%;
1﹣45%﹣20%﹣30%=5%
答:本次测试的优秀率是
30%,不及格占本班测试人数的5%.
(4)40×45%=18(人)
40×5%=2(人)
如图所示:
故答案为:50、40、40%、5.
【点评】解答此题的关键利用图中已知的信息,结合给出的条件,求得各部分数据解决问题.
27.【分析】(1)把六(2)班的学生总人数看作单位“1”,根据减法的意义,用减法解答。
(2)把六(2)班的学生总人数看作单位“1”,喜欢乒乓球的小数人数占全班人数的30%,根据一个数乘百分数的意义,用乘法解答。
【解答】解:1﹣25%﹣18%﹣5%﹣30%=22%
答:喜欢足球的占22%。
(2)60×30%=18(人)
答:喜欢乒乓球的有18人。
【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
五.操作题(共3小题)
28.【分析】用第一季度的销售额除以全年的总销售额就是第一季度销售额所占的百分率.根据第一季度销售额所占的百分率即可确定表示第一季度销售额的扇形大小.把全年的销售额看作单位“1”,用1减第一、第三、第四季度销售额所占的百分率就是第二季度销售额所占的百分率.
【解答】解:第一季度销售额所占的百分率:408÷1200=0.34=34%
第二季度销售额所占的百分率:1﹣34%﹣22%﹣20%=24%
根据以上信息完成扇形统计图如下:
【点评】此题主要是考查如何从扇形统计图中获取信息,然后再根据所获取的信息进一步完善扇形统计图.
29.【分析】此题要先求出总人数,然后利用除法求出各种等级占总人数的百分比,再标出相应的百分比即可.
【解答】解:总人数:12+16+10+2=40(人)
优占的百分比:12÷40=30%
良占的百分比:16÷40=40%
及格占的百分比:10÷40=25%
不及格占的百分比:2÷40=5%
如下图所示:
【点评】本题求出各部分占总体的百分比,然后根据圆分成的份数在圆中标出各百分比是重点,需要熟练掌握.
30.【分析】①从条形统计图中找出最喜欢的学科:语文:男生3人,女生4人;数学:男生8人,女生5人;体育:男生6人,女生4人;音乐:男生2人,女生3人,求出喜欢学科的总人数;
②用喜欢数学的男生人数减喜欢数学的女生人数,再除以喜欢数学的女生人数即可;
③把喜欢各个学科的男生人数相加即可.
【解答】解:①3+4+8+5+6+4+2+3
=15+5+6+4+2+3
=35(名),
答:一共调查了35名同学.
②(8﹣5)÷5
=3÷5
=60%,
答:喜欢数学的男生比女生多60%.
③3+8+6+2
=11+6+2
=19(人)
答:参与调查的男生共19人.
故答案为:①35;②60;③19.
【点评】解答此题的关键是,会看复式条形统计图,能够从中获取有用的信息,再根据各个题目的要求,选择合适的计算方法解答.
六.解答题(共1小题)
31.【分析】(1)①根据百分数大小比较的方法,把把同学们喜欢各种球类的人数所占的百分数进行比较即可。
②因为喜欢乒乓球的学生人数最多,所以组织学生观看乒乓球比赛。
(2)答案不唯一。提出的问题是:喜欢足球的有多少人?根据一个数乘百分数的意义,用乘法解答。
【解答】解:(1)①32%>25%>19%>18%>6%
32%+25%=57%
答:最受欢迎的两种球类活动是乒乓球和足球,它们的百分比之和是57%。
②因为喜欢乒乓球的学生人数最多,所以我会组织学生观看乒乓球比赛。
(2)答案不唯一。喜欢足球的有多少人?
1000×25%=250(人)
答:喜欢足球的有250人。
故答案为:乒乓球、足球、57%;乒乓球。
【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
奥运奖牌—扇形统计图》单元测试题
一.选择题(共8小题)
1.如图是六(3)和六(4)两个班级男、女生人数统计图,下列说法正确的是( )
A.六(4)班的男生比六(3)班的男生少
B.六(4)班的女生比六(3)班的女生多
C.六(4)班的学生比六(3)班的学生多
D.根据现在数据,不同班级间无法比较
2.某公司有员工700人,元旦要举行活动,如图是分别参加活动的人数的百分比,规定每人只允许参加一项且每人均参加,则不下围棋的人共有( )
A.259人
B.441人
C.350人
D.490人
3.某中学七年级二班学生有32%的同学喜欢打乒乓球,有68%的同学喜欢其他球类活动,若将上述情况画成一个扇形统计图,表示喜欢乒乓球的扇形的圆心角等于( )
A.120°
B.105.2°
C.115.2°
D.115°
4.小红从家去图书馆借书,中途休息了几分钟,借完书后直接回家.下面正确描述小红这一过程的图象是( )
A.
B.
C.
D.
5.下图是5个小朋友有课外书本数的统计图.5人的平均本数最接近哪个小朋友的本数?( )
A.聪聪
B.明明
C.丁丁
D.冬冬
E.乐乐
6.如图是某厂甲、乙两个车间2007后得季度产值的折线统计图,已知两车间产值相差最大的那一季度一车间比二车间多40万元,则一车间全年产值( )万元.
A.100
B.120
C.160
D.200
7.从折线统计图看,车床产量的整体趋势是( )
A.上升
B.下降
C.先上升后下降
8.李老师家2005年1﹣4月份座机电话费(不含上网费用)如下表:
月份
一
二
三
四
话费(元)
49
52
42
47
根据表中数据作出预测,李老师家今年五月份座机话费(不含上网费用)可能是( )
A.不超过12元
B.超过200元
C.50元左右
二.填空题(共10小题)
9.下面是某商场营业额情况统计图.
(1)2015年该商场
类营业额最多,
类营业额最少,分别占年营业额的
%、
%.
(2)
~
两年间该商场的营业额增长最快.
(3)2013年该商场的营业额比2009年增长了
%.
(4)2015年该商场家电类和食品类的总营业额是
万元,服装类营业额比家电类营业额少
万元.
10.雅安地震,牵动着全国人民的心,地震后某学校举行了爱心捐款活动,如图是该校某班学生为雅安灾区捐款情况绘制的不完整的条形统计图和扇形统计图.由统计图可知该班人数为
人.
11.如图反映了某一年中王叔叔做生意收入情况.从图中可知王叔叔上半年盈利30万元,下半年亏损
万元,这一年王叔叔
10万元.
12.看统计图回答问题.
(1)九月销量比八月下降
%.
(2)每件游泳衣售价50元,按8%的税率缴纳营业税,商店五个月营业额的税后收入是
元.
(3)如果你是该商店的销售员,你对明年游泳衣的进货量的建议是
.
13.如图是某班同学期末考试成绩统计图.
根据统计图,完成下面问题.
(1)在这个扇形统计图中,用整个圆表示
.
(2)
的人最多,
的人最少.
(3)如果这个班有60人,那么得优的有
人,得良的有
人.
14.实验小学喜欢乒乓球的人数占总人数的30%,如果制作扇形统计图,喜欢乒乓球的人数所表示扇形的圆心角应是
度.
15.一种牛奶每100g中所含营养成分如图所示,500g牛奶中含蛋白质
g.
16.如图是小辉家去年各项支出的统计图.其中其他支出占总服装支出的
,服装、饮食、文化三项支出的比是
.如果旅游支出为3000元,那么文化支出为
元,其他支出为
元,总支出为
元.
17.如果喜欢篮球的人数比喜欢跳绳的人数多150人,那么这次一共调查了
人.
18.扇形统计图用
表示总数,用
的面积表示各个部分量占总数的百分比.
三.判断题(共5小题)
19.如图是六一班喜欢各类活动的统计图,其中喜欢舞蹈类的占20%.
(判断对错)
20.如图是某校同学参加课外兴趣小组,其中参加歌咏小组的人数最多.
(判断对错)
21.晶晶家5月份食品支出占生活总支出的30%,在制作扇形统计图时,表示食品支出的扇形的圆心角是30°.
(判断对错)
22.如图中,及格的人数比良好的人数少15%.
(判断对错)
23.扇形统计图可直观看出统计数据各部分占总体的比率.
.(判断对错)
四.应用题(共4小题)
24.如图是向阳小学六(1)班同学最喜欢体育项目情况的统计图.
①如果喜欢乒乓球的有16人,那么喜欢乒乓球与喜欢足球的人数比是多少?
②喜欢乒乓球的比喜欢篮球的人多百分之几?
25.一个8人小组想知道他们小组更喜欢音乐还是美术,于是他们用1、2、3、4、5分别表示非常不喜欢、不喜欢、一般、喜欢、非常喜欢,结果如表.
学生1
学生2
学生3
学生4
学生5
学生6
学生7
学生8
音乐
3
2
5
1
3
2
5
3
美术
5
3
4
4
5
2
4
5
你认为哪个科目更受欢迎?
26.下面两图,是根据某校六年级(1)班一次数学测试成绩数据绘制成的统计图,请结合两幅统计图提供的信息,回答下面问题.
(1)列式计算出六年级(1)班数学测试成绩优秀人数比及格人数多百分之几?
(2)列式计算出六年级(1)班有多少人参加本次数学测试?
(3)列式计算不及格人数占六年级(1)班测试总人数的百分之几?
(4)把条形统计图和扇形统计图补充或填写完整.
27.如图是实验小学六(2)班同学最喜欢的一项球类活动调查统计图。
(1)喜欢足球的占百分之几?
(2)如果六(2)班有60人,那么喜欢乒乓球的有多少人?
五.操作题(共3小题)
28.某商场2018年销售总额是1200万元.其中第一季度销售额是408万元.根据上述信息,完成如图统计图.
29.六(2)班上学期期末的体育成绩得优的有12人,得良的有16人,及格的有10人,不及格的有2人,利用如图的图形,制成扇形统计图,分别表示不同成绩人数各占全班人数的百分之几.
30.淘气把调查的六一班同学最喜欢的学科的情况制成了下面的统计图.从图中可以看出.
①一共调查了
名同学.
②喜欢数学的男生比女生多
%.
③参与调查的男生共
人.
六.解答题(共1小题)
31.如图是某校同学喜欢的球类运动统计图。
(1)观察上面的扇形统计图,回答问题。
①最受欢迎的两种球类活动是
和
,它们的百分比之和是
。
②如果你是体育委员,准备组织全班同学去观看球类比赛。为了吸引尽可能多的同学参与,你会组织观看
比赛。
(2)如果这个学校共有学生1000名,请你根据统计图提出一个数学问题并解答。
参考答案与试题解析
一.选择题(共8小题)
1.【分析】由第一个图可知:六(3)班的总人数是单位“1”男生占54%,女生占46%;
由第二个图可知:六(4)班的总人数是单位“1”,男生占52%,女占48%;由此求解;
【解答】解:两个图的单位“1”不相同,一个是六(3)班的总人数,一个是六(4)班的总人数;
而两个班的各有多少人未知,它们的百分之几是多少就无法求解,两个班之间的人数就无法比较.
故选:D.
【点评】解决本题关键是找出两个图它们的单位“1”不同,两个班的总人数未知,无法比较两个班之间的人数多少.
2.【分析】不下围棋的人数的百分比是1﹣37%,不下围棋的人共有700×(1﹣37%)人,即可得解.
【解答】解:700×(1﹣37%)
=700×63%
=441(人)
答:不下围棋的人共有441人.
故选:B.
【点评】此题主要考查的是如何观察扇形统计图并且从统计图中获取信息,然后再进行计算、解答即可.
3.【分析】一个扇形统计图的总圆心角是360°,有32%的同学喜欢打乒乓球,求表示喜欢乒乓球的扇形的圆心角等于多少用乘法,即可得解.
【解答】解:360×32%=115.2°,
答:表示喜欢乒乓球的扇形的圆心角等于115.2°;
故选:C.
【点评】扇形统计图是用整个圆表示总数(单位“1”),用圆内各个扇形的大小表示各部分量占总数量的百分之几,扇形统计图中各部分的百分比之和等于“1”.通过扇形统计图可以很清楚地表出各部分数量同总数之间的关系,而不是反应变化趋势.
4.【分析】根据所给的条件,分析出时间与离家距离之间的关系,再从选项中找出符合的答案.
【解答】解:小红的这一过程可分成以下几段:
(1)从家出发到途中休息前,这一段时间里离家的距离越来越远;
(2)途中休息,这一段时间离家的距离不变;
(3)途中休息后到图书馆,这一段时间里离家的距离越来越远;
(4)在图书馆借书,这一段时间离家的距离不变;
(5)从图书馆回家,这一段时间里离家的距离越来越近.
只有选项C符合这一变化.
故选:C.
【点评】这类题目关键是找出离家的距离随时间的变化是怎么变化的,分好段求解.
5.【分析】通过观察可知:这5个小朋友的课外书的数量是7+13+6+4+5=35本,每个小朋友平均有:35÷5=7本,由图可知聪聪有7本,所以5人的平均本数最接近聪聪的本数.
【解答】解:(7+13+6+4+5)÷5
=35÷5
=7(本)
由图可知聪聪有7本.
故选:A.
【点评】此题主要考查的是如何从统计图中获取信息,然后再根据信息解答问题即可.
6.【分析】由“两车间产值相差最大的那一季度一车间比二车间多40万元”与统计图,知道虚线的折线代表一车间全年的产值,2个格子表示40万元,所以1个格子表示20万元,由此得出一车间一季度的产值是20万元,二季度的产值是40万元,三季度的产值是60万元,四季度的产值是80万元,把四个季度的产值加起来就是一车间全年的产值.
【解答】解:因为2个格子表示40万元,所以1个格子表示20万元,
一车间全年产值:20+40+60+80=200(万元),
答:一车间全年产值200万元.
故选:D.
【点评】关键是根据题中的条件,得出1个格子代表的数值,再找出一车间各个季度的产值,列式解答即可.
7.【分析】通过看图可知,1月份的产量是60台,2月份是180台,3月份是150台,车床产量的整体趋势是先上升后下降,据此解答即可.
【解答】解:1月份的产量是60台,2月份是180台,3月份是150台,车床产量的整体趋势是先上升后下降.
故选:C。
【点评】本题是考查如何从折线统计图中获取信息.
8.【分析】由统计表可知:一月份的电话费是49元,二月份的电话费是52元,三月份的电话费是42元,四月份的电话费是47元;由此对五月份的电话费进行预测.
【解答】解:1﹣4月的电话费都在50元左右,那么5月份的电话费最有可能在这一范围.
故选:C.
【点评】先通过已知的数据对每月的电话费的范围有个大致的了解,再从选项中选出和这个范围相近的选项即可.
二.填空题(共10小题)
9.【分析】(1)根据条形统计图和扇形统计图中的数据可知:2015年该商场
其他类营业额最多,食品类营业额最少,分别占年营业额的
31.7%、19.5%.
(2)由折线统计图的特点可知:折线较陡的2009~2011年两年间该商场的营业额增长最快.
(3)把2009年的营业额看作单位“1”,求2013年比2019年营业额增长百分之几,就是求2013年营业额比2009年多的占2009年的百分之几.利用求一个数是另一个数的百分之几,用除法计算.把数代入计算即可.
(4)用2015年家电类营业额和食品类营业额求和即可求出“2015年该商场家电类和食品类的总营业额”;用2015年该商场家电类营业额减掉服装类营业额,即“服装类营业额比家电类营业额少”的数量.
【解答】解:(1)2015年该商场
其他类营业额最多,食品类营业额最少,分别占年营业额的
31.7%、19.5%.
(2)2009~2011两年间该商场的营业额增长最快.
(3)(320﹣160)÷160
=160÷160
=100%
答:2013年该商场的营业额比2009年增长了
100%.
(4)110+80=190(万元)
110﹣90=20(万元)
答:2015年该商场家电类和食品类的总营业额是
190万元,服装类营业额比家电类营业额少
20万元.
故答案为:其他;食品;31.7;19.5;2009;2011;100;190;20.
【点评】本题主要考查从统计图表中获取信息,关键根据统计表中的信息解决问题.
10.【分析】根据捐款5元占总数的百分比30%以及5元的人数15人,用15除以30%即可求出该班捐款的总人数.
【解答】解:15÷30%=50(人)
答:该班捐款的总人数是50人.
故答案为:50.
【点评】本题考查了条形统计图以及扇形统计图的有关知识.
11.【分析】根据条形统计图知道,上半年的条形图在横轴的上面,对应的数据是30万元,表示王叔叔上半年盈利30万元,下半年的条形图在横轴的下面,对应的数据是﹣20万元,表示王叔叔下半年亏损20万元;由此判断这一年王叔叔盈利(30﹣20)万元.
【解答】解:(1)由统计图知道:王叔叔下半年亏损20万元,
(2)30﹣20=10(万元),
答:下半年亏损20万元,这一年王叔叔盈利10万元.
故答案为:20、盈利.
【点评】关键是会看条形统计图,知道横轴上面的数据与横轴下面的数据表示的是相反意义的量.
12.【分析】(1)求九月销量比八月下降百分之几,也就是求九月比八月下降了的占八月份销量的百分之几;
(2)先求出商店五个月的总销售量,进而求得营业额,再求出税后收入即可;
(3)根据各个月游泳衣的销量提出建议即可求解.
【解答】解:(1)(160﹣80)÷160×100%
=80÷160×100%
=50%
答:九月销量比八月下降50%.
(2)(60+90+150+160+80)×50×(1﹣8%)
=540×50×92%
=27000×0.92
=24840(元)
答:商店五个月营业额的税后收入是24840元.
(3)建议:七月和八月多进游泳衣.
故答案为:50;24840;七月和八月多进游泳衣.
【点评】解答本题的关键是能从统计图中获取与问题有关的信息,再根据基本的数量关系解决问题.
13.【分析】(1)在这个扇形统计图中,用整个圆表示某班同学.
(2)通过观察可知:优的人最多,不及格
的人最少.
(3)成绩优秀的人数等于总人数乘以优秀率;
成绩良的人数等于总人数乘以中等的百分比;
【解答】解:(1)在这个扇形统计图中,用整个圆表示某班同学.
(2)通过观察可知:优的人最多,不及格
的人最少.
(3)60×60%=36(人)
60×25%=15(人)
答:得优的有36人,得良的有15人.
故答案为:某班同学,优,不及格,36,15.
【点评】此题主要考查的是如何观察扇形统计图并且从统计图中获取信息,然后再进行计算、解答即可.
14.【分析】扇形统计图中表示某部分的扇形占整体的百分之几,其圆心角就是占圆周角(360°)的百分之几.
【解答】解:360°×30%=108°.
故答案为:108.
【点评】此题是考查扇形统计图的意义及制作.看作扇形统计图关键是确定扇形圆心角的度数,扇形点整体的百分之几,其圆心角就是占360°的百分之几.
15.【分析】根据百分数乘法的意义,用牛奶的克数乘蛋白质所占的百分率就是蛋白质的克数.
【解答】解:500×4.2%=21(g)
答:500g牛奶中含蛋白质21g.
故答案为:21.
【点评】此题是考查如何从扇形统计图中获取信息,并根据所获取的信息进行有关计算.
16.【分析】①把小辉家的总支出看作单位“1”,减去服装、饮食、文化、旅游的支出之和,求出其他支出占总支出的百分比,除以服装支出占的百分比就是其他支出占总服装支出的百分比;
②将服装、饮食、文化三项支出的比化简即可;
③用旅游支出除以它所占的百分比,求出总支出,再用总支出乘文化、其它所占的百分比,解决问题.
【解答】解:①1﹣(10%+30%+25%+15%)
=1﹣80%
=20%;
20%÷10%=200%;
答:其他支出占总服装支出的2倍.
②10%:30%:25%=2:6:5
答:服装、饮食、文化三项支出的比是2:6:5.
③3000÷15%=20000(元)
20000×25%=5000(元)
20000×20%=4000(元);
答:总支出为20000元,文化支出为5000元,其它支出为4000元.
故答案为:200%,2:6:5,5000,4000,20000.
【点评】本题根据扇形统计图的特点,找出单位“1”,再根据基本的数量关系求解.
17.【分析】喜欢篮球的人数占总人数的40%,喜欢跳绳的人数占总人数的25%,那么喜欢篮球的人数百分比减去喜欢跳绳的人数的百分比对应的数量是150人,根据百分数除法的意义,用喜欢篮球的人数比喜欢跳绳的人数多的人数除以所占的百分率就是调查的总人数.
【解答】解:150÷(40%﹣25%)
=150÷15%
=1000(人)
答:这次一共调查了1000人.
故答案为:1000.
【点评】此题是考查如何从扇形统计图中获取信息,并根据所获取的信息解决实际问题.
18.【分析】扇形统计图是用整个圆表示总数或整体(单位“1”),用圆内各个扇形的大小表示各部分量占总量的百分之几,通过扇形统计图可以很清楚地表示出各部分数量与总数之间的关系.
【解答】解:扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分占总数的百分比.
故答案为:整个圆,圆内各个扇形.
【点评】此题主要是考查扇形统计图的意义及特征,扇形统计图的特征就是清楚的表示出各部分和整体(或总数、单位“1”)之间的关系.
三.判断题(共5小题)
19.【分析】把这个班喜欢各类活动的总人数看作单位“1”,即100%,用100%减去喜欢球类、美术类、其他类人数所占的百分率就是喜欢舞蹈类的占的百分率.
【解答】解:100%﹣35%﹣15%﹣40%=10%,
答:喜欢舞蹈类的占10%.
故答案为:×.
【点评】本题是考查根据扇形统计图所提供的信息进行有关计算.
20.【分析】根据扇形统计图中参加各兴趣小组人数所占的百分率或参加各兴趣小组人数所占扇形面积的大小,即可确定参加哪个兴趣小组的人数最多.
【解答】解:由扇形统计图可以看出:
参加歌咏小组的人数占40%,参加美术小组的人数占30,参加科技小组的人数占25%,参加书法小组的人数占5%,
40%>30%>25%>5%
歌咏小组的人数最多.
故答案为:√.
【点评】本题是考查如何从扇形统计图中获取信息,并对所获取的信息进行整理、分析,从中解决有关问题.
21.【分析】在扇形统计图中,表示部分的扇形占整个圆的百分之几,所对应的圆心角就是360°的百分之几.根据百分数乘法的意义即可求出表示占整体30%的扇形圆心角的度数.
【解答】解:360°×30%=108°
答:表示食品支出的扇形的圆心角是108°.
原题说法错误.
故答案为:×.
【点评】在扇形统计衅中有一个圆表示整体,扇形表示部分,部分占整体的百分之几,表示部分的扇形所对应的圆心角就是360°的百分之几.
22.【分析】把良好的人数看作单位“1”,先求出及格的人数比良好的人数少总人数百分之几,再根据求一个数是另一个数的百分之几,用除法求出及格的人数比良好的人数少百分之几,然后与15%进行比较即可。
【解答】解:(40%﹣25%)÷40%
=15%÷40%
=0.15÷0.4
=0.375
=37.5%
37.5%≠15%
答:及格的人数比良好的人数少37.5%。
故答案为:×。
【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
23.【分析】扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚的表示出各部分数量同总数之间的关系.
【解答】解:扇形统计图可直观看出统计数据各部分占总体的比率.
原题说法是正确的.
故答案为:√.
【点评】本题考查了扇形统计图的特点:扇形统计图能清楚地反映出各部分数同总数之间的关系与比例.
四.应用题(共4小题)
24.【分析】(1)根据喜欢乒乓球的有16人,占总数的32%,用除法即可求出总人数;然后求出喜欢足球的人数,进而求出比;
(2)用喜欢乒乓球的百分比减去喜欢篮球人数的百分比,再除以喜欢篮球人数的百分比,据此解答.
【解答】解:(1)16÷32%=50(人)
50×26%=13(人)
喜欢乒乓球与喜欢足球的人数比是:16:13.
答:喜欢乒乓球与喜欢足球的人数比是16:13.
(2)(32%﹣18%)÷18%×100%
=0.14÷0.18×100%
≈77.8%
答:喜欢乒乓球的比喜欢篮球的人多77.8%.
【点评】此题主要考查的是如何观察扇形统计图并且从统计图中获取信息.
25.【分析】根据求平均数的方法,用数据的总和除以数据的个数就是这组数据的平均数,把喜欢音乐、美术的平均分进行比较即可得出哪个科目更受欢迎.
【解答】解:(3+2+5+1+3+2+5+3)÷8
=24÷8
=3(分)
(5+3+4+4+5+2+4+5)÷8
=32÷8
=4(分)
3<4
所以美术更受欢迎;
答:美术更受欢迎.
【点评】此题考查的目的是理解平均数的意义,掌握求平均数的方法及应用.
26.【分析】(1)根据条形统计图,可以看出成绩是优秀的有12人,及格的有8人,先计算出优秀人数比及格人数多的人数,再除以及格的人数即可得解;
(2)根据及格的有8人,以及扇形统计图及格的占总测试人数的20%,可求出测试人数为8÷20%=40(人);
(3)先根据优秀人数即测试总人数,求优秀率,然后用总人数单位“1”分别减去优秀人数、良好人数、及格人数所占的百分率,就是不及格人数占的百分率;
(4)先计算出及格人数、不及格人数占总人数的百分率,在扇形统计图上标出,进而用总人数分别乘上良好和不及格人数占的百分率,再在条形统计图上标出即可.
【解答】解:(1)(12﹣8)÷8
=4÷8
=50%
答:优秀人数比及格人数多
50%.
(2)测试人数为:8÷20%=40(人);
答:六年级1班有
40人参加本次数学测试.
(3)优秀率为:12÷40=30%;
1﹣45%﹣20%﹣30%=5%
答:本次测试的优秀率是
30%,不及格占本班测试人数的5%.
(4)40×45%=18(人)
40×5%=2(人)
如图所示:
故答案为:50、40、40%、5.
【点评】解答此题的关键利用图中已知的信息,结合给出的条件,求得各部分数据解决问题.
27.【分析】(1)把六(2)班的学生总人数看作单位“1”,根据减法的意义,用减法解答。
(2)把六(2)班的学生总人数看作单位“1”,喜欢乒乓球的小数人数占全班人数的30%,根据一个数乘百分数的意义,用乘法解答。
【解答】解:1﹣25%﹣18%﹣5%﹣30%=22%
答:喜欢足球的占22%。
(2)60×30%=18(人)
答:喜欢乒乓球的有18人。
【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
五.操作题(共3小题)
28.【分析】用第一季度的销售额除以全年的总销售额就是第一季度销售额所占的百分率.根据第一季度销售额所占的百分率即可确定表示第一季度销售额的扇形大小.把全年的销售额看作单位“1”,用1减第一、第三、第四季度销售额所占的百分率就是第二季度销售额所占的百分率.
【解答】解:第一季度销售额所占的百分率:408÷1200=0.34=34%
第二季度销售额所占的百分率:1﹣34%﹣22%﹣20%=24%
根据以上信息完成扇形统计图如下:
【点评】此题主要是考查如何从扇形统计图中获取信息,然后再根据所获取的信息进一步完善扇形统计图.
29.【分析】此题要先求出总人数,然后利用除法求出各种等级占总人数的百分比,再标出相应的百分比即可.
【解答】解:总人数:12+16+10+2=40(人)
优占的百分比:12÷40=30%
良占的百分比:16÷40=40%
及格占的百分比:10÷40=25%
不及格占的百分比:2÷40=5%
如下图所示:
【点评】本题求出各部分占总体的百分比,然后根据圆分成的份数在圆中标出各百分比是重点,需要熟练掌握.
30.【分析】①从条形统计图中找出最喜欢的学科:语文:男生3人,女生4人;数学:男生8人,女生5人;体育:男生6人,女生4人;音乐:男生2人,女生3人,求出喜欢学科的总人数;
②用喜欢数学的男生人数减喜欢数学的女生人数,再除以喜欢数学的女生人数即可;
③把喜欢各个学科的男生人数相加即可.
【解答】解:①3+4+8+5+6+4+2+3
=15+5+6+4+2+3
=35(名),
答:一共调查了35名同学.
②(8﹣5)÷5
=3÷5
=60%,
答:喜欢数学的男生比女生多60%.
③3+8+6+2
=11+6+2
=19(人)
答:参与调查的男生共19人.
故答案为:①35;②60;③19.
【点评】解答此题的关键是,会看复式条形统计图,能够从中获取有用的信息,再根据各个题目的要求,选择合适的计算方法解答.
六.解答题(共1小题)
31.【分析】(1)①根据百分数大小比较的方法,把把同学们喜欢各种球类的人数所占的百分数进行比较即可。
②因为喜欢乒乓球的学生人数最多,所以组织学生观看乒乓球比赛。
(2)答案不唯一。提出的问题是:喜欢足球的有多少人?根据一个数乘百分数的意义,用乘法解答。
【解答】解:(1)①32%>25%>19%>18%>6%
32%+25%=57%
答:最受欢迎的两种球类活动是乒乓球和足球,它们的百分比之和是57%。
②因为喜欢乒乓球的学生人数最多,所以我会组织学生观看乒乓球比赛。
(2)答案不唯一。喜欢足球的有多少人?
1000×25%=250(人)
答:喜欢足球的有250人。
故答案为:乒乓球、足球、57%;乒乓球。
【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
