六年级数学下册课件-2 圆柱和圆锥 -苏教版(共60张PPT)
文档属性
| 名称 | 六年级数学下册课件-2 圆柱和圆锥 -苏教版(共60张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-21 12:03:55 | ||
图片预览









文档简介
(共60张PPT)
圆柱与圆锥整理与练习
圆柱的特征:
1.两个底面是半径相等的两个圆
2.圆柱有一个曲面叫做侧面,展
开后是一个长方形。
3.圆柱有无数条高,且高的
长度都相等
长=底面周长
宽=高
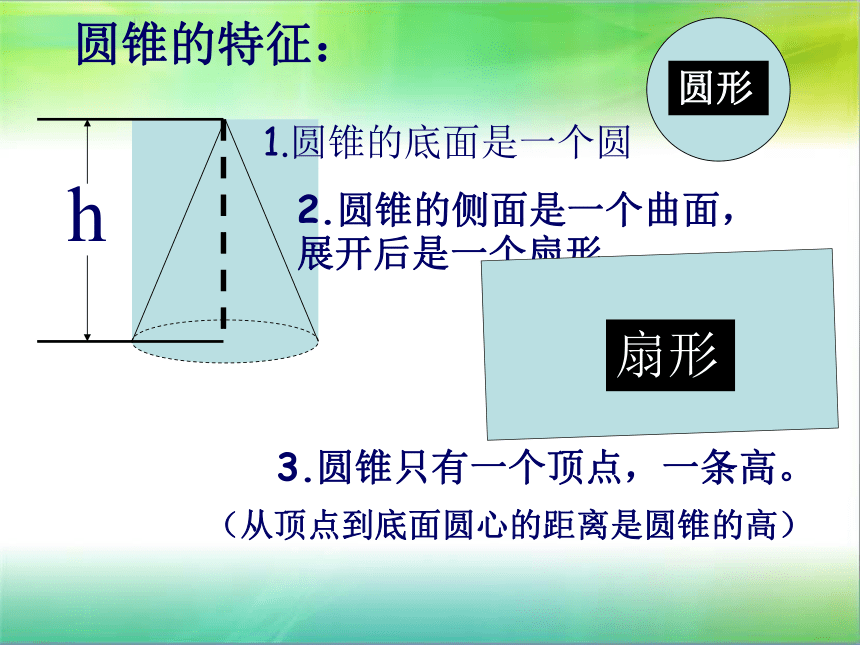
圆锥的特征:
h
1.圆锥的底面是一个圆
圆形
2.圆锥的侧面是一个曲面,
展开后是一个扇形
扇形
3.圆锥只有一个顶点,一条高。
(从顶点到底面圆心的距离是圆锥的高)
基本公式
圆柱侧面积=
圆柱表面积=
圆柱体积=
圆锥体积=
底面周长×高
侧面积+底面积×
2
底面积×高
底面积×高×
V=sh=Πr2h
V=
sh=
Πr2h
圆柱与圆锥的体积之间有什么关系?
等底等高圆锥体积是圆柱体积的
三分之一
等底等高圆柱体积是圆锥体积的3倍
请回答下面的问题,并列出算式。
一个圆柱形水桶,底面半径10分米,
高是20分米。
①给这个水桶加个盖,是求哪个部分?
②给这个水桶加个箍,是求哪个部分?
③给这个水桶的外面涂上油漆,是求哪个部分?
④这个水桶能装多少水,是求哪个部分?
压路机前轮直径0.8米,轮宽1.6米,前轮转一周,可以压路多少平方米?
πx0.8x1.6=1.28
π(平方米)
4
①S侧=ch
=π×4×5
=20π
③S表=
S侧+
2S底
=20π+4π×2
=20π+8π
=28π
②S底=πr?
=π×2?
=4π
28π㎝?
V=sh
=4π×5
=20π
20π㎝?
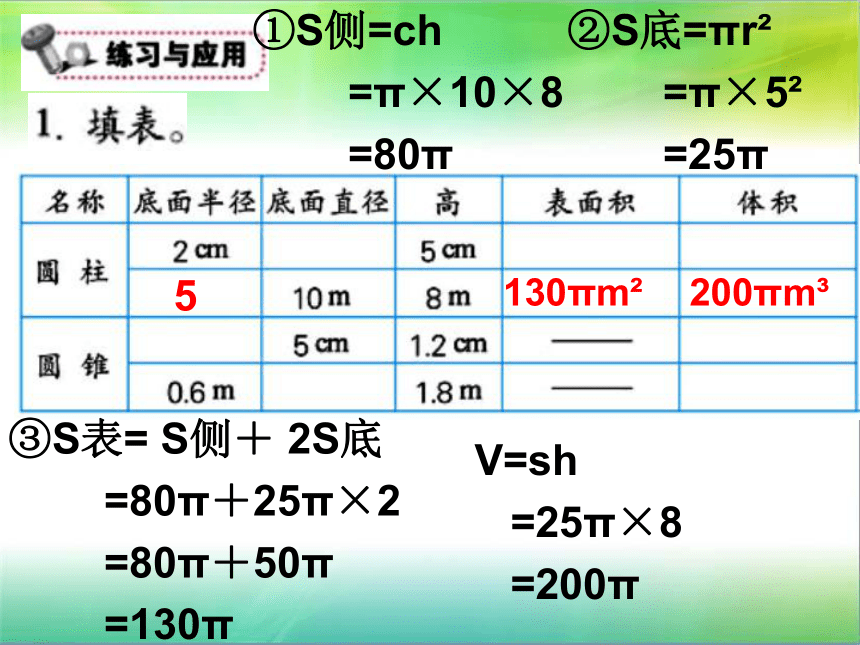
①S侧=ch
=π×10×8
=80π
③S表=
S侧+
2S底
=80π+25π×2
=80π+50π
=130π
②S底=πr?
=π×5?
=25π
V=sh
=25π×8
=200π
5
130πm?
200πm?
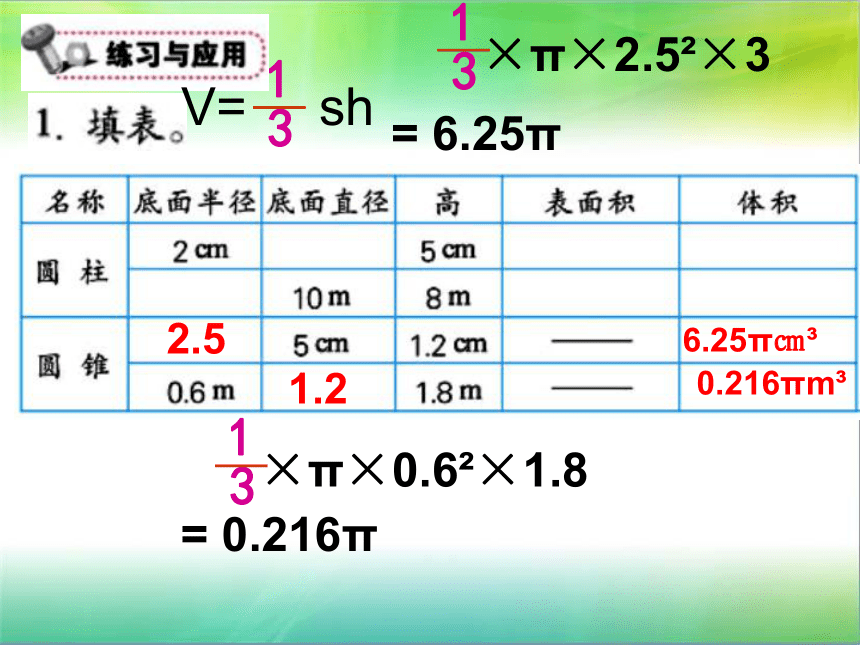
2.5
6.25π㎝?
V=
sh
1
3
1
3
×π×2.5?×3
=
6.25π
1.2
1
3
×π×0.6?×1.8
=
0.216π
0.216πm?
S侧=ch
=π×0.8×1.6
=1.28π
底面周长
侧面积+1底面积
容积
①S侧=ch
=15.7×6
=94.2
③
94.2+19.625
=113.825(dm?)
②S底=πr?
=3.14×(15.7÷3.14÷2)?
=19.625
V=sh
=19.625×6
=117.75
第
二
课
时
基本公式
圆柱侧面积=
圆柱表面积=
圆柱体积=
圆锥体积=
底面周长×高
侧面积+底面积×
2
底面积×高
底面积×高×
V=sh=Πr2h
V=
sh=
Πr2h
1.甲乙两人分别利用一张长20厘米,
宽15厘米的纸用两种不同的方法围成一个圆柱体(接头处不重叠),那么围成的圆柱(
)。
A、高一定相等
B、侧面积一定相等
C、侧面积和高都相等
D、侧面积和高都不相等
20厘米
15厘米
1.甲乙两人分别利用一张长20厘米,
宽15厘米的纸用两种不同的方法围成一个圆柱体(接头处不重叠),那么围成的圆柱(
)。
A、高一定相等
B、侧面积一定相等
C、侧面积和高都相等
D、侧面积和高都不相等
B
2.冬天护林工人给圆柱形的树干的下端涂防蛀涂料,那么粉刷树干的面积是指(
)。
A.底面积
B.侧面积
C.表面积
D.体积
B
3.下雨时,给打谷场上的圆锥形谷堆盖上塑料防雨布,所需防雨布的最小面积是指圆锥的(
)。
A.
表面积
B.体积
C.
侧面积
C
4.把一个圆柱在平坦的桌面上滚动,那么滚动的路线是(
)。
A
圆弧
B直线
C曲线
B
6.一个圆锥的体积是a立方米,和它等底等高的圆柱体的体积是(
)立方米。
A.
a÷3
B.
2a
C.
3a
D.
a的立方
C
7.一个圆柱形水池的容积是18.84立方米,池底直径是4米,水池的深度是(
)。
1.5m
18.84÷(2×2×3.14)=1.5m
4÷2=2m
8.一根圆柱形木材长20分米,把截成4个相等的圆柱体.
表面积增加了18.84平方分米.截后每段圆柱体积是(
)。
15.7dm3
9.一个圆柱的侧面积是12.56平方厘米,底面半径是2厘米,那么这个圆柱的体积是(
)。
12.56cm3
2×3.14×2
=
12.56(厘米)
12.56÷12.56
=
1(厘米)
3.14
×
2
×
2
=12.56(平方厘米)
12.56
×
1
=
12.56(立方厘米)
10.把一个棱长是2分米的正方体削成一个最大的圆柱体,它的侧面积是(
)平方厘米。
A.6.28
B.12.56
C.18.84
D.
1256
2
2
2
2×3.14×2
D
一根6米长的圆柱形木料锯成相等的3段,
表面积增加了15平方厘米,每一小段的
木料的体积是多少立方厘米?
解:每小段木料的长:
6÷3=2(m)=200(cm)
15÷4
×
200=750(cm?)
答:———————。
圆柱与圆锥等底等高,圆柱体积比
圆锥体积大36立方分米,圆柱与圆锥
体积各是多少?
解:圆锥体积:36÷2=18(dm?)
圆柱体积:18
×
3=54(
dm?)
答:——————。
一个圆锥形的沙堆,底面周长是31.4m,
高是7.2m,每立方米沙重1.5吨,如果用
一辆载重6吨的汽车来运,几次可以运完?
解:底面半径r=31.4÷3.14÷2=5(m)
沙堆的体积:
V=1/3
×
3.14
×
5?
×
7.2=188.4(m?)
188.4
×
1.5÷6≈48(次)
答:——————————。
将一个底面半径是3分米,高是6分米
的圆柱木料削成一个最大的圆锥,至少
要削去多少立方分米的木料?
解:3.14x3?x6x2/3=113.04(dm?)
答:——————。
补充练习
判断:
1.计算圆柱形油桶能装多少升油就是求这个油桶的容积。
2.圆柱底面直径扩大2倍,高不变,它的体积也扩大2倍。
3.圆柱的底面周长和高相等时,它的侧面展开图一定是正方形。
4.圆锥的体积是圆柱体积的三分之一。
5.求做一个圆柱形的通风管需要多少铁皮,就是求圆柱的表面积。
回答下面的问题,并列出算式:
一个圆柱形无盖的水桶,底面半径10分米,高20分米。
1.给这个水桶加个箍,是求什么?
2.求这个水桶的占地面积,是求什么?
3.做这样一个水桶用多少铁皮,是求什么?
4.这个水桶能装多少水,是求什么?
20cm
3dm
仔细观察这根木头,结合圆柱和圆锥的知识,以及我们的生活实际,展开你们想象的翅膀,看看你能提出什么样的问题。
20cm
3dm
1.把这个木头横着放,滚动一圈,滚动的面积是多少?
S=ch
=3.14X20X30
=1884(平方厘米)
20cm
3dm
2.把这根木头全都刷上油漆,刷油漆的面积有多大?
S=S侧+
S底X2
=3.14X20X30+
3.14X
(
20÷2
)2
X2
=1884
+
628
=2512(平方厘米)
20cm
3dm
3.这个木桩的体积是多少?
V=sh
=
3.14X
(
20÷2
)2
X30
=314
X30
=9420(立方分米)
20cm
3dm
4.把这个圆柱形的木桩削成最大的圆锥形,那么这个圆锥形的木桩体积是多少?
20cm
3dm
20cm
3dm
5.削掉部分占这个圆柱体积的
几分之几?
20cm
3dm
9dm
20cm
3dm
6.沿着底面直径把这个圆柱切开,那么,它的表面积增加了多少
?
7.把这个圆柱切成两段,它的表面积增加了多少?
切成两段后增加了两个横截面的面积,也就是两个圆的面积。
一根圆柱形木材长20分米,把它截成4个相等的圆柱体.
表面积增加了18.84平方分米.截后每段圆柱体积是多少立方分米?
一个圆柱高10厘米,接上4厘米的一段后,表面积增加了25.12平方厘米,求原来圆柱的体积是多少立方厘米?
一个酒瓶里面深30厘米,底面直径是8厘米,瓶里有酒深10厘米,把酒瓶塞紧后倒置(瓶口向下),这时酒深20厘米,你能算出酒瓶的容积是多少毫升来吗?
10
20
30
8
圆柱与圆锥整理与练习
圆柱的特征:
1.两个底面是半径相等的两个圆
2.圆柱有一个曲面叫做侧面,展
开后是一个长方形。
3.圆柱有无数条高,且高的
长度都相等
长=底面周长
宽=高
圆锥的特征:
h
1.圆锥的底面是一个圆
圆形
2.圆锥的侧面是一个曲面,
展开后是一个扇形
扇形
3.圆锥只有一个顶点,一条高。
(从顶点到底面圆心的距离是圆锥的高)
基本公式
圆柱侧面积=
圆柱表面积=
圆柱体积=
圆锥体积=
底面周长×高
侧面积+底面积×
2
底面积×高
底面积×高×
V=sh=Πr2h
V=
sh=
Πr2h
圆柱与圆锥的体积之间有什么关系?
等底等高圆锥体积是圆柱体积的
三分之一
等底等高圆柱体积是圆锥体积的3倍
请回答下面的问题,并列出算式。
一个圆柱形水桶,底面半径10分米,
高是20分米。
①给这个水桶加个盖,是求哪个部分?
②给这个水桶加个箍,是求哪个部分?
③给这个水桶的外面涂上油漆,是求哪个部分?
④这个水桶能装多少水,是求哪个部分?
压路机前轮直径0.8米,轮宽1.6米,前轮转一周,可以压路多少平方米?
πx0.8x1.6=1.28
π(平方米)
4
①S侧=ch
=π×4×5
=20π
③S表=
S侧+
2S底
=20π+4π×2
=20π+8π
=28π
②S底=πr?
=π×2?
=4π
28π㎝?
V=sh
=4π×5
=20π
20π㎝?
①S侧=ch
=π×10×8
=80π
③S表=
S侧+
2S底
=80π+25π×2
=80π+50π
=130π
②S底=πr?
=π×5?
=25π
V=sh
=25π×8
=200π
5
130πm?
200πm?
2.5
6.25π㎝?
V=
sh
1
3
1
3
×π×2.5?×3
=
6.25π
1.2
1
3
×π×0.6?×1.8
=
0.216π
0.216πm?
S侧=ch
=π×0.8×1.6
=1.28π
底面周长
侧面积+1底面积
容积
①S侧=ch
=15.7×6
=94.2
③
94.2+19.625
=113.825(dm?)
②S底=πr?
=3.14×(15.7÷3.14÷2)?
=19.625
V=sh
=19.625×6
=117.75
第
二
课
时
基本公式
圆柱侧面积=
圆柱表面积=
圆柱体积=
圆锥体积=
底面周长×高
侧面积+底面积×
2
底面积×高
底面积×高×
V=sh=Πr2h
V=
sh=
Πr2h
1.甲乙两人分别利用一张长20厘米,
宽15厘米的纸用两种不同的方法围成一个圆柱体(接头处不重叠),那么围成的圆柱(
)。
A、高一定相等
B、侧面积一定相等
C、侧面积和高都相等
D、侧面积和高都不相等
20厘米
15厘米
1.甲乙两人分别利用一张长20厘米,
宽15厘米的纸用两种不同的方法围成一个圆柱体(接头处不重叠),那么围成的圆柱(
)。
A、高一定相等
B、侧面积一定相等
C、侧面积和高都相等
D、侧面积和高都不相等
B
2.冬天护林工人给圆柱形的树干的下端涂防蛀涂料,那么粉刷树干的面积是指(
)。
A.底面积
B.侧面积
C.表面积
D.体积
B
3.下雨时,给打谷场上的圆锥形谷堆盖上塑料防雨布,所需防雨布的最小面积是指圆锥的(
)。
A.
表面积
B.体积
C.
侧面积
C
4.把一个圆柱在平坦的桌面上滚动,那么滚动的路线是(
)。
A
圆弧
B直线
C曲线
B
6.一个圆锥的体积是a立方米,和它等底等高的圆柱体的体积是(
)立方米。
A.
a÷3
B.
2a
C.
3a
D.
a的立方
C
7.一个圆柱形水池的容积是18.84立方米,池底直径是4米,水池的深度是(
)。
1.5m
18.84÷(2×2×3.14)=1.5m
4÷2=2m
8.一根圆柱形木材长20分米,把截成4个相等的圆柱体.
表面积增加了18.84平方分米.截后每段圆柱体积是(
)。
15.7dm3
9.一个圆柱的侧面积是12.56平方厘米,底面半径是2厘米,那么这个圆柱的体积是(
)。
12.56cm3
2×3.14×2
=
12.56(厘米)
12.56÷12.56
=
1(厘米)
3.14
×
2
×
2
=12.56(平方厘米)
12.56
×
1
=
12.56(立方厘米)
10.把一个棱长是2分米的正方体削成一个最大的圆柱体,它的侧面积是(
)平方厘米。
A.6.28
B.12.56
C.18.84
D.
1256
2
2
2
2×3.14×2
D
一根6米长的圆柱形木料锯成相等的3段,
表面积增加了15平方厘米,每一小段的
木料的体积是多少立方厘米?
解:每小段木料的长:
6÷3=2(m)=200(cm)
15÷4
×
200=750(cm?)
答:———————。
圆柱与圆锥等底等高,圆柱体积比
圆锥体积大36立方分米,圆柱与圆锥
体积各是多少?
解:圆锥体积:36÷2=18(dm?)
圆柱体积:18
×
3=54(
dm?)
答:——————。
一个圆锥形的沙堆,底面周长是31.4m,
高是7.2m,每立方米沙重1.5吨,如果用
一辆载重6吨的汽车来运,几次可以运完?
解:底面半径r=31.4÷3.14÷2=5(m)
沙堆的体积:
V=1/3
×
3.14
×
5?
×
7.2=188.4(m?)
188.4
×
1.5÷6≈48(次)
答:——————————。
将一个底面半径是3分米,高是6分米
的圆柱木料削成一个最大的圆锥,至少
要削去多少立方分米的木料?
解:3.14x3?x6x2/3=113.04(dm?)
答:——————。
补充练习
判断:
1.计算圆柱形油桶能装多少升油就是求这个油桶的容积。
2.圆柱底面直径扩大2倍,高不变,它的体积也扩大2倍。
3.圆柱的底面周长和高相等时,它的侧面展开图一定是正方形。
4.圆锥的体积是圆柱体积的三分之一。
5.求做一个圆柱形的通风管需要多少铁皮,就是求圆柱的表面积。
回答下面的问题,并列出算式:
一个圆柱形无盖的水桶,底面半径10分米,高20分米。
1.给这个水桶加个箍,是求什么?
2.求这个水桶的占地面积,是求什么?
3.做这样一个水桶用多少铁皮,是求什么?
4.这个水桶能装多少水,是求什么?
20cm
3dm
仔细观察这根木头,结合圆柱和圆锥的知识,以及我们的生活实际,展开你们想象的翅膀,看看你能提出什么样的问题。
20cm
3dm
1.把这个木头横着放,滚动一圈,滚动的面积是多少?
S=ch
=3.14X20X30
=1884(平方厘米)
20cm
3dm
2.把这根木头全都刷上油漆,刷油漆的面积有多大?
S=S侧+
S底X2
=3.14X20X30+
3.14X
(
20÷2
)2
X2
=1884
+
628
=2512(平方厘米)
20cm
3dm
3.这个木桩的体积是多少?
V=sh
=
3.14X
(
20÷2
)2
X30
=314
X30
=9420(立方分米)
20cm
3dm
4.把这个圆柱形的木桩削成最大的圆锥形,那么这个圆锥形的木桩体积是多少?
20cm
3dm
20cm
3dm
5.削掉部分占这个圆柱体积的
几分之几?
20cm
3dm
9dm
20cm
3dm
6.沿着底面直径把这个圆柱切开,那么,它的表面积增加了多少
?
7.把这个圆柱切成两段,它的表面积增加了多少?
切成两段后增加了两个横截面的面积,也就是两个圆的面积。
一根圆柱形木材长20分米,把它截成4个相等的圆柱体.
表面积增加了18.84平方分米.截后每段圆柱体积是多少立方分米?
一个圆柱高10厘米,接上4厘米的一段后,表面积增加了25.12平方厘米,求原来圆柱的体积是多少立方厘米?
一个酒瓶里面深30厘米,底面直径是8厘米,瓶里有酒深10厘米,把酒瓶塞紧后倒置(瓶口向下),这时酒深20厘米,你能算出酒瓶的容积是多少毫升来吗?
10
20
30
8
