四年级下册数学教案-8.2 平均数 西师大版
文档属性
| 名称 | 四年级下册数学教案-8.2 平均数 西师大版 |
|
|
| 格式 | doc | ||
| 文件大小 | 326.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-21 00:00:00 | ||
图片预览



文档简介
“平均数”教学设计
教学内容:西师版《义务教育教科书·数学》四年级下册第87-90页。
教学目标
1.在具体的问题情境中,感受引入平均数是统计和比较的需要,通过操作和思考体会平均数的意义,会求简单数据的平均数(结果是整数)。
2.能运用平均数的知识解释简单的生活现象,解决简单实际问题,进一步积累分析和处理数据的方法,发展统计观念。
3.进一步发展学生的思维能力,增强与同伴交流的意识与能力,体验运用知识解决问题的乐趣,建立学好数学的信心。
教学重点:理解平均数的特征。
教学难点:体会平均数的意义。
教学具准备:多媒体课件、练习纸。
教学过程:
一、创设情景,引出平均数
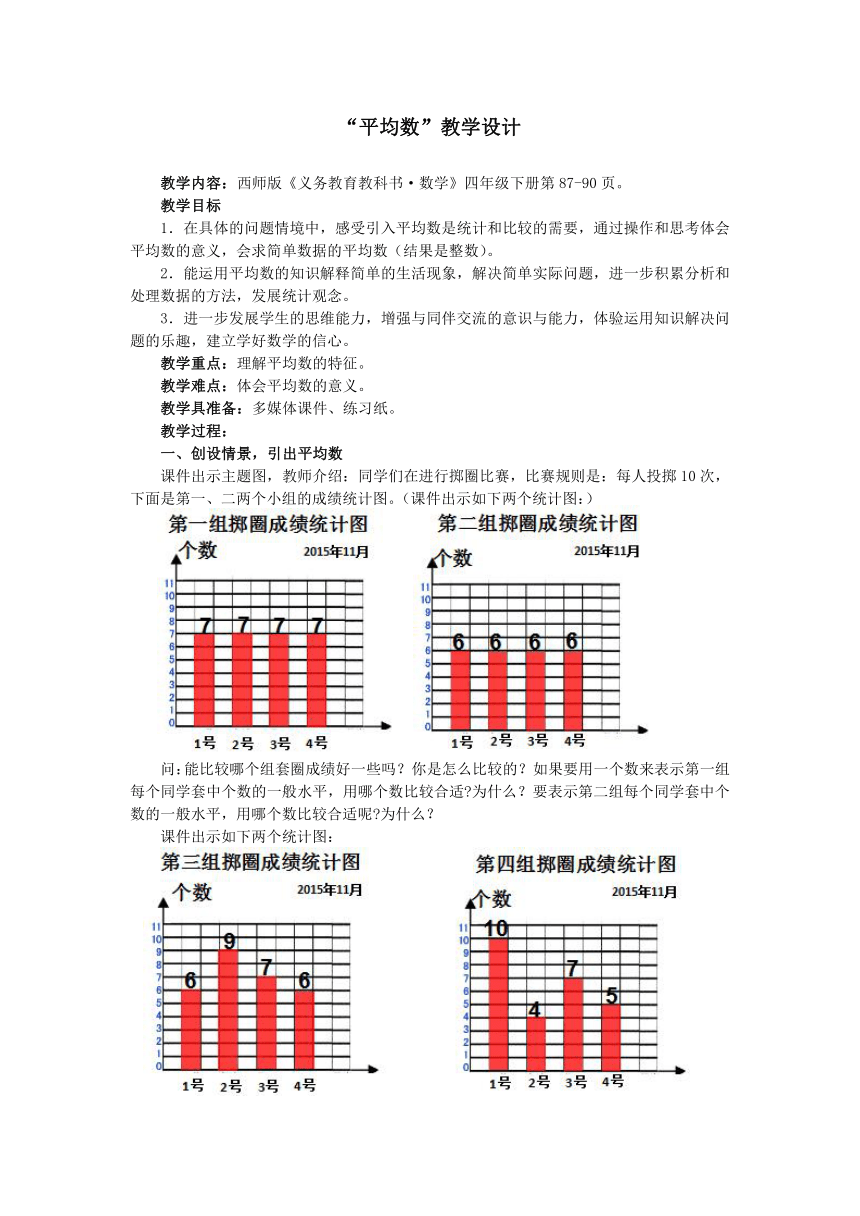
课件出示主题图,教师介绍:同学们在进行掷圈比赛,比赛规则是:每人投掷10次,下面是第一、二两个小组的成绩统计图。(课件出示如下两个统计图:)
问:能比较哪个组套圈成绩好一些吗?你是怎么比较的?如果要用一个数来表示第一组每个同学套中个数的一般水平,用哪个数比较合适?为什么?要表示第二组每个同学套中个数的一般水平,用哪个数比较合适呢?为什么?
课件出示如下两个统计图:
问:你认为这两个组哪一个组的成绩好一些?为什么?你是怎么比较的?
(预设:分别求出每个组投中个数的和,再比较。)
课件出示如下两个统计图:
问:还能用求和的方法比较这两个组的掷圈成绩吗?为什么?用什么数来比较这两个组的成绩最合适?(预设:7〉6,用代表一般水平的那个数比较最合适)。
课件出示如下两个统计图:
问:比较这两个组的套圈成绩,显然也不能用求和的方法来比较,你认为怎么比较呢?
(预设:要是有一个能分别代表第7组或第8组套圈成绩一般水平的数就能比较了。)
揭示课题:代表一组数据一般水平的那个数就是这组数据的平均数,这节课我们就一起学习平均数(板书:平均数)
【设计意图:通过上述具体的问题情境,让学生感受引入平均数是统计和比较的需要。同时也孕伏了平均数的特征之一—代表一组数据的一般特征。】
二、讨论探索,理解平均数
1.直观操作,移多补少。
我们先来看第七组套中个数的情况(课件出示)套得最多的和套得最少的能代表这个组每个同学套中个数的一般水平吗?那么表示这个组每个同学套中个数的一般水平的平均数应该在什么范围呢?
课件演示:通过移多补少,得出每人都同样多。通过移动后得到的平均数画上虚线,直观感知平均数的范围。
提问:得到的平均数“7”表示什么含义?你觉得平均数是一个怎样的数?这个平均数“7”与3号同学套中的个数“7”有什么不一样?
抽象思考,列式计算。
问:除了用在统计图上移动小方格的方法求出平均数,还可以怎样算出平均数呢?(先独立思考,然后小组交流,再全班交流)
交流后板书:6+9+7+6=28(个),28÷4=7(个)。
课件动态演示:把6个、9个、7个、6个小方格合并起来,再平均分成4份。
小结:用移多补少与求和均分的方法都能求出平均数,请你任选一种方法求出第八组平均每人套中多少个?
课件出示第八组套圈成绩统计图。
交流后板书:10+4+7+5+4=30(个),30÷5=6(个)
问:那么,现在可以比较出第七、八组哪个组的成绩好一些吗?
提问小结:在人数不相等的情况下,用平均数能比较出两个组的套圈成绩。通过刚才求出两个平均数并进行比较套圈情况,你觉得平均数是一个什么样的数?(预设:在最大数和最小数之间,代表一组数据的一般水平)
3.体会多出平均数的部分与少于平均数的部分相等。
问:以第7组的统计图为例(课件出示下图)。仔细观察,有没有发现这里有些数超过了平均数,而有些数还不到平均数?比较一下超过的部分与不到的部分,你发现了什么?(预设:超过的部分和不到的部分一样多,都是2个。)
?? 问:会不会只是一种巧合呢?让我们再来看看第八组的统计图吧?让学生观察片刻(预设:也是这样的。)
??追问:奇怪,为什么每一幅图中,超出平均数的部分和不到平均数的部分都一样多呢?
(预设:如果不一样多,超过的部分移下来后,就不可能把不到的部分正好填满。这样就得不到平均数了。)
??小结:是的!其实,像这样超出平均数的部分和不到平均数的部分一样多,这是平均数的又一个重要特点。把握了这一特点,我们可以巧妙地解决相关的实际问题。课件出示:
1.小红、小兰、小丽和小明他们4人小组一周收集塑料瓶的情况如下:小红14个,小兰12个,小丽11个,小明15个。哪个数能代表这一组每人收集塑料瓶个数的一般水平呢?
我们不计算,看看哪个数是这一组数据的平均数?(课件依次移动表示平均数的虚线11、12、13、14,学生判断,师适时追问为什么不是或者是)
2.师课件出示三根彩带:
问:老师大概估计了一下,觉得这三根彩带的平均长度大约是16厘米。不计算,你能根据平均数的特点,大概地判断一下,老师的这一估计对吗?
(预设:我觉得不对。因为黄色彩带比蓝色彩带长了8厘米,而红色彩带比蓝色彩带才短2厘米,不相等。所以,它们的平均长度不可能是16厘米。)
追问:照你看来,它们的平均长度会比16厘米长还是短?
师:它们的平均长度到底是多少?还是赶紧口算一下吧!
【设计意图:本环节旨在让学生感受平均数的特征:代表一组数据的一般特征;处在一组数据中最大数和最小数之间,在一组数据中超出平均数的部分等于低于平均数的部分;它是出于比较的需要而虚拟的一个数。也让学生学会求平均数的两种方法:移多补少,求和均分。】
??三、解释应用,巩固平均数
1.解读平均水深。
课件出示情境图:
问:陈宁来到一个池塘边。低头一看,发现了什么?(平均水深110厘米。)
?? 问:陈宁心想,这也太浅了,我的身高是120厘米,下水洗澡一定没危险。你们觉得不会游泳的陈宁这样想对吗?(预设:不对!)
?? 追问:怎么不对?陈宁的身高不是已经超过平均水深了吗?(预设:平均水深110厘米,并不是说池塘里每一处水深都是110厘米。可能有的地方比较浅,只有几十厘米,而有的地方比较深,比如150厘米。所以,陈宁下水游泳可能会有危险。)
师评价:说得真好!想看看这个池塘水底下的真实情形吗?
课件出示池塘水底的剖面图:
(预设:啊!原来是这样,真的有危险!)
??小结:看来,认识了平均数,对于我们解决生活中的问题还真有不少帮助呢。下面我们再来解决几个生活中的数学问题。请拿出练习纸,完成上面的题。
2.课堂作业。
学生独立解决下面三个数学问题:(打印在练习纸上)
在一次数学单元考试中,第9组和第10组的成绩如下,根据下面两组数据,比较第9组、第10组的成绩哪个组更好?
第9组中每人的分数如下:100、94、84、86。
第10组中每人的分数如下:100、85、97、90、78。
第6次全国人口普查显示,2010年我国平均每户人口数为3.1人。关于对“平均每户人口数为3.1人”的说法正确的是( )
A.这是不可能的,人数不可能为小数。
B.可能是统计错了或者是计算错了,才得出这么一个错误的数据。
C.这是一个虚拟的数,并不表示某个家庭的实际人数,但能代表我国每户人口数的一般水平,具有典型性。
某学校校园十佳小歌手歌唱比赛中某选手的得分情况如下:
评委 1 2 3 4 5 平均分
得分 92 98 95 53 92 ?
【 设计意图:本环节既有解释生活中的平均数,又有应用平均数解决问题,旨在进一步感受平均数的应用价值,培养学生的应用意识,并渗透安全教育。】
4.体会极端数据对平均数的影响。
第③题你们算出的平均分是多少分?(86分)可是记分员算出的平均分数是93分,知道这是怎么回事吗?(预设:去掉了一个最高分和一个最低分,再算的剩下3个分数的平均分。)
谈话:在歌咏比赛中,评委打分后,为什么要去掉一个最高分和一个最低分,再求剩下几个分数的平均数作为选手的成绩呢?让我们先来看看下面这个例子。
课件出示:有一位老师带着一群孩子在做游戏,他们的平均年龄是11岁,请你们猜猜这群孩子是小学生呢?还是幼儿园的孩子?(预设:小学生)
学生猜后出示答案:53岁、3岁、3岁、4岁、4岁、5岁、5岁。
师:是什么原因导致你们猜错了?(53这个数)是啊,53岁相比于其他年龄数来说太大了。我们把一组数据中特别大或者特别小的数称为这组数据的极端数。从这个例子可以看出:一组数据中有极端数的话,平均数就有可能失灵。
问:现在你明白计分员给参赛选手计分时为什么要去掉一个最高分和一个最低分了吧?
小结:是的,为了避免极端数据对平均数的影响,所以计分员在评委打分后,往往要去掉一个最高分和一个最低分,再求剩下几个分数的平均数作为选手的成绩。
【设计意图:让学生在猜一猜的过程中充分体验极端数对平均数的影响,对“去掉一个最高分和一个最低分然后再求剩下分数的平均数作为参赛选手的成绩的做法”理解深刻。】
四、总结全课,拓展延伸
问:通过这节课的学习,你知道平均数到底是一个怎样的数?怎样求一个数的平均数?
问:其实,上面那一组年龄数,用平均数不能代表它们的一般水平,人们又引进中位数或者众数来代表它们的一般特征。那么,什么是中位数?什么是众数呢?请同学们课后上网查一查吧!
【设计意图:通过对平均数特征和求平均数方法的总结,提高学生的认识,提升学生的技能。让学生带着问题走进课堂,也让学生带着问题离开教室,达到课虽终,思未尽的境界。】
教学内容:西师版《义务教育教科书·数学》四年级下册第87-90页。
教学目标
1.在具体的问题情境中,感受引入平均数是统计和比较的需要,通过操作和思考体会平均数的意义,会求简单数据的平均数(结果是整数)。
2.能运用平均数的知识解释简单的生活现象,解决简单实际问题,进一步积累分析和处理数据的方法,发展统计观念。
3.进一步发展学生的思维能力,增强与同伴交流的意识与能力,体验运用知识解决问题的乐趣,建立学好数学的信心。
教学重点:理解平均数的特征。
教学难点:体会平均数的意义。
教学具准备:多媒体课件、练习纸。
教学过程:
一、创设情景,引出平均数
课件出示主题图,教师介绍:同学们在进行掷圈比赛,比赛规则是:每人投掷10次,下面是第一、二两个小组的成绩统计图。(课件出示如下两个统计图:)
问:能比较哪个组套圈成绩好一些吗?你是怎么比较的?如果要用一个数来表示第一组每个同学套中个数的一般水平,用哪个数比较合适?为什么?要表示第二组每个同学套中个数的一般水平,用哪个数比较合适呢?为什么?
课件出示如下两个统计图:
问:你认为这两个组哪一个组的成绩好一些?为什么?你是怎么比较的?
(预设:分别求出每个组投中个数的和,再比较。)
课件出示如下两个统计图:
问:还能用求和的方法比较这两个组的掷圈成绩吗?为什么?用什么数来比较这两个组的成绩最合适?(预设:7〉6,用代表一般水平的那个数比较最合适)。
课件出示如下两个统计图:
问:比较这两个组的套圈成绩,显然也不能用求和的方法来比较,你认为怎么比较呢?
(预设:要是有一个能分别代表第7组或第8组套圈成绩一般水平的数就能比较了。)
揭示课题:代表一组数据一般水平的那个数就是这组数据的平均数,这节课我们就一起学习平均数(板书:平均数)
【设计意图:通过上述具体的问题情境,让学生感受引入平均数是统计和比较的需要。同时也孕伏了平均数的特征之一—代表一组数据的一般特征。】
二、讨论探索,理解平均数
1.直观操作,移多补少。
我们先来看第七组套中个数的情况(课件出示)套得最多的和套得最少的能代表这个组每个同学套中个数的一般水平吗?那么表示这个组每个同学套中个数的一般水平的平均数应该在什么范围呢?
课件演示:通过移多补少,得出每人都同样多。通过移动后得到的平均数画上虚线,直观感知平均数的范围。
提问:得到的平均数“7”表示什么含义?你觉得平均数是一个怎样的数?这个平均数“7”与3号同学套中的个数“7”有什么不一样?
抽象思考,列式计算。
问:除了用在统计图上移动小方格的方法求出平均数,还可以怎样算出平均数呢?(先独立思考,然后小组交流,再全班交流)
交流后板书:6+9+7+6=28(个),28÷4=7(个)。
课件动态演示:把6个、9个、7个、6个小方格合并起来,再平均分成4份。
小结:用移多补少与求和均分的方法都能求出平均数,请你任选一种方法求出第八组平均每人套中多少个?
课件出示第八组套圈成绩统计图。
交流后板书:10+4+7+5+4=30(个),30÷5=6(个)
问:那么,现在可以比较出第七、八组哪个组的成绩好一些吗?
提问小结:在人数不相等的情况下,用平均数能比较出两个组的套圈成绩。通过刚才求出两个平均数并进行比较套圈情况,你觉得平均数是一个什么样的数?(预设:在最大数和最小数之间,代表一组数据的一般水平)
3.体会多出平均数的部分与少于平均数的部分相等。
问:以第7组的统计图为例(课件出示下图)。仔细观察,有没有发现这里有些数超过了平均数,而有些数还不到平均数?比较一下超过的部分与不到的部分,你发现了什么?(预设:超过的部分和不到的部分一样多,都是2个。)
?? 问:会不会只是一种巧合呢?让我们再来看看第八组的统计图吧?让学生观察片刻(预设:也是这样的。)
??追问:奇怪,为什么每一幅图中,超出平均数的部分和不到平均数的部分都一样多呢?
(预设:如果不一样多,超过的部分移下来后,就不可能把不到的部分正好填满。这样就得不到平均数了。)
??小结:是的!其实,像这样超出平均数的部分和不到平均数的部分一样多,这是平均数的又一个重要特点。把握了这一特点,我们可以巧妙地解决相关的实际问题。课件出示:
1.小红、小兰、小丽和小明他们4人小组一周收集塑料瓶的情况如下:小红14个,小兰12个,小丽11个,小明15个。哪个数能代表这一组每人收集塑料瓶个数的一般水平呢?
我们不计算,看看哪个数是这一组数据的平均数?(课件依次移动表示平均数的虚线11、12、13、14,学生判断,师适时追问为什么不是或者是)
2.师课件出示三根彩带:
问:老师大概估计了一下,觉得这三根彩带的平均长度大约是16厘米。不计算,你能根据平均数的特点,大概地判断一下,老师的这一估计对吗?
(预设:我觉得不对。因为黄色彩带比蓝色彩带长了8厘米,而红色彩带比蓝色彩带才短2厘米,不相等。所以,它们的平均长度不可能是16厘米。)
追问:照你看来,它们的平均长度会比16厘米长还是短?
师:它们的平均长度到底是多少?还是赶紧口算一下吧!
【设计意图:本环节旨在让学生感受平均数的特征:代表一组数据的一般特征;处在一组数据中最大数和最小数之间,在一组数据中超出平均数的部分等于低于平均数的部分;它是出于比较的需要而虚拟的一个数。也让学生学会求平均数的两种方法:移多补少,求和均分。】
??三、解释应用,巩固平均数
1.解读平均水深。
课件出示情境图:
问:陈宁来到一个池塘边。低头一看,发现了什么?(平均水深110厘米。)
?? 问:陈宁心想,这也太浅了,我的身高是120厘米,下水洗澡一定没危险。你们觉得不会游泳的陈宁这样想对吗?(预设:不对!)
?? 追问:怎么不对?陈宁的身高不是已经超过平均水深了吗?(预设:平均水深110厘米,并不是说池塘里每一处水深都是110厘米。可能有的地方比较浅,只有几十厘米,而有的地方比较深,比如150厘米。所以,陈宁下水游泳可能会有危险。)
师评价:说得真好!想看看这个池塘水底下的真实情形吗?
课件出示池塘水底的剖面图:
(预设:啊!原来是这样,真的有危险!)
??小结:看来,认识了平均数,对于我们解决生活中的问题还真有不少帮助呢。下面我们再来解决几个生活中的数学问题。请拿出练习纸,完成上面的题。
2.课堂作业。
学生独立解决下面三个数学问题:(打印在练习纸上)
在一次数学单元考试中,第9组和第10组的成绩如下,根据下面两组数据,比较第9组、第10组的成绩哪个组更好?
第9组中每人的分数如下:100、94、84、86。
第10组中每人的分数如下:100、85、97、90、78。
第6次全国人口普查显示,2010年我国平均每户人口数为3.1人。关于对“平均每户人口数为3.1人”的说法正确的是( )
A.这是不可能的,人数不可能为小数。
B.可能是统计错了或者是计算错了,才得出这么一个错误的数据。
C.这是一个虚拟的数,并不表示某个家庭的实际人数,但能代表我国每户人口数的一般水平,具有典型性。
某学校校园十佳小歌手歌唱比赛中某选手的得分情况如下:
评委 1 2 3 4 5 平均分
得分 92 98 95 53 92 ?
【 设计意图:本环节既有解释生活中的平均数,又有应用平均数解决问题,旨在进一步感受平均数的应用价值,培养学生的应用意识,并渗透安全教育。】
4.体会极端数据对平均数的影响。
第③题你们算出的平均分是多少分?(86分)可是记分员算出的平均分数是93分,知道这是怎么回事吗?(预设:去掉了一个最高分和一个最低分,再算的剩下3个分数的平均分。)
谈话:在歌咏比赛中,评委打分后,为什么要去掉一个最高分和一个最低分,再求剩下几个分数的平均数作为选手的成绩呢?让我们先来看看下面这个例子。
课件出示:有一位老师带着一群孩子在做游戏,他们的平均年龄是11岁,请你们猜猜这群孩子是小学生呢?还是幼儿园的孩子?(预设:小学生)
学生猜后出示答案:53岁、3岁、3岁、4岁、4岁、5岁、5岁。
师:是什么原因导致你们猜错了?(53这个数)是啊,53岁相比于其他年龄数来说太大了。我们把一组数据中特别大或者特别小的数称为这组数据的极端数。从这个例子可以看出:一组数据中有极端数的话,平均数就有可能失灵。
问:现在你明白计分员给参赛选手计分时为什么要去掉一个最高分和一个最低分了吧?
小结:是的,为了避免极端数据对平均数的影响,所以计分员在评委打分后,往往要去掉一个最高分和一个最低分,再求剩下几个分数的平均数作为选手的成绩。
【设计意图:让学生在猜一猜的过程中充分体验极端数对平均数的影响,对“去掉一个最高分和一个最低分然后再求剩下分数的平均数作为参赛选手的成绩的做法”理解深刻。】
四、总结全课,拓展延伸
问:通过这节课的学习,你知道平均数到底是一个怎样的数?怎样求一个数的平均数?
问:其实,上面那一组年龄数,用平均数不能代表它们的一般水平,人们又引进中位数或者众数来代表它们的一般特征。那么,什么是中位数?什么是众数呢?请同学们课后上网查一查吧!
【设计意图:通过对平均数特征和求平均数方法的总结,提高学生的认识,提升学生的技能。让学生带着问题走进课堂,也让学生带着问题离开教室,达到课虽终,思未尽的境界。】
