上海市实验高级中学校2020-2021学年高二下学期3月第4周周测数学试题 Word版含答案
文档属性
| 名称 | 上海市实验高级中学校2020-2021学年高二下学期3月第4周周测数学试题 Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 754.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 00:00:00 | ||
图片预览




文档简介
上海市实验学校高二数学周测试卷
一、判断题(每小题2分,共20分)
1.在本大题中,false是三条互不重合的直线,false是三个互不重合的平面.
(1)若false,false,则false; (2)若false,false,则false;
(3)若false,false,则false; (4)若false,false,则false;
(5)若false,false,则false; (6)若false,false,则false;
(7)若false,false,则false; (8)若false,false,则false;
(9)若false,false,false,则false;
(10)若false,false,false,则false.
二、填空题(每小题3分,共24分)
2.空间四边形ABCD中,E、F、G、H依次为AB、BC、CD、DA边的中点,且AC=2,BD=4,则false= .
3.对于已知直线a,如果直线b同时满足下列三个条件:①与a是异面直线;②与a所成的角为定值;③与a的距离为定值. 那么,这样的直线有 条.
3714750186690M
D
C
B
A
P
M
D
C
B
A
P
4.在长方体false中,若false,则false与平面false所成的角false可用反三角函数值表示为false____________.
5.如图,在四棱锥false中,底面false是边长为false的
菱形,false,false平面false,false与平面false
所成角的大小为false,false为false的中点.则异面直线false
与false所成角的大小为 .
37014152330456.在菱形false中,false,false.false为菱形false所在平面false外的一点,false,false. false到直线false的距离为 .
7.如图,在棱长为2的正方体false中,E是
BC1的中点.则直线DE与平面ABCD所成角的大小为 .
8.ABCD为菱形,∠DAB=60°,PD⊥面ABCD,且PD=AD,则面PAB与面PCD所成的锐二面角的大小为 .
9.ABCD—A1B1C1D1是一个边长为1的正方体,过顶点A作正方体的截面(该截面与正方体的表面不重合),若截面的形状为四边形,则截面面积的取值范围是 .
三、选择题(每小题3分,共12分)
10. “直线垂直于的边,”是“直线垂直于的边”的( )
(A)充要条件 (B)充分非必要条件
(C)必要非充分条件 (D)即非充分也非必要条件
11. 设a,b,c表示三条直线,false表示两个平面,下列命题中不正确的是( )
A. falsefalse B. false
C. false D. false
12.如图,false为正方体false的中心,△false在该正方体各个面上的射影可能是( )
A. (1)、(2)、(3)、(4) B.(1)、(3) C.(1)、(4) D.(2)、(4)
13.已知棱长为1的正方体false中,点false,false分别是棱false,false上的动点,且falsefalse.设false与false所成的角为false,与false所成的角为false,则false的最小值( )
(A)不存在 (B)等于60 (C)等于90 (D)等于120
四、解答题
14.(本题满分false分)如图,直线false不在平面false上,直线false在false上,且false.试用反证法证明:false.
38950909525 证明:用反证法,若false,则false.
因为false,所以直线false确定一个平面false.
由于直线false在false上,所以false________.
因为false,且______________,所以false.
又因为false,故false,即false且false,
这样与已知中_______________矛盾,
所以false.
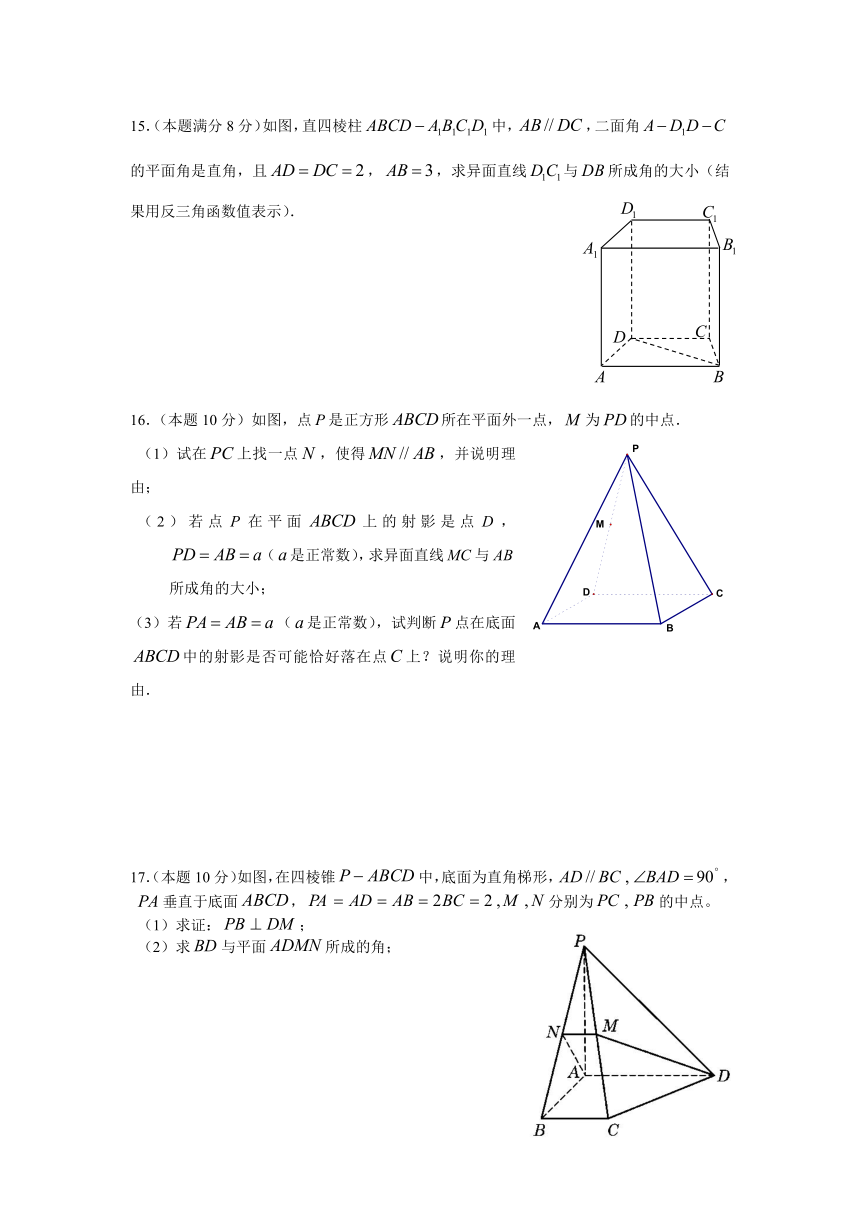
395097081407015.(本题满分8分)如图,直四棱柱false中,false,二面角false的平面角是直角,且false,false,求异面直线false与false所成角的大小(结果用反三角函数值表示).
16.(本题10分)如图,点false是正方形false所在平面外一点,false为false的中点.
35052005715(1)试在false上找一点false,使得false,并说明理由;
(2)若点false在平面false上的射影是点false,false(false是正常数),求异面直线false与false所成角的大小;
(3)若false(false是正常数),试判断false点在底面false中的射影是否可能恰好落在点false上?说明你的理由.
347662556261017.(本题10分)如图,在四棱锥中,底面为直角梯形,,垂直于底面,分别为的中点。
(1)求证:;
(2)求与平面所成的角;
18.(本题10分)如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=a(0<≦1).
(Ⅰ)求证:对任意的(0、1),都有AC⊥BE:
310261010795(Ⅱ)若二面角C-AE-D的大小为600C,求的值。
五、附加题
19.已知直三棱柱false中,false,false,false为false的中点。
(Ⅰ)求异面直线false和false的距离;
(Ⅱ)若false,求二面角false的平面角的余弦值。
347789510795
20.从O点引三条射线OA,OB, OC,其两两之间的夹角分别为false ,则这三个角的角平分线两两之间的夹角的最小值是多少?
上海市实验学校高二数学周测试卷解答
一、判断题(每小题2分,共20分)
1.在本大题中,false是三条互不重合的直线,false是三个互不重合的平面.
(1)若false,false,则false; (2)若false,false,则false;
(3)若false,false,则false; (4)若false,false,则false;
(5)若false,false,则false; (6)若false,false,则false;
(7)若false,false,则false; (8)若false,false,则false;
(9)若false,false,false,则false;
(10)若false,false,false,则false.
题号
1
2
3
4
5
6
7
8
9
10
答案
√
×
×
√
×
√
×
×
√
×
二、填空题(每小题3分,共24分)
2.空间四边形ABCD中,E、F、G、H依次为AB、BC、CD、DA边的中点,且AC=2,BD=4,则false= . 10
3.对于已知直线a,如果直线b同时满足下列三个条件:①与a是异面直线;②与a所成的角为定值;③与a的距离为定值. 那么,这样的直线有 条. 无数条
4.在长方体false中,若false,则false与平面false所成的角false可用反三角函数值表示为false____________.
答案:false
38100002540M
D
C
B
A
P
O
M
D
C
B
A
P
O
5.如图,在四棱锥false中,底面false是边长为false的
菱形,false,false平面false,false与平面false
所成角的大小为false,false为false的中点.则异面直线false
与false所成角的大小为 .
解:连结false,交false于点false,连结false,
因为false、false分别为false、false的中点,所以false∥false,
所以false(或其补角)为异面直线false与false所成的角.
在△false中,false,false,false
(以下由余弦定理,或说明△false是直角三角形求得)
false或false或false.
所以,异面直线false与false所成角的大小为false
6.在菱形false中,false,false.false为菱形false所在平面false外的一点,false,false. false到直线false的距离为 .5
33718505505457.如图,在棱长为2的正方体false中,E是BC1的中点.则直线DE与平面ABCD所成角的大小为 .
解:过E作EF⊥BC,交BC于F,连接DF.
∵ EF⊥平面ABCD,
∴ ∠EDF是直线DE与平面ABCD所成的角.
由题意,得EF=false
∵ false
∵ EF⊥DF, ∴ false
故直线DE与平面ABCD所成角的大小是false
8.ABCD为菱形,∠DAB=60°,PD⊥面ABCD,且PD=AD,则面PAB与面PCD所成的锐二面角的大小为 . false
9.ABCD—A1B1C1D1是一个边长为1的正方体,过顶点A作正方体的截面(该截面与正方体的表面不重合),若截面的形状为四边形,则截面面积的取值范围是 .
答案:false
三、选择题(每小题3分,共12分)
10. “直线垂直于的边,”是“直线垂直于的边”的( B ).
(A)充要条件 (B)充分非必要条件
(C)必要非充分条件 (D)即非充分也非必要条件
11. 设a,b,c表示三条直线,false表示两个平面,下列命题中不正确的是( D )
A. falsefalse B. false
C. false D. false
12.如图,false为正方体false的中心,△false在该正方体各个面上的射影可能是( C )
A. (1)、(2)、(3)、(4) B.(1)、(3) C.(1)、(4) D.(2)、(4)
13.已知棱长为1的正方体false中,点false,false分别是棱false,false上的动点,且falsefalse.设false与false所成的角为false,与false所成的角为false,则false的最小值( C )
(A)不存在 (B)等于60 (C)等于90 (D)等于120
三、解答题
14.(本题满分false分)如图,直线false不在平面false上,直线false在false上,且false.试用反证法证明:false.
38950909525 证明:用反证法,若false,则false.
因为false,所以直线false确定一个平面false.
由于直线false在false上,所以false___b___.
因为false,且_____falsefalsefalse_____,所以false.
又因为false,故false,即false且false,
这样与已知中_____false_____矛盾,
所以false.
395097081407015.(本题满分8分)如图,直四棱柱false中,false,二面角false的平面角是直角,且false,false,求异面直线false与false所成角的大小(结果用反三角函数值表示).
解:false直四棱柱false中,false,
∴false的大小即为异面直线false与false所成的角的大小,
又false直四棱柱false中,侧棱false面false,
∴false,false,
∴false即为二面角false的平面角,∴false.
在false中, false,false
∴ false
∴false,即异面直线false与false所成的角的大小为false.
16.(本题10分)如图,点false是正方形false所在平面外一点,false为false的中点.
35052005715(1)试在false上找一点false,使得false,并说明理由;
(2)若点false在平面false上的射影是点false,false(false是正常数),求异面直线false与false所成角的大小;
(3)若false(false是正常数),试判断false点在底面false中的射影是否可能恰好落在点false上?说明你的理由.
解:(1)false为false的中点.
在平面false中,过false作false,
又因为false,所以 false.
(2)因为false,所以false为异面直线false与false所成角.
因为点false在平面上的射影是点false,所以在直角false中,false.
即异面直线false与false所成角的大小为false.
(3)不可能.
若false点在底面false中的射影是否可能恰好落在点false上,即false平面false.
又因为正方形false的边长为false,则对角线false,
在直角false中,false,矛盾!
17.(本题10分)如图,在四棱锥中,底面为直角梯形,,垂直于底面,分别为的中点。
(1)求证:;(2)求与平面所成的角;
解:(1)证明:因为是的中点,, 所以。
375729578105由底面,得,
又,即,
平面,所以 ,
平面, 。
(2)连结,
因为平面,即平面,
所以是与平面所成的角,
在中,,
在中,,
故,
在中, ,
又,故与平面所成的角是。
136004503962408.(本题10分)如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=a(0<≦1).
(Ⅰ)求证:对任意的(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C,求的值。
解:(Ⅰ)证:连接BD,由底面是正方形可得ACBD。
SD平面ABCD,BD是BE在平面ABCD上的射影,由三垂线定理得ACBE.
(II)解:SD平面ABCD,CD平面ABCD, SDCD.
又底面ABCD是正方形, CDAD,又SDAD=D,CD平面SAD。
过点D在平面SAD内做DFAE于F,连接CF,则CFAE,
故CFD是二面角C-AE-D 的平面角,即CFD=60°
在Rt△ADE中,AD=, DE= , AE= 。
323850078105于是,DF=
在Rt△CDF中,由cot60°=
得,
即=3 , 解得=
四、附加题
19.已知直三棱柱false中,false,false,false为false的中点。
(Ⅰ)求异面直线false和false的距离;
(Ⅱ)若false,求二面角false的平面角的余弦值。
解:(Ⅰ)如图,因AC=BC, D为AB的中点,
故CD falseAB。又直三棱柱中,false 面false ,
故false,
所以异面直线false 和AB的距离为:
353250576200false
(Ⅱ):由false故false 面false ,
从而false,false
故false 为所求的二面角false的平面角。
因false是false在面false上的射影,又已知false
由三垂线定理的逆定理得false
从而false,false都与false互余,
因此false,
所以false≌false,因此false
得false
从而false
所以在false中,
由余弦定理得false
363347027305020.从O点引三条射线OA,OB, OC,其两两之间的夹角分别为false ,则这三个角的角平分线两两之间的夹角的最小值是多少?
解:如图,不妨设OA与OB的夹角为false,OB与OC的夹角为false,OC与OA的夹角为false,在OA,OB, OC上分别取点false,使得false
作∠AOB,∠BOC,∠COA的角平分线分别交 false于D,E,F,
则false,且D,E,F分别是
false的中点.
正△false中,false,等腰Rt△false中,false,
△false中,false,
又false
且false
所以false
所以false
所以这三个角的角平分线两两之间的夹角的最小值是false
一、判断题(每小题2分,共20分)
1.在本大题中,false是三条互不重合的直线,false是三个互不重合的平面.
(1)若false,false,则false; (2)若false,false,则false;
(3)若false,false,则false; (4)若false,false,则false;
(5)若false,false,则false; (6)若false,false,则false;
(7)若false,false,则false; (8)若false,false,则false;
(9)若false,false,false,则false;
(10)若false,false,false,则false.
二、填空题(每小题3分,共24分)
2.空间四边形ABCD中,E、F、G、H依次为AB、BC、CD、DA边的中点,且AC=2,BD=4,则false= .
3.对于已知直线a,如果直线b同时满足下列三个条件:①与a是异面直线;②与a所成的角为定值;③与a的距离为定值. 那么,这样的直线有 条.
3714750186690M
D
C
B
A
P
M
D
C
B
A
P
4.在长方体false中,若false,则false与平面false所成的角false可用反三角函数值表示为false____________.
5.如图,在四棱锥false中,底面false是边长为false的
菱形,false,false平面false,false与平面false
所成角的大小为false,false为false的中点.则异面直线false
与false所成角的大小为 .
37014152330456.在菱形false中,false,false.false为菱形false所在平面false外的一点,false,false. false到直线false的距离为 .
7.如图,在棱长为2的正方体false中,E是
BC1的中点.则直线DE与平面ABCD所成角的大小为 .
8.ABCD为菱形,∠DAB=60°,PD⊥面ABCD,且PD=AD,则面PAB与面PCD所成的锐二面角的大小为 .
9.ABCD—A1B1C1D1是一个边长为1的正方体,过顶点A作正方体的截面(该截面与正方体的表面不重合),若截面的形状为四边形,则截面面积的取值范围是 .
三、选择题(每小题3分,共12分)
10. “直线垂直于的边,”是“直线垂直于的边”的( )
(A)充要条件 (B)充分非必要条件
(C)必要非充分条件 (D)即非充分也非必要条件
11. 设a,b,c表示三条直线,false表示两个平面,下列命题中不正确的是( )
A. falsefalse B. false
C. false D. false
12.如图,false为正方体false的中心,△false在该正方体各个面上的射影可能是( )
A. (1)、(2)、(3)、(4) B.(1)、(3) C.(1)、(4) D.(2)、(4)
13.已知棱长为1的正方体false中,点false,false分别是棱false,false上的动点,且falsefalse.设false与false所成的角为false,与false所成的角为false,则false的最小值( )
(A)不存在 (B)等于60 (C)等于90 (D)等于120
四、解答题
14.(本题满分false分)如图,直线false不在平面false上,直线false在false上,且false.试用反证法证明:false.
38950909525 证明:用反证法,若false,则false.
因为false,所以直线false确定一个平面false.
由于直线false在false上,所以false________.
因为false,且______________,所以false.
又因为false,故false,即false且false,
这样与已知中_______________矛盾,
所以false.
395097081407015.(本题满分8分)如图,直四棱柱false中,false,二面角false的平面角是直角,且false,false,求异面直线false与false所成角的大小(结果用反三角函数值表示).
16.(本题10分)如图,点false是正方形false所在平面外一点,false为false的中点.
35052005715(1)试在false上找一点false,使得false,并说明理由;
(2)若点false在平面false上的射影是点false,false(false是正常数),求异面直线false与false所成角的大小;
(3)若false(false是正常数),试判断false点在底面false中的射影是否可能恰好落在点false上?说明你的理由.
347662556261017.(本题10分)如图,在四棱锥中,底面为直角梯形,,垂直于底面,分别为的中点。
(1)求证:;
(2)求与平面所成的角;
18.(本题10分)如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=a(0<≦1).
(Ⅰ)求证:对任意的(0、1),都有AC⊥BE:
310261010795(Ⅱ)若二面角C-AE-D的大小为600C,求的值。
五、附加题
19.已知直三棱柱false中,false,false,false为false的中点。
(Ⅰ)求异面直线false和false的距离;
(Ⅱ)若false,求二面角false的平面角的余弦值。
347789510795
20.从O点引三条射线OA,OB, OC,其两两之间的夹角分别为false ,则这三个角的角平分线两两之间的夹角的最小值是多少?
上海市实验学校高二数学周测试卷解答
一、判断题(每小题2分,共20分)
1.在本大题中,false是三条互不重合的直线,false是三个互不重合的平面.
(1)若false,false,则false; (2)若false,false,则false;
(3)若false,false,则false; (4)若false,false,则false;
(5)若false,false,则false; (6)若false,false,则false;
(7)若false,false,则false; (8)若false,false,则false;
(9)若false,false,false,则false;
(10)若false,false,false,则false.
题号
1
2
3
4
5
6
7
8
9
10
答案
√
×
×
√
×
√
×
×
√
×
二、填空题(每小题3分,共24分)
2.空间四边形ABCD中,E、F、G、H依次为AB、BC、CD、DA边的中点,且AC=2,BD=4,则false= . 10
3.对于已知直线a,如果直线b同时满足下列三个条件:①与a是异面直线;②与a所成的角为定值;③与a的距离为定值. 那么,这样的直线有 条. 无数条
4.在长方体false中,若false,则false与平面false所成的角false可用反三角函数值表示为false____________.
答案:false
38100002540M
D
C
B
A
P
O
M
D
C
B
A
P
O
5.如图,在四棱锥false中,底面false是边长为false的
菱形,false,false平面false,false与平面false
所成角的大小为false,false为false的中点.则异面直线false
与false所成角的大小为 .
解:连结false,交false于点false,连结false,
因为false、false分别为false、false的中点,所以false∥false,
所以false(或其补角)为异面直线false与false所成的角.
在△false中,false,false,false
(以下由余弦定理,或说明△false是直角三角形求得)
false或false或false.
所以,异面直线false与false所成角的大小为false
6.在菱形false中,false,false.false为菱形false所在平面false外的一点,false,false. false到直线false的距离为 .5
33718505505457.如图,在棱长为2的正方体false中,E是BC1的中点.则直线DE与平面ABCD所成角的大小为 .
解:过E作EF⊥BC,交BC于F,连接DF.
∵ EF⊥平面ABCD,
∴ ∠EDF是直线DE与平面ABCD所成的角.
由题意,得EF=false
∵ false
∵ EF⊥DF, ∴ false
故直线DE与平面ABCD所成角的大小是false
8.ABCD为菱形,∠DAB=60°,PD⊥面ABCD,且PD=AD,则面PAB与面PCD所成的锐二面角的大小为 . false
9.ABCD—A1B1C1D1是一个边长为1的正方体,过顶点A作正方体的截面(该截面与正方体的表面不重合),若截面的形状为四边形,则截面面积的取值范围是 .
答案:false
三、选择题(每小题3分,共12分)
10. “直线垂直于的边,”是“直线垂直于的边”的( B ).
(A)充要条件 (B)充分非必要条件
(C)必要非充分条件 (D)即非充分也非必要条件
11. 设a,b,c表示三条直线,false表示两个平面,下列命题中不正确的是( D )
A. falsefalse B. false
C. false D. false
12.如图,false为正方体false的中心,△false在该正方体各个面上的射影可能是( C )
A. (1)、(2)、(3)、(4) B.(1)、(3) C.(1)、(4) D.(2)、(4)
13.已知棱长为1的正方体false中,点false,false分别是棱false,false上的动点,且falsefalse.设false与false所成的角为false,与false所成的角为false,则false的最小值( C )
(A)不存在 (B)等于60 (C)等于90 (D)等于120
三、解答题
14.(本题满分false分)如图,直线false不在平面false上,直线false在false上,且false.试用反证法证明:false.
38950909525 证明:用反证法,若false,则false.
因为false,所以直线false确定一个平面false.
由于直线false在false上,所以false___b___.
因为false,且_____falsefalsefalse_____,所以false.
又因为false,故false,即false且false,
这样与已知中_____false_____矛盾,
所以false.
395097081407015.(本题满分8分)如图,直四棱柱false中,false,二面角false的平面角是直角,且false,false,求异面直线false与false所成角的大小(结果用反三角函数值表示).
解:false直四棱柱false中,false,
∴false的大小即为异面直线false与false所成的角的大小,
又false直四棱柱false中,侧棱false面false,
∴false,false,
∴false即为二面角false的平面角,∴false.
在false中, false,false
∴ false
∴false,即异面直线false与false所成的角的大小为false.
16.(本题10分)如图,点false是正方形false所在平面外一点,false为false的中点.
35052005715(1)试在false上找一点false,使得false,并说明理由;
(2)若点false在平面false上的射影是点false,false(false是正常数),求异面直线false与false所成角的大小;
(3)若false(false是正常数),试判断false点在底面false中的射影是否可能恰好落在点false上?说明你的理由.
解:(1)false为false的中点.
在平面false中,过false作false,
又因为false,所以 false.
(2)因为false,所以false为异面直线false与false所成角.
因为点false在平面上的射影是点false,所以在直角false中,false.
即异面直线false与false所成角的大小为false.
(3)不可能.
若false点在底面false中的射影是否可能恰好落在点false上,即false平面false.
又因为正方形false的边长为false,则对角线false,
在直角false中,false,矛盾!
17.(本题10分)如图,在四棱锥中,底面为直角梯形,,垂直于底面,分别为的中点。
(1)求证:;(2)求与平面所成的角;
解:(1)证明:因为是的中点,, 所以。
375729578105由底面,得,
又,即,
平面,所以 ,
平面, 。
(2)连结,
因为平面,即平面,
所以是与平面所成的角,
在中,,
在中,,
故,
在中, ,
又,故与平面所成的角是。
136004503962408.(本题10分)如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=a(0<≦1).
(Ⅰ)求证:对任意的(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C,求的值。
解:(Ⅰ)证:连接BD,由底面是正方形可得ACBD。
SD平面ABCD,BD是BE在平面ABCD上的射影,由三垂线定理得ACBE.
(II)解:SD平面ABCD,CD平面ABCD, SDCD.
又底面ABCD是正方形, CDAD,又SDAD=D,CD平面SAD。
过点D在平面SAD内做DFAE于F,连接CF,则CFAE,
故CFD是二面角C-AE-D 的平面角,即CFD=60°
在Rt△ADE中,AD=, DE= , AE= 。
323850078105于是,DF=
在Rt△CDF中,由cot60°=
得,
即=3 , 解得=
四、附加题
19.已知直三棱柱false中,false,false,false为false的中点。
(Ⅰ)求异面直线false和false的距离;
(Ⅱ)若false,求二面角false的平面角的余弦值。
解:(Ⅰ)如图,因AC=BC, D为AB的中点,
故CD falseAB。又直三棱柱中,false 面false ,
故false,
所以异面直线false 和AB的距离为:
353250576200false
(Ⅱ):由false故false 面false ,
从而false,false
故false 为所求的二面角false的平面角。
因false是false在面false上的射影,又已知false
由三垂线定理的逆定理得false
从而false,false都与false互余,
因此false,
所以false≌false,因此false
得false
从而false
所以在false中,
由余弦定理得false
363347027305020.从O点引三条射线OA,OB, OC,其两两之间的夹角分别为false ,则这三个角的角平分线两两之间的夹角的最小值是多少?
解:如图,不妨设OA与OB的夹角为false,OB与OC的夹角为false,OC与OA的夹角为false,在OA,OB, OC上分别取点false,使得false
作∠AOB,∠BOC,∠COA的角平分线分别交 false于D,E,F,
则false,且D,E,F分别是
false的中点.
正△false中,false,等腰Rt△false中,false,
△false中,false,
又false
且false
所以false
所以false
所以这三个角的角平分线两两之间的夹角的最小值是false
同课章节目录
