2020-2021学年人教版八年级下册数学:17.1勾股定理1学案
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学:17.1勾股定理1学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 72.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 12:28:52 | ||
图片预览

文档简介
年级:八年级
科目:数学
执笔:
审核:八年级数学组
课题:勾股定理(1)
课型:新授
时间:
学习目标:1.在勾股定理的探索过程中发展推理能力,体会数形结合的思想。
2.培养在实际生活中发现问题总结规律的意识和能力。
3.介绍我国古代在勾股定理研究方面所取得的成就,激发学生的爱国热情。
学习重点:探索和证明勾股定理。
学习难点:用拼图的方法证明勾股定理。
学习过程:
(1)
自主学习:
1、
上网查询有关勾股定理的内容;
2、
每名同学准备4个全等的一般直角三角形;并准备几张网格纸。
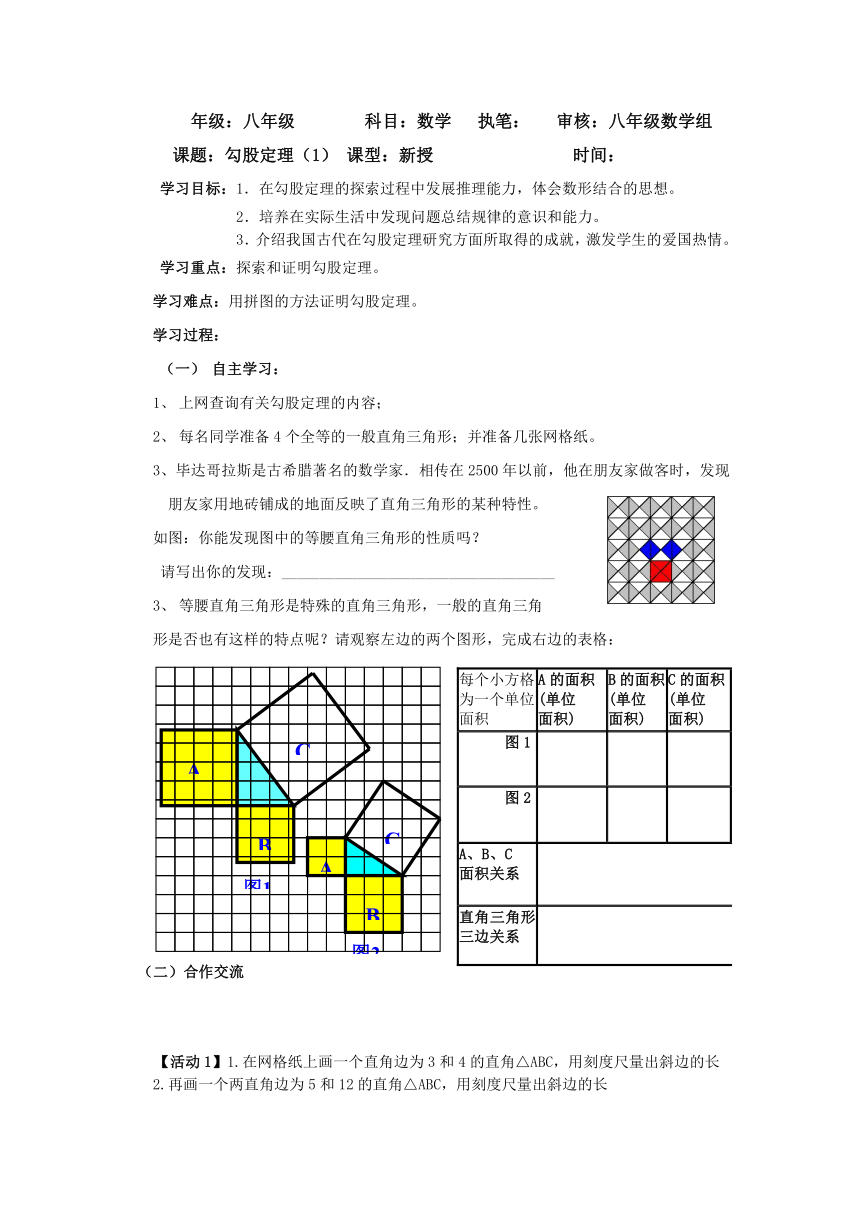
3、毕达哥拉斯是古希腊著名的数学家.相传在2500年以前,他在朋友家做客时,发现朋友家用地砖铺成的地面反映了直角三角形的某种特性。
如图:你能发现图中的等腰直角三角形的性质吗?
请写出你的发现:____________________________________
3、
等腰直角三角形是特殊的直角三角形,一般的直角三角
形是否也有这样的特点呢?请观察左边的两个图形,完成右边的表格:
每个小方格为一个单位面积
A的面积(单位面积)
B的面积(单位面积)
C的面积(单位面积)
图1
图2
A、B、C面积关系
直角三角形三边关系
(二)合作交流
【活动1】1.在网格纸上画一个直角边为3和4的直角△ABC,用刻度尺量出斜边的长
2.再画一个两直角边为5和12的直角△ABC,用刻度尺量出斜边的长
3.探究:你能发现其中斜边与两直角边之间的数量关系吗?写出你的结果:
________________________________________________________________
【活动2】猜想验证,小组实验:
猜想:直角三角形的两条直角边的平方和等于斜边的平方.
验证:以直角三角形ABC的两条直角边a,b为边做两个正方形。
方法一;如图,请同学们剪4个全等的直角三角形,拼成如图
图形,利用面积证明。
S正方形=_______________=____________________
化简得:__________________________
方法二;如图,请同学们剪4个全等的直角三角形,拼成如图图形,利用面积证明。
分析:左右两边的正方形边长相等,则两个正方形的面积
相等。左边S=______________右边S=_______________
左边和右边面积相等,
即
_____________________________________
化简可得_______________
方法三:如右图,可以利用两个全等的直角三角形拼出一
个梯形。借助这个图形,你能用面积法来验证勾股定理吗?
∵
RtΔEAD
≌
RtΔCBE,
∴
∠ADE
=
∠BEC.
∵
∠AED
+
∠ADE
=
90?,∴
∠AED
+
∠BEC
=
90?.
∴
∠DEC
=
180?―90?=
90?.
∴
ΔDEC是一个_____________三角形,它的面积等于_____________
∵四边形ABCD是一个直角梯形,∴
它的面积等于___________.
又∵S梯形=SΔ_______
+
SΔ________+
SΔ________.
∴
_____________=__________+__________+__________
化简得:________________.
勾股定理:如果直角三角形的两直角边长分别为,斜边长为,则_____________
(三)自我检测:
1、⑴在Rt△ABC,∠C=90°,a=3,b=4,则c=
。
⑵在Rt△ABC,∠B=90°,a=8,c=17,则b=
。
⑶在Rt△ABC,∠C=90°,a:b=3:4,c=10,则a=
,b=
。
⑷在Rt△ABC,∠C=90°,如果c=10,a-b=2,则b=
。
2、已知直角三角形的两直角边分别为5和12,则斜边长为
,斜边上的高为
3、已知直角三角形的两边长分别为3cm和5cm,,则第三边长为
。
4、下列各图中所示的线段的长度或正方形的面积为多少。
(注:下列各图中的三角形均为直角三角形)A=
y=
B=
教(学)后
感:_________________________________________________________
A
B
C
图1
A
B
C
图2
科目:数学
执笔:
审核:八年级数学组
课题:勾股定理(1)
课型:新授
时间:
学习目标:1.在勾股定理的探索过程中发展推理能力,体会数形结合的思想。
2.培养在实际生活中发现问题总结规律的意识和能力。
3.介绍我国古代在勾股定理研究方面所取得的成就,激发学生的爱国热情。
学习重点:探索和证明勾股定理。
学习难点:用拼图的方法证明勾股定理。
学习过程:
(1)
自主学习:
1、
上网查询有关勾股定理的内容;
2、
每名同学准备4个全等的一般直角三角形;并准备几张网格纸。
3、毕达哥拉斯是古希腊著名的数学家.相传在2500年以前,他在朋友家做客时,发现朋友家用地砖铺成的地面反映了直角三角形的某种特性。
如图:你能发现图中的等腰直角三角形的性质吗?
请写出你的发现:____________________________________
3、
等腰直角三角形是特殊的直角三角形,一般的直角三角
形是否也有这样的特点呢?请观察左边的两个图形,完成右边的表格:
每个小方格为一个单位面积
A的面积(单位面积)
B的面积(单位面积)
C的面积(单位面积)
图1
图2
A、B、C面积关系
直角三角形三边关系
(二)合作交流
【活动1】1.在网格纸上画一个直角边为3和4的直角△ABC,用刻度尺量出斜边的长
2.再画一个两直角边为5和12的直角△ABC,用刻度尺量出斜边的长
3.探究:你能发现其中斜边与两直角边之间的数量关系吗?写出你的结果:
________________________________________________________________
【活动2】猜想验证,小组实验:
猜想:直角三角形的两条直角边的平方和等于斜边的平方.
验证:以直角三角形ABC的两条直角边a,b为边做两个正方形。
方法一;如图,请同学们剪4个全等的直角三角形,拼成如图
图形,利用面积证明。
S正方形=_______________=____________________
化简得:__________________________
方法二;如图,请同学们剪4个全等的直角三角形,拼成如图图形,利用面积证明。
分析:左右两边的正方形边长相等,则两个正方形的面积
相等。左边S=______________右边S=_______________
左边和右边面积相等,
即
_____________________________________
化简可得_______________
方法三:如右图,可以利用两个全等的直角三角形拼出一
个梯形。借助这个图形,你能用面积法来验证勾股定理吗?
∵
RtΔEAD
≌
RtΔCBE,
∴
∠ADE
=
∠BEC.
∵
∠AED
+
∠ADE
=
90?,∴
∠AED
+
∠BEC
=
90?.
∴
∠DEC
=
180?―90?=
90?.
∴
ΔDEC是一个_____________三角形,它的面积等于_____________
∵四边形ABCD是一个直角梯形,∴
它的面积等于___________.
又∵S梯形=SΔ_______
+
SΔ________+
SΔ________.
∴
_____________=__________+__________+__________
化简得:________________.
勾股定理:如果直角三角形的两直角边长分别为,斜边长为,则_____________
(三)自我检测:
1、⑴在Rt△ABC,∠C=90°,a=3,b=4,则c=
。
⑵在Rt△ABC,∠B=90°,a=8,c=17,则b=
。
⑶在Rt△ABC,∠C=90°,a:b=3:4,c=10,则a=
,b=
。
⑷在Rt△ABC,∠C=90°,如果c=10,a-b=2,则b=
。
2、已知直角三角形的两直角边分别为5和12,则斜边长为
,斜边上的高为
3、已知直角三角形的两边长分别为3cm和5cm,,则第三边长为
。
4、下列各图中所示的线段的长度或正方形的面积为多少。
(注:下列各图中的三角形均为直角三角形)A=
y=
B=
教(学)后
感:_________________________________________________________
A
B
C
图1
A
B
C
图2
