2020-2021学年人教版八年级下册数学习题课件 第十七章 17.1 第1课时 勾股定理(共21张ppt)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学习题课件 第十七章 17.1 第1课时 勾股定理(共21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 466.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
人教版
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理
1.下列说法正确的是(
)
A.若a,b,c是△ABC的三边,则a2+b2=c2
B.若a,b,c是Rt△ABC的三边,则a2+b2=c2
C.若a,b,c是Rt△ABC的三边,∠A=90°,则a2+b2=c2
D.若a,b,c是Rt△ABC的三边,∠C=90°,则a2+b2=c2
D
2.利用如图(1)或(2)所示的两个图形中的有关面积的等量关系
都能证明数学中一个十分著名的定理,这个定理称为___________,
该定理中结论的数学解析式是_____________.
勾股定理
a2+b2=c2
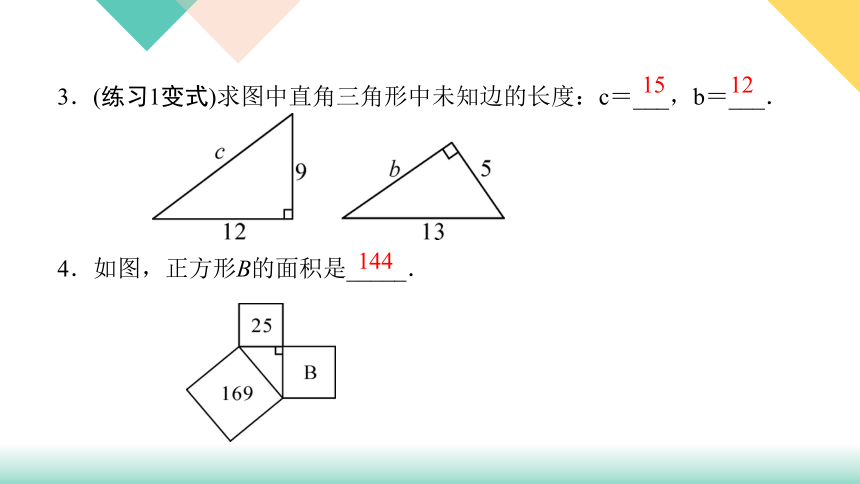
3.(练习1变式)求图中直角三角形中未知边的长度:c=___,b=___.
4.如图,正方形B的面积是_____.
15
12
144
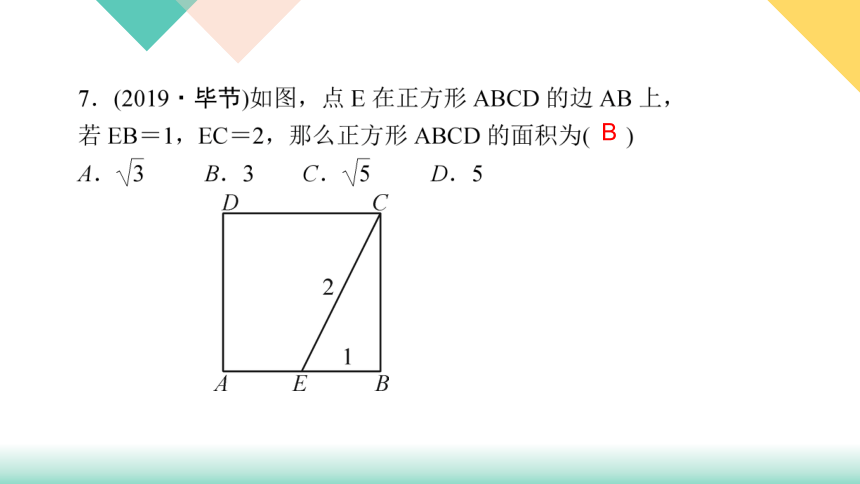
8
B
B
8.(习题1变式)在△ABC中,∠C=90°,
∠A,∠B,∠C的对边分别是a,b,c.
(1)若b=2,c=3,求a的值;
(2)若a∶c=3∶5,b=28,求a,c的值.
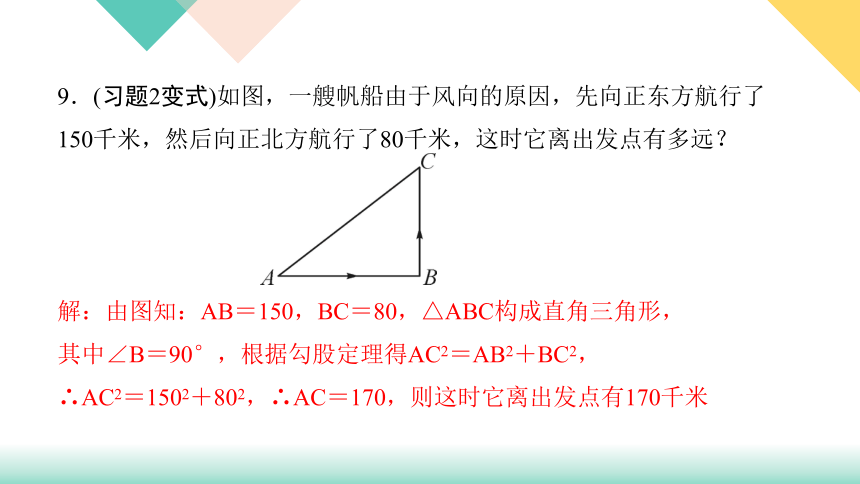
9.(习题2变式)如图,一艘帆船由于风向的原因,先向正东方航行了
150千米,然后向正北方航行了80千米,这时它离出发点有多远?
解:由图知:AB=150,BC=80,△ABC构成直角三角形,
其中∠B=90°,根据勾股定理得AC2=AB2+BC2,
∴AC2=1502+802,∴AC=170,则这时它离出发点有170千米
10.如图,直线l同侧有三个正方形a,b,c,
若a,c的面积分别为5和11,则b的面积为(
)
A.4
B.6
C.16
D.55
C
A
12.(练习2变式)如图,图中所有的四边形都是正方形,
所有的三角形都是直角三角形,其中最大的正方形E的边长为7
cm,
则正方形A,B,C,D的面积之和是________.
49
cm2
13.(2019·通辽)腰长为5,高为4的等腰三角形的底边长为_____________.
14.(1)(原创题)如图,在四边形ABCD中,AB=3,BC=4,AD=13,
BC⊥AB,对角线AC⊥CD,求CD的长;
(2)如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,
求AB的长.
15.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,
其中的“面积法”给了小聪以灵感,他惊喜的发现,
当两个全等的直角三角形如图①或图②摆放时,
都可以用“面积法”来证明,下面是小聪利用图①证明勾股定理的过程:
将两个全等的直角三角形按图①所示摆放,
其中∠DAB=90°,求证:a2+b2=c2.
人教版
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理
1.下列说法正确的是(
)
A.若a,b,c是△ABC的三边,则a2+b2=c2
B.若a,b,c是Rt△ABC的三边,则a2+b2=c2
C.若a,b,c是Rt△ABC的三边,∠A=90°,则a2+b2=c2
D.若a,b,c是Rt△ABC的三边,∠C=90°,则a2+b2=c2
D
2.利用如图(1)或(2)所示的两个图形中的有关面积的等量关系
都能证明数学中一个十分著名的定理,这个定理称为___________,
该定理中结论的数学解析式是_____________.
勾股定理
a2+b2=c2
3.(练习1变式)求图中直角三角形中未知边的长度:c=___,b=___.
4.如图,正方形B的面积是_____.
15
12
144
8
B
B
8.(习题1变式)在△ABC中,∠C=90°,
∠A,∠B,∠C的对边分别是a,b,c.
(1)若b=2,c=3,求a的值;
(2)若a∶c=3∶5,b=28,求a,c的值.
9.(习题2变式)如图,一艘帆船由于风向的原因,先向正东方航行了
150千米,然后向正北方航行了80千米,这时它离出发点有多远?
解:由图知:AB=150,BC=80,△ABC构成直角三角形,
其中∠B=90°,根据勾股定理得AC2=AB2+BC2,
∴AC2=1502+802,∴AC=170,则这时它离出发点有170千米
10.如图,直线l同侧有三个正方形a,b,c,
若a,c的面积分别为5和11,则b的面积为(
)
A.4
B.6
C.16
D.55
C
A
12.(练习2变式)如图,图中所有的四边形都是正方形,
所有的三角形都是直角三角形,其中最大的正方形E的边长为7
cm,
则正方形A,B,C,D的面积之和是________.
49
cm2
13.(2019·通辽)腰长为5,高为4的等腰三角形的底边长为_____________.
14.(1)(原创题)如图,在四边形ABCD中,AB=3,BC=4,AD=13,
BC⊥AB,对角线AC⊥CD,求CD的长;
(2)如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,
求AB的长.
15.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,
其中的“面积法”给了小聪以灵感,他惊喜的发现,
当两个全等的直角三角形如图①或图②摆放时,
都可以用“面积法”来证明,下面是小聪利用图①证明勾股定理的过程:
将两个全等的直角三角形按图①所示摆放,
其中∠DAB=90°,求证:a2+b2=c2.
