第三章 图形的平移与旋转单元检测题1(含答案)
文档属性
| 名称 | 第三章 图形的平移与旋转单元检测题1(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 786.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 00:00:00 | ||
图片预览



文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版2020-2021学年度下学期八年级数学(下册)
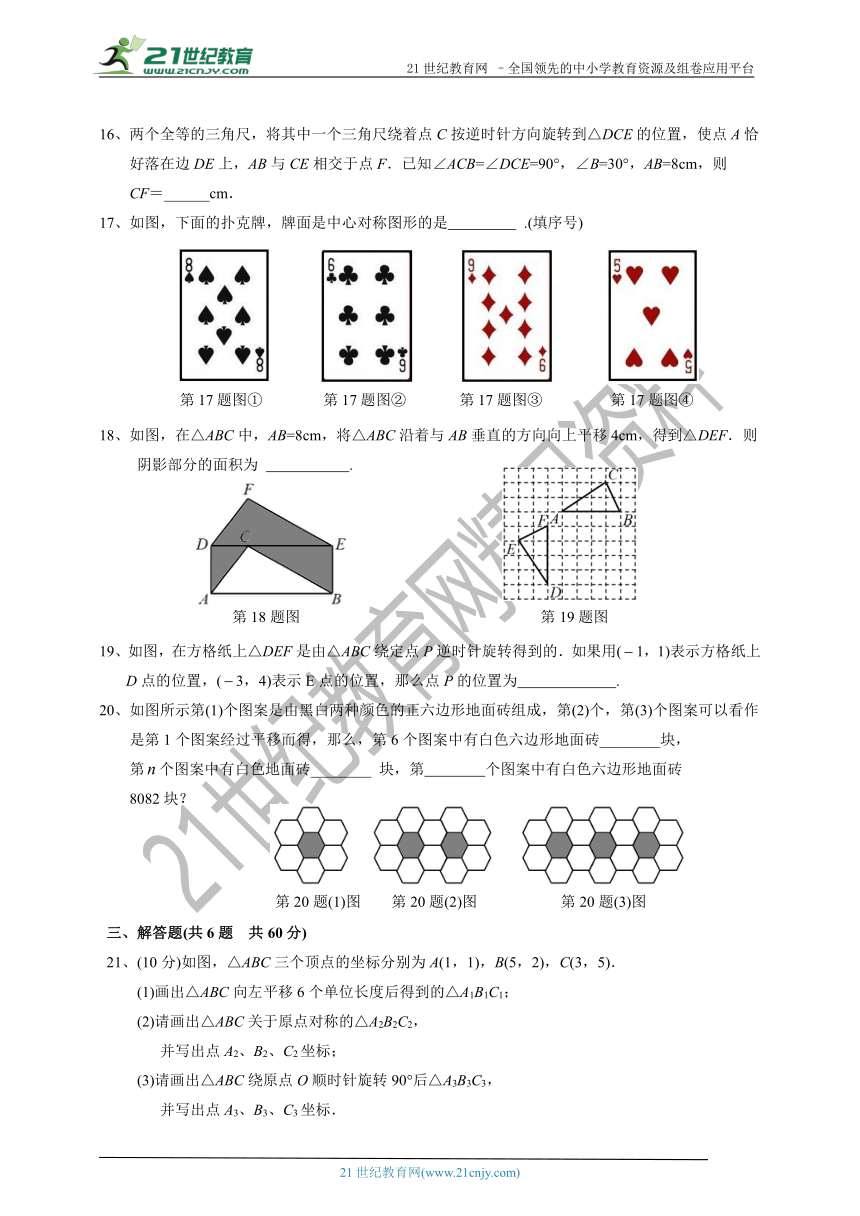
第三章图形的平移与旋转检测题1(有答案)
(时间:100分钟
满分:120分)
一、选择题
(每小题3分,共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
1、下列图形中,能由一个基本图案旋转得到的图形共有( )
A.1个
B.2个
C.3个
D.4个
2、在平面直角坐标系中,将△ABC绕着原点旋转180°后,得到△A1B1C1,则在这个过程可以看作( )
A.可以通过一次平移和一次对称得到
B.可以通过两次对称得到
C.可以通过两次平移得到
D.可以通过一次平移和一次旋转得到
3、如图,将周长为15cm的△ABC沿BC方向平移4cm得到△DEF,则下列命题中不正确的为(
)
A.AB∥DE,AB=DE
B.∠ACB=∠F
C.四边形ABFD周长为23cm
D.平移距离为线段EC的长度
4、如图,△ABC与△关于点O成中心对称,则下列结论不成立的是(
)
A.AO=
B.∠ACB=
∠
C.AB∥
D.BC=
5、在平面直角坐标系中,将△ABC向左平移5个单位后,再向下平移3个单位,
,P(a,b)是
△ABC边上的任意一点,则点P的对应点P1的坐标是(
)
A.(a+5,b+3)
B.(a5,b+3)
C.(a5,b3)
B.(5a,b3)
6、如图,在△OAB中,∠ABO=90°,将△OAB绕点O按顺时针方向旋转90°,得到△O,则点A的对应点的坐标为(
)
A.(4,
3)
B.(3,4)
C.(4,3)
D.(3,4)
7、如图,将网格中的三条线沿网格线的方向(水平或垂直)平移后组成一个首尾依次相接的三角
形,至少要移动( )
A.10格
B.13格
C.11格
D.14格
8、如图,图形旋转一定角度后能与自身重合,则旋转的角度可能是(
)
A.36°
B.90°
C.72°
D.108°
9、如图,Rt△ABC的直角边AB=10
cm,∠ABC=90°,∠C=30°,将绕点A逆时针旋转15°后得到△ABC,
则阴影部分的面积等于( )cm2
A.100
B.25
C.50
D.75
10、一个图形无论经过平移还是旋转,正确的说法有(
)
①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都没有发生变化.
A.②③④
B.①②④
C.①③④
D.①②③
二、填空题
(每题3分,共30分)
11、在平面直角坐标系中,点A(3a2b3,4)与(5,4a+7b5)关于原点成中心对称,则点
的坐标为
.
12、在平面直角坐标系中,△ABC的三个顶点是坐标分别是A
(2,3),B
(4,1),C
(2,0),
将△ABC一次平移至△A1B1C1的位置,点A、B、C的对应点分别是A1、B1、C1,若点A1的坐标为(3,0),则一次平移的方向
,距离是
.
13、观察如图,在平移、轴对称、旋转三种图形变换中,该图案不包含的变换
.
14、如图,点P是等边△ABC内一点,若PA=6,PB=8,PC=10,将△ABP绕点A旋转到△,则∠APB=
,=
.
15、如图,将△ABC沿着点C到A的方向平移到△DEF的位置,若则阴影部分面积为a,四边形BCFG的面积为
.
16、两个全等的三角尺,将其中一个三角尺绕着点C按逆时针方向旋转到△DCE的位置,使点A恰
好落在边DE上,AB与CE相交于点F.已知∠ACB=∠DCE=90°,∠B=30°,AB=8cm,则
CF=______cm.
17、如图,下面的扑克牌,牌面是中心对称图形的是
.(填序号)
18、如图,在△ABC中,AB=8cm,将△ABC沿着与AB垂直的方向向上平移4cm,得到△DEF.则
阴影部分的面积为
.
19、如图,在方格纸上△DEF是由△ABC绕定点P逆时针旋转得到的.如果用(1,1)表示方格纸上D点的位置,(3,4)表示E点的位置,那么点P的位置为
.
20、如图所示第(1)个图案是由黑白两种颜色的正六边形地面砖组成,第(2)个,第(3)个图案可以看作
是第1个图案经过平移而得,那么,第6个图案中有白色六边形地面砖________块,
第个图案中有白色地面砖________
块,第
个图案中有白色六边形地面砖
8082块?
三、解答题(共6题
共60分)
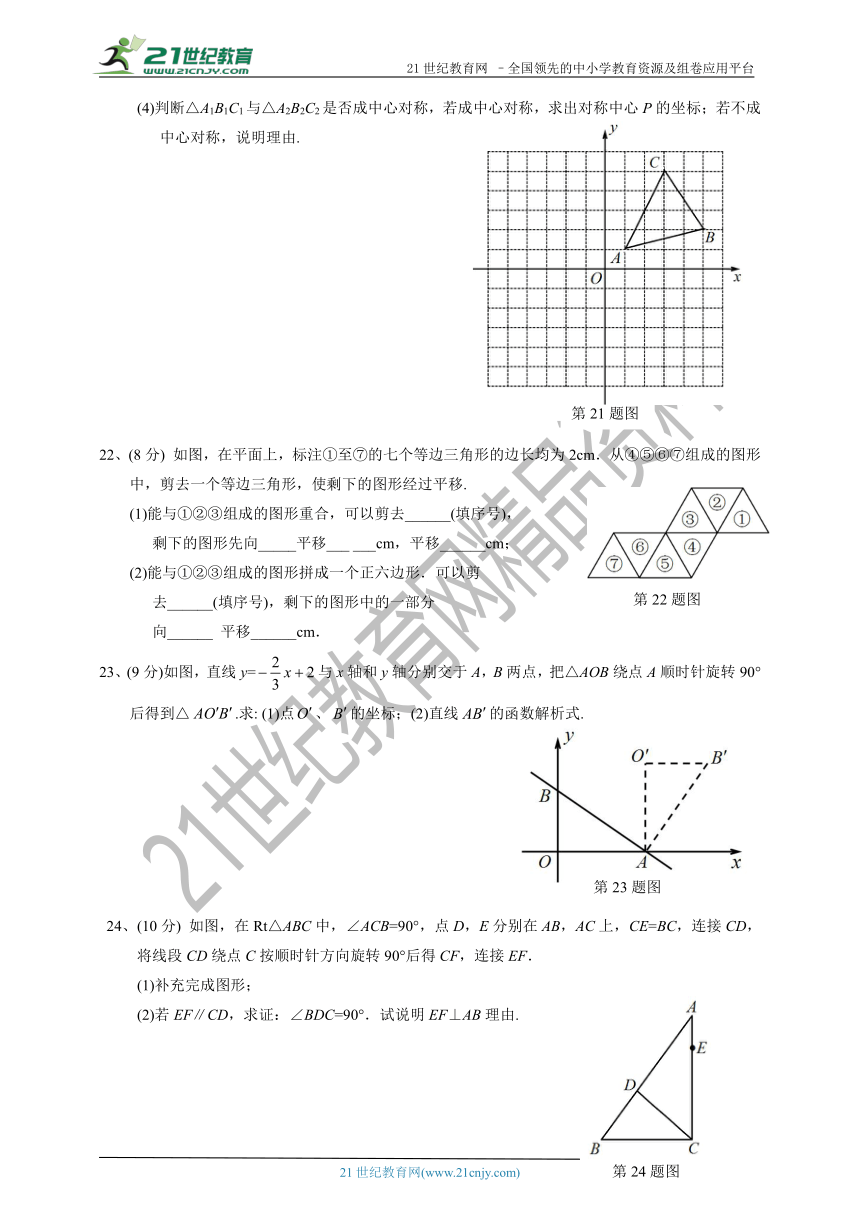
21、(10分)如图,△ABC三个顶点的坐标分别为A(1,1),B(5,2),C(3,5).
(1)画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2,
并写出点A2、B2、C2坐标;
(3)请画出△ABC绕原点O顺时针旋转90°后△A3B3C3,
并写出点A3、B3、C3坐标.
(4)判断△A1B1C1与△A2B2C2是否成中心对称,若成中心对称,求出对称中心P的坐标;若不成中心对称,说明理由.
22、(8分)
如图,在平面上,标注①至⑦的七个等边三角形的边长均为2cm.从④⑤⑥⑦组成的图形
中,剪去一个等边三角形,使剩下的图形经过平移.
(1)能与①②③组成的图形重合,可以剪去______(填序号),
剩下的图形先向_____平移___
___cm,平移______cm;
(2)能与①②③组成的图形拼成一个正六边形.可以剪
去______(填序号),剩下的图形中的一部分
向______
平移______cm.
23、(9分)如图,直线y=与x轴和y轴分别交于A,B两点,把△AOB绕点A顺时针旋转90°后得到△.求:
(1)点、的坐标;(2)直线的函数解析式.
24、(10分)
如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.试说明EF⊥AB理由.
25、(11分)
如图,在△ABC中,AB=AC,
∠BAC=120°,点D,E为BC边上的动点,满足∠DAE=60°,
若BD=3cm,EC=4cm,
求DE的长.
26、(12分)
如图,△ABC中,∠ACB=90?,AC=BC=1,将△ABC绕点C逆时针旋转角α
(0?<α<90?)得到△A1B1C1,连结BB1.若CB1交AB于D,A1B1分别交AB、AC于E、F.
(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以证明(△ABC
与△A1B1C1全等除外);
(2)当△BB1D是等腰三角形时,求α;
(3)根据(2)的结果,求BD的长.
???????
??????
参考答案
一、选择题(共10小题
每3分
共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
B
D
B
C
D
A
C
C
A
二、填空题(共10小题
每题3分
共30分)
11、(2,4)
12、BB1,5
13、平移
14、150°,6
15、a
16、
17、①③
18、32cm2
19、(2,3)
20、26,2+4n,2020
三、解答题(共6题
共60分)
21、(10分)如图,△ABC三个顶点的坐标分别为A(1,1),B(5,2),C(3,5).
(1)画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2,
并写出点A2、B2、C2坐标;
(3)请画出△ABC绕原点O顺时针旋转90°后△A3B3C3,
并写出点A3、B3、C3坐标.
(4)判断△A1B1C1与△A2B2C2是否成中心对称,若成中心对称,求出对称中心P的坐标;若不成中心对称,说明理由.
解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,
点A2、B2、C2坐标分别
为(1,1),(5,2),(3,5);
(3)如图,△A3B3C3为所作,
点A3、B3、C3坐标分别
为(1,1),(2,5),(5,3).
(4)△A1B1C1与△A2B2C2是中心对称图形,
对称中心P坐标为
(3,0).
22、(8分)
如图,在平面上,标注①至⑦的七个等边三角形的边长均为2cm.从④⑤⑥⑦组成的图形
中,剪去一个等边三角形,使剩下的图形经过平移.
(1)能与①②③组成的图形重合,可以剪去___④___(填序号),
剩下的图形先向__左___平移______cm,平移___2___cm;
(2)能与①②③组成的图形拼成一个正六边形.可以剪
去___⑤___(填序号),剩下的图形中的一部分
向___上___平移___2___cm.
23、(9分)如图,直线y=与x轴和y轴分别交于A,B两点,把△AOB绕点A顺时针旋转90°后得到△.求:
(1)点、的坐标;(2)直线的函数解析式.
解:(1)令x=0,则y=2,∴点B的坐标(0,2),
∴OB==2;
令y=0,则,
解得,x=3,
∴点A的坐标为(3,0),
∴OA==3;
当把△AOB绕点A顺时针旋转90°后,
∴⊥x轴,=90°,
∴∥x轴,OA+=3+2=5,
∴点的坐标为(3,3),点的坐标为(5,3);
(2)设直线的函数解析式为y=kx+b,
把A(3,0),(5,3)代入得,
,解得,
∴直线的函数解析式为.
24、(10分)
如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.试说明EF⊥AB理由.
解:(1)补充完成图形如图第24题图(1)
由旋转的性质得:∠DCF=90°,
∴∠DCE+∠ECF=90°,
∵∠ACB=90°,
∴∠DCE+∠BCD=90°,
∴∠BCD
=∠ECF,
∵EF∥DC,
∴∠EFC+∠DCF=180°,
∴∠EFC=90°,
在△BDC和△EFC中,
∵,
∴△BDC≌△EFC(SAS),
∴∠BDC=∠EFC=90°
∴CD⊥AB,
∴EF⊥AB.
25、(11分)
如图,在△ABC中,AB=AC,
∠BAC=120°,点D,E为BC边上的动点,满足∠DAE=60°,
若BD=3cm,EC=4cm,
求DE的长.
解:(1)∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
将△AEC绕着点A顺时针到△的位置,
连接,过点作垂直CB的延长线于点M,
∴=AE,∠=∠C=30°,∠=∠+∠ABC=30°+30°=60°,∠AB=∠EAC,
=EC=4cm,
∵∠BAC
=120°,∠DAE=60°,
∴∠BAD+∠EAC=∠BAC∠DAE=120°60°=60°,
∴∠AD=
∠BAD
+∠AB
=∠BAD+∠EAC=60°,
∴∠AD=
∠EAD;
在△AD和△EAD中,
∵,
∴△AD≌△EAD(SAS),
∴D=ED.
在Rt△中,∠=60°,则,
∴MB=
cm,
∴cm,
∵BD=3cm,
∴MD=
BDBM
=32=1
cm,
在Rt△中,
cm,
DE=cm.
26、(12分)
如图,△ABC中,∠ACB=90?,AC=BC=1,将△ABC绕点C逆时针旋转角α
(0?<α<90?)得到△A1B1C1,连结BB1.若CB1交AB于D,A1B1分别交AB、AC于E、F.
(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以证明(△ABC与△A1B1C1全等除外);
(2)当△BB1D是等腰三角形时,求α;
(3)根据(2)的结果,求BD的长.
解:(1)全等的三角形有:
△CBD≌△CA1F或△AEF≌△B1ED或△ACD≌△B1CF等.(只需写一个即可)
以证△CBD≌△CA1F为例:
证明:∵∠ACB1+∠A1CF=∠ACB1+∠BCD=90?
∴∠A1CF=∠BCD,
∵∠ACB=90?,AC=BC=1,
∴∠A=∠B=45
?,
∵△A1B1C1是△ABC绕点C逆时针旋转角α得到的,
∴A1C=B1C=1,∠A1=∠B1=45
?,
在△A1CF和△BCD中,
∵,
∴△A1CF≌△BCD(AAS),
(2)在△CBB1中,∵CB=CB1,
∴∠CBB1=∠CB1B==,
又△ABC是等腰直角三角形,∴∠ABC=45°?,?????
①若B1B=B1D,则∠B1DB=∠B1BD,
∵∠B1DB=45°+α,
∠B1BD=∠CBB1-45°=45°=45°,
∴45°+α=45°,解得=0°(舍去);
②∵∠CBB1=∠CB1B
>∠B1BD
∴BD>B1D,即BD≠B1D;
③若BB1=BD,则∠BDB1=∠BB1D,即45°+α=90°,
解得=30°;
由①②③可知,当△BB1D为等腰三角形时,α=30°?;?????
(3)作DG⊥BC于G,设DB=x
在Rt△DBG中,∠B=45°,∴∠BDG=45°
,
∴DG=BG=,
在Rt△DCG中,∠C=∠α=30°,
∴DC=2DG=,
∴CG=,
∵CB=CG+GB=+=1,
∴x=,
∴BD=.
第25题图
第23题图
第3题图
第14题图
第7题图
第24题图
第23题图
第22题图
第26题图
第15题图
第25题图
第20题(1)图
第20题(2)图
第20题(3)图
第21题图
第22题图
第26题图
第25题图
第21题图
第24题图(1)
第21题图
第17题图①
第17题图②
第17题图③
第17题图④
第18题图
第13题图
第19题图
第16题图
第9题图
第26题图
第24题图
第8题图
第6题图
第4题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版2020-2021学年度下学期八年级数学(下册)
第三章图形的平移与旋转检测题1(有答案)
(时间:100分钟
满分:120分)
一、选择题
(每小题3分,共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
1、下列图形中,能由一个基本图案旋转得到的图形共有( )
A.1个
B.2个
C.3个
D.4个
2、在平面直角坐标系中,将△ABC绕着原点旋转180°后,得到△A1B1C1,则在这个过程可以看作( )
A.可以通过一次平移和一次对称得到
B.可以通过两次对称得到
C.可以通过两次平移得到
D.可以通过一次平移和一次旋转得到
3、如图,将周长为15cm的△ABC沿BC方向平移4cm得到△DEF,则下列命题中不正确的为(
)
A.AB∥DE,AB=DE
B.∠ACB=∠F
C.四边形ABFD周长为23cm
D.平移距离为线段EC的长度
4、如图,△ABC与△关于点O成中心对称,则下列结论不成立的是(
)
A.AO=
B.∠ACB=
∠
C.AB∥
D.BC=
5、在平面直角坐标系中,将△ABC向左平移5个单位后,再向下平移3个单位,
,P(a,b)是
△ABC边上的任意一点,则点P的对应点P1的坐标是(
)
A.(a+5,b+3)
B.(a5,b+3)
C.(a5,b3)
B.(5a,b3)
6、如图,在△OAB中,∠ABO=90°,将△OAB绕点O按顺时针方向旋转90°,得到△O,则点A的对应点的坐标为(
)
A.(4,
3)
B.(3,4)
C.(4,3)
D.(3,4)
7、如图,将网格中的三条线沿网格线的方向(水平或垂直)平移后组成一个首尾依次相接的三角
形,至少要移动( )
A.10格
B.13格
C.11格
D.14格
8、如图,图形旋转一定角度后能与自身重合,则旋转的角度可能是(
)
A.36°
B.90°
C.72°
D.108°
9、如图,Rt△ABC的直角边AB=10
cm,∠ABC=90°,∠C=30°,将绕点A逆时针旋转15°后得到△ABC,
则阴影部分的面积等于( )cm2
A.100
B.25
C.50
D.75
10、一个图形无论经过平移还是旋转,正确的说法有(
)
①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都没有发生变化.
A.②③④
B.①②④
C.①③④
D.①②③
二、填空题
(每题3分,共30分)
11、在平面直角坐标系中,点A(3a2b3,4)与(5,4a+7b5)关于原点成中心对称,则点
的坐标为
.
12、在平面直角坐标系中,△ABC的三个顶点是坐标分别是A
(2,3),B
(4,1),C
(2,0),
将△ABC一次平移至△A1B1C1的位置,点A、B、C的对应点分别是A1、B1、C1,若点A1的坐标为(3,0),则一次平移的方向
,距离是
.
13、观察如图,在平移、轴对称、旋转三种图形变换中,该图案不包含的变换
.
14、如图,点P是等边△ABC内一点,若PA=6,PB=8,PC=10,将△ABP绕点A旋转到△,则∠APB=
,=
.
15、如图,将△ABC沿着点C到A的方向平移到△DEF的位置,若则阴影部分面积为a,四边形BCFG的面积为
.
16、两个全等的三角尺,将其中一个三角尺绕着点C按逆时针方向旋转到△DCE的位置,使点A恰
好落在边DE上,AB与CE相交于点F.已知∠ACB=∠DCE=90°,∠B=30°,AB=8cm,则
CF=______cm.
17、如图,下面的扑克牌,牌面是中心对称图形的是
.(填序号)
18、如图,在△ABC中,AB=8cm,将△ABC沿着与AB垂直的方向向上平移4cm,得到△DEF.则
阴影部分的面积为
.
19、如图,在方格纸上△DEF是由△ABC绕定点P逆时针旋转得到的.如果用(1,1)表示方格纸上D点的位置,(3,4)表示E点的位置,那么点P的位置为
.
20、如图所示第(1)个图案是由黑白两种颜色的正六边形地面砖组成,第(2)个,第(3)个图案可以看作
是第1个图案经过平移而得,那么,第6个图案中有白色六边形地面砖________块,
第个图案中有白色地面砖________
块,第
个图案中有白色六边形地面砖
8082块?
三、解答题(共6题
共60分)
21、(10分)如图,△ABC三个顶点的坐标分别为A(1,1),B(5,2),C(3,5).
(1)画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2,
并写出点A2、B2、C2坐标;
(3)请画出△ABC绕原点O顺时针旋转90°后△A3B3C3,
并写出点A3、B3、C3坐标.
(4)判断△A1B1C1与△A2B2C2是否成中心对称,若成中心对称,求出对称中心P的坐标;若不成中心对称,说明理由.
22、(8分)
如图,在平面上,标注①至⑦的七个等边三角形的边长均为2cm.从④⑤⑥⑦组成的图形
中,剪去一个等边三角形,使剩下的图形经过平移.
(1)能与①②③组成的图形重合,可以剪去______(填序号),
剩下的图形先向_____平移___
___cm,平移______cm;
(2)能与①②③组成的图形拼成一个正六边形.可以剪
去______(填序号),剩下的图形中的一部分
向______
平移______cm.
23、(9分)如图,直线y=与x轴和y轴分别交于A,B两点,把△AOB绕点A顺时针旋转90°后得到△.求:
(1)点、的坐标;(2)直线的函数解析式.
24、(10分)
如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.试说明EF⊥AB理由.
25、(11分)
如图,在△ABC中,AB=AC,
∠BAC=120°,点D,E为BC边上的动点,满足∠DAE=60°,
若BD=3cm,EC=4cm,
求DE的长.
26、(12分)
如图,△ABC中,∠ACB=90?,AC=BC=1,将△ABC绕点C逆时针旋转角α
(0?<α<90?)得到△A1B1C1,连结BB1.若CB1交AB于D,A1B1分别交AB、AC于E、F.
(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以证明(△ABC
与△A1B1C1全等除外);
(2)当△BB1D是等腰三角形时,求α;
(3)根据(2)的结果,求BD的长.
???????
??????
参考答案
一、选择题(共10小题
每3分
共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
B
D
B
C
D
A
C
C
A
二、填空题(共10小题
每题3分
共30分)
11、(2,4)
12、BB1,5
13、平移
14、150°,6
15、a
16、
17、①③
18、32cm2
19、(2,3)
20、26,2+4n,2020
三、解答题(共6题
共60分)
21、(10分)如图,△ABC三个顶点的坐标分别为A(1,1),B(5,2),C(3,5).
(1)画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2,
并写出点A2、B2、C2坐标;
(3)请画出△ABC绕原点O顺时针旋转90°后△A3B3C3,
并写出点A3、B3、C3坐标.
(4)判断△A1B1C1与△A2B2C2是否成中心对称,若成中心对称,求出对称中心P的坐标;若不成中心对称,说明理由.
解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作,
点A2、B2、C2坐标分别
为(1,1),(5,2),(3,5);
(3)如图,△A3B3C3为所作,
点A3、B3、C3坐标分别
为(1,1),(2,5),(5,3).
(4)△A1B1C1与△A2B2C2是中心对称图形,
对称中心P坐标为
(3,0).
22、(8分)
如图,在平面上,标注①至⑦的七个等边三角形的边长均为2cm.从④⑤⑥⑦组成的图形
中,剪去一个等边三角形,使剩下的图形经过平移.
(1)能与①②③组成的图形重合,可以剪去___④___(填序号),
剩下的图形先向__左___平移______cm,平移___2___cm;
(2)能与①②③组成的图形拼成一个正六边形.可以剪
去___⑤___(填序号),剩下的图形中的一部分
向___上___平移___2___cm.
23、(9分)如图,直线y=与x轴和y轴分别交于A,B两点,把△AOB绕点A顺时针旋转90°后得到△.求:
(1)点、的坐标;(2)直线的函数解析式.
解:(1)令x=0,则y=2,∴点B的坐标(0,2),
∴OB==2;
令y=0,则,
解得,x=3,
∴点A的坐标为(3,0),
∴OA==3;
当把△AOB绕点A顺时针旋转90°后,
∴⊥x轴,=90°,
∴∥x轴,OA+=3+2=5,
∴点的坐标为(3,3),点的坐标为(5,3);
(2)设直线的函数解析式为y=kx+b,
把A(3,0),(5,3)代入得,
,解得,
∴直线的函数解析式为.
24、(10分)
如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.试说明EF⊥AB理由.
解:(1)补充完成图形如图第24题图(1)
由旋转的性质得:∠DCF=90°,
∴∠DCE+∠ECF=90°,
∵∠ACB=90°,
∴∠DCE+∠BCD=90°,
∴∠BCD
=∠ECF,
∵EF∥DC,
∴∠EFC+∠DCF=180°,
∴∠EFC=90°,
在△BDC和△EFC中,
∵,
∴△BDC≌△EFC(SAS),
∴∠BDC=∠EFC=90°
∴CD⊥AB,
∴EF⊥AB.
25、(11分)
如图,在△ABC中,AB=AC,
∠BAC=120°,点D,E为BC边上的动点,满足∠DAE=60°,
若BD=3cm,EC=4cm,
求DE的长.
解:(1)∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
将△AEC绕着点A顺时针到△的位置,
连接,过点作垂直CB的延长线于点M,
∴=AE,∠=∠C=30°,∠=∠+∠ABC=30°+30°=60°,∠AB=∠EAC,
=EC=4cm,
∵∠BAC
=120°,∠DAE=60°,
∴∠BAD+∠EAC=∠BAC∠DAE=120°60°=60°,
∴∠AD=
∠BAD
+∠AB
=∠BAD+∠EAC=60°,
∴∠AD=
∠EAD;
在△AD和△EAD中,
∵,
∴△AD≌△EAD(SAS),
∴D=ED.
在Rt△中,∠=60°,则,
∴MB=
cm,
∴cm,
∵BD=3cm,
∴MD=
BDBM
=32=1
cm,
在Rt△中,
cm,
DE=cm.
26、(12分)
如图,△ABC中,∠ACB=90?,AC=BC=1,将△ABC绕点C逆时针旋转角α
(0?<α<90?)得到△A1B1C1,连结BB1.若CB1交AB于D,A1B1分别交AB、AC于E、F.
(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以证明(△ABC与△A1B1C1全等除外);
(2)当△BB1D是等腰三角形时,求α;
(3)根据(2)的结果,求BD的长.
解:(1)全等的三角形有:
△CBD≌△CA1F或△AEF≌△B1ED或△ACD≌△B1CF等.(只需写一个即可)
以证△CBD≌△CA1F为例:
证明:∵∠ACB1+∠A1CF=∠ACB1+∠BCD=90?
∴∠A1CF=∠BCD,
∵∠ACB=90?,AC=BC=1,
∴∠A=∠B=45
?,
∵△A1B1C1是△ABC绕点C逆时针旋转角α得到的,
∴A1C=B1C=1,∠A1=∠B1=45
?,
在△A1CF和△BCD中,
∵,
∴△A1CF≌△BCD(AAS),
(2)在△CBB1中,∵CB=CB1,
∴∠CBB1=∠CB1B==,
又△ABC是等腰直角三角形,∴∠ABC=45°?,?????
①若B1B=B1D,则∠B1DB=∠B1BD,
∵∠B1DB=45°+α,
∠B1BD=∠CBB1-45°=45°=45°,
∴45°+α=45°,解得=0°(舍去);
②∵∠CBB1=∠CB1B
>∠B1BD
∴BD>B1D,即BD≠B1D;
③若BB1=BD,则∠BDB1=∠BB1D,即45°+α=90°,
解得=30°;
由①②③可知,当△BB1D为等腰三角形时,α=30°?;?????
(3)作DG⊥BC于G,设DB=x
在Rt△DBG中,∠B=45°,∴∠BDG=45°
,
∴DG=BG=,
在Rt△DCG中,∠C=∠α=30°,
∴DC=2DG=,
∴CG=,
∵CB=CG+GB=+=1,
∴x=,
∴BD=.
第25题图
第23题图
第3题图
第14题图
第7题图
第24题图
第23题图
第22题图
第26题图
第15题图
第25题图
第20题(1)图
第20题(2)图
第20题(3)图
第21题图
第22题图
第26题图
第25题图
第21题图
第24题图(1)
第21题图
第17题图①
第17题图②
第17题图③
第17题图④
第18题图
第13题图
第19题图
第16题图
第9题图
第26题图
第24题图
第8题图
第6题图
第4题图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
