2020-2021学年人教版数学七年级下册5.2.2平行线的判定-课件(共14张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学七年级下册5.2.2平行线的判定-课件(共14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
1
七年级-下册-5.2.2
难点名称:平行线的判定方法1的应用,用符号语言进行简单的推理
同位角相等,两直线平行
目录
CONTENTS
2
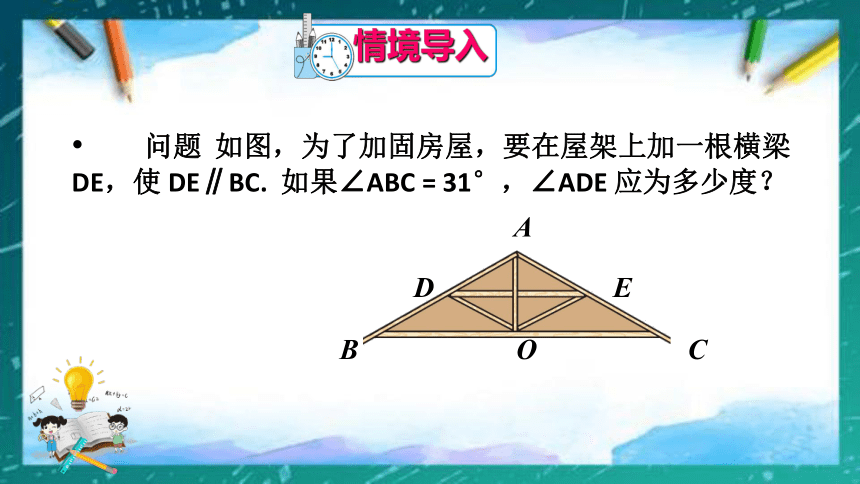
问题
如图,为了加固房屋,要在屋架上加一根横梁
DE,使
DE∥BC.
如果∠ABC
=
31°,∠ADE
应为多少度?
情境导入
A
D
E
B
O
C
(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
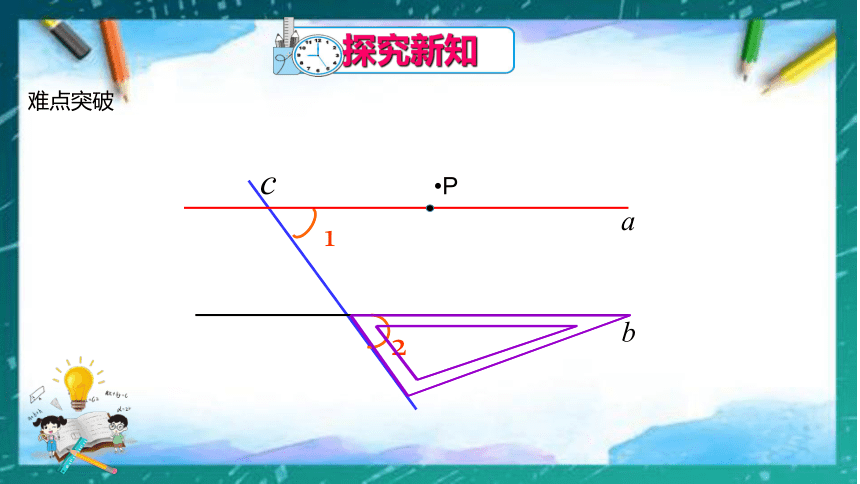
探究新知
你还记得如何用直尺和三角尺画平行线吗?
(3)你能得出一个判定两直线平行的方法吗?
难点突破
b
c
2
1
a
P
探究新知
难点突破
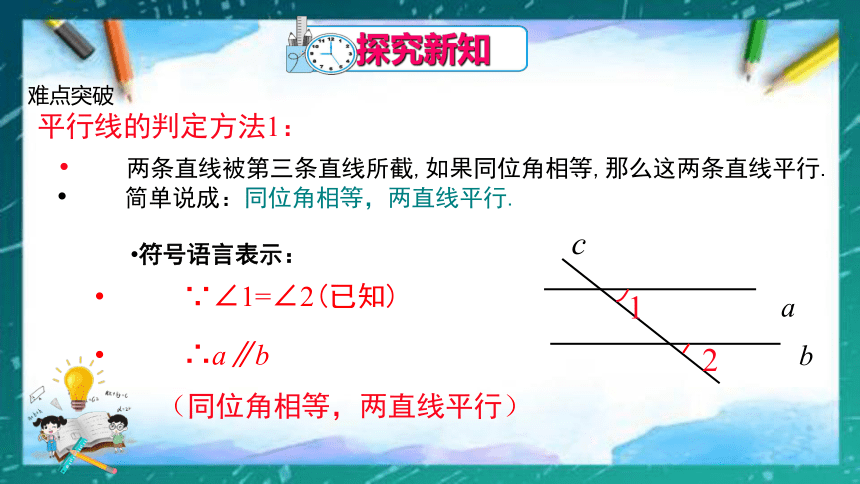
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
符号语言表示:
∵∠1=∠2(已知)
∴a∥b
(同位角相等,两直线平行)
1
2
a
b
c
平行线的判定方法1:
探究新知
难点突破
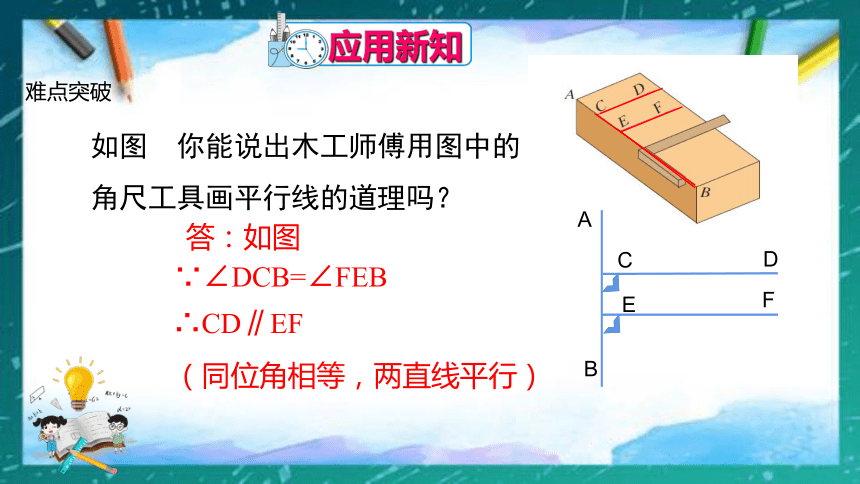
如图
你能说出木工师傅用图中的角尺工具画平行线的道理吗?
∵∠DCB=∠FEB
C
E
D
F
A
B
∴CD∥EF
(同位角相等,两直线平行)
答:如图
应用新知
难点突破
问题
如图,为了加固房屋,
要在屋架上加一根横梁
DE,使
DE∥BC.
如果∠ABC
=
31°,∠ADE
应为多少度?
因为∠ADE
和∠ABC是直线DE、BC被直线AB截得的同位角,所以当∠ADE=∠ABC
=
31°时,DE∥BC
,依据“同位角相等,两直线平行”。
A
D
E
B
O
C
应用新知
答:
难点突破
1.
如图,
BE
是
AB
的延长线.
由∠CBE
=∠A
可以判定哪两条直线平行?根据是什么?
答:
AD∥BC
.
根据
∵∠CBE=∠A(已知)
∴AD∥BC
(同位角相等,两直线平行)
课堂练习
难点巩固
2.
如图,当∠1=∠3
时,直线
a,b
平行吗?当∠2
+
∠3
=
180°时,直线
a,b
平行吗?为什么?
解:如图所示:
当∠1
=∠3
时,a∥b
.
理由:∵∠1
=∠3(已知),
又∵
∠1
=∠4(对顶角相等),
∴
∠3
=∠4(等量代换),
∴a∥b(同位
角相等,两
直
线
平
行).
4
课堂练习
难点巩固
当∠2+∠3
=
180°时,a∥b
.
理由:∵∠2+∠3
=
180°(已知),
又∵∠2+∠4
=
180°(邻补角定义),
∴∠3
=∠4(同角的补角相等),
∴a∥b(同位角相等,两直线平行).
4
当∠2
+
∠3
=
180°时,直线
a,b
平行吗?为什么?
课堂练习
难点巩固
当∠2+∠3
=
180°时,a∥b
.
理由:∵∠2+∠3
=
180°(已知),
又∵∠2+∠4
=
180°
(邻补角定义),
∴∠3
=∠4
(同角的补角相等),
∴a∥b
(同位角相等,两直线平行).
4
解:如图所示:
当∠1
=∠3
时,a∥b
.
理由:∵∠1
=∠3(已知),
又∵
∠1
=∠4
(对顶角相等),
∴
∠3
=∠4
(等量代换),
∴a∥b
(同位
角相等,两
直
线
平
行).
课堂练习
难点巩固
解题时要注意:
用判定方法1来判定两直线平行,主要是通过找同位角来实现.
正确区分截线和被截线是判定两直线平行的关键.
课堂小结
分析问题时要把题目中给出的条件转化到图形当中。
推理过程中要结合图形用规范的符号语言表达,推理步骤应条理清晰。
这节课我们学行线的判定方法1:同位角相等,两直线平行。
1
七年级-下册-5.2.2
难点名称:平行线的判定方法1的应用,用符号语言进行简单的推理
同位角相等,两直线平行
目录
CONTENTS
2
问题
如图,为了加固房屋,要在屋架上加一根横梁
DE,使
DE∥BC.
如果∠ABC
=
31°,∠ADE
应为多少度?
情境导入
A
D
E
B
O
C
(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
探究新知
你还记得如何用直尺和三角尺画平行线吗?
(3)你能得出一个判定两直线平行的方法吗?
难点突破
b
c
2
1
a
P
探究新知
难点突破
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
符号语言表示:
∵∠1=∠2(已知)
∴a∥b
(同位角相等,两直线平行)
1
2
a
b
c
平行线的判定方法1:
探究新知
难点突破
如图
你能说出木工师傅用图中的角尺工具画平行线的道理吗?
∵∠DCB=∠FEB
C
E
D
F
A
B
∴CD∥EF
(同位角相等,两直线平行)
答:如图
应用新知
难点突破
问题
如图,为了加固房屋,
要在屋架上加一根横梁
DE,使
DE∥BC.
如果∠ABC
=
31°,∠ADE
应为多少度?
因为∠ADE
和∠ABC是直线DE、BC被直线AB截得的同位角,所以当∠ADE=∠ABC
=
31°时,DE∥BC
,依据“同位角相等,两直线平行”。
A
D
E
B
O
C
应用新知
答:
难点突破
1.
如图,
BE
是
AB
的延长线.
由∠CBE
=∠A
可以判定哪两条直线平行?根据是什么?
答:
AD∥BC
.
根据
∵∠CBE=∠A(已知)
∴AD∥BC
(同位角相等,两直线平行)
课堂练习
难点巩固
2.
如图,当∠1=∠3
时,直线
a,b
平行吗?当∠2
+
∠3
=
180°时,直线
a,b
平行吗?为什么?
解:如图所示:
当∠1
=∠3
时,a∥b
.
理由:∵∠1
=∠3(已知),
又∵
∠1
=∠4(对顶角相等),
∴
∠3
=∠4(等量代换),
∴a∥b(同位
角相等,两
直
线
平
行).
4
课堂练习
难点巩固
当∠2+∠3
=
180°时,a∥b
.
理由:∵∠2+∠3
=
180°(已知),
又∵∠2+∠4
=
180°(邻补角定义),
∴∠3
=∠4(同角的补角相等),
∴a∥b(同位角相等,两直线平行).
4
当∠2
+
∠3
=
180°时,直线
a,b
平行吗?为什么?
课堂练习
难点巩固
当∠2+∠3
=
180°时,a∥b
.
理由:∵∠2+∠3
=
180°(已知),
又∵∠2+∠4
=
180°
(邻补角定义),
∴∠3
=∠4
(同角的补角相等),
∴a∥b
(同位角相等,两直线平行).
4
解:如图所示:
当∠1
=∠3
时,a∥b
.
理由:∵∠1
=∠3(已知),
又∵
∠1
=∠4
(对顶角相等),
∴
∠3
=∠4
(等量代换),
∴a∥b
(同位
角相等,两
直
线
平
行).
课堂练习
难点巩固
解题时要注意:
用判定方法1来判定两直线平行,主要是通过找同位角来实现.
正确区分截线和被截线是判定两直线平行的关键.
课堂小结
分析问题时要把题目中给出的条件转化到图形当中。
推理过程中要结合图形用规范的符号语言表达,推理步骤应条理清晰。
这节课我们学行线的判定方法1:同位角相等,两直线平行。
