2020-2021学年人教版 九年级数学下册 第二十七章 相似 综合训练(word解析版)
文档属性
| 名称 | 2020-2021学年人教版 九年级数学下册 第二十七章 相似 综合训练(word解析版) | 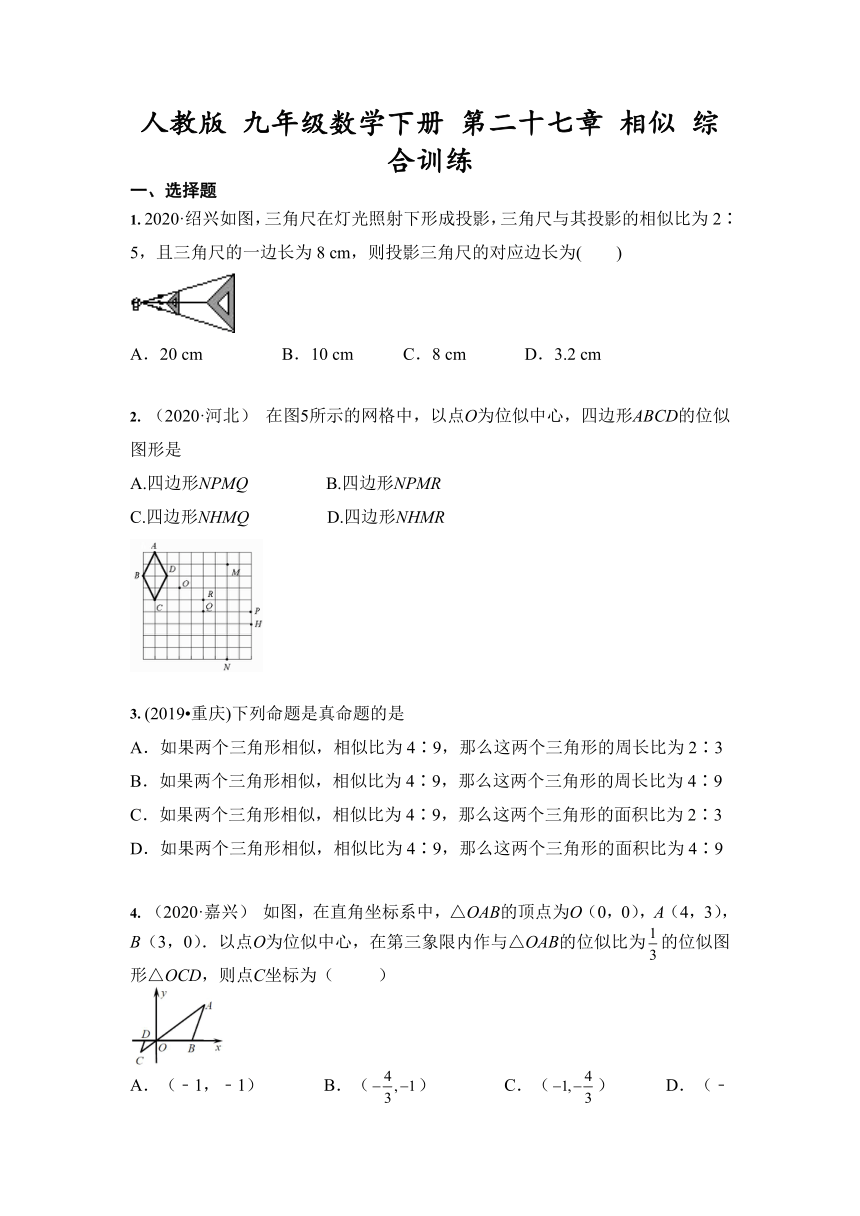 | |
| 格式 | doc | ||
| 文件大小 | 786.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-21 18:38:09 | ||
图片预览


文档简介
人教版 九年级数学下册 第二十七章 相似 综合训练
一、选择题
1. 2020·绍兴如图,三角尺在灯光照射下形成投影,三角尺与其投影的相似比为2∶5,且三角尺的一边长为8 cm,则投影三角尺的对应边长为( )
A.20 cm B.10 cm C.8 cm D.3.2 cm
2. (2020·河北) 在图5所示的网格中,以点O为位似中心,四边形ABCD的位似图形是
A.四边形NPMQ B.四边形NPMR
C.四边形NHMQ D.四边形NHMR
3. (2019?重庆)下列命题是真命题的是
A.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为2∶3
B.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9
C.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为2∶3
D.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为4∶9
4. (2020·嘉兴) 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点C坐标为( )
A.(﹣1,﹣1) B.() C.() D.(﹣2,﹣1)
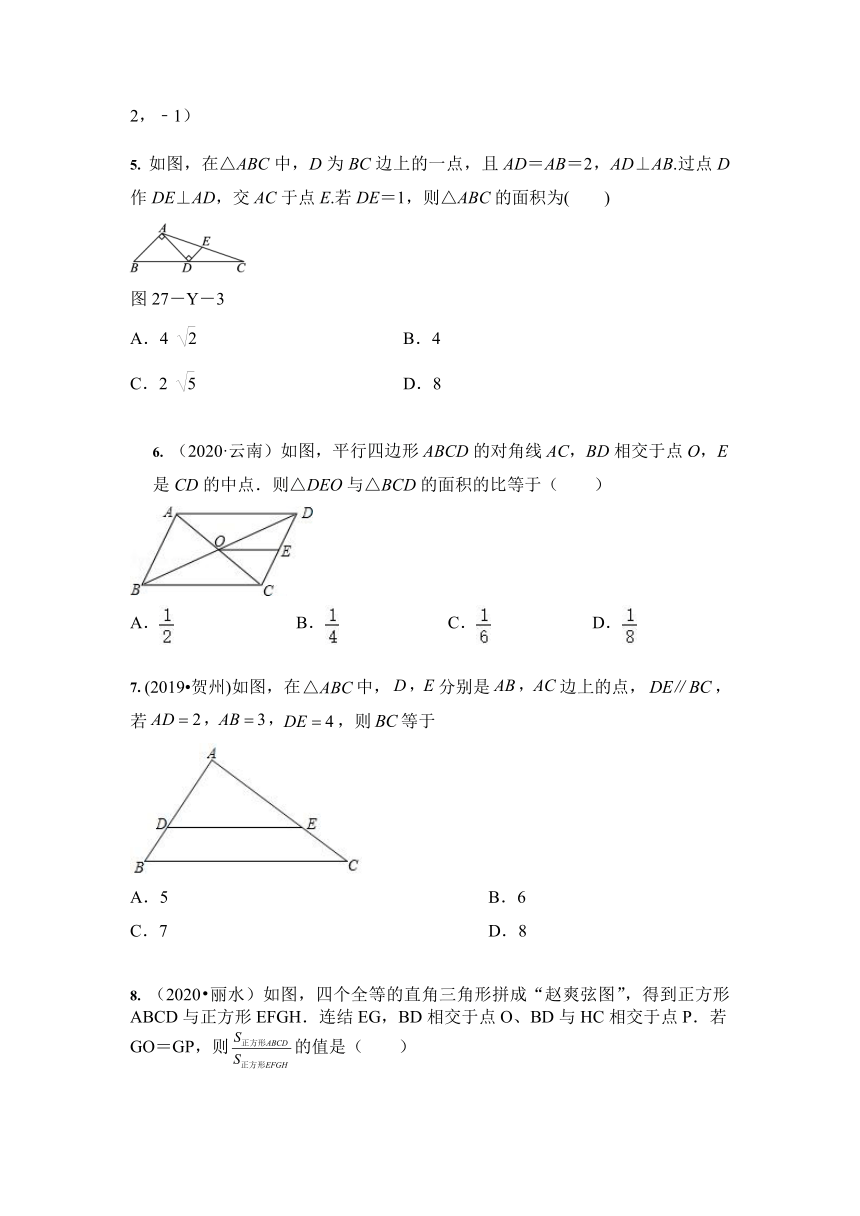
5. 如图,在△ABC中,D为BC边上的一点,且AD=AB=2,AD⊥AB.过点D作DE⊥AD,交AC于点E.若DE=1,则△ABC的面积为( )
图27-Y-3
A.4 B.4
C.2 D.8
6. (2020·云南)如图,平行四边形ABCD的对角线AC,BD相交于点O,E是CD的中点.则△DEO与△BCD的面积的比等于( )
A. B. C. D.
7. (2019?贺州)如图,在中,分别是边上的点,,若,则等于
A.5 B.6
C.7 D.8
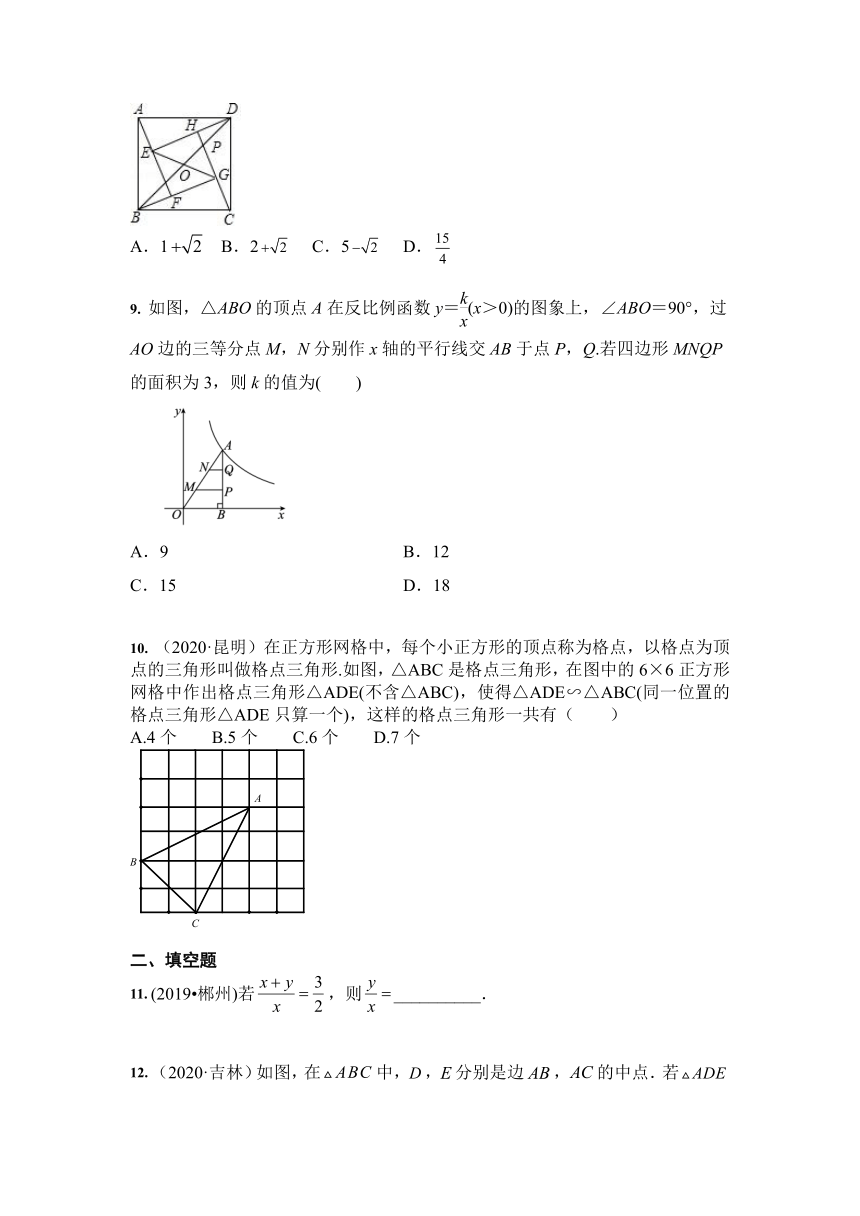
8. (2020?丽水)如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH.连结EG,BD相交于点O、BD与HC相交于点P.若GO=GP,则的值是( )
A.1 B.2 C.5 D.
9. 如图,△ABO的顶点A在反比例函数y=(x>0)的图象上,∠ABO=90°,过AO边的三等分点M,N分别作x轴的平行线交AB于点P,Q.若四边形MNQP的面积为3,则k的值为( )
A.9 B.12
C.15 D.18
10. (2020·昆明)在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有( )
A.4个 B.5个 C.6个 D.7个
二、填空题
11. (2019?郴州)若,则__________.
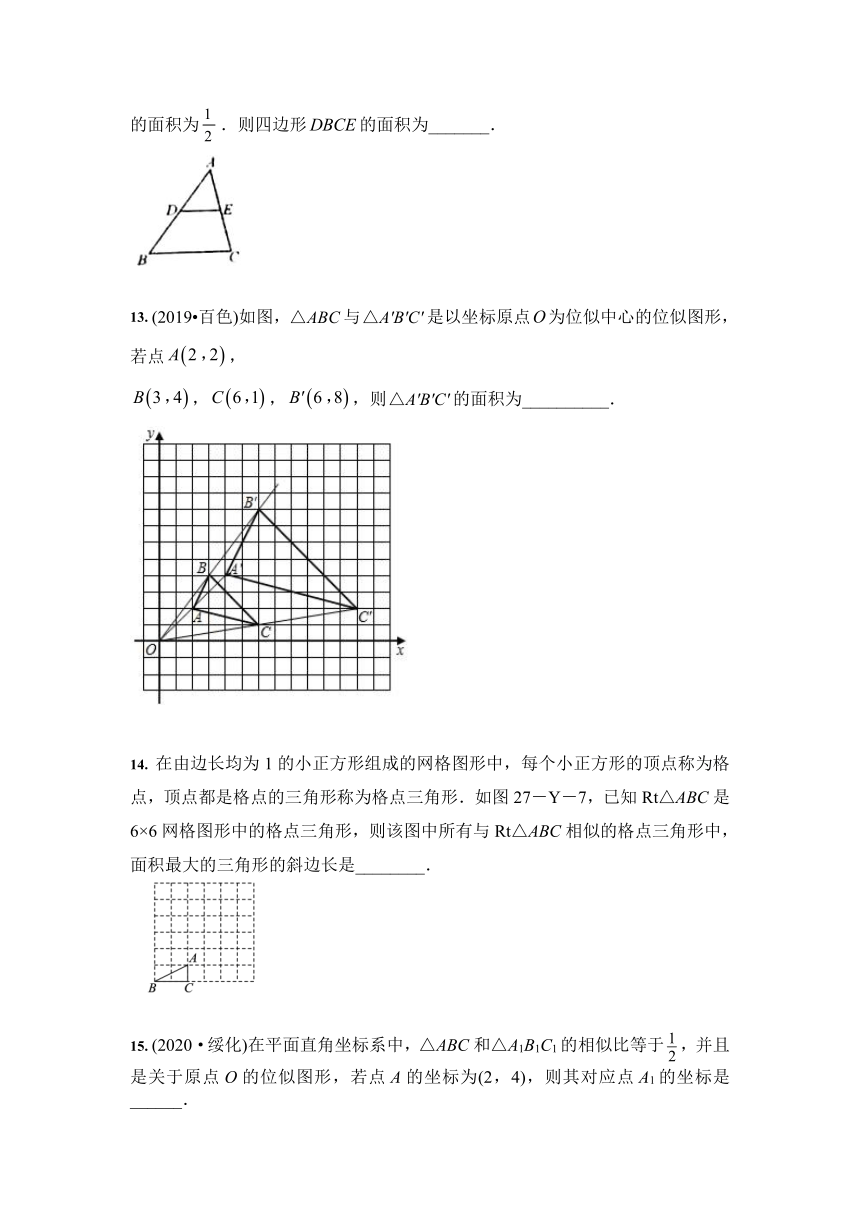
12. (2020·吉林)如图,在中,,分别是边,的中点.若的面积为.则四边形的面积为_______.
13. (2019?百色)如图,与是以坐标原点为位似中心的位似图形,若点,
,,,则的面积为__________.
14. 在由边长均为1的小正方形组成的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图27-Y-7,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是________.
15. (2020·绥化)在平面直角坐标系中,△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,若点A的坐标为(2,4),则其对应点A1的坐标是______.
16. 如图,在矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE,BD交于点P,过点P作PQ⊥BC于点Q,则PQ=________.
17. 在平面直角坐标系中,点A关于y轴的对称点为点B,点A关于原点O的对称点为点C.
(1)若点A的坐标为(1,2),请你在给出的坐标系中画出△ABC.设AB与y轴的交点为D,则=__________;
(2)若点A的坐标为(a,b)(ab≠0),则△ABC的形状为____________.
18. 如图,直线y=-x-3交x轴于点A,交y轴于点B,P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是________________.
19. (2019?辽阳)如图,平面直角坐标系中,矩形的边分别在轴,轴上,点的坐标为,点在矩形的内部,点在边上,满足∽,当是等腰三角形时,点坐标为__________.
20. (2019?泸州)如图,在等腰中,,,点在边上,,点在边上,,垂足为,则长为__________.
三、解答题
21. 在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°),得到△A′B′C.
(1)如图①,当AB∥CB′时,设A′B′与CB相交于点D.证明:△A′CD是等边三角形;
(2)如图②,连接A′A、B′B,设△ACA′和△BCB′的面积分别为S△ACA′和S△BCB′.求证:S△ACA′∶S△BCB′=1∶3;
(3)如图③,设AC中点为E,A′B′中点为P,AC=a,连接EP,当θ=________°时,EP长度最大,最大值为________.
图① 图② 图③
22. (2019?广东)如图,在中,点是边上的一点.
(1)请用尺规作图法,在内,求作,使,交于;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,若,求的值.
23. (2019?菏泽)如图,和是有公共顶点的等腰直角三角形,.
(1)如图1,连接,,的廷长线交于点,交于点,求证:;
(2)如图2,把绕点顺时针旋转,当点落在上时,连接,,的延长线交于点,若,,求的面积.
24. (2020·江苏徐州)我们知道:如图①,点B把线段AC分成两部分,如果,那么称点B为线段AC的黄金分割点.它们的比值为.
(1)在图①中,若AC=20cm,则AB的长为 cm;
(2)如图②,用边长为20cm的正方形纸片进行如下操作:对折正方形ABCD得折痕EF,连接CE,将CB折叠到CE上,点B的对应点H,得折痕CG.试说明:G是AB的黄金分割点;
(3)如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E(AE>DE),连接BE,作CF⊥BE,交AB于点F,延长EF、CB交于点P.他发现当PB与BC满足某种关系时,E、F恰好分别是AD、AB的黄金分割点.请猜想小明的发现,并说明理由.
图① 图 ② 图③
25. 如图,已知△ABC∽△A1B1C1,相似比为k(k>1),且△ABC的三边长分别为a、b、c(a>b>c),△A1B1C1的三边长分别为a1、b1、c1.
(1)若c=a1,求证:a=kc;
(2)若c=a1,试给出符合条件的一对△ABC和△A1B1C1,使得a、b、c和a1、b1、c1都是正整数,并加以说明;
(3)若b=a1,c=b1,是否存在△ABC和△A1B1C1使得k=2?请说明理由.
人教版 九年级数学下册 第二十七章 相似 综合训练-答案
一、选择题
1. 【答案】A
2. 【答案】A
【解析】解析:连接AO并延长AO至点N,连接BO并延长PO至点P, 连接CO并延长CO至点M, 连接DO并延长DO至Q,可知,所以以点O为位似中心,四边形ABCD的位似图形是四边形NPMQ,故答案为A.
3. 【答案】B
【解析】A、如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9,是假命题;
B、如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9,是真命题;
C、如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为16∶81,是假命题;
D、如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为16∶81,是假命题,
故选B.
4. 【答案】B
【解析】本题考查了在坐标系中,位似图形点的坐标.在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(–kx,–ky).由A(4,3),位似比k=,可得C()因此本题选B.
5. 【答案】B [解析] 依题意可知S△ADE=1,S△ABD=2,
∴S四边形ABDE=3.
∵AB⊥AD,AD⊥DE,∴DE∥AB,
∴△EDC∽△ABC,∴=()2,即=()2,解得S△ABC=4.故选B.
6. 【答案】 B.
【解析】利用平行四边形的性质可得出点O为线段BD的中点,结合点E是CD的中点可得出线段OE为△DBC的中位线,利用三角形中位线定理可得出OE∥BC,OE=BC,进而可得出△DOE∽△DBC,再利用相似三角形的面积比等于相似比的平分,即可求出△DEO与△BCD的面积的比为1:4.
7. 【答案】B
【解析】∵,∴,
∴,即,解得:,故选B.
8. 【答案】C
【解析】∵四边形EFGH为正方形,∴∠EGH=45°,∠FGH=90°,∵OG=GP,∴∠GOP=∠OPG=67.5°,∴∠PBG=22.5°,又∵∠DBC=45°,∴∠GBC=22.5°,∴∠PBG=∠GBC,
∵∠BGP=∠BG=90°,BG=BG,∴△BPG≌△BCG,∴PG=CG.设OG=PG=CG=x,
∵O为EG,BD的交点,∴EG=2x,FGx.∵四个全等的直角三角形拼成“赵爽弦图”,∴BF=CG=x,
∴BG=xx,∴BC2=BG2+CG2,
∴,因此本题选D.
9. 【答案】D [解析] ∵NQ∥MP∥OB,∴△ANQ∽△AMP∽△AOB.∵M,N是OA的三等分点,∴=,=,∴=.
∵四边形MNQP的面积为3,
∴=,∴S△ANQ=1.
∵=()2=,∴S△AOB=9,
∴k=2S△AOB=18.
10. 【答案】A
【解析】本题考查了相似三角形的判定.符合条件的三角形有四个,如图所示:
因此本题选A.
二、填空题
11. 【答案】
【解析】∵,∴,
故2y=x,则,故答案为:.
12. 【答案】
【解析】点,分别是边,的中点,
,即
又,
则四边形的面积为.
故答案为:.
13. 【答案】18
【解析】∵与是以坐标原点为位似中心的位似图形,
若点,,∴位似比为,
∵,,
∴,
∴的面积为:,
故答案为:18.
14. 【答案】5 [解析] ∵在Rt△ABC中,AC=1,BC=2,
∴AB=,AC∶BC=1∶2,
∴与Rt△ABC相似的格点三角形的两直角边的比值为1∶2.
若该三角形最短边长为4,则另一直角边长为8,但在6×6网格图形中,最长线段为6 ,∴画不出端点都在格点且长为8的线段,故最短直角边长应小于4.在图中尝试,可画出DE=,EF=2 ,DF=5 的格点三角形.
∵===,
∴△ABC∽△DFE,
∴∠DEF=∠C=90°,
∴此时△DEF的面积为×2 ÷2=10,△DEF为面积最大的三角形,其斜边长为5 .
15. 【答案】(-4,-8)或(4,8)
【解析】∵△ABC和△A1B1C1的相似比等于,∴△A1B1C1和△ABC的相似比等于2.因此将点A(2,4)的横、纵坐标乘以±2即得点A1的坐标,∴点A1的坐标是(-4,-8)或(4,8).
16. 【答案】 [解析] ∵四边形ABCD是矩形,
∴AB∥CD,AB=CD.
∵E为CD的中点,∴DE=CD=AB=1.
∵AB∥CD,∴△ABP∽△EDP,∴=,∴=,∴=.
∵PQ⊥BC,∴PQ∥CD,
∴△BPQ∽△BDC,∴==.
∵CD=2,∴PQ=.
17. 【答案】(1)△ABC如图 (2)直角三角形 解析:(1)因为点A的坐标为(1,2),所以点A关于y轴的对称点B的坐标为(-1,2),关于原点的对称点C的坐标为(-1,-2).连AB,BC,AC,作△ABC.
设AB交y轴于D点,如图,
D点坐标为(0,2),
∵OD∥BC,
∴△ADO∽△ABC.
∴==.
(2)∵ab≠0,∴a≠0,且b≠0,
∴点A不在坐标轴上,
∴AB∥x轴,BC⊥x轴.
∴∠ABC=90°.
∴△ABC是直角三角形.
18. 【答案】(-,0)或(-,0)[解析] 如图,依题意可知A(-4,0),B(0,-3),
∴OA=4,OB=3,
∴AB==5.
设⊙P与直线AB相切于点D,连接PD,则PD⊥AB,PD=1.
易得△APD∽△ABO,
∴=,即=,
∴AP=,∴OP=或OP=,
∴点P的坐标是(-,0)或(-,0).
19. 【答案】或
【解析】∵点在矩形的内部,且是等腰三角形,
∴点在的垂直平分线上或在以点为圆心为半径的圆弧上;
①当点在的垂直平分线上时,点同时在上,的垂直平分线与的交点即是,如图1所示,
∵,,
∴,
∴∽,
∵四边形是矩形,点的坐标为,
∴点横坐标为﹣4,,,,
∵∽,
∴,即,
解得:,
∴点.
②点在以点为圆心为半径的圆弧上,圆弧与的交点为,
过点作于,如图2所示,
∵,∴,
∴∽,
∵四边形是矩形,点的坐标为,
∴,,,
∴,∴,
∵∽,
∴,即:,
解得:,,
∴,
∴点,
综上所述:点的坐标为:或,
故答案为:或.
20. 【答案】
【解析】如图,过作于,则∠AHD=90°,
∵在等腰中,,,
∴,,
∴∠ADH=90°–∠CAD=45°=∠CAD,
∴,
∴CH=AC–AH=15–DH,
∵,∴,
又∵∠ANH=∠DNF,∴,
∴,∴,
∵,CE+BE=BC=15,∴,
∴,
∴,
∴,故答案为:.
三、解答题
21. 【答案】
(1)证:∵AB∥CB′,∴∠BCB′=∠ABC=30°,
∴∠ACA′=30°;又∵∠ACB=90°,
∴A′CD=60°,又∠CA′B′=∠CAB=60°.
∴△A′CD是等边三角形.
(2)证:∵AC=A′C,BC=B′C,∴= .
又∠ACA′=∠BCB′,∴△ACA′∽△BCB′.
∵=tan30°=,∴S△ACA′∶S△BCB′=AC2∶BC2=1∶3.
(3)120,.
22. 【答案】
(1)如图所示:
(2)∵,
∴.
∴.
23. 【答案】
(1)∵和是有公共顶点的等腰直角三角形,,
∴,,,
即,
在与中,,
∴,∴,
∵,
∴,∴.
(2)在与中,,
∴,
∴,,
∵,
∴,
∴,
∵,,
∴,,
∴,,
∵,
∴,
∴,
∴,,
∴,
∴的面积.
24. 【答案】
解: (1).解:∵,AC=20,∴AB=.
(2)延长CG交DA的延长线于点J,由折叠可知:∠BCG=∠ECG,
∵AD∥BC,∴∠J=∠BCG=∠ECG,∴JE=CE.由折叠可知:E、F为AD、BC的中点,∴DE=AE=10,
由勾股定理可得:CE=,∴EJ=,∴AJ=JE-AE=-10,
∵AJ∥BC,∴△AGJ∽△BGC,∴,∴G是AB的黄金分割点.
(3)PB=BC,理由如下:∵E为AD的黄金分割点,且AE>DE,∴AE=a.
∵CF⊥BE,∴∠ABE+∠CBE=∠CBE+∠BCF=90?,∴∠ABE=∠FCB,
在△BEA和△CFB中,∵,∴△BEA≌△CFB,∴BF=AE=a.
∴,∵AE∥BP,∴△AEF∽△BPF,∴,
∵AE=BF,∴PB=AB,∴PB=BC.
25. 【答案】
(1)证明:∵△ABC∽△A1B1C1,且相似比为k(k>1),
∴=k.∴a=ka1,又∵c=a1,∴a=kc.
(2)解:取a=8,b=6,c=4,同时取a1=4,b1=3,c1=2.
此时===2,∴△ABC∽△A1B1C1且c=a1.
(3)解:不存在这样的△ABC和△A1B1C1.理由如下:
若k=2,则a=2a1,b=2b1,c=2c1.
又∵b=a1,c=b1,
∴a=2a1=2b=4b1=4c,
∴b=2c.(12分)
∴b+c=2c+c<4c=a,与b+c>a矛盾,
故不存在这样的△ABC和△A1B1C1,使得k=2.
一、选择题
1. 2020·绍兴如图,三角尺在灯光照射下形成投影,三角尺与其投影的相似比为2∶5,且三角尺的一边长为8 cm,则投影三角尺的对应边长为( )
A.20 cm B.10 cm C.8 cm D.3.2 cm
2. (2020·河北) 在图5所示的网格中,以点O为位似中心,四边形ABCD的位似图形是
A.四边形NPMQ B.四边形NPMR
C.四边形NHMQ D.四边形NHMR
3. (2019?重庆)下列命题是真命题的是
A.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为2∶3
B.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9
C.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为2∶3
D.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为4∶9
4. (2020·嘉兴) 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点C坐标为( )
A.(﹣1,﹣1) B.() C.() D.(﹣2,﹣1)
5. 如图,在△ABC中,D为BC边上的一点,且AD=AB=2,AD⊥AB.过点D作DE⊥AD,交AC于点E.若DE=1,则△ABC的面积为( )
图27-Y-3
A.4 B.4
C.2 D.8
6. (2020·云南)如图,平行四边形ABCD的对角线AC,BD相交于点O,E是CD的中点.则△DEO与△BCD的面积的比等于( )
A. B. C. D.
7. (2019?贺州)如图,在中,分别是边上的点,,若,则等于
A.5 B.6
C.7 D.8
8. (2020?丽水)如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH.连结EG,BD相交于点O、BD与HC相交于点P.若GO=GP,则的值是( )
A.1 B.2 C.5 D.
9. 如图,△ABO的顶点A在反比例函数y=(x>0)的图象上,∠ABO=90°,过AO边的三等分点M,N分别作x轴的平行线交AB于点P,Q.若四边形MNQP的面积为3,则k的值为( )
A.9 B.12
C.15 D.18
10. (2020·昆明)在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有( )
A.4个 B.5个 C.6个 D.7个
二、填空题
11. (2019?郴州)若,则__________.
12. (2020·吉林)如图,在中,,分别是边,的中点.若的面积为.则四边形的面积为_______.
13. (2019?百色)如图,与是以坐标原点为位似中心的位似图形,若点,
,,,则的面积为__________.
14. 在由边长均为1的小正方形组成的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图27-Y-7,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是________.
15. (2020·绥化)在平面直角坐标系中,△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,若点A的坐标为(2,4),则其对应点A1的坐标是______.
16. 如图,在矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE,BD交于点P,过点P作PQ⊥BC于点Q,则PQ=________.
17. 在平面直角坐标系中,点A关于y轴的对称点为点B,点A关于原点O的对称点为点C.
(1)若点A的坐标为(1,2),请你在给出的坐标系中画出△ABC.设AB与y轴的交点为D,则=__________;
(2)若点A的坐标为(a,b)(ab≠0),则△ABC的形状为____________.
18. 如图,直线y=-x-3交x轴于点A,交y轴于点B,P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是________________.
19. (2019?辽阳)如图,平面直角坐标系中,矩形的边分别在轴,轴上,点的坐标为,点在矩形的内部,点在边上,满足∽,当是等腰三角形时,点坐标为__________.
20. (2019?泸州)如图,在等腰中,,,点在边上,,点在边上,,垂足为,则长为__________.
三、解答题
21. 在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°),得到△A′B′C.
(1)如图①,当AB∥CB′时,设A′B′与CB相交于点D.证明:△A′CD是等边三角形;
(2)如图②,连接A′A、B′B,设△ACA′和△BCB′的面积分别为S△ACA′和S△BCB′.求证:S△ACA′∶S△BCB′=1∶3;
(3)如图③,设AC中点为E,A′B′中点为P,AC=a,连接EP,当θ=________°时,EP长度最大,最大值为________.
图① 图② 图③
22. (2019?广东)如图,在中,点是边上的一点.
(1)请用尺规作图法,在内,求作,使,交于;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,若,求的值.
23. (2019?菏泽)如图,和是有公共顶点的等腰直角三角形,.
(1)如图1,连接,,的廷长线交于点,交于点,求证:;
(2)如图2,把绕点顺时针旋转,当点落在上时,连接,,的延长线交于点,若,,求的面积.
24. (2020·江苏徐州)我们知道:如图①,点B把线段AC分成两部分,如果,那么称点B为线段AC的黄金分割点.它们的比值为.
(1)在图①中,若AC=20cm,则AB的长为 cm;
(2)如图②,用边长为20cm的正方形纸片进行如下操作:对折正方形ABCD得折痕EF,连接CE,将CB折叠到CE上,点B的对应点H,得折痕CG.试说明:G是AB的黄金分割点;
(3)如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E(AE>DE),连接BE,作CF⊥BE,交AB于点F,延长EF、CB交于点P.他发现当PB与BC满足某种关系时,E、F恰好分别是AD、AB的黄金分割点.请猜想小明的发现,并说明理由.
图① 图 ② 图③
25. 如图,已知△ABC∽△A1B1C1,相似比为k(k>1),且△ABC的三边长分别为a、b、c(a>b>c),△A1B1C1的三边长分别为a1、b1、c1.
(1)若c=a1,求证:a=kc;
(2)若c=a1,试给出符合条件的一对△ABC和△A1B1C1,使得a、b、c和a1、b1、c1都是正整数,并加以说明;
(3)若b=a1,c=b1,是否存在△ABC和△A1B1C1使得k=2?请说明理由.
人教版 九年级数学下册 第二十七章 相似 综合训练-答案
一、选择题
1. 【答案】A
2. 【答案】A
【解析】解析:连接AO并延长AO至点N,连接BO并延长PO至点P, 连接CO并延长CO至点M, 连接DO并延长DO至Q,可知,所以以点O为位似中心,四边形ABCD的位似图形是四边形NPMQ,故答案为A.
3. 【答案】B
【解析】A、如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9,是假命题;
B、如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9,是真命题;
C、如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为16∶81,是假命题;
D、如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为16∶81,是假命题,
故选B.
4. 【答案】B
【解析】本题考查了在坐标系中,位似图形点的坐标.在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(–kx,–ky).由A(4,3),位似比k=,可得C()因此本题选B.
5. 【答案】B [解析] 依题意可知S△ADE=1,S△ABD=2,
∴S四边形ABDE=3.
∵AB⊥AD,AD⊥DE,∴DE∥AB,
∴△EDC∽△ABC,∴=()2,即=()2,解得S△ABC=4.故选B.
6. 【答案】 B.
【解析】利用平行四边形的性质可得出点O为线段BD的中点,结合点E是CD的中点可得出线段OE为△DBC的中位线,利用三角形中位线定理可得出OE∥BC,OE=BC,进而可得出△DOE∽△DBC,再利用相似三角形的面积比等于相似比的平分,即可求出△DEO与△BCD的面积的比为1:4.
7. 【答案】B
【解析】∵,∴,
∴,即,解得:,故选B.
8. 【答案】C
【解析】∵四边形EFGH为正方形,∴∠EGH=45°,∠FGH=90°,∵OG=GP,∴∠GOP=∠OPG=67.5°,∴∠PBG=22.5°,又∵∠DBC=45°,∴∠GBC=22.5°,∴∠PBG=∠GBC,
∵∠BGP=∠BG=90°,BG=BG,∴△BPG≌△BCG,∴PG=CG.设OG=PG=CG=x,
∵O为EG,BD的交点,∴EG=2x,FGx.∵四个全等的直角三角形拼成“赵爽弦图”,∴BF=CG=x,
∴BG=xx,∴BC2=BG2+CG2,
∴,因此本题选D.
9. 【答案】D [解析] ∵NQ∥MP∥OB,∴△ANQ∽△AMP∽△AOB.∵M,N是OA的三等分点,∴=,=,∴=.
∵四边形MNQP的面积为3,
∴=,∴S△ANQ=1.
∵=()2=,∴S△AOB=9,
∴k=2S△AOB=18.
10. 【答案】A
【解析】本题考查了相似三角形的判定.符合条件的三角形有四个,如图所示:
因此本题选A.
二、填空题
11. 【答案】
【解析】∵,∴,
故2y=x,则,故答案为:.
12. 【答案】
【解析】点,分别是边,的中点,
,即
又,
则四边形的面积为.
故答案为:.
13. 【答案】18
【解析】∵与是以坐标原点为位似中心的位似图形,
若点,,∴位似比为,
∵,,
∴,
∴的面积为:,
故答案为:18.
14. 【答案】5 [解析] ∵在Rt△ABC中,AC=1,BC=2,
∴AB=,AC∶BC=1∶2,
∴与Rt△ABC相似的格点三角形的两直角边的比值为1∶2.
若该三角形最短边长为4,则另一直角边长为8,但在6×6网格图形中,最长线段为6 ,∴画不出端点都在格点且长为8的线段,故最短直角边长应小于4.在图中尝试,可画出DE=,EF=2 ,DF=5 的格点三角形.
∵===,
∴△ABC∽△DFE,
∴∠DEF=∠C=90°,
∴此时△DEF的面积为×2 ÷2=10,△DEF为面积最大的三角形,其斜边长为5 .
15. 【答案】(-4,-8)或(4,8)
【解析】∵△ABC和△A1B1C1的相似比等于,∴△A1B1C1和△ABC的相似比等于2.因此将点A(2,4)的横、纵坐标乘以±2即得点A1的坐标,∴点A1的坐标是(-4,-8)或(4,8).
16. 【答案】 [解析] ∵四边形ABCD是矩形,
∴AB∥CD,AB=CD.
∵E为CD的中点,∴DE=CD=AB=1.
∵AB∥CD,∴△ABP∽△EDP,∴=,∴=,∴=.
∵PQ⊥BC,∴PQ∥CD,
∴△BPQ∽△BDC,∴==.
∵CD=2,∴PQ=.
17. 【答案】(1)△ABC如图 (2)直角三角形 解析:(1)因为点A的坐标为(1,2),所以点A关于y轴的对称点B的坐标为(-1,2),关于原点的对称点C的坐标为(-1,-2).连AB,BC,AC,作△ABC.
设AB交y轴于D点,如图,
D点坐标为(0,2),
∵OD∥BC,
∴△ADO∽△ABC.
∴==.
(2)∵ab≠0,∴a≠0,且b≠0,
∴点A不在坐标轴上,
∴AB∥x轴,BC⊥x轴.
∴∠ABC=90°.
∴△ABC是直角三角形.
18. 【答案】(-,0)或(-,0)[解析] 如图,依题意可知A(-4,0),B(0,-3),
∴OA=4,OB=3,
∴AB==5.
设⊙P与直线AB相切于点D,连接PD,则PD⊥AB,PD=1.
易得△APD∽△ABO,
∴=,即=,
∴AP=,∴OP=或OP=,
∴点P的坐标是(-,0)或(-,0).
19. 【答案】或
【解析】∵点在矩形的内部,且是等腰三角形,
∴点在的垂直平分线上或在以点为圆心为半径的圆弧上;
①当点在的垂直平分线上时,点同时在上,的垂直平分线与的交点即是,如图1所示,
∵,,
∴,
∴∽,
∵四边形是矩形,点的坐标为,
∴点横坐标为﹣4,,,,
∵∽,
∴,即,
解得:,
∴点.
②点在以点为圆心为半径的圆弧上,圆弧与的交点为,
过点作于,如图2所示,
∵,∴,
∴∽,
∵四边形是矩形,点的坐标为,
∴,,,
∴,∴,
∵∽,
∴,即:,
解得:,,
∴,
∴点,
综上所述:点的坐标为:或,
故答案为:或.
20. 【答案】
【解析】如图,过作于,则∠AHD=90°,
∵在等腰中,,,
∴,,
∴∠ADH=90°–∠CAD=45°=∠CAD,
∴,
∴CH=AC–AH=15–DH,
∵,∴,
又∵∠ANH=∠DNF,∴,
∴,∴,
∵,CE+BE=BC=15,∴,
∴,
∴,
∴,故答案为:.
三、解答题
21. 【答案】
(1)证:∵AB∥CB′,∴∠BCB′=∠ABC=30°,
∴∠ACA′=30°;又∵∠ACB=90°,
∴A′CD=60°,又∠CA′B′=∠CAB=60°.
∴△A′CD是等边三角形.
(2)证:∵AC=A′C,BC=B′C,∴= .
又∠ACA′=∠BCB′,∴△ACA′∽△BCB′.
∵=tan30°=,∴S△ACA′∶S△BCB′=AC2∶BC2=1∶3.
(3)120,.
22. 【答案】
(1)如图所示:
(2)∵,
∴.
∴.
23. 【答案】
(1)∵和是有公共顶点的等腰直角三角形,,
∴,,,
即,
在与中,,
∴,∴,
∵,
∴,∴.
(2)在与中,,
∴,
∴,,
∵,
∴,
∴,
∵,,
∴,,
∴,,
∵,
∴,
∴,
∴,,
∴,
∴的面积.
24. 【答案】
解: (1).解:∵,AC=20,∴AB=.
(2)延长CG交DA的延长线于点J,由折叠可知:∠BCG=∠ECG,
∵AD∥BC,∴∠J=∠BCG=∠ECG,∴JE=CE.由折叠可知:E、F为AD、BC的中点,∴DE=AE=10,
由勾股定理可得:CE=,∴EJ=,∴AJ=JE-AE=-10,
∵AJ∥BC,∴△AGJ∽△BGC,∴,∴G是AB的黄金分割点.
(3)PB=BC,理由如下:∵E为AD的黄金分割点,且AE>DE,∴AE=a.
∵CF⊥BE,∴∠ABE+∠CBE=∠CBE+∠BCF=90?,∴∠ABE=∠FCB,
在△BEA和△CFB中,∵,∴△BEA≌△CFB,∴BF=AE=a.
∴,∵AE∥BP,∴△AEF∽△BPF,∴,
∵AE=BF,∴PB=AB,∴PB=BC.
25. 【答案】
(1)证明:∵△ABC∽△A1B1C1,且相似比为k(k>1),
∴=k.∴a=ka1,又∵c=a1,∴a=kc.
(2)解:取a=8,b=6,c=4,同时取a1=4,b1=3,c1=2.
此时===2,∴△ABC∽△A1B1C1且c=a1.
(3)解:不存在这样的△ABC和△A1B1C1.理由如下:
若k=2,则a=2a1,b=2b1,c=2c1.
又∵b=a1,c=b1,
∴a=2a1=2b=4b1=4c,
∴b=2c.(12分)
∴b+c=2c+c<4c=a,与b+c>a矛盾,
故不存在这样的△ABC和△A1B1C1,使得k=2.
