9.2单项式乘多项式学案(苏科版七年级下)
文档属性
| 名称 | 9.2单项式乘多项式学案(苏科版七年级下) |

|
|
| 格式 | zip | ||
| 文件大小 | 40.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-27 00:00:00 | ||
图片预览

文档简介
9.2 单项式乘多项式
主备:蒋剑群 审核:初一数学备课组
班级 姓名
学习目标:1、知道利用乘法分配律可以将单项式乘多项式转化成单项式乘单项式;
2、会进行单项式乘多项式的运算;
3、经历探索单项式乘多项式法则的过程,发展有条理的思考及语言表达能力。
【课前准备】:
课前要求学生制作边长分别为、,、,、的长方形,课堂上由学生动手拼成大长方形,计算拼成的图形面积并交流做法。
让学生在交流的基础上思考下列问题:
(1)有哪些方法计算大长方形的面积?试分别用代数式表示出来。
(2)根据以上探索你认为应如何进行单项式与多项式的乘法运算?
通过探索得:进而得出单项式乘多项式法则
【探索新知】
单项式与多项式相乘,
法则说明:1、分清多项式的各项。
2、为避免符号出错,所得结果应先用加号连接,再进行化简。
【知识运用】
例1:计算(1) ; (2)
计算:
(1) a (2a-3) (2) a2 (1-3a) (3) 3x(x2-2x-1)
(4) -2x2y(3x2-2x-3) (5) (2x2-3xy+4y2)(-2xy)
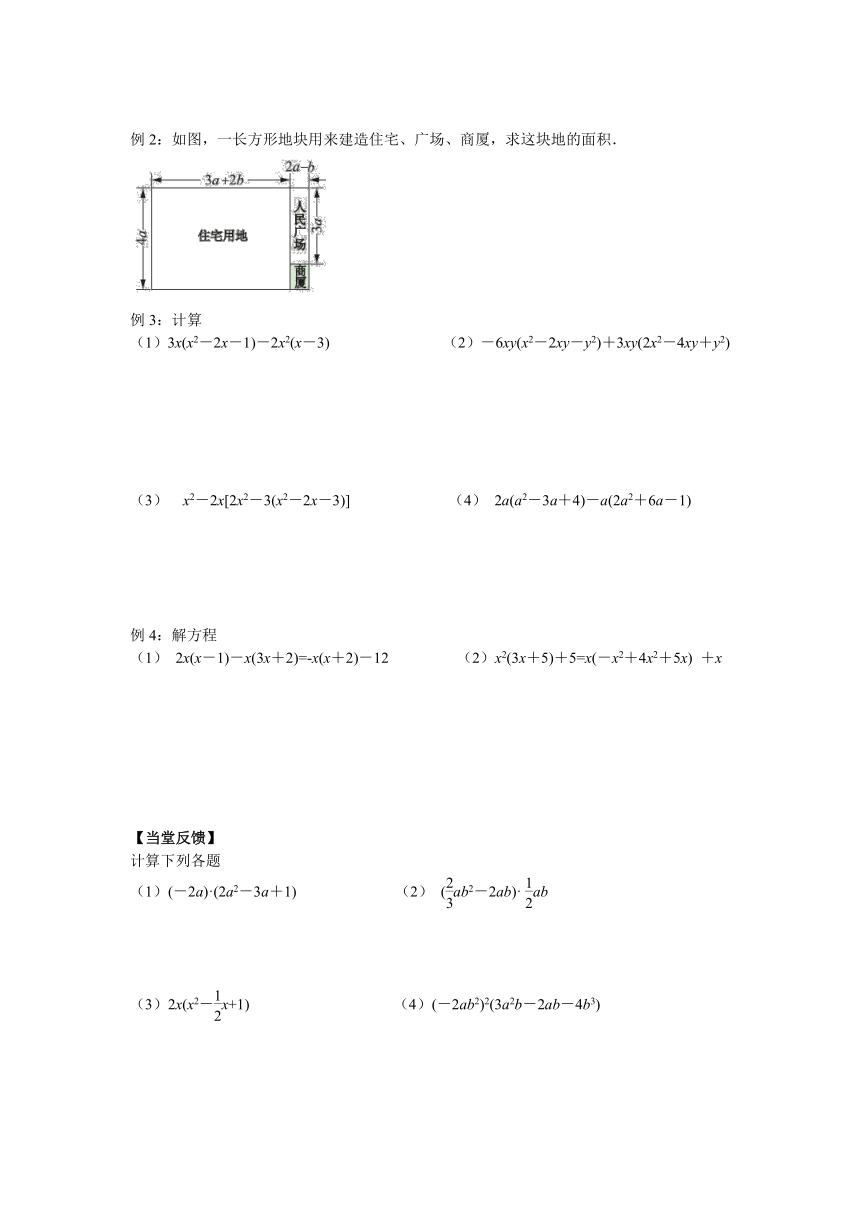
例2:如图,一长方形地块用来建造住宅、广场、商厦,求这块地的面积.
例3:计算
(1)3x(x2-2x-1)-2x2(x-3) (2)-6xy(x2-2xy-y2)+3xy(2x2-4xy+y2)
(3) x2-2x[2x2-3(x2-2x-3)] (4) 2a(a2-3a+4)-a(2a2+6a-1)
例4:解方程
(1) 2x(x-1)-x(3x+2)=-x(x+2)-12 (2)x2(3x+5)+5=x(-x2+4x2+5x) +x
【当堂反馈】
计算下列各题
(1)(-2a)·(2a2-3a+1) (2) (ab2-2ab)· ab
(3)2x(x2-x+1) (4)(-2ab2)2(3a2b-2ab-4b3)
(5) 3x2·(-3xy)2-x2(x2y2-2x) (6)2a· (a2+3a-2)-3(a3+2a2-a+1)
课后巩固
一.选择:
1.下列运算中不正确的是 ( )
A.3xy-(x2-2xy)=5xy-x2 B.5x(2x2-y)=10x3-5xy
C.5mn(2m+3n-1)=10m2n+15mn2-1 D.(ab)2(2ab2-c)=2a3b4-a2b2c
2.-a2(a-b+c)与a(a2-ab+ac)的关系是 ( )
A.相等 B.互为相反数 C.前者是后者的-a倍 D.以上结果都不对
二.计算下列各题
(1)(-2x)2(x2-x+1) (2)5a(a2-3a+1)-a2(1-a)
(3)2m2-n(5m-n)-m(2m-5n) (4)-5x2(-2xy)2-x2(7x2y2-2x)
三.如图,把一张边长为xcm的正方形纸板的四个角各剪去一个边长为ycm的小正方形,然后把它折成一个无盖纸盒,求纸盒的四个侧面的面积之和(结果用关于x、y的代数式表示).
四.先化简,再求值:x2(x2-x+1)-x(x3-x2+x-1),其中 x=
思考:
阅读:已知x2y=3,求2xy(x5y2-3x3y-4x)的值.
分析:考虑到x、y的可能值较多,不能逐一代入求解,故考虑整体思想,将x2y=3整体代入.
解:2xy(x5y2-3x3y-4x)=2x6y3-6x4y2-8x2y
=2(x2y)3-6(x2y)2-8x2y
=2×33-6×32-8×3=-24
你能用上述方法解决以下问题吗?试一试!
已知ab=3,求(2a3b2-3a2b+4a)·(-2b)的值.
【课后作业】
1.下列运算中不正确的是 ( )
A.3xy-(x2-2xy)=5xy-x2 B.5x(2x2-y)=10x3-5xy
C.5mn(2m+3n-1)=10m2n+15mn2-1 D.(ab)2(2ab2-c)=2a3b4-a2b2c
2.-a2(a-b+c)与a(a2-ab+ac)的关系是 ( )
A.相等 B.互为相反数 C.前者是后者的-a倍 D.以上结果都不对
3.填空题:
(1);
(2);
(3)当时,.
4.计算题: (1) (2)
(3) (4)
(5) (6)
(7) (8)
5. 解方程:
主备:蒋剑群 审核:初一数学备课组
班级 姓名
学习目标:1、知道利用乘法分配律可以将单项式乘多项式转化成单项式乘单项式;
2、会进行单项式乘多项式的运算;
3、经历探索单项式乘多项式法则的过程,发展有条理的思考及语言表达能力。
【课前准备】:
课前要求学生制作边长分别为、,、,、的长方形,课堂上由学生动手拼成大长方形,计算拼成的图形面积并交流做法。
让学生在交流的基础上思考下列问题:
(1)有哪些方法计算大长方形的面积?试分别用代数式表示出来。
(2)根据以上探索你认为应如何进行单项式与多项式的乘法运算?
通过探索得:进而得出单项式乘多项式法则
【探索新知】
单项式与多项式相乘,
法则说明:1、分清多项式的各项。
2、为避免符号出错,所得结果应先用加号连接,再进行化简。
【知识运用】
例1:计算(1) ; (2)
计算:
(1) a (2a-3) (2) a2 (1-3a) (3) 3x(x2-2x-1)
(4) -2x2y(3x2-2x-3) (5) (2x2-3xy+4y2)(-2xy)
例2:如图,一长方形地块用来建造住宅、广场、商厦,求这块地的面积.
例3:计算
(1)3x(x2-2x-1)-2x2(x-3) (2)-6xy(x2-2xy-y2)+3xy(2x2-4xy+y2)
(3) x2-2x[2x2-3(x2-2x-3)] (4) 2a(a2-3a+4)-a(2a2+6a-1)
例4:解方程
(1) 2x(x-1)-x(3x+2)=-x(x+2)-12 (2)x2(3x+5)+5=x(-x2+4x2+5x) +x
【当堂反馈】
计算下列各题
(1)(-2a)·(2a2-3a+1) (2) (ab2-2ab)· ab
(3)2x(x2-x+1) (4)(-2ab2)2(3a2b-2ab-4b3)
(5) 3x2·(-3xy)2-x2(x2y2-2x) (6)2a· (a2+3a-2)-3(a3+2a2-a+1)
课后巩固
一.选择:
1.下列运算中不正确的是 ( )
A.3xy-(x2-2xy)=5xy-x2 B.5x(2x2-y)=10x3-5xy
C.5mn(2m+3n-1)=10m2n+15mn2-1 D.(ab)2(2ab2-c)=2a3b4-a2b2c
2.-a2(a-b+c)与a(a2-ab+ac)的关系是 ( )
A.相等 B.互为相反数 C.前者是后者的-a倍 D.以上结果都不对
二.计算下列各题
(1)(-2x)2(x2-x+1) (2)5a(a2-3a+1)-a2(1-a)
(3)2m2-n(5m-n)-m(2m-5n) (4)-5x2(-2xy)2-x2(7x2y2-2x)
三.如图,把一张边长为xcm的正方形纸板的四个角各剪去一个边长为ycm的小正方形,然后把它折成一个无盖纸盒,求纸盒的四个侧面的面积之和(结果用关于x、y的代数式表示).
四.先化简,再求值:x2(x2-x+1)-x(x3-x2+x-1),其中 x=
思考:
阅读:已知x2y=3,求2xy(x5y2-3x3y-4x)的值.
分析:考虑到x、y的可能值较多,不能逐一代入求解,故考虑整体思想,将x2y=3整体代入.
解:2xy(x5y2-3x3y-4x)=2x6y3-6x4y2-8x2y
=2(x2y)3-6(x2y)2-8x2y
=2×33-6×32-8×3=-24
你能用上述方法解决以下问题吗?试一试!
已知ab=3,求(2a3b2-3a2b+4a)·(-2b)的值.
【课后作业】
1.下列运算中不正确的是 ( )
A.3xy-(x2-2xy)=5xy-x2 B.5x(2x2-y)=10x3-5xy
C.5mn(2m+3n-1)=10m2n+15mn2-1 D.(ab)2(2ab2-c)=2a3b4-a2b2c
2.-a2(a-b+c)与a(a2-ab+ac)的关系是 ( )
A.相等 B.互为相反数 C.前者是后者的-a倍 D.以上结果都不对
3.填空题:
(1);
(2);
(3)当时,.
4.计算题: (1) (2)
(3) (4)
(5) (6)
(7) (8)
5. 解方程:
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
