2020-2021学年冀教版数学九年级下册第一次月考测试题(word版含答案)
文档属性
| 名称 | 2020-2021学年冀教版数学九年级下册第一次月考测试题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-21 11:09:15 | ||
图片预览



文档简介
冀教版数学九年级下册第一次月考测试题及答案
(适用于第29章和第30章)
(时间:90分钟
分值:100分)
一、选择题(每小题4分,共40分)
1.将y=x2向上平移2个单位后所得到的抛物线的解析式为(??
)
A.?y=x2﹣2?
B.?y=x2+2??
C.?y=(x﹣2)2?
D.?y=(x+2)2
2.如图29-Z-1所示,PA是⊙O的切线,切点为A,PA=2
,∠APO=30°,则⊙O的半径长为( )
A.4
B.2
C.2
D.3
图29-Z-1
图29-Z-2
3.如图29-Z-2,两个同心圆的半径分别为4
cm和5
cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
A.3
cm
B.4
cm
C.6
cm
D.8
cm
4.如图29-Z-3,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若
∠BCD=50°,则∠AOC的度数为( )
图29-Z-3
A.40°
B.50°
C.80°
D.100°
5.二次函数y=ax2+bx+c与一次函数y=ax+c,它们在同一直角坐标系中的图象大致是(?
)
A.????B.???
C.?????D.?
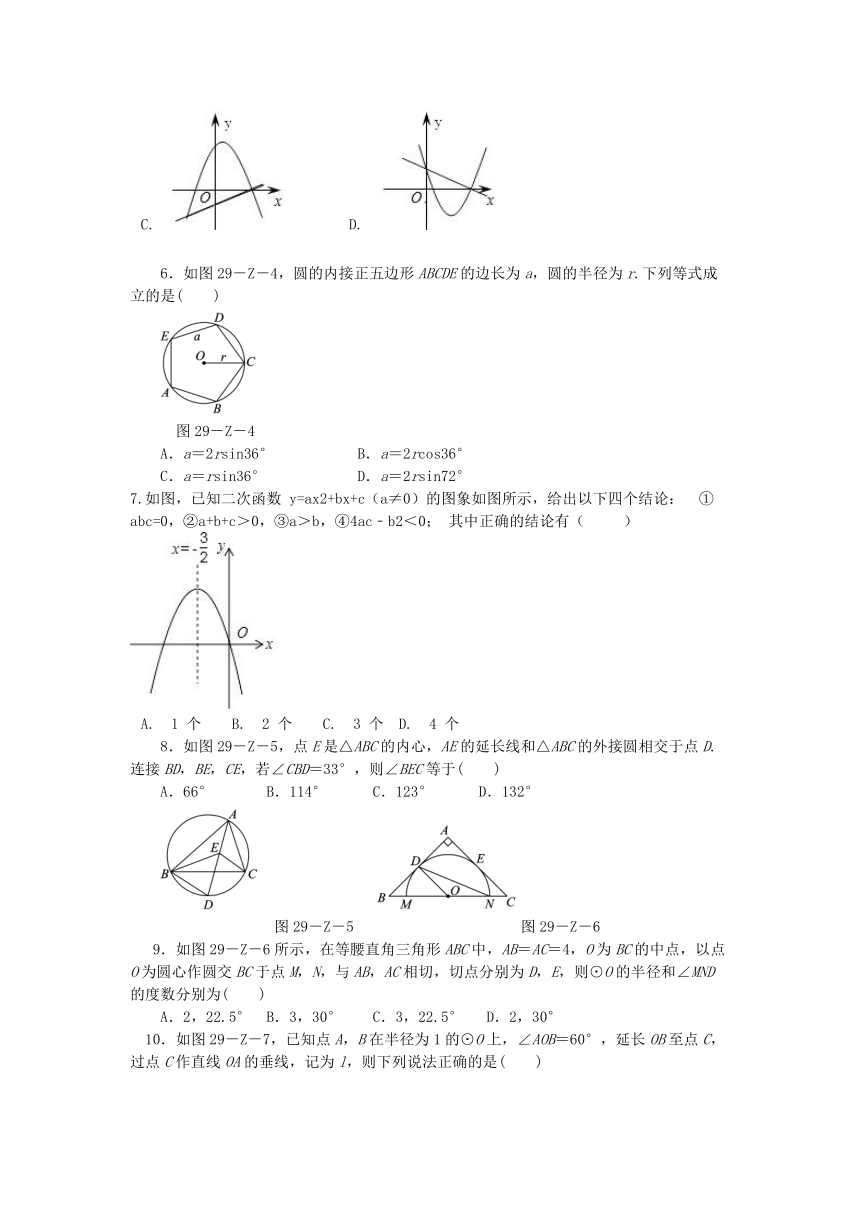
6.如图29-Z-4,圆的内接正五边形ABCDE的边长为a,圆的半径为r.下列等式成立的是( )
图29-Z-4
A.a=2rsin36°
B.a=2rcos36°
C.a=rsin36°
D.a=2rsin72°
7.如图,已知二次函数
y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:
①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;
其中正确的结论有(??
)
A.?1
个??B.?2
个??C.?3
个?D.?4
个
8.如图29-Z-5,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.连接BD,BE,CE,若∠CBD=33°,则∠BEC等于( )
A.66°
B.114°
C.123°
D.132°
图29-Z-5
图29-Z-6
9.如图29-Z-6所示,在等腰直角三角形ABC中,AB=AC=4,O为BC的中点,以点O为圆心作圆交BC于点M,N,与AB,AC相切,切点分别为D,E,则⊙O的半径和∠MND的度数分别为( )
A.2,22.5°
B.3,30°
C.3,22.5°
D.2,30°
10.如图29-Z-7,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至点C,过点C作直线OA的垂线,记为l,则下列说法正确的是( )
图29-Z-7
A.当BC等于0.5时,l与⊙O相离
B.当BC等于2时,l与⊙O相切
C.当BC等于1时,l与⊙O相交
D.当BC不为1时,l与⊙O不相切
二、填空题(每小题4分,共24分)
11.抛物线y=(x﹣2)2+1的顶点坐标是________.
12.二次函数y=x2+4x﹣3中,当x=﹣1时,y的值是________.
图29-Z-8
13.如图29-Z-8,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为________.
图29-Z-9
14.如图29-Z-9,PA与⊙O相切于点A,弦AB⊥OP,垂足为C,OP与⊙O相交于点D,已知OA=2,OP=4,则弦AB的长为________.
15.某工厂计划为一批长方体形状的产品涂上油漆,长方体的长和宽相等,高比长多0.5m,若长方体的长和宽用x(m)表示,长方体需涂油漆的表面积S(m2)表示为________.
16.如图29-Z-10,⊙M与x轴相切于原点,平行于y轴的直线交⊙M于P,Q两点,点P在点Q的下方.若点P的坐标是(2,1),则圆心M的坐标是________.
图29-Z-10
三、解答题(共36分)
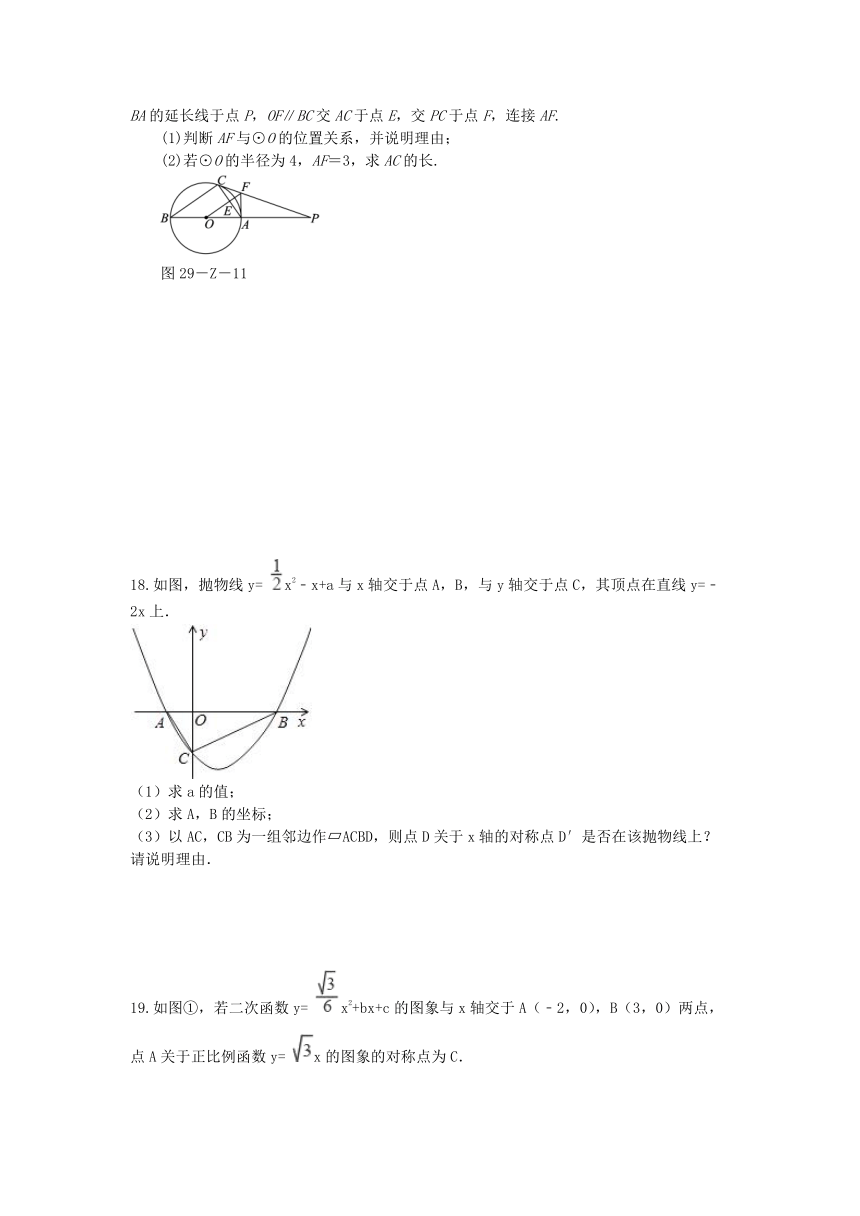
17.(10分)如图29-Z-11,△ABC内接于⊙O,AB是⊙O的直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.
(1)判断AF与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为4,AF=3,求AC的长.
图29-Z-11
18.如图,抛物线y=
x2﹣x+a与x轴交于点A,B,与y轴交于点C,其顶点在直线y=﹣2x上.
(1)求a的值;
(2)求A,B的坐标;
(3)以AC,CB为一组邻边作?ACBD,则点D关于x轴的对称点D′是否在该抛物线上?请说明理由.
19.如图①,若二次函数y=
x2+bx+c的图象与x轴交于A(﹣2,0),B(3,0)两点,点A关于正比例函数y=
x的图象的对称点为C.
(1)求b、c的值;
(2)证明:点C在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数y=
x的图象于点D,连结AC,交正比例函数y=
x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.
参考答案:
1.B
2.C [解析]
连接OA.因为PA是⊙O的切线,所以OA⊥PA,OA=AP·tan30°=2.
故选C.
3.C
4.C [解析]
∵在⊙O中,AB为直径,BC为弦,CD为切线,∴∠OCD=90°.
∵∠BCD=50°,∴∠OCB=40°,∴∠AOC=80°.
5. A
6.A [解析]
如图,作OF⊥BC于点F.∵∠COF=72°÷2=36°,∴CF=r·sin36°,∴a=2rsin36°.
7.C
8.C [解析]
在⊙O中,∵∠CBD=33°,∴∠CAD=33°.∵点E是△ABC的内心,∴∠BAC=66°,∴∠EBC+∠ECB=(180°-66°)=57°,
∴∠BEC=180°-57°=123°.故选C.
9.A [解析]
∵AB为⊙O的切线,
∴OD⊥AB,∴∠ODB=∠A=90°.
又∠B=∠B,∴△OBD∽△CBA,
∴==,
∴OD=CA=2,∠MND=∠DOB=∠C=22.5°.
故选A.
10.D [解析]
设直线l与OA的垂足为D.
A项,∵BC=0.5,
∴OC=OB+CB=1.5.
∵∠AOB=60°,
∴∠ACO=30°,∴DO=OC=0.75<1,
∴l与⊙O相交,故A项错误.
B项,∵BC=2,
∴OC=OB+CB=3.
∵∠AOB=60°,
∴∠ACO=30°,∴DO=OC=1.5>1,
∴l与⊙O相离,故B项错误.
C项,∵BC=1,∴OC=OB+CB=2.
∵∠AOB=60°,
∴∠ACO=30°,∴DO=OC=1,
∴l与⊙O相切,故C项错误.
D项,∵BC≠1,
∴OC=OB+CB≠2.
∵∠AOB=60°,
∴∠ACO=30°,
∴DO=OC≠1,
∴l与⊙O不相切,故D项正确.故选D.
11.
(2,1)
12.
﹣6
13. [解析]
如图,连接OE,OF,ON,OG.
∵四边形ABCD为矩形,
∴∠A=∠B=90°.
又∵AD,AB,BC分别与⊙O相切于E,F,G三点,
又∵OE=OF=OG,
∴∠AEO=∠AFO=∠OFB=∠BGO=90°.
∴四边形AFOE,FBGO是正方形,
∴AF=BF=AE=BG=2,∴DE=3.
∵DM是⊙O的切线,
∴DN=DE=3,MN=MG,
∴CM=5-2-MN=3-MN.
在Rt△DMC中,DM2=CD2+CM2,
∴(3+MN)2=42+(3-MN)2,
解得MN=,
∴DM=DN+MN=3+=.故答案为.
14.2
[解析]
∵PA与⊙O相切于点A,
∴OA⊥AP,
∴△POA是直角三角形.
∵OA=2,OP=4,即OP=2OA,
∴∠P=30°,∠O=60°.
则在Rt△AOC中,OC=OA=1,
从而AC=,∴AB=2
.故答案为2
.
15.S=6x2+2x
16.(0,2.5) [解析]
连接MP,过点P作PA⊥y轴于点A,设点M的坐标是(0,b),且b>0,
∵PA⊥y轴,∴∠PAM=90°,∴AP2+AM2=MP2,∴22+(b-1)2=b2,解得b=2.5,故答案是(0,2.5).
17.解:(1)AF与⊙O相切.
理由:如图,连接
OC.
∵PC为⊙O的切线,∴∠OCP=90°.
∵AB是⊙O的直径,∴∠BCA=90°.
∵OF∥BC,∴∠AEO=∠BCA=90°,
∴OF⊥AC.
∵OC=OA,∴∠COF=∠AOF,
又CO=AO,OF=OF,∴△OCF≌△OAF,
∴∠OAF=∠OCF=90°,
∴FA⊥OA.
∵点A在⊙O上,∴AF与⊙O相切.
(2)∵⊙O的半径为4,AF=3,FA⊥OA,∴在Rt△OFA中,OF==
=5.
∵FA⊥OA,OF⊥AC,易证△AOE∽△FOA,
∴=
,即=
,
解得AE=,∴AC=2AE=.
18.
(1)解:∵抛物线y=
x2﹣x+a其顶点在直线y=﹣2x上.
∴抛物线y=
x2﹣x+a,
=
(x2﹣2x)+a,
=
(x﹣1)2﹣
+a,
∴顶点坐标为:(1,﹣
+a),
∴y=﹣2x,﹣
+a=﹣2×1,
∴a=﹣
(2)解:二次函数解析式为:y=
x2﹣x﹣
,
∵抛物线y=
x2﹣x﹣
与x轴交于点A,B,
∴0=
x2﹣x﹣
,
整理得:x2﹣2x﹣3=0,
解得:x=﹣1或3,
A(﹣1,0),B(3,0)
(3)解:作出平行四边形ACBD,作DE⊥AB,
在△AOC和△BDE中
∵
∴△AOC≌△BED(AAS),
∵AO=1,
∴BE=1,
∵二次函数解析式为:y=
x2﹣x﹣
,
∴图象与y轴交点坐标为:(0,﹣
),
∴CO=
,∴DE=
,
D点的坐标为:(2,
),
∴点D关于x轴的对称点D′坐标为:(2,﹣
),
代入解析式y=
x2﹣x﹣
,
∵左边=﹣
,右边=
×4﹣2﹣
=﹣
,
∴D′点在函数图象上.
19.
(1)解:∵点A(﹣2,0),B(3,0)在抛物线y=
x2+bx+c上,
∴
,
解得:b=﹣
,c=﹣
(2)解:设点F在直线y=
x上,且F(2,
).
如答图1所示,过点F作FH⊥x轴于点H,则FH=
,OH=2,
∴tan∠FOB=
=
,∴∠FOB=60°.
∴∠AOE=∠FOB=60°.
连接OC,过点C作CK⊥x轴于点K.
∵点A、C关于y=
x对称,∴OC=OA=2,∠COE=∠AOE=60°.
∴∠COK=180°﹣∠AOE﹣∠COE=60°.
在Rt△COK中,CK=OC?sin60°=2×
=
,OK=OC?cos60°=2×
=1.
∴C(1,﹣
).
抛物线的解析式为:y=
x2﹣
x﹣
,当x=1时,y=﹣
,
∴点C在所求二次函数的图象上
(3)解:假设存在.
如答图1所示,在Rt△ACK中,由勾股定理得:AC=
=
=
.
如答图2所示,∵OB=3,∴BD=3
,AB=OA+OB=5.
在Rt△ABD中,由勾股定理得:AD=
=
=2
.
∵点A、C关于y=
x对称,
∴CD=AD=2
,∠DAC=∠DCA,AE=CE=
AC=
.
连接PQ、PE,QE,则∠APE=∠QPE,∠PQE=∠CQE.
在四边形APQC中,∠DAC+∠APQ+∠PQC+∠DCA=360°(四边形内角和等于360°),
即2∠DAC+2∠APE+2∠CQE=360°,
∴∠DAC+∠APE+∠CQE=180°.
又∵∠DAC+∠APE+∠AEP=180°(三角形内角和定理),
∴∠AEP=∠CQE.
在△APE与△CEQ中,∵∠DAC=∠DCA,∠AEP=∠CQE,
∴△APE∽△CEQ,
∴
,即:
,
整理得:2t2﹣
t+3=0,
解得:t=
或t=
(t<
,所以舍去)
∴存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,此时t=
(适用于第29章和第30章)
(时间:90分钟
分值:100分)
一、选择题(每小题4分,共40分)
1.将y=x2向上平移2个单位后所得到的抛物线的解析式为(??
)
A.?y=x2﹣2?
B.?y=x2+2??
C.?y=(x﹣2)2?
D.?y=(x+2)2
2.如图29-Z-1所示,PA是⊙O的切线,切点为A,PA=2
,∠APO=30°,则⊙O的半径长为( )
A.4
B.2
C.2
D.3
图29-Z-1
图29-Z-2
3.如图29-Z-2,两个同心圆的半径分别为4
cm和5
cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
A.3
cm
B.4
cm
C.6
cm
D.8
cm
4.如图29-Z-3,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若
∠BCD=50°,则∠AOC的度数为( )
图29-Z-3
A.40°
B.50°
C.80°
D.100°
5.二次函数y=ax2+bx+c与一次函数y=ax+c,它们在同一直角坐标系中的图象大致是(?
)
A.????B.???
C.?????D.?
6.如图29-Z-4,圆的内接正五边形ABCDE的边长为a,圆的半径为r.下列等式成立的是( )
图29-Z-4
A.a=2rsin36°
B.a=2rcos36°
C.a=rsin36°
D.a=2rsin72°
7.如图,已知二次函数
y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:
①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;
其中正确的结论有(??
)
A.?1
个??B.?2
个??C.?3
个?D.?4
个
8.如图29-Z-5,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.连接BD,BE,CE,若∠CBD=33°,则∠BEC等于( )
A.66°
B.114°
C.123°
D.132°
图29-Z-5
图29-Z-6
9.如图29-Z-6所示,在等腰直角三角形ABC中,AB=AC=4,O为BC的中点,以点O为圆心作圆交BC于点M,N,与AB,AC相切,切点分别为D,E,则⊙O的半径和∠MND的度数分别为( )
A.2,22.5°
B.3,30°
C.3,22.5°
D.2,30°
10.如图29-Z-7,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至点C,过点C作直线OA的垂线,记为l,则下列说法正确的是( )
图29-Z-7
A.当BC等于0.5时,l与⊙O相离
B.当BC等于2时,l与⊙O相切
C.当BC等于1时,l与⊙O相交
D.当BC不为1时,l与⊙O不相切
二、填空题(每小题4分,共24分)
11.抛物线y=(x﹣2)2+1的顶点坐标是________.
12.二次函数y=x2+4x﹣3中,当x=﹣1时,y的值是________.
图29-Z-8
13.如图29-Z-8,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为________.
图29-Z-9
14.如图29-Z-9,PA与⊙O相切于点A,弦AB⊥OP,垂足为C,OP与⊙O相交于点D,已知OA=2,OP=4,则弦AB的长为________.
15.某工厂计划为一批长方体形状的产品涂上油漆,长方体的长和宽相等,高比长多0.5m,若长方体的长和宽用x(m)表示,长方体需涂油漆的表面积S(m2)表示为________.
16.如图29-Z-10,⊙M与x轴相切于原点,平行于y轴的直线交⊙M于P,Q两点,点P在点Q的下方.若点P的坐标是(2,1),则圆心M的坐标是________.
图29-Z-10
三、解答题(共36分)
17.(10分)如图29-Z-11,△ABC内接于⊙O,AB是⊙O的直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.
(1)判断AF与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为4,AF=3,求AC的长.
图29-Z-11
18.如图,抛物线y=
x2﹣x+a与x轴交于点A,B,与y轴交于点C,其顶点在直线y=﹣2x上.
(1)求a的值;
(2)求A,B的坐标;
(3)以AC,CB为一组邻边作?ACBD,则点D关于x轴的对称点D′是否在该抛物线上?请说明理由.
19.如图①,若二次函数y=
x2+bx+c的图象与x轴交于A(﹣2,0),B(3,0)两点,点A关于正比例函数y=
x的图象的对称点为C.
(1)求b、c的值;
(2)证明:点C在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数y=
x的图象于点D,连结AC,交正比例函数y=
x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.
参考答案:
1.B
2.C [解析]
连接OA.因为PA是⊙O的切线,所以OA⊥PA,OA=AP·tan30°=2.
故选C.
3.C
4.C [解析]
∵在⊙O中,AB为直径,BC为弦,CD为切线,∴∠OCD=90°.
∵∠BCD=50°,∴∠OCB=40°,∴∠AOC=80°.
5. A
6.A [解析]
如图,作OF⊥BC于点F.∵∠COF=72°÷2=36°,∴CF=r·sin36°,∴a=2rsin36°.
7.C
8.C [解析]
在⊙O中,∵∠CBD=33°,∴∠CAD=33°.∵点E是△ABC的内心,∴∠BAC=66°,∴∠EBC+∠ECB=(180°-66°)=57°,
∴∠BEC=180°-57°=123°.故选C.
9.A [解析]
∵AB为⊙O的切线,
∴OD⊥AB,∴∠ODB=∠A=90°.
又∠B=∠B,∴△OBD∽△CBA,
∴==,
∴OD=CA=2,∠MND=∠DOB=∠C=22.5°.
故选A.
10.D [解析]
设直线l与OA的垂足为D.
A项,∵BC=0.5,
∴OC=OB+CB=1.5.
∵∠AOB=60°,
∴∠ACO=30°,∴DO=OC=0.75<1,
∴l与⊙O相交,故A项错误.
B项,∵BC=2,
∴OC=OB+CB=3.
∵∠AOB=60°,
∴∠ACO=30°,∴DO=OC=1.5>1,
∴l与⊙O相离,故B项错误.
C项,∵BC=1,∴OC=OB+CB=2.
∵∠AOB=60°,
∴∠ACO=30°,∴DO=OC=1,
∴l与⊙O相切,故C项错误.
D项,∵BC≠1,
∴OC=OB+CB≠2.
∵∠AOB=60°,
∴∠ACO=30°,
∴DO=OC≠1,
∴l与⊙O不相切,故D项正确.故选D.
11.
(2,1)
12.
﹣6
13. [解析]
如图,连接OE,OF,ON,OG.
∵四边形ABCD为矩形,
∴∠A=∠B=90°.
又∵AD,AB,BC分别与⊙O相切于E,F,G三点,
又∵OE=OF=OG,
∴∠AEO=∠AFO=∠OFB=∠BGO=90°.
∴四边形AFOE,FBGO是正方形,
∴AF=BF=AE=BG=2,∴DE=3.
∵DM是⊙O的切线,
∴DN=DE=3,MN=MG,
∴CM=5-2-MN=3-MN.
在Rt△DMC中,DM2=CD2+CM2,
∴(3+MN)2=42+(3-MN)2,
解得MN=,
∴DM=DN+MN=3+=.故答案为.
14.2
[解析]
∵PA与⊙O相切于点A,
∴OA⊥AP,
∴△POA是直角三角形.
∵OA=2,OP=4,即OP=2OA,
∴∠P=30°,∠O=60°.
则在Rt△AOC中,OC=OA=1,
从而AC=,∴AB=2
.故答案为2
.
15.S=6x2+2x
16.(0,2.5) [解析]
连接MP,过点P作PA⊥y轴于点A,设点M的坐标是(0,b),且b>0,
∵PA⊥y轴,∴∠PAM=90°,∴AP2+AM2=MP2,∴22+(b-1)2=b2,解得b=2.5,故答案是(0,2.5).
17.解:(1)AF与⊙O相切.
理由:如图,连接
OC.
∵PC为⊙O的切线,∴∠OCP=90°.
∵AB是⊙O的直径,∴∠BCA=90°.
∵OF∥BC,∴∠AEO=∠BCA=90°,
∴OF⊥AC.
∵OC=OA,∴∠COF=∠AOF,
又CO=AO,OF=OF,∴△OCF≌△OAF,
∴∠OAF=∠OCF=90°,
∴FA⊥OA.
∵点A在⊙O上,∴AF与⊙O相切.
(2)∵⊙O的半径为4,AF=3,FA⊥OA,∴在Rt△OFA中,OF==
=5.
∵FA⊥OA,OF⊥AC,易证△AOE∽△FOA,
∴=
,即=
,
解得AE=,∴AC=2AE=.
18.
(1)解:∵抛物线y=
x2﹣x+a其顶点在直线y=﹣2x上.
∴抛物线y=
x2﹣x+a,
=
(x2﹣2x)+a,
=
(x﹣1)2﹣
+a,
∴顶点坐标为:(1,﹣
+a),
∴y=﹣2x,﹣
+a=﹣2×1,
∴a=﹣
(2)解:二次函数解析式为:y=
x2﹣x﹣
,
∵抛物线y=
x2﹣x﹣
与x轴交于点A,B,
∴0=
x2﹣x﹣
,
整理得:x2﹣2x﹣3=0,
解得:x=﹣1或3,
A(﹣1,0),B(3,0)
(3)解:作出平行四边形ACBD,作DE⊥AB,
在△AOC和△BDE中
∵
∴△AOC≌△BED(AAS),
∵AO=1,
∴BE=1,
∵二次函数解析式为:y=
x2﹣x﹣
,
∴图象与y轴交点坐标为:(0,﹣
),
∴CO=
,∴DE=
,
D点的坐标为:(2,
),
∴点D关于x轴的对称点D′坐标为:(2,﹣
),
代入解析式y=
x2﹣x﹣
,
∵左边=﹣
,右边=
×4﹣2﹣
=﹣
,
∴D′点在函数图象上.
19.
(1)解:∵点A(﹣2,0),B(3,0)在抛物线y=
x2+bx+c上,
∴
,
解得:b=﹣
,c=﹣
(2)解:设点F在直线y=
x上,且F(2,
).
如答图1所示,过点F作FH⊥x轴于点H,则FH=
,OH=2,
∴tan∠FOB=
=
,∴∠FOB=60°.
∴∠AOE=∠FOB=60°.
连接OC,过点C作CK⊥x轴于点K.
∵点A、C关于y=
x对称,∴OC=OA=2,∠COE=∠AOE=60°.
∴∠COK=180°﹣∠AOE﹣∠COE=60°.
在Rt△COK中,CK=OC?sin60°=2×
=
,OK=OC?cos60°=2×
=1.
∴C(1,﹣
).
抛物线的解析式为:y=
x2﹣
x﹣
,当x=1时,y=﹣
,
∴点C在所求二次函数的图象上
(3)解:假设存在.
如答图1所示,在Rt△ACK中,由勾股定理得:AC=
=
=
.
如答图2所示,∵OB=3,∴BD=3
,AB=OA+OB=5.
在Rt△ABD中,由勾股定理得:AD=
=
=2
.
∵点A、C关于y=
x对称,
∴CD=AD=2
,∠DAC=∠DCA,AE=CE=
AC=
.
连接PQ、PE,QE,则∠APE=∠QPE,∠PQE=∠CQE.
在四边形APQC中,∠DAC+∠APQ+∠PQC+∠DCA=360°(四边形内角和等于360°),
即2∠DAC+2∠APE+2∠CQE=360°,
∴∠DAC+∠APE+∠CQE=180°.
又∵∠DAC+∠APE+∠AEP=180°(三角形内角和定理),
∴∠AEP=∠CQE.
在△APE与△CEQ中,∵∠DAC=∠DCA,∠AEP=∠CQE,
∴△APE∽△CEQ,
∴
,即:
,
整理得:2t2﹣
t+3=0,
解得:t=
或t=
(t<
,所以舍去)
∴存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,此时t=
同课章节目录
