辽宁省营口市2020-2021学年高一上学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 辽宁省营口市2020-2021学年高一上学期期末考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 278.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-21 20:14:49 | ||
图片预览



文档简介
营口市普通高中2020—2021学年度上学期期末教学质量检测
高一年级数学试卷(试题卷)
试卷说明:试卷分为第I卷(选择题)和第II卷(非选择题)两部分,考试时间
120分钟,试卷满分150分。
第I卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.设全集U={1,2,3,4,5,6},集合A={1,3},B={3,4,6}则(CUA)IB=( )
(A) (B){2,5} (C){2,4} (D){4,6}
2.“xR,exx10”的否定是()
(A)xR,exx10 (B)xR,exx10
(C)xR,exx10 (D)xR,exx10
3.函数f(x)=false,则flog23( )
(A)3 (B)6 (C)12 (D)24
4.已知D为ABC所在平面内一点,3=,,则 ( )
(A) (B) (C) (D)
5.已知设alog30.2,b30.2,c0.23,则a,b,c的大小关系是( )
(A)abc (B)acb (C)bac (D)bca
6.在新冠肺炎疫情初始阶段,可以用指数模型::I(t) = ert (其中r为指数增长率)描述累计感染病例数I(t)随时间t(单位:天)的变化规律.有学者基于已有数据估计出累计感染病例数增加1倍需要的时间约为2天,据此,在新冠肺炎疫情初始阶段,指数增长率r的值约为( )(参考数值:ln20.69)
(A)0.345 (B)0.23 (C)0.69 (D)0.831
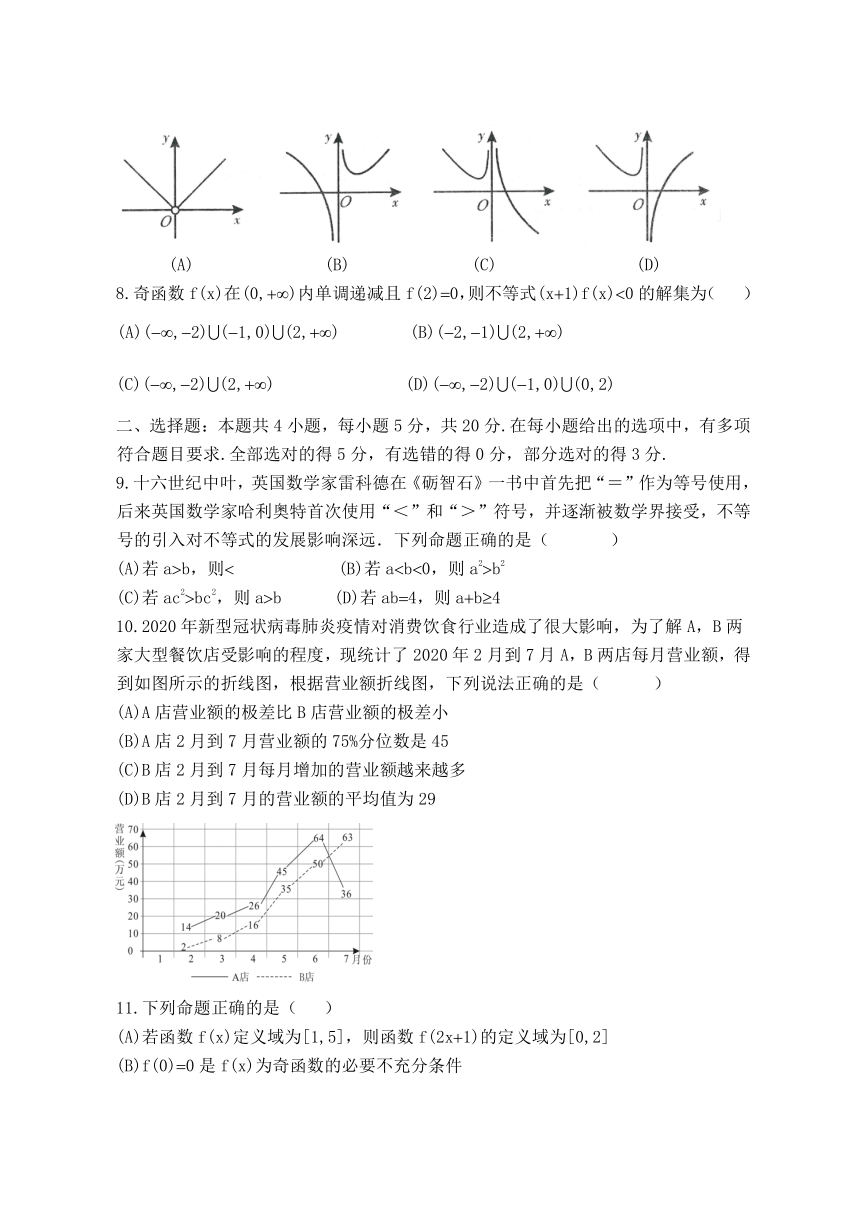
7.函数f(x)|x| (aR)的图像不可能是( )
(A) (B) (C) (D)
8.奇函数f(x)在(0,)内单调递减且f(2)0,则不等式(x1)f(x)0的解集为( )(A)(,2)(1,0)(2,) (B)(2,1)(2,)
(C)(,2)(2,) (D)(,2)(1,0)(0,2)
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.
9.十六世纪中叶,英国数学家雷科德在《砺智石》一书中首先把“=”作为等号使用,后来英国数学家哈利奥特首次使用“<”和“>”符号,并逐渐被数学界接受,不等号的引入对不等式的发展影响深远.下列命题正确的是( )
(A)若ab,则 (B)若ab0,则a2b2
(C)若ac2bc2,则ab (D)若ab4,则ab4
10.2020年新型冠状病毒肺炎疫情对消费饮食行业造成了很大影响,为了解A,B两家大型餐饮店受影响的程度,现统计了2020年2月到7月A,B两店每月营业额,得到如图所示的折线图,根据营业额折线图,下列说法正确的是( )
(A)A店营业额的极差比B店营业额的极差小
(B)A店2月到7月营业额的75%分位数是45
(C)B店2月到7月每月增加的营业额越来越多
(D)B店2月到7月的营业额的平均值为29
11.下列命题正确的是( )
(A)若函数f(x)定义域为[1,5],则函数f(2x1)的定义域为[0,2]
(B)f(0)0是f(x)为奇函数的必要不充分条件
(C)正实数x,y满足3x4y5xy0,则x3y的最小值为5
(D)函数f x= 在区间3m2,m2内单调递增,则实数m的取值范围为 [,2]
12.已知函数fxln,gx=2xm12xm1,h(x)f(x)g(x),则下列说法正确的是( )
(A)当m4时,fx的值域为R
(B)mR,使得函数gx为偶函数
(C)若函数fx有零点,则实数m的取值范围是(,5]
(D)当m3时,不等式hx3h(2x1)的解集为(,2)(2,)
第II卷
三、填空题:本题共4小题,每小题5分,共20分.
13.幂函数f(x)的图像经过点(4,2),则f(x) .
14.为了实现绿色发展,避免用电浪费,某城市对居民生活用电实行“阶梯电价”.计费方法如表所示,若某户居民某月交纳电费227元,则该月用电量为 度.
每户每月用电量
电价
不超过210度的部分
0.5元/度
超过210度但不超过400度的部分
0.6元/度
超过400度的部分
0.8元/度
15.已知一组样本数据x1,x2,…,x10,且++…+=2020, 平均数 11,则该组数据的标准差为 .
16.已知函数f (x) =ex-a + x2 ,g(x) = 2x-4ea-x ,x0R ,使得 f (x0 ) - g(x0 ) =3 ,则a= .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)甲、乙二人独立破译同一密码,甲破译密码的概率为0.7,乙破译密码的概率为0.6.记事件A:甲破译密码,事件B:乙破译密码.
(Ⅰ)求甲、乙二人都破译密码的概率;
(Ⅱ)求恰有一人破译密码的概率.
18.(本小题满分12分)已知向量 (3,2), (1,2), (4,1)
(Ⅰ)若 m n,求m,n的值;
(Ⅱ)若向量满足()//( ),| |2,求的坐标.
19.(本小题满分12分)已知二次函数fxax2bxc,若不等式fx20的解集为1,2,且方程fxx0有两个相等的实数根.
(Ⅰ)求fx的解析式;
(Ⅱ)若x1,,fxmx0成立,求实数m的取值范围.
20.(本小题满分12分)2021年起,辽宁省将实行“3+1+2”高考模式,为让学生适应新高考的赋分模式某校在一次校考中使用赋分制给高三年级学生的化学成绩进行赋分,具体赋分方案如下:先按照考生原始分从高到低按比例划定A、B、C、D、E共五个等级,然后在相应赋分区间内利用转换公式进行赋分。
A等级排名占比15%,赋分分数区间是86-100;
B等级排名占比35%,赋分分数区间是71-85;
C等级排名占比35%,赋分分数区间是56-70;
D等级排名占比13%,赋分分数区间是41-55;
E等级排名占比2%,赋分分数区间是30-40;
现从全年级的化学成绩中随机抽取100名学生的原始成绩(未赋分)进行分析,其频率分布直方图如图所示:
(Ⅰ)求图中a的值;
(Ⅱ)用样本估计总体的方法,估计该校本次化学成绩原始分不少于多少分才能达到赋分后的C等级及以上(含C等级)?(结果保留整数)
(Ⅲ)若采用分层抽样的方法,从原始成绩在[40,50)和[50,60)内的学生中共抽取5人,查看他们的答题情况来分析知识点上的缺漏,再从中选取2人进行调查分析,求这2人中恰有一人原始成绩在[40,50)内的概率.
21.(本小题满分12分)
已知 ,且函数gx.
(Ⅰ)判断gx的奇偶性,并证明你的结论;
(Ⅱ)设hxx2c,对任意的x1R,总存在x2[2,2],使得g(x1)h(x2)成立,求实数c的取值范围.
在以下①,②两个条件中,选择一个条件,将上面的题目补充完整,先求出a,b的值,并解答本题.
①函数fxx2(2a)x4在定义域b1,b1上为偶函数;
②函数fxaxb a1在1,2上的值域为2,4;
注:如果选择多个条件分别解答,按第一个解答计分.
22.(本小题满分12分)已知函数fx=aR.
(Ⅰ)当a1时,利用单调性定义证明fx在R上是增函数;
(Ⅱ)若存在x10x2,使fx1fx21,求实数a的取值范围.
营口市普通高中 2020—2021 学年度上学期
期末教学质量检测一年级数学参考答案
一、选择题
1-8.DBBA DACA
二、选择题
9.BC 10.ABD 11.AC 12.BCD
三、填空题
13. 14.410 15.9 16.1ln2
四、解答题
17.解:
(1)事件“甲、乙二人都破译密码”可表示为AB,事件A,B相互独立
由题意可知P(A)0.7,P(B)0.6,
所以P(AB)P(A)P(B)0.70.60.42
(2)事件“恰有一人破译密码”可表示为B+A,且B,A互斥
所以P(B+A)P(B)+P(A)P()P(B)+P(A)P()0.30.60.70.40.46
18.解:(1)若 m n,则(4,1)m(3,2)n(1,2)
即 所以
(2)设(x,y),则(x4,y1),(2,4)
(-)//(), |-|2
解得或
所以(2,3)或(6,5)
19.解:因为fx2ax2bxc20的解集为1,2,
所以1,2是方程ax2bxc20的两根,
由韦达定理得
且a0
解得b3a,c2a2
所以ax2(b1)xc0,即ax2(13a)x2a20
又因为方程fxx0有两个相等的实数根
所以(13a) 24a(2a2)0
解得a1,所以b3,c4
所以f(x)x23x4
(2)解法1:由(1)可得f(x)mxx2(3m)x40,x1,,
所以(3m)xx24,则mx3,x1,
又x3-3=1,当且仅当x,即x=2时等号成立
所以x1,,使fxmx0成立,等价为m (x3) min成立,
所以m1.综上所述m的取值范围是(1,)
20.解:(1)由题意(0.0100.0150.015a0.0250.005)101,所以a0.030;
(2)由已知等级达到C及以上所占排名等级占比为15%+35%+35%=85%
假设原始分不少于x分可以达到赋分后的C等级及以上
则有(0.0050.0250.0300.015)10(60x)0.0150.85
解得x≈53.33(分),所以原始分不少于54分才能达到赋分后的C等级及以上
(如果答案取53扣1分)
(3)由题知得分在[40,50)和[50,60)内的频率分别为0.1和0.15,
则抽取的5人中,得分在[40,50)内的有2人,得分在[50,60)的有3人
记得分在[50,60)内的3位学生为a,b,c,得分在[40,50)内的2位学生为D,E,则从5人中任选2人,样本空间可记为{ab,ac,aD,aE,bc,bD,bE,cD,cE,DE}共包含10个样本
用A表示“这2人中恰有一人得分在[40,50)内”,则A{aD,aE,bD,bE,cD,cE}A包含6个样本,
所以63105P(A).
20.解:①由f x x2(2a)x4,在b1,b1上是偶函数,
则0,且b1b10,所以a2,b0;
②当a1时,f xaxb在1,2上单调递增,则有,得a2a20,
得a2,b0;
由①或②得gx
(1)gx为奇函数(没证明,判断正确得1分)
证明:gx的定义域为R............................3分
因为g-x= -gx,则gx为奇函数.............................5分
(2)当x0时,gx,因为4,当且仅当即x1时等号成立,
所以0gx
当x0时,因为gx为奇函数,所以 gx0
当x0时,g00;
所以gx的值域为 [, ]
22.(1) ,任取x1, x2R ,且x1x2
因为x1x2,所以又因为 a 1
所以 f x1 f x2 0 ,即 f x1 f x2
所以 a 1时, f x 在 R 上是增函数..........................4 分
(2)①当 a 1 0时,即 a 1, f x 恒大于等于 1, f x1 f x2 2 ,故不成立
②当 a 1 0时,即 a 1 , f x 在R上为增函数,
若 x 0 时, 1 f (x ) f (0) ,所以 f (x) 的值域为 ( ,1)
若 x 0 时, f (x) 值域为(a , ) a ,则 y 1 f (x) 值域( ,1+a )
若存在x1 0 x2 ,使 f x2 1 f x1 ,等价于( ,1) ( ,1+a )
所以 ,解得 a 1
综上所述,实数 a 的取值范围是 ( ,1)
高一年级数学试卷(试题卷)
试卷说明:试卷分为第I卷(选择题)和第II卷(非选择题)两部分,考试时间
120分钟,试卷满分150分。
第I卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.设全集U={1,2,3,4,5,6},集合A={1,3},B={3,4,6}则(CUA)IB=( )
(A) (B){2,5} (C){2,4} (D){4,6}
2.“xR,exx10”的否定是()
(A)xR,exx10 (B)xR,exx10
(C)xR,exx10 (D)xR,exx10
3.函数f(x)=false,则flog23( )
(A)3 (B)6 (C)12 (D)24
4.已知D为ABC所在平面内一点,3=,,则 ( )
(A) (B) (C) (D)
5.已知设alog30.2,b30.2,c0.23,则a,b,c的大小关系是( )
(A)abc (B)acb (C)bac (D)bca
6.在新冠肺炎疫情初始阶段,可以用指数模型::I(t) = ert (其中r为指数增长率)描述累计感染病例数I(t)随时间t(单位:天)的变化规律.有学者基于已有数据估计出累计感染病例数增加1倍需要的时间约为2天,据此,在新冠肺炎疫情初始阶段,指数增长率r的值约为( )(参考数值:ln20.69)
(A)0.345 (B)0.23 (C)0.69 (D)0.831
7.函数f(x)|x| (aR)的图像不可能是( )
(A) (B) (C) (D)
8.奇函数f(x)在(0,)内单调递减且f(2)0,则不等式(x1)f(x)0的解集为( )(A)(,2)(1,0)(2,) (B)(2,1)(2,)
(C)(,2)(2,) (D)(,2)(1,0)(0,2)
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.
9.十六世纪中叶,英国数学家雷科德在《砺智石》一书中首先把“=”作为等号使用,后来英国数学家哈利奥特首次使用“<”和“>”符号,并逐渐被数学界接受,不等号的引入对不等式的发展影响深远.下列命题正确的是( )
(A)若ab,则 (B)若ab0,则a2b2
(C)若ac2bc2,则ab (D)若ab4,则ab4
10.2020年新型冠状病毒肺炎疫情对消费饮食行业造成了很大影响,为了解A,B两家大型餐饮店受影响的程度,现统计了2020年2月到7月A,B两店每月营业额,得到如图所示的折线图,根据营业额折线图,下列说法正确的是( )
(A)A店营业额的极差比B店营业额的极差小
(B)A店2月到7月营业额的75%分位数是45
(C)B店2月到7月每月增加的营业额越来越多
(D)B店2月到7月的营业额的平均值为29
11.下列命题正确的是( )
(A)若函数f(x)定义域为[1,5],则函数f(2x1)的定义域为[0,2]
(B)f(0)0是f(x)为奇函数的必要不充分条件
(C)正实数x,y满足3x4y5xy0,则x3y的最小值为5
(D)函数f x= 在区间3m2,m2内单调递增,则实数m的取值范围为 [,2]
12.已知函数fxln,gx=2xm12xm1,h(x)f(x)g(x),则下列说法正确的是( )
(A)当m4时,fx的值域为R
(B)mR,使得函数gx为偶函数
(C)若函数fx有零点,则实数m的取值范围是(,5]
(D)当m3时,不等式hx3h(2x1)的解集为(,2)(2,)
第II卷
三、填空题:本题共4小题,每小题5分,共20分.
13.幂函数f(x)的图像经过点(4,2),则f(x) .
14.为了实现绿色发展,避免用电浪费,某城市对居民生活用电实行“阶梯电价”.计费方法如表所示,若某户居民某月交纳电费227元,则该月用电量为 度.
每户每月用电量
电价
不超过210度的部分
0.5元/度
超过210度但不超过400度的部分
0.6元/度
超过400度的部分
0.8元/度
15.已知一组样本数据x1,x2,…,x10,且++…+=2020, 平均数 11,则该组数据的标准差为 .
16.已知函数f (x) =ex-a + x2 ,g(x) = 2x-4ea-x ,x0R ,使得 f (x0 ) - g(x0 ) =3 ,则a= .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)甲、乙二人独立破译同一密码,甲破译密码的概率为0.7,乙破译密码的概率为0.6.记事件A:甲破译密码,事件B:乙破译密码.
(Ⅰ)求甲、乙二人都破译密码的概率;
(Ⅱ)求恰有一人破译密码的概率.
18.(本小题满分12分)已知向量 (3,2), (1,2), (4,1)
(Ⅰ)若 m n,求m,n的值;
(Ⅱ)若向量满足()//( ),| |2,求的坐标.
19.(本小题满分12分)已知二次函数fxax2bxc,若不等式fx20的解集为1,2,且方程fxx0有两个相等的实数根.
(Ⅰ)求fx的解析式;
(Ⅱ)若x1,,fxmx0成立,求实数m的取值范围.
20.(本小题满分12分)2021年起,辽宁省将实行“3+1+2”高考模式,为让学生适应新高考的赋分模式某校在一次校考中使用赋分制给高三年级学生的化学成绩进行赋分,具体赋分方案如下:先按照考生原始分从高到低按比例划定A、B、C、D、E共五个等级,然后在相应赋分区间内利用转换公式进行赋分。
A等级排名占比15%,赋分分数区间是86-100;
B等级排名占比35%,赋分分数区间是71-85;
C等级排名占比35%,赋分分数区间是56-70;
D等级排名占比13%,赋分分数区间是41-55;
E等级排名占比2%,赋分分数区间是30-40;
现从全年级的化学成绩中随机抽取100名学生的原始成绩(未赋分)进行分析,其频率分布直方图如图所示:
(Ⅰ)求图中a的值;
(Ⅱ)用样本估计总体的方法,估计该校本次化学成绩原始分不少于多少分才能达到赋分后的C等级及以上(含C等级)?(结果保留整数)
(Ⅲ)若采用分层抽样的方法,从原始成绩在[40,50)和[50,60)内的学生中共抽取5人,查看他们的答题情况来分析知识点上的缺漏,再从中选取2人进行调查分析,求这2人中恰有一人原始成绩在[40,50)内的概率.
21.(本小题满分12分)
已知 ,且函数gx.
(Ⅰ)判断gx的奇偶性,并证明你的结论;
(Ⅱ)设hxx2c,对任意的x1R,总存在x2[2,2],使得g(x1)h(x2)成立,求实数c的取值范围.
在以下①,②两个条件中,选择一个条件,将上面的题目补充完整,先求出a,b的值,并解答本题.
①函数fxx2(2a)x4在定义域b1,b1上为偶函数;
②函数fxaxb a1在1,2上的值域为2,4;
注:如果选择多个条件分别解答,按第一个解答计分.
22.(本小题满分12分)已知函数fx=aR.
(Ⅰ)当a1时,利用单调性定义证明fx在R上是增函数;
(Ⅱ)若存在x10x2,使fx1fx21,求实数a的取值范围.
营口市普通高中 2020—2021 学年度上学期
期末教学质量检测一年级数学参考答案
一、选择题
1-8.DBBA DACA
二、选择题
9.BC 10.ABD 11.AC 12.BCD
三、填空题
13. 14.410 15.9 16.1ln2
四、解答题
17.解:
(1)事件“甲、乙二人都破译密码”可表示为AB,事件A,B相互独立
由题意可知P(A)0.7,P(B)0.6,
所以P(AB)P(A)P(B)0.70.60.42
(2)事件“恰有一人破译密码”可表示为B+A,且B,A互斥
所以P(B+A)P(B)+P(A)P()P(B)+P(A)P()0.30.60.70.40.46
18.解:(1)若 m n,则(4,1)m(3,2)n(1,2)
即 所以
(2)设(x,y),则(x4,y1),(2,4)
(-)//(), |-|2
解得或
所以(2,3)或(6,5)
19.解:因为fx2ax2bxc20的解集为1,2,
所以1,2是方程ax2bxc20的两根,
由韦达定理得
且a0
解得b3a,c2a2
所以ax2(b1)xc0,即ax2(13a)x2a20
又因为方程fxx0有两个相等的实数根
所以(13a) 24a(2a2)0
解得a1,所以b3,c4
所以f(x)x23x4
(2)解法1:由(1)可得f(x)mxx2(3m)x40,x1,,
所以(3m)xx24,则mx3,x1,
又x3-3=1,当且仅当x,即x=2时等号成立
所以x1,,使fxmx0成立,等价为m (x3) min成立,
所以m1.综上所述m的取值范围是(1,)
20.解:(1)由题意(0.0100.0150.015a0.0250.005)101,所以a0.030;
(2)由已知等级达到C及以上所占排名等级占比为15%+35%+35%=85%
假设原始分不少于x分可以达到赋分后的C等级及以上
则有(0.0050.0250.0300.015)10(60x)0.0150.85
解得x≈53.33(分),所以原始分不少于54分才能达到赋分后的C等级及以上
(如果答案取53扣1分)
(3)由题知得分在[40,50)和[50,60)内的频率分别为0.1和0.15,
则抽取的5人中,得分在[40,50)内的有2人,得分在[50,60)的有3人
记得分在[50,60)内的3位学生为a,b,c,得分在[40,50)内的2位学生为D,E,则从5人中任选2人,样本空间可记为{ab,ac,aD,aE,bc,bD,bE,cD,cE,DE}共包含10个样本
用A表示“这2人中恰有一人得分在[40,50)内”,则A{aD,aE,bD,bE,cD,cE}A包含6个样本,
所以63105P(A).
20.解:①由f x x2(2a)x4,在b1,b1上是偶函数,
则0,且b1b10,所以a2,b0;
②当a1时,f xaxb在1,2上单调递增,则有,得a2a20,
得a2,b0;
由①或②得gx
(1)gx为奇函数(没证明,判断正确得1分)
证明:gx的定义域为R............................3分
因为g-x= -gx,则gx为奇函数.............................5分
(2)当x0时,gx,因为4,当且仅当即x1时等号成立,
所以0gx
当x0时,因为gx为奇函数,所以 gx0
当x0时,g00;
所以gx的值域为 [, ]
22.(1) ,任取x1, x2R ,且x1x2
因为x1x2,所以又因为 a 1
所以 f x1 f x2 0 ,即 f x1 f x2
所以 a 1时, f x 在 R 上是增函数..........................4 分
(2)①当 a 1 0时,即 a 1, f x 恒大于等于 1, f x1 f x2 2 ,故不成立
②当 a 1 0时,即 a 1 , f x 在R上为增函数,
若 x 0 时, 1 f (x ) f (0) ,所以 f (x) 的值域为 ( ,1)
若 x 0 时, f (x) 值域为(a , ) a ,则 y 1 f (x) 值域( ,1+a )
若存在x1 0 x2 ,使 f x2 1 f x1 ,等价于( ,1) ( ,1+a )
所以 ,解得 a 1
综上所述,实数 a 的取值范围是 ( ,1)
同课章节目录
