人教版八年级数学下册:17.1.1 勾股定理 课件(26张ppt)
文档属性
| 名称 | 人教版八年级数学下册:17.1.1 勾股定理 课件(26张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 760.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-21 22:34:57 | ||
图片预览






文档简介
八年级下册
勾股定理
学习目标
1、了解勾股定理的发现过程;
2、掌握勾股定理的内容,会用面积法证明勾股定理.
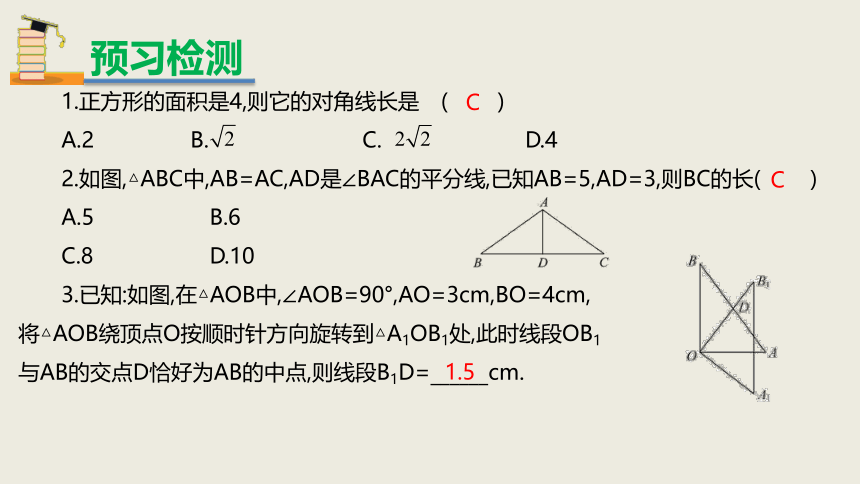
1.正方形的面积是4,则它的对角线长是 ( )
A.2 B. C. D.4
2.如图,△ABC中,AB=AC,AD是∠BAC的平分线,已知AB=5,AD=3,则BC的长( )
A.5 B.6
C.8 D.10
3.已知:如图,在△AOB中,∠AOB=90°,AO=3cm,BO=4cm,
将△AOB绕顶点O按顺时针方向旋转到△A1OB1处,此时线段OB1
与AB的交点D恰好为AB的中点,则线段B1D=______cm.
C
C
1.5
预习检测
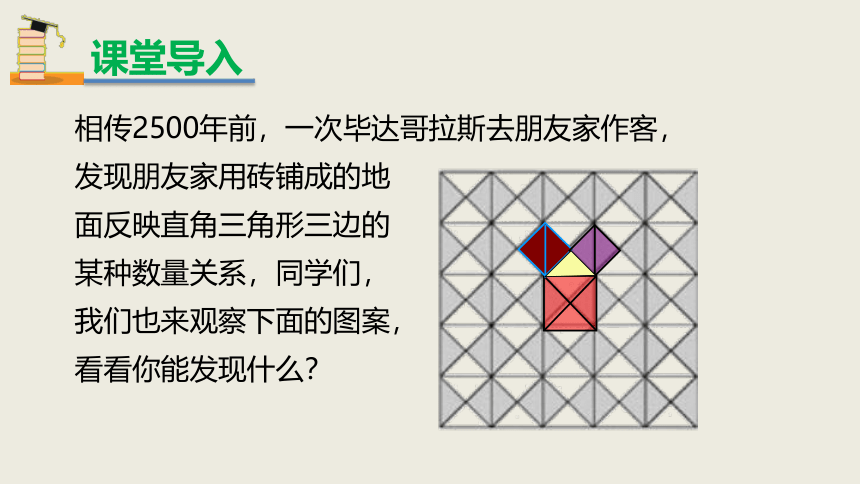
相传2500年前,一次毕达哥拉斯去朋友家作客,
发现朋友家用砖铺成的地
面反映直角三角形三边的
某种数量关系,同学们,
我们也来观察下面的图案,
看看你能发现什么?
课堂导入
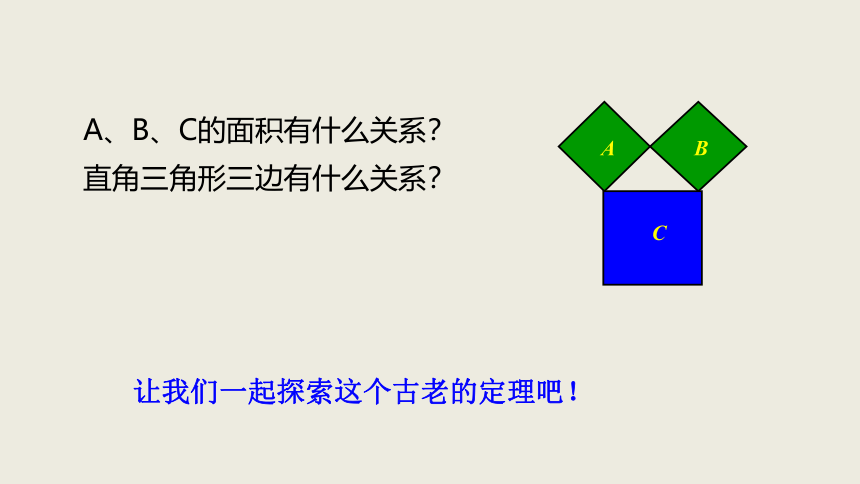
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
A
B
C
让我们一起探索这个古老的定理吧!
探究点一
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦. 图1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.
弦
勾
课堂探究
问题1:正方形A中含有____个小方格,即A的面积
是____个单位面积.
正方形B中含有____个小方格,即B的面积是___个单位面积.
正方形C中含有____个小方格,即C的面积是___个单位面积.
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?______________________________________________________________________.
(3)你能发现图1-1三个正方形A,B,C的面积之间有什么关系?图1-2中的呢?__________________________.
9
9
9
9
18
18
正方形A、B、C分别含有4个、4个、8个小方格;面积各是4、4、8
SA+SB=SC
问题2:(1)观察图1-3、图1-4,并填写下表(每个小方格的面积为1):
(2)三个正方形A,B,C的面积之间有什么关系?________________________
16
9
25
4
9
13
SA+SB=SC
这样就通过推理证实了命题1的正确性,经过证明被确认的命题叫做定理,命题1与直角三角形的边有关,我国把它称为勾股定理.
如果直角三角形两直角边长分别为a、b,斜边长为c,那么 。
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦. 在西方又称毕达哥拉斯定理.
a? + b? = c?
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
定义:直角三角形两直角边的平方和等于斜边的平方.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
数学表达式:
在Rt△ABC中,∠C=90°,AB=c,AC=b,BC= a ,则a2+b2=c2.
探究点二
问题1:由上面的几个例子,我们猜想:
命题1 如果直角三角形两直角边长分别为a、b,
斜边长为c,那么a?+b?=c?.
这个命题的证明方法:(1)如图
(2)赵爽利用弦图证明。
显然4个 的面积+ 的面积=该图案的面积.
即4×12× +( b-a ) ?=c?,化简后得到 .
?
直角三角形
中间小正方形
ab
a? + b? = c?
课堂探究
问题2:⑴.一个直角三角形,两直角边长分别是3和4,则斜边的长是 ;
⑵.已知在Rt△ABC中,∠B=90°,a.b.c是△ABC的三边,则(用字母表示)
①c= .(已知a.b,求c)
②a= .(已知b.c,求a)
③b= .(已知a.c,求b)
⑶ 如下图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积的和是______________cm?。
5
49
例1 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)已知a=b=6,求c;
(3)已知a∶b=2∶1,c=5,求b.
解:(1)∵∠C=90°,a=b=6,
∴由勾股定理,得????=????2+????2=62+62=62.
(2)∵∠C=90°,c=3,b=2,
∴由勾股定理,得????=????2?????2=32?22=5.
(3)∵∠C=90°,a∶b=2∶1,∴a=2b.
又c=5,由勾股定理,得(2b)2+b2=52,
解得b=5.
?
例题解析
利用勾股定理求直角三角形的边长的方法:一般都要经过“一分二代三化简”这“三步曲”,
即一分:分清哪条边是斜边,哪些是直角边;
二代:将已知边长及两边之间的关系式代入a2+b2=c2 (假设c是斜边);
三化简.
方法总结
1、 若一个直角三角形的两直角边的长分别为a,b,斜边长为c,则下列关于a,b,c的关系式中不正确的是( )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
2、在△ABC中,AB=10,AC=2 10?,BC边上的高AD=6,则另一边BC等于( )
A.10 B.8
C.6或10 D.8或10
?
C
C
试一试
3、如图,一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm.现将纸片折叠,使点A与点B重合,那么折痕长等于__________cm.
解:因为∠C=90°,AC=8cm,BC=6cm,
所以由勾股定理可得,AB=10cm.
又因为将纸片折叠:点A与点B重合,
所以∠ADE=90°,AD=5cm.
连接BE.设AE=x,
则CE=8-x,BE=x,
所以(8-x) ?+6?=x?,解得x= .
在Rt△BDE中,BE= cm,BD=5cm,
所以DE= (cm).
答案:
4、如图1,在Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,则EB′=________.
解:根据折叠可得BE=EB′,AB′=AB=3,
设BE=EB′=x,则EC=4-x,
∵∠B=90°,AB=3,BC=4,
∴在Rt△ABC中,由勾股定理得,AC= =5,
∴B′C=5-3=2,在Rt△B′EC中,由勾股定理得,x?+2?=(4-x) ?,解得x=1.5.
答案:1.5
5、设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
解:(1)????=????2?????2=102?62=8;
(2)????=????2+????2=52+122=13.
(3)????=????2?????2=252?152=20.
?
1.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,
若AC=6,BC=8,则CD等于( )
A.1 B.2 C.3 D.4.8
2.如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC
折叠,使点A与BC的中点D重合,折痕为MN,则线段BN的
长为________.
3.这个图案是我国汉代的赵爽在注解《周髀算经》时
给出的,人们称它为“赵爽弦图”.此图案的示意图如图2,
其中四边形ABCD和四边形EFGH都是正方形,△ABF,△BCG,
△CDH,△DAE是四个全等的直角三角形.若EF=2,DE=8,则AB的长为__________.
4
D
10
随堂检测
4.如图,在Rt△ABC中,∠ACB=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为 ( )
A.225 B.200
C.250 D.150
5.如图是一株美丽的勾股树,其中所有的四边形都是正方形,
所有的三角形都是直角三角形,若正方形A、B、C、D的面积分
别为2,5,1,2.则最大的正方形E的面积是__________.
A
10
6.四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2 EF,则正方形ABCD的面积为 ( )
A.12S B.10S
C.9S D.8S
C
7.在△ABC中,已知BD和CE分别是边AC,AB上的中线,且BD⊥CE,垂足为O,若OD=2cm,
OE=4cm, 则线段AO的长度为为多少cm?
解:如图,连接AO,作OF⊥AB于点F,
∵BD,CE是△ABC的中线,
∴OB=2OD=4,
∵OE=4,BD⊥CE,
∴△BOE是等腰直角三角形,
∴AE=BE=4 ,
∴OF=EF=2 ,AF=6 ,
∴AO=
线段AO的长度为为4 cm
1.内容:直角三角形两直角边的平方和等于斜边的平方;?
表示方法:如果直角三角形的两直角边分别为a,b,斜边为c,那么a?+b?=c?
2.勾股定理的证明?
勾股定理的证明方法很多,常见的是拼图的方法?
用拼图的方法验证勾股定理的思路是:?
图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变;
课堂小结
书面作业:完成相关书本作业
布置作业
再见
勾股定理
学习目标
1、了解勾股定理的发现过程;
2、掌握勾股定理的内容,会用面积法证明勾股定理.
1.正方形的面积是4,则它的对角线长是 ( )
A.2 B. C. D.4
2.如图,△ABC中,AB=AC,AD是∠BAC的平分线,已知AB=5,AD=3,则BC的长( )
A.5 B.6
C.8 D.10
3.已知:如图,在△AOB中,∠AOB=90°,AO=3cm,BO=4cm,
将△AOB绕顶点O按顺时针方向旋转到△A1OB1处,此时线段OB1
与AB的交点D恰好为AB的中点,则线段B1D=______cm.
C
C
1.5
预习检测
相传2500年前,一次毕达哥拉斯去朋友家作客,
发现朋友家用砖铺成的地
面反映直角三角形三边的
某种数量关系,同学们,
我们也来观察下面的图案,
看看你能发现什么?
课堂导入
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
A
B
C
让我们一起探索这个古老的定理吧!
探究点一
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦. 图1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.
弦
勾
课堂探究
问题1:正方形A中含有____个小方格,即A的面积
是____个单位面积.
正方形B中含有____个小方格,即B的面积是___个单位面积.
正方形C中含有____个小方格,即C的面积是___个单位面积.
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?______________________________________________________________________.
(3)你能发现图1-1三个正方形A,B,C的面积之间有什么关系?图1-2中的呢?__________________________.
9
9
9
9
18
18
正方形A、B、C分别含有4个、4个、8个小方格;面积各是4、4、8
SA+SB=SC
问题2:(1)观察图1-3、图1-4,并填写下表(每个小方格的面积为1):
(2)三个正方形A,B,C的面积之间有什么关系?________________________
16
9
25
4
9
13
SA+SB=SC
这样就通过推理证实了命题1的正确性,经过证明被确认的命题叫做定理,命题1与直角三角形的边有关,我国把它称为勾股定理.
如果直角三角形两直角边长分别为a、b,斜边长为c,那么 。
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦. 在西方又称毕达哥拉斯定理.
a? + b? = c?
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
定义:直角三角形两直角边的平方和等于斜边的平方.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
数学表达式:
在Rt△ABC中,∠C=90°,AB=c,AC=b,BC= a ,则a2+b2=c2.
探究点二
问题1:由上面的几个例子,我们猜想:
命题1 如果直角三角形两直角边长分别为a、b,
斜边长为c,那么a?+b?=c?.
这个命题的证明方法:(1)如图
(2)赵爽利用弦图证明。
显然4个 的面积+ 的面积=该图案的面积.
即4×12× +( b-a ) ?=c?,化简后得到 .
?
直角三角形
中间小正方形
ab
a? + b? = c?
课堂探究
问题2:⑴.一个直角三角形,两直角边长分别是3和4,则斜边的长是 ;
⑵.已知在Rt△ABC中,∠B=90°,a.b.c是△ABC的三边,则(用字母表示)
①c= .(已知a.b,求c)
②a= .(已知b.c,求a)
③b= .(已知a.c,求b)
⑶ 如下图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积的和是______________cm?。
5
49
例1 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)已知a=b=6,求c;
(3)已知a∶b=2∶1,c=5,求b.
解:(1)∵∠C=90°,a=b=6,
∴由勾股定理,得????=????2+????2=62+62=62.
(2)∵∠C=90°,c=3,b=2,
∴由勾股定理,得????=????2?????2=32?22=5.
(3)∵∠C=90°,a∶b=2∶1,∴a=2b.
又c=5,由勾股定理,得(2b)2+b2=52,
解得b=5.
?
例题解析
利用勾股定理求直角三角形的边长的方法:一般都要经过“一分二代三化简”这“三步曲”,
即一分:分清哪条边是斜边,哪些是直角边;
二代:将已知边长及两边之间的关系式代入a2+b2=c2 (假设c是斜边);
三化简.
方法总结
1、 若一个直角三角形的两直角边的长分别为a,b,斜边长为c,则下列关于a,b,c的关系式中不正确的是( )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
2、在△ABC中,AB=10,AC=2 10?,BC边上的高AD=6,则另一边BC等于( )
A.10 B.8
C.6或10 D.8或10
?
C
C
试一试
3、如图,一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm.现将纸片折叠,使点A与点B重合,那么折痕长等于__________cm.
解:因为∠C=90°,AC=8cm,BC=6cm,
所以由勾股定理可得,AB=10cm.
又因为将纸片折叠:点A与点B重合,
所以∠ADE=90°,AD=5cm.
连接BE.设AE=x,
则CE=8-x,BE=x,
所以(8-x) ?+6?=x?,解得x= .
在Rt△BDE中,BE= cm,BD=5cm,
所以DE= (cm).
答案:
4、如图1,在Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,则EB′=________.
解:根据折叠可得BE=EB′,AB′=AB=3,
设BE=EB′=x,则EC=4-x,
∵∠B=90°,AB=3,BC=4,
∴在Rt△ABC中,由勾股定理得,AC= =5,
∴B′C=5-3=2,在Rt△B′EC中,由勾股定理得,x?+2?=(4-x) ?,解得x=1.5.
答案:1.5
5、设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
解:(1)????=????2?????2=102?62=8;
(2)????=????2+????2=52+122=13.
(3)????=????2?????2=252?152=20.
?
1.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,
若AC=6,BC=8,则CD等于( )
A.1 B.2 C.3 D.4.8
2.如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC
折叠,使点A与BC的中点D重合,折痕为MN,则线段BN的
长为________.
3.这个图案是我国汉代的赵爽在注解《周髀算经》时
给出的,人们称它为“赵爽弦图”.此图案的示意图如图2,
其中四边形ABCD和四边形EFGH都是正方形,△ABF,△BCG,
△CDH,△DAE是四个全等的直角三角形.若EF=2,DE=8,则AB的长为__________.
4
D
10
随堂检测
4.如图,在Rt△ABC中,∠ACB=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为 ( )
A.225 B.200
C.250 D.150
5.如图是一株美丽的勾股树,其中所有的四边形都是正方形,
所有的三角形都是直角三角形,若正方形A、B、C、D的面积分
别为2,5,1,2.则最大的正方形E的面积是__________.
A
10
6.四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2 EF,则正方形ABCD的面积为 ( )
A.12S B.10S
C.9S D.8S
C
7.在△ABC中,已知BD和CE分别是边AC,AB上的中线,且BD⊥CE,垂足为O,若OD=2cm,
OE=4cm, 则线段AO的长度为为多少cm?
解:如图,连接AO,作OF⊥AB于点F,
∵BD,CE是△ABC的中线,
∴OB=2OD=4,
∵OE=4,BD⊥CE,
∴△BOE是等腰直角三角形,
∴AE=BE=4 ,
∴OF=EF=2 ,AF=6 ,
∴AO=
线段AO的长度为为4 cm
1.内容:直角三角形两直角边的平方和等于斜边的平方;?
表示方法:如果直角三角形的两直角边分别为a,b,斜边为c,那么a?+b?=c?
2.勾股定理的证明?
勾股定理的证明方法很多,常见的是拼图的方法?
用拼图的方法验证勾股定理的思路是:?
图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变;
课堂小结
书面作业:完成相关书本作业
布置作业
再见
