八年级下册17.1.1勾股定理课件(共25张ppt)
文档属性
| 名称 | 八年级下册17.1.1勾股定理课件(共25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 07:26:57 | ||
图片预览






文档简介
17.1.1 勾股定理
学习目标
1
2
掌握勾股定理
了解关于勾股定理的一些文化历史背景,会用面积法来证明勾股定理
3
会用勾股定理进行简单的计算
学习重难点
重点
难点
掌握勾股定理
会用勾股定理进行简单的计算
一、提出问题
边 角
等角对等边
等边对等角
直角三角形的三边之间是否有关系?
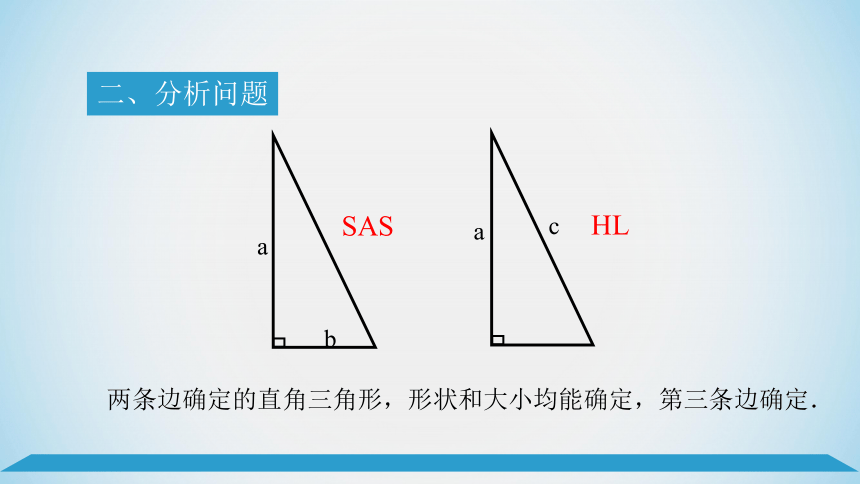
二、分析问题
a
b
a
c
两条边确定的直角三角形,形状和大小均能确定,第三条边确定.
SAS
HL
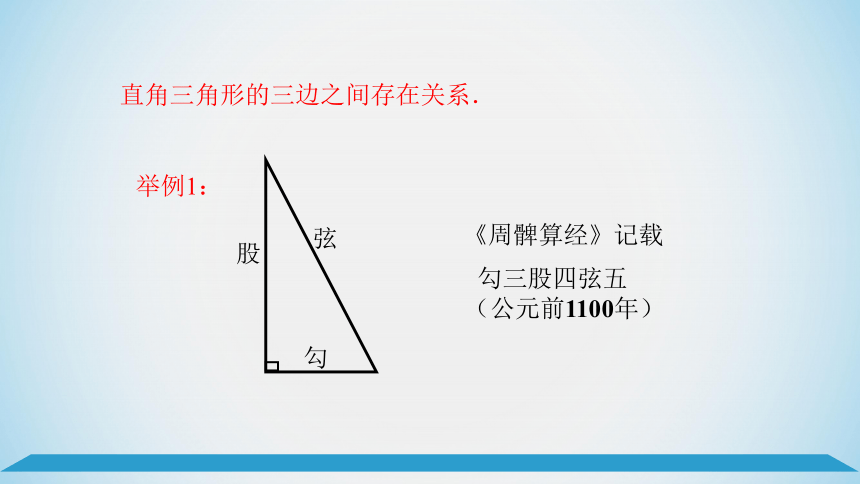
股
勾
弦
勾三股四弦五
(公元前1100年)
举例1:
《周髀算经》记载
直角三角形的三边之间存在关系.
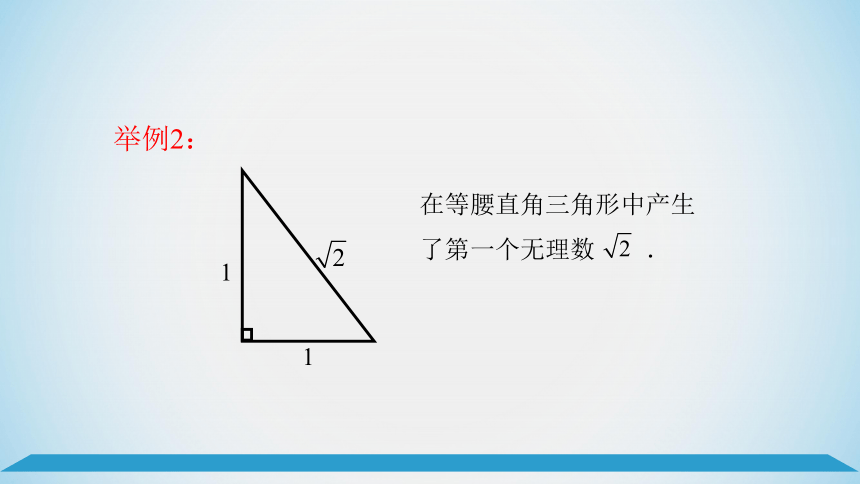
1
1
在等腰直角三角形中产生了第一个无理数 .
举例2:
直角三角形的三边之间是什么关系?
{5940675A-B579-460E-94D1-54222C63F5DA}a
b
c
3
4
5
5
12
13
…
当∠C=90°
关于三边的等式.
三、尝试探究
抽象 概括
…
勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
毕达哥拉斯( Pythagoras,约前580—约前500),古希腊著名的哲学家、数学家、天文学家.
等腰直角三角形三边之间存在数量关系.
猜想
一般直角三角形
验证
34
13
四、推理论证
命题1 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
a
b
c
正方形
面积
完全平
方公式
数
联想
a
b
c
C
B
A
∠C=90°
形
已知:Rt△ABC中,∠C=90°,
a,b,c分别是∠A,∠B,∠C的对边.
求证: .
a
b
c
C
B
A
边长为
a+b
边长
为c
长方形?
三角形?
数
形
联想
证法1
当∠C=90°时, .
a
b
a
b
c
数形
结合
b
b
a
a
90°
勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
角 边
证法2
赵爽弦图
按弦图,又可以勾股相乘为朱实二,倍之为朱实四.以勾股之差自相乘为中黄实.加差实,亦成弦实.
当∠C=90°时, .
证法3
当∠C=90°时, .
证法4
a
c
b
a
b
a
b
c
a
b
毕达哥拉斯证法
等积
变换
证法5
欧几里得证法
全等三角形面积相等;底和高分别相等的一对三角形面积相等.
△ADB≌△ACG
△BAG≌△BFC
当∠C=90°时, .
证法6
赵爽证法
课堂小结
勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
角 边
边 角?
数形结合
课后作业
1.设直角三角形两条直角边长分别为a和b,斜边长为c.
(1)已知a=3,c=4,求b;
(2)已知c=10,b=9,求a.
课后作业
2. 如图,图中所有的三角形都是直
角三角形,四边形都是正方形.
已知正方形A ,B,C,D的边长
分别是12,16,9,12,求最大正
方形E的面积.
再 见
学习目标
1
2
掌握勾股定理
了解关于勾股定理的一些文化历史背景,会用面积法来证明勾股定理
3
会用勾股定理进行简单的计算
学习重难点
重点
难点
掌握勾股定理
会用勾股定理进行简单的计算
一、提出问题
边 角
等角对等边
等边对等角
直角三角形的三边之间是否有关系?
二、分析问题
a
b
a
c
两条边确定的直角三角形,形状和大小均能确定,第三条边确定.
SAS
HL
股
勾
弦
勾三股四弦五
(公元前1100年)
举例1:
《周髀算经》记载
直角三角形的三边之间存在关系.
1
1
在等腰直角三角形中产生了第一个无理数 .
举例2:
直角三角形的三边之间是什么关系?
{5940675A-B579-460E-94D1-54222C63F5DA}a
b
c
3
4
5
5
12
13
…
当∠C=90°
关于三边的等式.
三、尝试探究
抽象 概括
…
勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
毕达哥拉斯( Pythagoras,约前580—约前500),古希腊著名的哲学家、数学家、天文学家.
等腰直角三角形三边之间存在数量关系.
猜想
一般直角三角形
验证
34
13
四、推理论证
命题1 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
a
b
c
正方形
面积
完全平
方公式
数
联想
a
b
c
C
B
A
∠C=90°
形
已知:Rt△ABC中,∠C=90°,
a,b,c分别是∠A,∠B,∠C的对边.
求证: .
a
b
c
C
B
A
边长为
a+b
边长
为c
长方形?
三角形?
数
形
联想
证法1
当∠C=90°时, .
a
b
a
b
c
数形
结合
b
b
a
a
90°
勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
角 边
证法2
赵爽弦图
按弦图,又可以勾股相乘为朱实二,倍之为朱实四.以勾股之差自相乘为中黄实.加差实,亦成弦实.
当∠C=90°时, .
证法3
当∠C=90°时, .
证法4
a
c
b
a
b
a
b
c
a
b
毕达哥拉斯证法
等积
变换
证法5
欧几里得证法
全等三角形面积相等;底和高分别相等的一对三角形面积相等.
△ADB≌△ACG
△BAG≌△BFC
当∠C=90°时, .
证法6
赵爽证法
课堂小结
勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
角 边
边 角?
数形结合
课后作业
1.设直角三角形两条直角边长分别为a和b,斜边长为c.
(1)已知a=3,c=4,求b;
(2)已知c=10,b=9,求a.
课后作业
2. 如图,图中所有的三角形都是直
角三角形,四边形都是正方形.
已知正方形A ,B,C,D的边长
分别是12,16,9,12,求最大正
方形E的面积.
再 见
