八年级下册17.1.2利用勾股定理求边长课件(配套)3(共33张ppt)
文档属性
| 名称 | 八年级下册17.1.2利用勾股定理求边长课件(配套)3(共33张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 07:24:17 | ||
图片预览











文档简介
17.1.2 勾股定理的基本应用
学习目标
1
2
掌握勾股定理去除实际背景在几何图形中的基本应用
掌握多个直角三角形组合应用勾股定理
3
掌握化斜三角形为直角三角形,化四边形为直角三角形等等问题
学习重难点
重点
难点
勾股定理去除实际背景在几何图形中的基本应用
勾股定理与方程思想的结合
勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
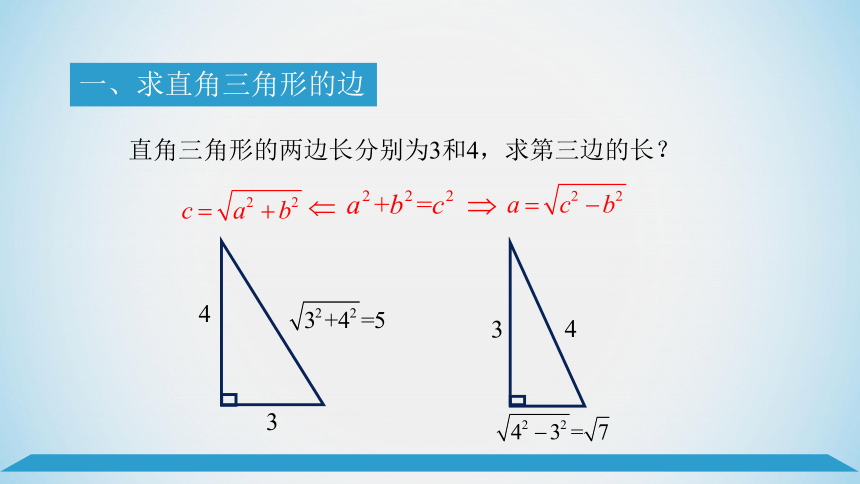
一、求直角三角形的边
直角三角形的两边长分别为3和4,求第三边的长?
4
3
3
4
勾股定理的结论与直角位置有关,因为它决定了边是斜边还是直角边.
位置 数量
归纳:
{5940675A-B579-460E-94D1-54222C63F5DA}a
b
c
1
?
2
1
2
?
2
3
?
2
4
?
2
3
算一算
位置 数量
已知两条直
角边长分别为a,
b,斜边长为c.
探一探
你能在数轴上画出表示 的点吗?
数形 结合
2
3
7
6
0
2
1
3
借助勾股定理可以画出许多无理数对应的长度.
借助勾股定理可以找到许多无理数在数轴上的位置.
5
条件二:有一条边是12;
条件一:另一条直角边是12;
位置 数量
已知直角三角形的一条直角边为5,请你补充一个条件,求得未知边.
求解直角三角形的一条边,一定需要已知两边长吗?
想一想
条件三:有一锐角是30°;
5
10
30°
30°
x
5
2x
已知直角三角形的一条直角边为5,请你补充一个条件,求得未知边.
勾股定理是一个关于直角三角形三边的等式,当其中存在未知边时,这就是一个方程.
归纳:
已知直角三角形的一条直角边为5,请你补充一个条件,求得未知边.
条件四:另外两条边之差为1;
条件五:周长为30.
方程思想
消
元
条件六:三条边长恰好为三个连续整数.
情况一:已知两边;
情况二:已知一边,以及两边的关系.
直角三角形中边的计算
情况三:已知三边之间的关系.
一元方程
消元
归纳:
10
12
10
已知等腰三角形的一条腰为10,底为12,求这个等腰三角形的面积.
6
8
二、求三角形中的重要线段
10
12
10
已知等腰三角形的一条腰为10,底为12,求这个等腰三角形一腰上的高.
一个确定的图形所有元素都是确定的.
6
8
h
已知Rt△ABC中,∠C=90°,AC=3,BC=4 ,AD是△ABC的角平分线,求AD.
4
3
C
B
A
D
h
H
法一:
作DH⊥AB于H,由角平分线性质DH=DC.
AD=
Rt△ACD中
3
作DH⊥AB于H,
由轴对称得DH=DC,AH=AC.
法二:
Rt△BDH中
3
2
4-h
4
C
B
A
D
h
H
已知Rt△ABC中,∠C=90°,AC=3,BC=4 ,AD是△ABC的角平分线,求AD.
A
B
C
已知△ABC中,AB= ,AC= ,BC=12,AD是△ABC的中线,求AD.
D
H
12
Rt△ACH中知AC.
已知BH+CH=12
Rt△ADH中
知AH,DH.
Rt△ABH
中知AB.
AH=AH
CH=12-x
BH=x
Rt△ACH中知AC.
AH=AH
Rt△ABH
中知AB.
A
B
C
D
H
Rt△ABH中
AB = ,BH=4.
Rt△ADH中
AH=4,DH=2.
AH=4
AH=BH
∠B=45°
A
B
C
D
H
斜三角形中线段
转 化
直角三角形的边
归纳:
将几何图形的性质数量化
消 元
建立关于未知线段的方程
归纳:
10
12
已知等腰三角形的一条腰为10,底为12,求这个等腰三角形一腰上的高.
h
x
10-x
已知四边形 ABCD中,AB=BC =12,∠ABC=∠ACD=90°,CD= ,求BD的长.
三、求其它多边形中的线段
C
A
B
D
三角形的边
转化
直角三角形的边
12
12
C
A
B
12
45°
H
四边形 ABCD
△BCD
Rt△BDH
与Rt△BCH
12
A
D
H
P
C
B
12
12
几何图形
三角形
直角三角形
勾股定理
图形性质
方程思想
位置 数量
数形结合
图形计算
课堂总结
课后作业
1.如图,Rt△ABC中,∠C=90°,∠A=30°,AC=2,求斜边AB长.
B
C
A
30°
课后作业
2.如图,等边三角形 的边长是6.求这个 三角形的面积.
A
B
C
再 见
学习目标
1
2
掌握勾股定理去除实际背景在几何图形中的基本应用
掌握多个直角三角形组合应用勾股定理
3
掌握化斜三角形为直角三角形,化四边形为直角三角形等等问题
学习重难点
重点
难点
勾股定理去除实际背景在几何图形中的基本应用
勾股定理与方程思想的结合
勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么 .
一、求直角三角形的边
直角三角形的两边长分别为3和4,求第三边的长?
4
3
3
4
勾股定理的结论与直角位置有关,因为它决定了边是斜边还是直角边.
位置 数量
归纳:
{5940675A-B579-460E-94D1-54222C63F5DA}a
b
c
1
?
2
1
2
?
2
3
?
2
4
?
2
3
算一算
位置 数量
已知两条直
角边长分别为a,
b,斜边长为c.
探一探
你能在数轴上画出表示 的点吗?
数形 结合
2
3
7
6
0
2
1
3
借助勾股定理可以画出许多无理数对应的长度.
借助勾股定理可以找到许多无理数在数轴上的位置.
5
条件二:有一条边是12;
条件一:另一条直角边是12;
位置 数量
已知直角三角形的一条直角边为5,请你补充一个条件,求得未知边.
求解直角三角形的一条边,一定需要已知两边长吗?
想一想
条件三:有一锐角是30°;
5
10
30°
30°
x
5
2x
已知直角三角形的一条直角边为5,请你补充一个条件,求得未知边.
勾股定理是一个关于直角三角形三边的等式,当其中存在未知边时,这就是一个方程.
归纳:
已知直角三角形的一条直角边为5,请你补充一个条件,求得未知边.
条件四:另外两条边之差为1;
条件五:周长为30.
方程思想
消
元
条件六:三条边长恰好为三个连续整数.
情况一:已知两边;
情况二:已知一边,以及两边的关系.
直角三角形中边的计算
情况三:已知三边之间的关系.
一元方程
消元
归纳:
10
12
10
已知等腰三角形的一条腰为10,底为12,求这个等腰三角形的面积.
6
8
二、求三角形中的重要线段
10
12
10
已知等腰三角形的一条腰为10,底为12,求这个等腰三角形一腰上的高.
一个确定的图形所有元素都是确定的.
6
8
h
已知Rt△ABC中,∠C=90°,AC=3,BC=4 ,AD是△ABC的角平分线,求AD.
4
3
C
B
A
D
h
H
法一:
作DH⊥AB于H,由角平分线性质DH=DC.
AD=
Rt△ACD中
3
作DH⊥AB于H,
由轴对称得DH=DC,AH=AC.
法二:
Rt△BDH中
3
2
4-h
4
C
B
A
D
h
H
已知Rt△ABC中,∠C=90°,AC=3,BC=4 ,AD是△ABC的角平分线,求AD.
A
B
C
已知△ABC中,AB= ,AC= ,BC=12,AD是△ABC的中线,求AD.
D
H
12
Rt△ACH中知AC.
已知BH+CH=12
Rt△ADH中
知AH,DH.
Rt△ABH
中知AB.
AH=AH
CH=12-x
BH=x
Rt△ACH中知AC.
AH=AH
Rt△ABH
中知AB.
A
B
C
D
H
Rt△ABH中
AB = ,BH=4.
Rt△ADH中
AH=4,DH=2.
AH=4
AH=BH
∠B=45°
A
B
C
D
H
斜三角形中线段
转 化
直角三角形的边
归纳:
将几何图形的性质数量化
消 元
建立关于未知线段的方程
归纳:
10
12
已知等腰三角形的一条腰为10,底为12,求这个等腰三角形一腰上的高.
h
x
10-x
已知四边形 ABCD中,AB=BC =12,∠ABC=∠ACD=90°,CD= ,求BD的长.
三、求其它多边形中的线段
C
A
B
D
三角形的边
转化
直角三角形的边
12
12
C
A
B
12
45°
H
四边形 ABCD
△BCD
Rt△BDH
与Rt△BCH
12
A
D
H
P
C
B
12
12
几何图形
三角形
直角三角形
勾股定理
图形性质
方程思想
位置 数量
数形结合
图形计算
课堂总结
课后作业
1.如图,Rt△ABC中,∠C=90°,∠A=30°,AC=2,求斜边AB长.
B
C
A
30°
课后作业
2.如图,等边三角形 的边长是6.求这个 三角形的面积.
A
B
C
再 见
