2020-2021学年苏科版七年级数学下册 第7章 平面图形的认识(二)章末解答题突破训练(一)(word版含解析)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册 第7章 平面图形的认识(二)章末解答题突破训练(一)(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 214.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-21 00:00:00 | ||
图片预览


文档简介
七年级数学下册
第7章
平面图形的认识(二)
章末解答题突破训练(一)
1.已知AB∥CD.
(1)如图1,EOF是直线AB、CD间的一条折线,猜想∠1、∠2、∠3的数量关系,并说明理由;
(2)如图2,若点C在点D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DF所在直线交于点E,若∠ADC=α,∠ABC=β,求∠BED的度数(用含有α、β的式子表示);
(3)在(2)的前提下将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,若∠ADC=α,∠ABC=β,求∠BED的度数(用含有α、β的式子表示).
2.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°).
(1)如图1,①若∠DCE=40°,求∠ACB的度数;
②若∠ACB=150°,直接写出∠DCE的度数是
度.
(2)由(1)猜想∠ACB与∠DCE满足的数量关系是
.
(3)若固定△ACD,将△BCE绕点C旋转,
①当旋转至BE∥AC(如图2)时,直接写出∠ACE的度数是
度.
②继续旋转至BC∥DA(如图3)时,求∠ACE的度数.
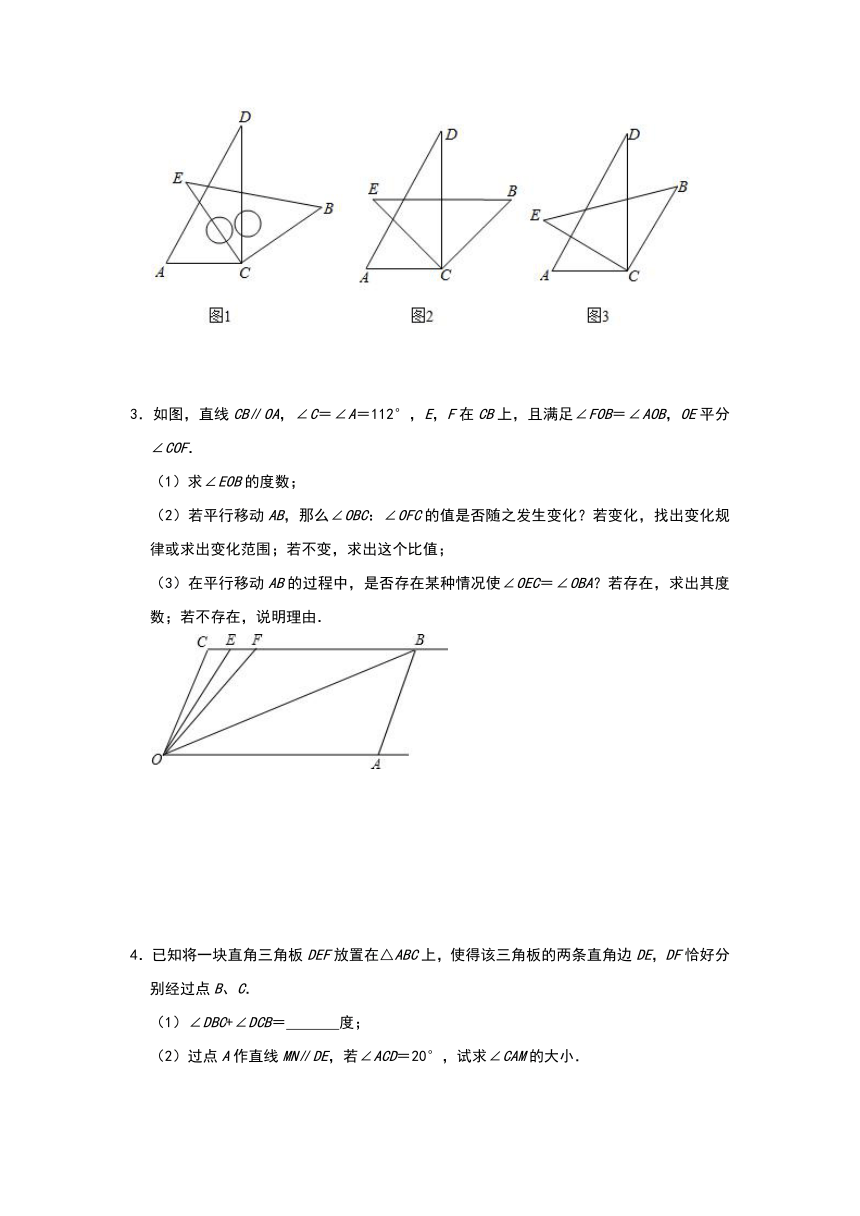
3.如图,直线CB∥OA,∠C=∠A=112°,E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
4.已知将一块直角三角板DEF放置在△ABC上,使得该三角板的两条直角边DE,DF恰好分别经过点B、C.
(1)∠DBC+∠DCB=
度;
(2)过点A作直线MN∥DE,若∠ACD=20°,试求∠CAM的大小.
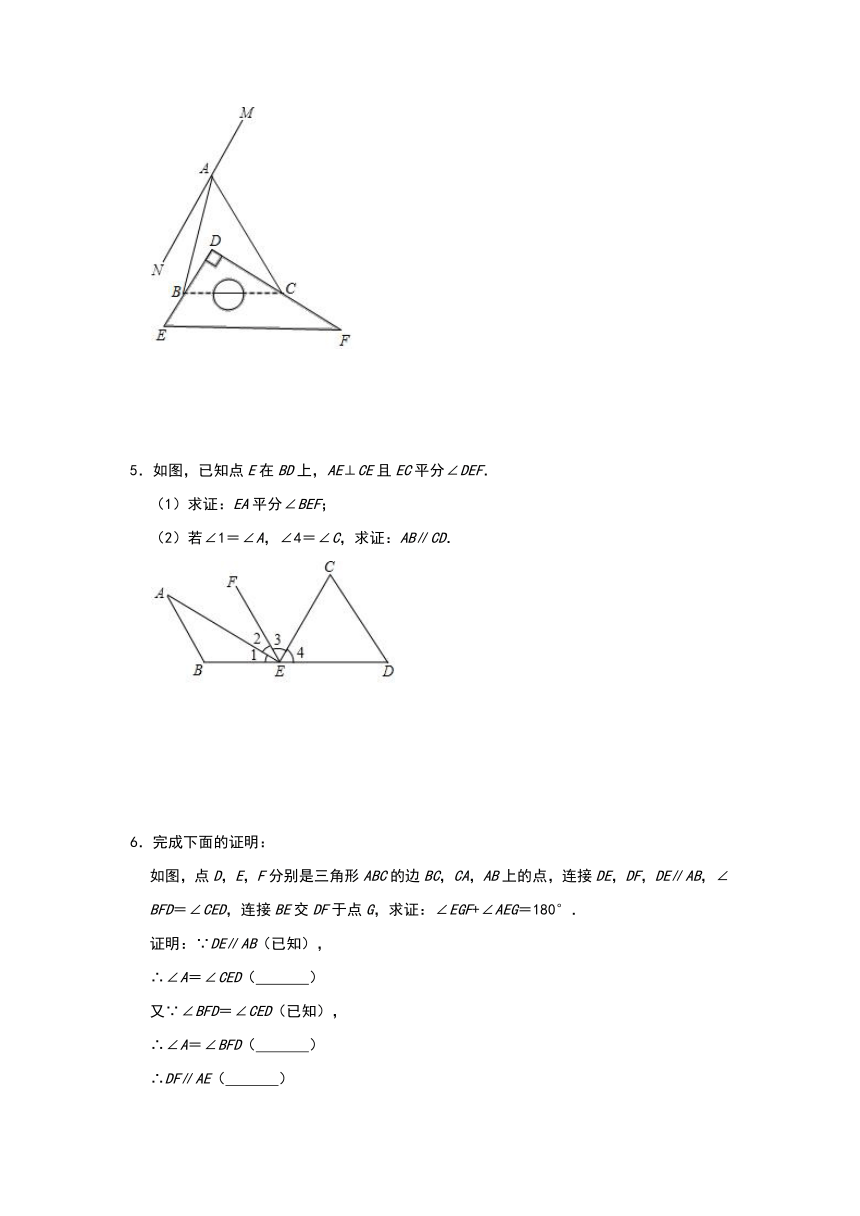
5.如图,已知点E在BD上,AE⊥CE且EC平分∠DEF.
(1)求证:EA平分∠BEF;
(2)若∠1=∠A,∠4=∠C,求证:AB∥CD.
6.完成下面的证明:
如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE∥AB(已知),
∴∠A=∠CED(
)
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD(
)
∴DF∥AE(
)
∴∠EGF+∠AEG=180°(
)
7.若∠C=α,∠EAC+∠FBC=β.
(1)如图1,若AE∥BF,则α与β有何关系?
(直接写出结果);
(2)如图2,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,判断α与β的关系,并说明理由;
(3)若∠EAC的平分线与∠FBC平分线交于点P,试探究∠APB与α、β的关系
(直接写出结果,用含α、β的代数式表示∠APB);
(4)如图3,若α≥β,∠EAC与∠FBC的平分线相交于P1,∠EAP1与∠FBP1的平分线交于P2…依此类推,则∠P4=
(用含α、β的代数式表示);∠Pn=
(n是整数,且n≥2,用含α、β、n的代数式表示).
8.(1)①如图1,已知AB∥CD,∠ABC=60°,根据
可得∠BCD=
°;
②如图2,在①的条件下,如果CM平分∠BCD,则∠BCM=
°;
③如图3,在①、②的条件下,如果CN⊥CM,则∠BCN=
°.
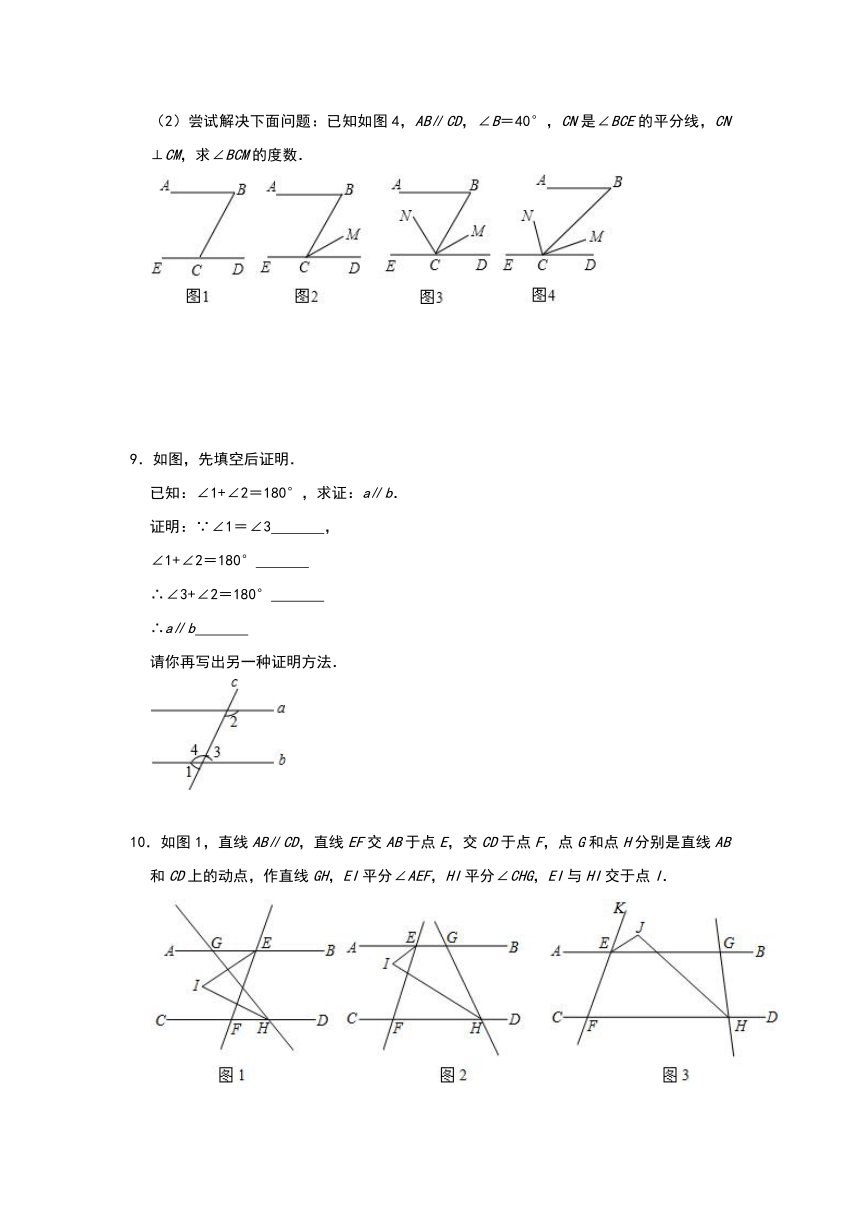
(2)尝试解决下面问题:已知如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线,CN⊥CM,求∠BCM的度数.
9.如图,先填空后证明.
已知:∠1+∠2=180°,求证:a∥b.
证明:∵∠1=∠3
,
∠1+∠2=180°
∴∠3+∠2=180°
∴a∥b
请你再写出另一种证明方法.
10.如图1,直线AB∥CD,直线EF交AB于点E,交CD于点F,点G和点H分别是直线AB和CD上的动点,作直线GH,EI平分∠AEF,HI平分∠CHG,EI与HI交于点I.
(1)如图1,点G在点E的左侧,点H在点F的右侧,若∠AEF=70°,∠CHG=60°,求∠EIH的度数.
(2)如图2,点G在点E的右侧,点H也在点F的右侧,若∠AEF=α,∠CHG=β,其他条件不变,求∠EIH的度数.
(3)如图3,点G在点E的右侧,点H也在点F的右侧,∠GHC的平分线HJ交∠KEG的平分线EJ于点J.其他条件不变,若∠AEF=α,∠CHG=β,求∠EJH的度数.
11.探究:如图①,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,若∠ABC=50°,求∠DEF的度数.
请将下面的解答过程补充完整,并填空
解:∵DE∥BC
∴∠DEF=
.(
)
∵EF∥AB,
∴
=∠ABC.(
)
∴∠DEF=∠ABC.(等量代换)
∵∠ABC=50°,
∴∠DEF=
.
应用:如图②,直线AB,BC,AC两两相交,交点分别为A、B、C,点D在线段AB的延长线上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,若∠ABC=65°,则∠DEF=
.
12.如图,将三角形ABC沿射线BA方向平移到三角形A′B′C′的位置,连接AC′.
(1)AA′与CC′的位置关系为
;
(2)求证:∠A′+∠CAC′+∠AC′C=180°;
(3)设∠AC′B′=x,∠ACB=y,试探索∠CAC′与x,y之间的数量关系,并证明你的结论.
13.如图,直线MA∥NB.
(1)如图1,你能得到∠APB=∠A+∠B这个结论正确吗?并说明你的理由;
(2)如图2,请直接写出∠A,∠B,∠P1,∠P2,∠P3之间的关系
.
(3)如图3,请直接写出∠A,∠B,∠P1……∠P2n+1之间的关系
.
14.长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图2,灯A射线自AM顺时针旋转至AN便立即回转至原位置,灯B射线自BP顺时针旋转至BQ便立即回转至原位置,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a﹣3|+(a+b﹣4)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°.
(1)求a、b的值.
(2)如图1,若两灯同时转动,在灯A射线第一次转到AN之前,两灯射出的光线交于点C,若∠C=70°,求∠BAC的度数.
(3)若灯B射线先转动20秒,灯A射线才开始转动,在灯B射线第一次转到BQ之前,A灯转动几秒,两灯的光线互相平行?
15.(1)如图1,AB∥CD,∠AEP=40°,∠PFD=130°.求∠EPF的度数.
小明想到了以下方法(不完整),请填写以下结论的依据:
如图1,过点P作PM∥AB,
∴∠1=∠AEP=40°(
)
∵AB∥CD,(已知)
∴PM∥CD,(
)
∴∠2+∠PFD=180°.(
)
∵∠PFD=130°,∴∠2=180°﹣130°=50°.
∴∠1+∠2=40°+50°=90°.
即∠EPF=90°.
(2)如图2,AB∥CD,点P在AB,CD外,问∠PEA,∠PFC,∠P之间有何数量关系?请说明理由;
(3)如图3所示,在(2)的条件下,已知∠P=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数是
.(直接写出答案,不需要写出过程)
参考答案
1.解:(1)如图1,过O作OM∥AB,
∵AB∥CD,
∴AB∥CD∥0M,
∴∠1=∠EOM,∠3=∠FOM,
∵∠EOF=∠EOM+∠FOM,
∴∠2=∠1+∠3,
(2)如图2,过E作EN∥AB,则EN∥AB∥CD,
∴∠BEN=∠ABE,∠DEN=∠CDE
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠EBC=∠ABC,∠ADE=∠CDE=∠ADC,
∴∠BED=∠ABE+∠CDE=α+β,
答:∠BED=α+β,
(3)如图3,过E作EP∥AB,则EP∥AB∥CD,
∴∠PED=∠EDC,∠PEB+∠ABE=180°,
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠EBC=∠ABC,∠ADE=∠CDE=∠ADC,
∴∠BED=∠PED+∠PEB=α+(180°﹣β)
=α﹣β+180°,
答:∠BED=α﹣β+180°.
2.解:(1)
①∵∠DCE=40°,
∴∠ACE=∠ACD﹣∠DCE=50°,
∴∠ACB=∠ACE+∠ECB=50°+90°=140°;
②∵∠ACB=150°,∠ACD=90°,
∴∠ACE=150°﹣90°=60°,
∴∠DCE=∠ACD﹣∠ACE=90°﹣60°=30°,
故答案为:30;
(2)∵∠ACB=∠ACD+∠BCE﹣∠DCE=90°+90°﹣∠DCE,
∴∠ACB+∠DCE=180°,
故答案为:∠ACB+∠DCE=180°;
(3)①∵BE∥AC,
∴∠ACE=∠E=45°,
故答案为:45°;
②∵BC∥DA,
∴∠A+∠ACB=180°,
又∵∠A=60°,
∴∠ACB=180°﹣60°=120°,
∵∠BCE=90°,
∴∠BCD=∠ACB﹣∠ECB=120°﹣90°=30°.
3.解:(1)∵CB∥OA,
∴∠AOC=180°﹣∠C=180°﹣112°=68°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=∠AOC=×68°=34°;
(2)∠OBC:∠OFC的值不变.
∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=∠AOC=×68°=17°,
∴∠OEC=180°﹣∠C﹣∠COE=180°﹣112°﹣17°=51°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=51°.
4.解:(1)在△DBC中,∵∠DBC+∠DCB+∠D=180°,
而∠D=90°,
∴∠DBC+∠DCB=90°;
故答案为90;
(2)在△ABC中,
∵∠ABC+∠ACB+∠A=180°,
即∠ABD+∠DBC+∠DCB+∠ACD+∠BAC=180°,
而∠DBC+∠DCB=90°,
∴∠ABD+∠ACD=90°﹣∠BAC,
∴∠ABD+∠BAC=90°﹣∠ACD=70°.
又∵MN∥DE,
∴∠ABD=∠BAN.
而∠BAN+∠BAC+∠CAM=180°,
∴∠ABD+∠BAC+∠CAM=180°,
∴∠CAM=180°﹣(∠ABD+∠BAC)=110°.
5.证明:(1)∵AE⊥CE,
∴∠AEC=90°,
∴∠2+∠3=90°且∠1+∠4=90°,
又∵EC平分∠DEF,
∴∠3=∠4,
∴∠1=∠2,
∴EA平分∠BEF;
(2)∵∠1=∠A,∠4=∠C,
∴∠1+∠A+∠4+∠C=2(∠1+∠4)=180°,
∴∠B+∠D=(180°﹣2∠1)+(180°﹣2∠4)=360°﹣2(∠1+∠4)=180°,
∴AB∥CD.
6.证明:∵DE∥AB(已知),
∴∠A=∠CED(两直线平行,同位角相等)
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD(等量代换)
∴DF∥AE(同位角相等,两直线平行)
∴∠EGF+∠AEG=180°(两直线平行,同旁内角互补)
故答案为:两直线平行,同位角相等;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补.
7.解:(1)过点C作CM∥AE,如答图1所示.
∵CM∥AE,
∴∠EAC=∠ACM.
∵CM∥AE,AE∥BF,
∴CM∥BF,
∴∠FBC=∠BCM.
∵∠ACB=∠ACM+∠BCM=α,∠EAC+∠FBC=β,
∴α=β.
故答案为:α=β.
(2)α=β.理由如下:
过点C作CG∥AM,如答图2所示.
∵CG∥AM,AM∥BN,
∴AM∥BN∥CG,
∴∠MAC=∠ACG,∠NBC=∠BCG,
∵AM是∠EAC的平分线,BN是∠FBC的平分线,
∴∠ACB=∠ACG+∠BCG=∠MAC+∠NBC=∠EAC+∠FBC=(∠EAC+∠FBC)=β.
(3)连接PC并延长到点M,如答图3所示.
∵∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,
∴∠PAC=∠EAC,∠PBC=∠FBC,
∵∠ACM=∠PAC+∠APC,∠BCM=∠PBC+∠BPC,∠ACB=∠ACM+∠BCM,∠APB=∠APC+∠BPC,
∴∠ACB=∠PAC+∠PBC+∠APB,
∵∠ACB=α,∠EAC+∠FBC=β,
∴α=β+∠APB,
∴∠APB=α﹣β.
故答案为:∠APB=α﹣β.
(4)结合(3)结论可知:∠P1=α﹣β,∠P2=α﹣β,∠P3=α﹣β,
∴∠P4=α﹣β,…
∴∠Pn=α﹣β.
故答案为:α﹣β,α﹣β.
8.解:(1)①两直线平行,内错角相等;60;
②30;
③60.
(2)∵AB∥CD,
∴∠B+∠BCE=180°,
∵∠B=40°,
∴∠BCE=180°﹣∠B=180°﹣40°=140°.
又∵CN是∠BCE的平分线,
∴∠BCN=140°÷2=70°.
∵CN⊥CM,
∴∠BCM=90°﹣∠BCN=90°﹣70°=20°.
9.证明:∵∠1=∠3
对顶角相等,
∠1+∠2=180°
已知,
∴∠3+∠2=180°
等量代换,
∴a∥b
同旁内角互补,两直线平行.
故答案为:对顶角相等;已知;等量代换;同旁内角互补,两直线平行.
另一种证法:
∵∠1+∠2=180°,∠1+∠4=180°,
∴∠2=∠4,
∴a∥b.
10.(1)解:如图1,过点I作IM∥AB,
∵EI平分∠AEF,HI平分∠CHG,∠AEF=70°,∠CHG=60°,
∴∠AEI=35°,∠CHI=30°,
∵IM∥AB,
∴∠MIE=∠AEI=35°,
∵AB∥CD,IM∥AB,
∴IM∥CD,
∴∠MIH=∠CHI=30°,
∴∠EIH=∠MIE+∠MIH=35°+30°=65°;
(2)解:如图2,过点I作IM∥AB,
∵EI平分∠AEF,HI平分∠CHG,∠AEF=α,∠CHG=β,
∴∠AEI=,∠CHI=,
∵IM∥AB,
∴∠MIE=∠AEI=,
∵AB∥CD,IM∥AB,
∴IM∥CD,
∴∠MIH=∠CHI=,
∴∠EIH=∠MIE+∠MIH=+;
(3)解:如图3,过点J作MN∥AB,
∵∠AEF=α,
∴∠KEB=α,
∵EJ平分∠KEB,HJ平分∠CHG,∠KEB=α,∠CHG=β,
∴∠JEG=,∠JHF=,
∵MN∥AB,
∴∠MJE=∠JEG=,
∵AB∥CD,MN∥AB,
∴MN∥CD,
∴∠NJH=∠CHJ=,
∴∠EJH=180°﹣∠MJE﹣∠NJH=180°﹣﹣.
11.解:探究:∵DE∥BC,
∴∠DEF=∠EFC.(两直线平行,内错角相等)
∵EF∥AB,
∴∠EFC=∠ABC.(两直线平行,同位角相等)
∴∠DEF=∠ABC.(等量代换)
∵∠ABC=50°,
∴∠DEF=50°.
故答案为:∠EFC,两直线平行,内错角相等,∠EFC,两直线平行,同位角相等,50°;
应用:∵DE∥BC,
∴∠ABC=∠ADE=60°.(两直线平行,同位角相等)
∵EF∥AB,
∴∠ADE+∠DEF=180°.(两直线平行,同旁内角互补)
∴∠DEF=180°﹣65°=115°.
故答案为:115°.
12.解:(1)由平移的性质可得:AA′∥CC′;
故答案为:AA′∥CC′;
(2)根据平移性质可知A'C'∥AC,AA'∥CC',
∴∠A'=∠BAC,∠BAC=∠ACC',
∴∠A'=∠ACC',
∵∠ACC'+∠CAC′+∠AC′C=180°,
∴∠A'+∠CAC'+∠AC'C=180°,
(3)结论:∠CAC'=x+y,
过点A作AD∥BC,交CC'于点D,
根据平移性质可知B'C'∥BC,
∴B'C'∥AD∥BC',
∴∠AC'B'=∠C'AD,∠ACB=∠DAC,
∴∠CAC'=∠C'AD+∠CAD=∠AC'B'+∠ACB=x+y,
即∠CAC'=x+y.
13.证明:(1)∠APB=∠A+∠B这个结论正确,理由如下
如图1,过点P作PQ∥AM,
∵PQ∥AM,AM∥BN,
∴PQ∥AM∥BN,
∴∠A=∠APQ,∠B=∠BPQ,
∴∠A+∠B=∠APQ+∠BPQ=∠APB,
即:∠APB=∠A+∠B.
(2)根据(1)中结论可得,∠A+∠B+∠P2=∠P1+∠P3,
故答案为:∠A+∠B+∠P2=∠P1+∠P3,
(3)由(2)的规律得,∠A+∠B+∠P2+…+P2n=∠P1+∠P3+∠P5+…+∠P2n+1
故答案为:∠A+∠B+∠P2+…+P2n=∠P1+∠P3+∠P5+…+∠P2n+1
14.解:(1)∵|a﹣3|+(a+b﹣4)2=0,
∴a﹣3=0,a+b﹣4=0,
解得:a=3,b=1;
(2)如图1,过点C作CE∥MN,
∵PQ∥MN,
∴CE∥PQ∥MN,
设两灯转动时间为x秒,则∠MAC=3x°,∠PBC=x°,
∴∠CAN=180°﹣3x°,
∴∠BCE=∠PBC=x°,∠ECA=∠CAN=(180﹣3x)°,
∵∠ACB=70°,
∴180﹣3x+x=70,
解得x=55,
∴∠CAN=15°,
∴∠BAC=∠BAN﹣∠CAN=45°﹣15°=30°;
(3)设A灯转动t秒,两灯的光束互相平行,
①在灯A射线到达AN之前,由题意得:3t=(20+t)×1,
解得:t=10;
②在灯A射线到达AN之后,由题意得:3t﹣180=180﹣(20+t)×1,
解得:t=85.
综上所述,A灯转动10秒或85秒时,两灯的光束互相平行.
15.解:(1)如图1,过点P作PM∥AB,
∴∠1=∠AEP=40°.(两直线平行,内错角相等)
∵AB∥CD,(已知)
∴PM∥CD,(平行于同一条直线的两直线平行)
∴∠2+∠PFD=180°.
(两直线平行,同旁内角互补)
∵∠PFD=130°,
∴∠2=180°﹣130°=50°.
∴∠1+∠2=40°+50°=90°.
即∠EPF=90°.
故答案为:两直线平行,内错角相等;平行于同一条直线的两直线平行;两直线平行,同旁内角互补;
(2)∠PFC=∠PEA+∠P.
理由:如图2,过P点作PN∥AB,则PN∥CD,
∴∠PEA=∠NPE,
∵∠FPN=∠NPE+∠FPE,
∴∠FPN=∠PEA+∠FPE,
∵PN∥CD,
∴∠FPN=∠PFC,
∴∠PFC=∠PEA+∠FPE,即∠PFC=∠PEA+∠P;
(3)令AB与PF交点为O,连接EF,如图3.
在△GFE中,∠G=180°﹣(∠GFE+∠GEF),
∵∠GEF=PEA+∠OEF,∠GFE=PFC+∠OFE,
∴∠GEF+∠GFE=PEA+∠OEF+PFC+∠OFE,
∵由(2)知∠PFC=∠PEA+∠P,
∴∠PEA=∠PFC﹣α,
∵∠OFE+∠OEF=180°﹣∠FOE=180°﹣∠PFC,
∴∠GEF+∠GFE=(∠PFC﹣α)+∠PFC+180°﹣∠PFC=180°﹣α,
∴∠G=180°﹣(∠GEF+∠GFE)=180°﹣180°+α=α.
故答案为:α.
第7章
平面图形的认识(二)
章末解答题突破训练(一)
1.已知AB∥CD.
(1)如图1,EOF是直线AB、CD间的一条折线,猜想∠1、∠2、∠3的数量关系,并说明理由;
(2)如图2,若点C在点D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DF所在直线交于点E,若∠ADC=α,∠ABC=β,求∠BED的度数(用含有α、β的式子表示);
(3)在(2)的前提下将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,若∠ADC=α,∠ABC=β,求∠BED的度数(用含有α、β的式子表示).
2.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°).
(1)如图1,①若∠DCE=40°,求∠ACB的度数;
②若∠ACB=150°,直接写出∠DCE的度数是
度.
(2)由(1)猜想∠ACB与∠DCE满足的数量关系是
.
(3)若固定△ACD,将△BCE绕点C旋转,
①当旋转至BE∥AC(如图2)时,直接写出∠ACE的度数是
度.
②继续旋转至BC∥DA(如图3)时,求∠ACE的度数.
3.如图,直线CB∥OA,∠C=∠A=112°,E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
4.已知将一块直角三角板DEF放置在△ABC上,使得该三角板的两条直角边DE,DF恰好分别经过点B、C.
(1)∠DBC+∠DCB=
度;
(2)过点A作直线MN∥DE,若∠ACD=20°,试求∠CAM的大小.
5.如图,已知点E在BD上,AE⊥CE且EC平分∠DEF.
(1)求证:EA平分∠BEF;
(2)若∠1=∠A,∠4=∠C,求证:AB∥CD.
6.完成下面的证明:
如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE∥AB(已知),
∴∠A=∠CED(
)
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD(
)
∴DF∥AE(
)
∴∠EGF+∠AEG=180°(
)
7.若∠C=α,∠EAC+∠FBC=β.
(1)如图1,若AE∥BF,则α与β有何关系?
(直接写出结果);
(2)如图2,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,判断α与β的关系,并说明理由;
(3)若∠EAC的平分线与∠FBC平分线交于点P,试探究∠APB与α、β的关系
(直接写出结果,用含α、β的代数式表示∠APB);
(4)如图3,若α≥β,∠EAC与∠FBC的平分线相交于P1,∠EAP1与∠FBP1的平分线交于P2…依此类推,则∠P4=
(用含α、β的代数式表示);∠Pn=
(n是整数,且n≥2,用含α、β、n的代数式表示).
8.(1)①如图1,已知AB∥CD,∠ABC=60°,根据
可得∠BCD=
°;
②如图2,在①的条件下,如果CM平分∠BCD,则∠BCM=
°;
③如图3,在①、②的条件下,如果CN⊥CM,则∠BCN=
°.
(2)尝试解决下面问题:已知如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线,CN⊥CM,求∠BCM的度数.
9.如图,先填空后证明.
已知:∠1+∠2=180°,求证:a∥b.
证明:∵∠1=∠3
,
∠1+∠2=180°
∴∠3+∠2=180°
∴a∥b
请你再写出另一种证明方法.
10.如图1,直线AB∥CD,直线EF交AB于点E,交CD于点F,点G和点H分别是直线AB和CD上的动点,作直线GH,EI平分∠AEF,HI平分∠CHG,EI与HI交于点I.
(1)如图1,点G在点E的左侧,点H在点F的右侧,若∠AEF=70°,∠CHG=60°,求∠EIH的度数.
(2)如图2,点G在点E的右侧,点H也在点F的右侧,若∠AEF=α,∠CHG=β,其他条件不变,求∠EIH的度数.
(3)如图3,点G在点E的右侧,点H也在点F的右侧,∠GHC的平分线HJ交∠KEG的平分线EJ于点J.其他条件不变,若∠AEF=α,∠CHG=β,求∠EJH的度数.
11.探究:如图①,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,若∠ABC=50°,求∠DEF的度数.
请将下面的解答过程补充完整,并填空
解:∵DE∥BC
∴∠DEF=
.(
)
∵EF∥AB,
∴
=∠ABC.(
)
∴∠DEF=∠ABC.(等量代换)
∵∠ABC=50°,
∴∠DEF=
.
应用:如图②,直线AB,BC,AC两两相交,交点分别为A、B、C,点D在线段AB的延长线上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,若∠ABC=65°,则∠DEF=
.
12.如图,将三角形ABC沿射线BA方向平移到三角形A′B′C′的位置,连接AC′.
(1)AA′与CC′的位置关系为
;
(2)求证:∠A′+∠CAC′+∠AC′C=180°;
(3)设∠AC′B′=x,∠ACB=y,试探索∠CAC′与x,y之间的数量关系,并证明你的结论.
13.如图,直线MA∥NB.
(1)如图1,你能得到∠APB=∠A+∠B这个结论正确吗?并说明你的理由;
(2)如图2,请直接写出∠A,∠B,∠P1,∠P2,∠P3之间的关系
.
(3)如图3,请直接写出∠A,∠B,∠P1……∠P2n+1之间的关系
.
14.长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图2,灯A射线自AM顺时针旋转至AN便立即回转至原位置,灯B射线自BP顺时针旋转至BQ便立即回转至原位置,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a﹣3|+(a+b﹣4)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°.
(1)求a、b的值.
(2)如图1,若两灯同时转动,在灯A射线第一次转到AN之前,两灯射出的光线交于点C,若∠C=70°,求∠BAC的度数.
(3)若灯B射线先转动20秒,灯A射线才开始转动,在灯B射线第一次转到BQ之前,A灯转动几秒,两灯的光线互相平行?
15.(1)如图1,AB∥CD,∠AEP=40°,∠PFD=130°.求∠EPF的度数.
小明想到了以下方法(不完整),请填写以下结论的依据:
如图1,过点P作PM∥AB,
∴∠1=∠AEP=40°(
)
∵AB∥CD,(已知)
∴PM∥CD,(
)
∴∠2+∠PFD=180°.(
)
∵∠PFD=130°,∴∠2=180°﹣130°=50°.
∴∠1+∠2=40°+50°=90°.
即∠EPF=90°.
(2)如图2,AB∥CD,点P在AB,CD外,问∠PEA,∠PFC,∠P之间有何数量关系?请说明理由;
(3)如图3所示,在(2)的条件下,已知∠P=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数是
.(直接写出答案,不需要写出过程)
参考答案
1.解:(1)如图1,过O作OM∥AB,
∵AB∥CD,
∴AB∥CD∥0M,
∴∠1=∠EOM,∠3=∠FOM,
∵∠EOF=∠EOM+∠FOM,
∴∠2=∠1+∠3,
(2)如图2,过E作EN∥AB,则EN∥AB∥CD,
∴∠BEN=∠ABE,∠DEN=∠CDE
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠EBC=∠ABC,∠ADE=∠CDE=∠ADC,
∴∠BED=∠ABE+∠CDE=α+β,
答:∠BED=α+β,
(3)如图3,过E作EP∥AB,则EP∥AB∥CD,
∴∠PED=∠EDC,∠PEB+∠ABE=180°,
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠EBC=∠ABC,∠ADE=∠CDE=∠ADC,
∴∠BED=∠PED+∠PEB=α+(180°﹣β)
=α﹣β+180°,
答:∠BED=α﹣β+180°.
2.解:(1)
①∵∠DCE=40°,
∴∠ACE=∠ACD﹣∠DCE=50°,
∴∠ACB=∠ACE+∠ECB=50°+90°=140°;
②∵∠ACB=150°,∠ACD=90°,
∴∠ACE=150°﹣90°=60°,
∴∠DCE=∠ACD﹣∠ACE=90°﹣60°=30°,
故答案为:30;
(2)∵∠ACB=∠ACD+∠BCE﹣∠DCE=90°+90°﹣∠DCE,
∴∠ACB+∠DCE=180°,
故答案为:∠ACB+∠DCE=180°;
(3)①∵BE∥AC,
∴∠ACE=∠E=45°,
故答案为:45°;
②∵BC∥DA,
∴∠A+∠ACB=180°,
又∵∠A=60°,
∴∠ACB=180°﹣60°=120°,
∵∠BCE=90°,
∴∠BCD=∠ACB﹣∠ECB=120°﹣90°=30°.
3.解:(1)∵CB∥OA,
∴∠AOC=180°﹣∠C=180°﹣112°=68°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=∠AOC=×68°=34°;
(2)∠OBC:∠OFC的值不变.
∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=∠AOC=×68°=17°,
∴∠OEC=180°﹣∠C﹣∠COE=180°﹣112°﹣17°=51°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=51°.
4.解:(1)在△DBC中,∵∠DBC+∠DCB+∠D=180°,
而∠D=90°,
∴∠DBC+∠DCB=90°;
故答案为90;
(2)在△ABC中,
∵∠ABC+∠ACB+∠A=180°,
即∠ABD+∠DBC+∠DCB+∠ACD+∠BAC=180°,
而∠DBC+∠DCB=90°,
∴∠ABD+∠ACD=90°﹣∠BAC,
∴∠ABD+∠BAC=90°﹣∠ACD=70°.
又∵MN∥DE,
∴∠ABD=∠BAN.
而∠BAN+∠BAC+∠CAM=180°,
∴∠ABD+∠BAC+∠CAM=180°,
∴∠CAM=180°﹣(∠ABD+∠BAC)=110°.
5.证明:(1)∵AE⊥CE,
∴∠AEC=90°,
∴∠2+∠3=90°且∠1+∠4=90°,
又∵EC平分∠DEF,
∴∠3=∠4,
∴∠1=∠2,
∴EA平分∠BEF;
(2)∵∠1=∠A,∠4=∠C,
∴∠1+∠A+∠4+∠C=2(∠1+∠4)=180°,
∴∠B+∠D=(180°﹣2∠1)+(180°﹣2∠4)=360°﹣2(∠1+∠4)=180°,
∴AB∥CD.
6.证明:∵DE∥AB(已知),
∴∠A=∠CED(两直线平行,同位角相等)
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD(等量代换)
∴DF∥AE(同位角相等,两直线平行)
∴∠EGF+∠AEG=180°(两直线平行,同旁内角互补)
故答案为:两直线平行,同位角相等;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补.
7.解:(1)过点C作CM∥AE,如答图1所示.
∵CM∥AE,
∴∠EAC=∠ACM.
∵CM∥AE,AE∥BF,
∴CM∥BF,
∴∠FBC=∠BCM.
∵∠ACB=∠ACM+∠BCM=α,∠EAC+∠FBC=β,
∴α=β.
故答案为:α=β.
(2)α=β.理由如下:
过点C作CG∥AM,如答图2所示.
∵CG∥AM,AM∥BN,
∴AM∥BN∥CG,
∴∠MAC=∠ACG,∠NBC=∠BCG,
∵AM是∠EAC的平分线,BN是∠FBC的平分线,
∴∠ACB=∠ACG+∠BCG=∠MAC+∠NBC=∠EAC+∠FBC=(∠EAC+∠FBC)=β.
(3)连接PC并延长到点M,如答图3所示.
∵∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,
∴∠PAC=∠EAC,∠PBC=∠FBC,
∵∠ACM=∠PAC+∠APC,∠BCM=∠PBC+∠BPC,∠ACB=∠ACM+∠BCM,∠APB=∠APC+∠BPC,
∴∠ACB=∠PAC+∠PBC+∠APB,
∵∠ACB=α,∠EAC+∠FBC=β,
∴α=β+∠APB,
∴∠APB=α﹣β.
故答案为:∠APB=α﹣β.
(4)结合(3)结论可知:∠P1=α﹣β,∠P2=α﹣β,∠P3=α﹣β,
∴∠P4=α﹣β,…
∴∠Pn=α﹣β.
故答案为:α﹣β,α﹣β.
8.解:(1)①两直线平行,内错角相等;60;
②30;
③60.
(2)∵AB∥CD,
∴∠B+∠BCE=180°,
∵∠B=40°,
∴∠BCE=180°﹣∠B=180°﹣40°=140°.
又∵CN是∠BCE的平分线,
∴∠BCN=140°÷2=70°.
∵CN⊥CM,
∴∠BCM=90°﹣∠BCN=90°﹣70°=20°.
9.证明:∵∠1=∠3
对顶角相等,
∠1+∠2=180°
已知,
∴∠3+∠2=180°
等量代换,
∴a∥b
同旁内角互补,两直线平行.
故答案为:对顶角相等;已知;等量代换;同旁内角互补,两直线平行.
另一种证法:
∵∠1+∠2=180°,∠1+∠4=180°,
∴∠2=∠4,
∴a∥b.
10.(1)解:如图1,过点I作IM∥AB,
∵EI平分∠AEF,HI平分∠CHG,∠AEF=70°,∠CHG=60°,
∴∠AEI=35°,∠CHI=30°,
∵IM∥AB,
∴∠MIE=∠AEI=35°,
∵AB∥CD,IM∥AB,
∴IM∥CD,
∴∠MIH=∠CHI=30°,
∴∠EIH=∠MIE+∠MIH=35°+30°=65°;
(2)解:如图2,过点I作IM∥AB,
∵EI平分∠AEF,HI平分∠CHG,∠AEF=α,∠CHG=β,
∴∠AEI=,∠CHI=,
∵IM∥AB,
∴∠MIE=∠AEI=,
∵AB∥CD,IM∥AB,
∴IM∥CD,
∴∠MIH=∠CHI=,
∴∠EIH=∠MIE+∠MIH=+;
(3)解:如图3,过点J作MN∥AB,
∵∠AEF=α,
∴∠KEB=α,
∵EJ平分∠KEB,HJ平分∠CHG,∠KEB=α,∠CHG=β,
∴∠JEG=,∠JHF=,
∵MN∥AB,
∴∠MJE=∠JEG=,
∵AB∥CD,MN∥AB,
∴MN∥CD,
∴∠NJH=∠CHJ=,
∴∠EJH=180°﹣∠MJE﹣∠NJH=180°﹣﹣.
11.解:探究:∵DE∥BC,
∴∠DEF=∠EFC.(两直线平行,内错角相等)
∵EF∥AB,
∴∠EFC=∠ABC.(两直线平行,同位角相等)
∴∠DEF=∠ABC.(等量代换)
∵∠ABC=50°,
∴∠DEF=50°.
故答案为:∠EFC,两直线平行,内错角相等,∠EFC,两直线平行,同位角相等,50°;
应用:∵DE∥BC,
∴∠ABC=∠ADE=60°.(两直线平行,同位角相等)
∵EF∥AB,
∴∠ADE+∠DEF=180°.(两直线平行,同旁内角互补)
∴∠DEF=180°﹣65°=115°.
故答案为:115°.
12.解:(1)由平移的性质可得:AA′∥CC′;
故答案为:AA′∥CC′;
(2)根据平移性质可知A'C'∥AC,AA'∥CC',
∴∠A'=∠BAC,∠BAC=∠ACC',
∴∠A'=∠ACC',
∵∠ACC'+∠CAC′+∠AC′C=180°,
∴∠A'+∠CAC'+∠AC'C=180°,
(3)结论:∠CAC'=x+y,
过点A作AD∥BC,交CC'于点D,
根据平移性质可知B'C'∥BC,
∴B'C'∥AD∥BC',
∴∠AC'B'=∠C'AD,∠ACB=∠DAC,
∴∠CAC'=∠C'AD+∠CAD=∠AC'B'+∠ACB=x+y,
即∠CAC'=x+y.
13.证明:(1)∠APB=∠A+∠B这个结论正确,理由如下
如图1,过点P作PQ∥AM,
∵PQ∥AM,AM∥BN,
∴PQ∥AM∥BN,
∴∠A=∠APQ,∠B=∠BPQ,
∴∠A+∠B=∠APQ+∠BPQ=∠APB,
即:∠APB=∠A+∠B.
(2)根据(1)中结论可得,∠A+∠B+∠P2=∠P1+∠P3,
故答案为:∠A+∠B+∠P2=∠P1+∠P3,
(3)由(2)的规律得,∠A+∠B+∠P2+…+P2n=∠P1+∠P3+∠P5+…+∠P2n+1
故答案为:∠A+∠B+∠P2+…+P2n=∠P1+∠P3+∠P5+…+∠P2n+1
14.解:(1)∵|a﹣3|+(a+b﹣4)2=0,
∴a﹣3=0,a+b﹣4=0,
解得:a=3,b=1;
(2)如图1,过点C作CE∥MN,
∵PQ∥MN,
∴CE∥PQ∥MN,
设两灯转动时间为x秒,则∠MAC=3x°,∠PBC=x°,
∴∠CAN=180°﹣3x°,
∴∠BCE=∠PBC=x°,∠ECA=∠CAN=(180﹣3x)°,
∵∠ACB=70°,
∴180﹣3x+x=70,
解得x=55,
∴∠CAN=15°,
∴∠BAC=∠BAN﹣∠CAN=45°﹣15°=30°;
(3)设A灯转动t秒,两灯的光束互相平行,
①在灯A射线到达AN之前,由题意得:3t=(20+t)×1,
解得:t=10;
②在灯A射线到达AN之后,由题意得:3t﹣180=180﹣(20+t)×1,
解得:t=85.
综上所述,A灯转动10秒或85秒时,两灯的光束互相平行.
15.解:(1)如图1,过点P作PM∥AB,
∴∠1=∠AEP=40°.(两直线平行,内错角相等)
∵AB∥CD,(已知)
∴PM∥CD,(平行于同一条直线的两直线平行)
∴∠2+∠PFD=180°.
(两直线平行,同旁内角互补)
∵∠PFD=130°,
∴∠2=180°﹣130°=50°.
∴∠1+∠2=40°+50°=90°.
即∠EPF=90°.
故答案为:两直线平行,内错角相等;平行于同一条直线的两直线平行;两直线平行,同旁内角互补;
(2)∠PFC=∠PEA+∠P.
理由:如图2,过P点作PN∥AB,则PN∥CD,
∴∠PEA=∠NPE,
∵∠FPN=∠NPE+∠FPE,
∴∠FPN=∠PEA+∠FPE,
∵PN∥CD,
∴∠FPN=∠PFC,
∴∠PFC=∠PEA+∠FPE,即∠PFC=∠PEA+∠P;
(3)令AB与PF交点为O,连接EF,如图3.
在△GFE中,∠G=180°﹣(∠GFE+∠GEF),
∵∠GEF=PEA+∠OEF,∠GFE=PFC+∠OFE,
∴∠GEF+∠GFE=PEA+∠OEF+PFC+∠OFE,
∵由(2)知∠PFC=∠PEA+∠P,
∴∠PEA=∠PFC﹣α,
∵∠OFE+∠OEF=180°﹣∠FOE=180°﹣∠PFC,
∴∠GEF+∠GFE=(∠PFC﹣α)+∠PFC+180°﹣∠PFC=180°﹣α,
∴∠G=180°﹣(∠GEF+∠GFE)=180°﹣180°+α=α.
故答案为:α.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
