苏科版七年级数学下册 第7章 平面图形的认识(二)章末易错题专题突破训练(word版含解析)
文档属性
| 名称 | 苏科版七年级数学下册 第7章 平面图形的认识(二)章末易错题专题突破训练(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 239.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-21 17:29:29 | ||
图片预览



文档简介
2020-2021年度苏科版七年级数学下册 第7章平面图形的认识(二)
章末综合易错题专题突破训练(附答案)
1.如图,CD、BD分别平分∠ACE、∠ABC,∠A=80°,则∠BDC=( )
A.35° B.40° C.30° D.45°
2.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,⑤∠7=∠2+∠3,⑥∠7+∠4﹣∠1=180°中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
3.三角形的三边长可以是( )
A.2,11,13 B.5,12,7 C.5,5,11 D.5,12,13
4.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是( )
A.10 B.11 C.12 D.10或11或12
5.如图,将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上,若∠2=44°,则∠1的大小为( )
A.14° B.16° C.24° D.30°
6.如图,AB∥DE,那么∠BCD=( )
A.180°+∠1﹣∠2 B.∠1+∠2
C.∠2﹣∠1 D.180°+∠2﹣2∠1
7.下列命题是真命题的有( )个.
①对顶角相等,邻补角互补;
②两条直线被第三条直线所截,同位角的平分线平行;
③垂直于同一条直线的两条直线互相平行;
④过一点有且只有一条直线与已知直线平行.
A.0 B.1 C.2 D.3
8.如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
①BC平分∠ABE;
②AC∥BE;
③∠CBE+∠D=90°;
④∠DEB=2∠ABC,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.△ABC的三边长分别为1,3,x,且x为整数,则x的值是 .
10.一个正五边形和一个正六边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠1+∠2= °.
11.如图,已知点D,F分别在∠BAC边AB和AC上,点E在∠BAC的内部,DF平分∠ADE.若∠BAC=∠BDE=70°,则∠AFD的度数为 .
12.已知在△ABC中,∠A=30°,BD是△ABC的高,∠BCD=80°,则∠ACB= °.
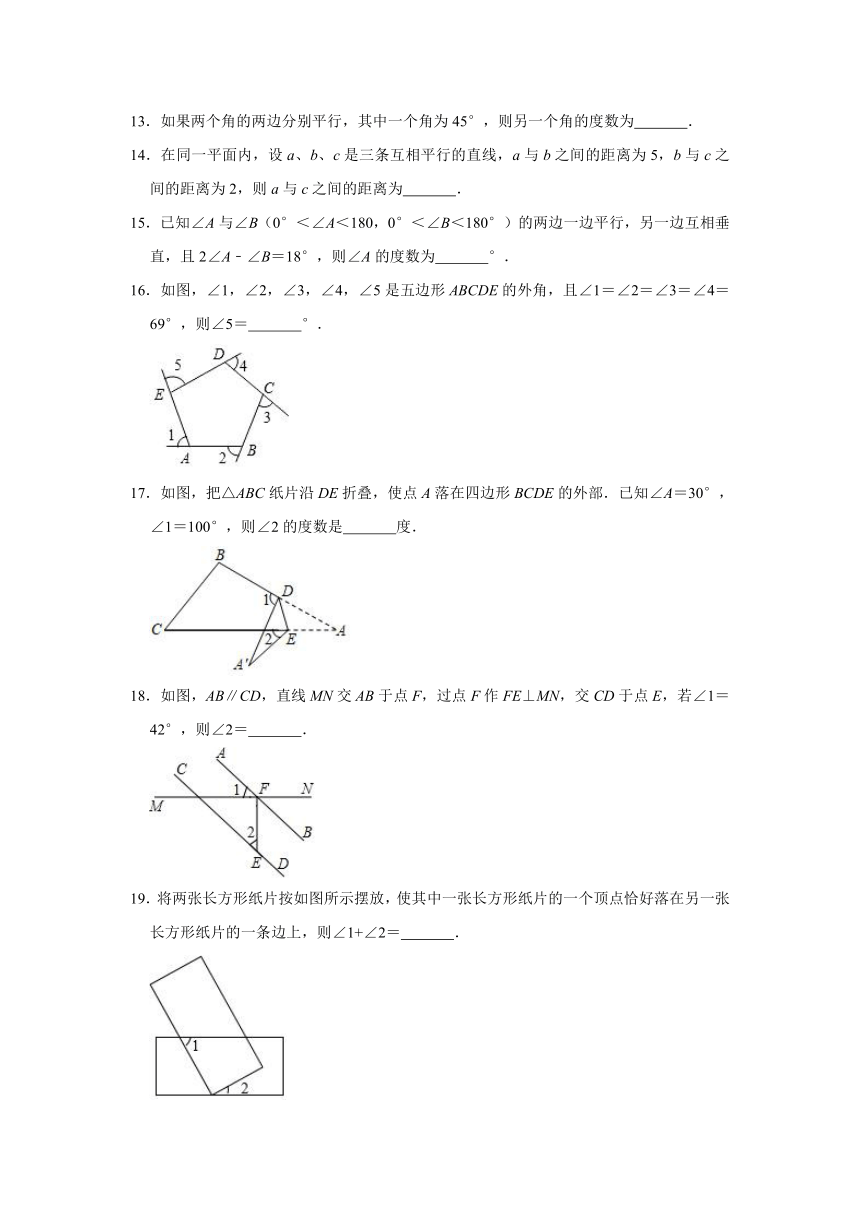
13.如果两个角的两边分别平行,其中一个角为45°,则另一个角的度数为 .
14.在同一平面内,设a、b、c是三条互相平行的直线,a与b之间的距离为5,b与c之间的距离为2,则a与c之间的距离为 .
15.已知∠A与∠B(0°<∠A<180,0°<∠B<180°)的两边一边平行,另一边互相垂直,且2∠A﹣∠B=18°,则∠A的度数为 °.
16.如图,∠1,∠2,∠3,∠4,∠5是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=69°,则∠5= °.
17.如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的外部.已知∠A=30°,∠1=100°,则∠2的度数是 度.
18.如图,AB∥CD,直线MN交AB于点F,过点F作FE⊥MN,交CD于点E,若∠1=42°,则∠2= .
19.将两张长方形纸片按如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则∠1+∠2= .
20.如图,AM、CM平分∠BAD和∠BCD,若∠B=34°,∠D=42°,则∠M= .
21.如图所示
(1)独立思考:
①图中的对顶角有 对;
②图中互补的角有 (写出2对即可);
③写出图中的同位角2对 , ,内错角2对 , ;
(2)合作探究:如果∠1=∠2,∠B=∠C,你能判断哪两条直线平行,写出来,并说明平行理由.
22.已知一个正多边形相邻的内角比外角大140°.
(1)求这个正多边形的内角与外角的度数;
(2)直接写出这个正多边形的边数;
(3)只用这个正多边形若干个,能否镶嵌?并说明理由.
23.如图,已知AB∥CD,∠1=∠2,∠3=∠4,请说明AD∥BC.
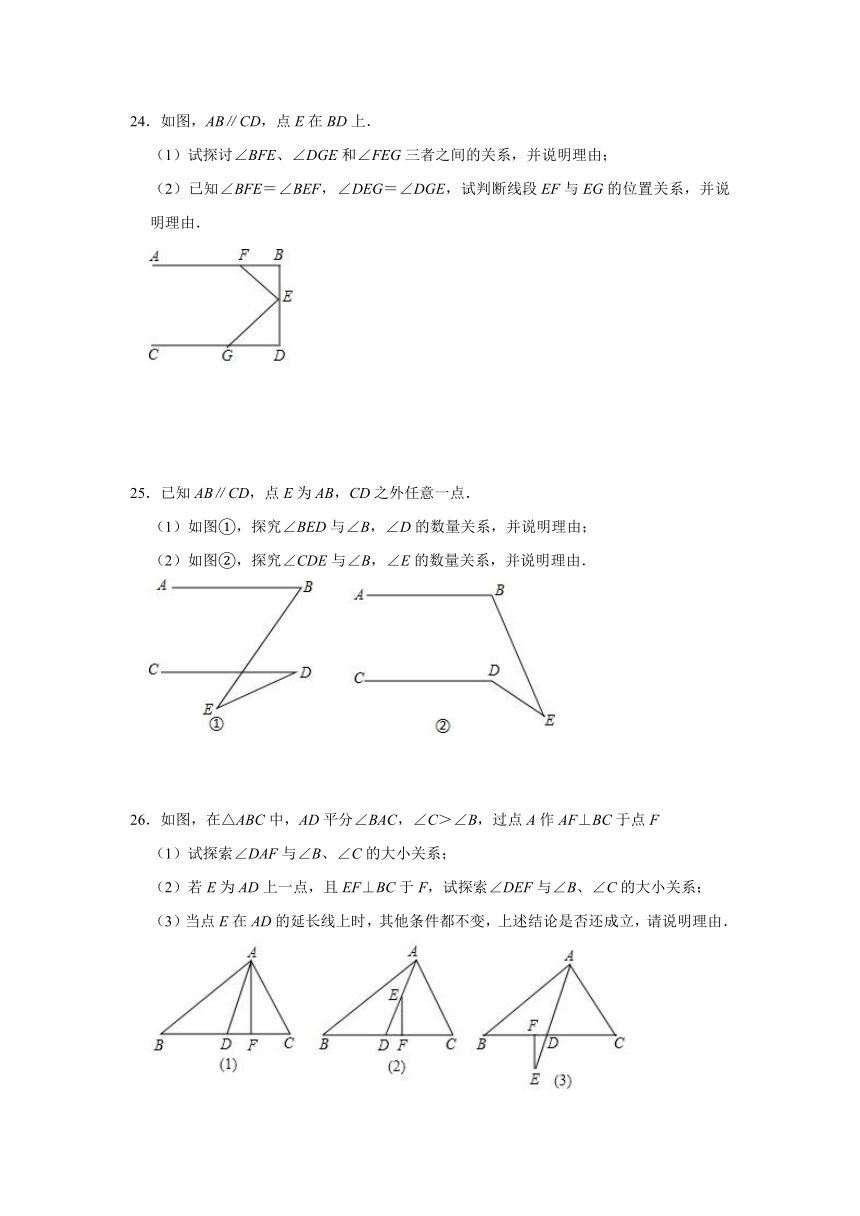
24.如图,AB∥CD,点E在BD上.
(1)试探讨∠BFE、∠DGE和∠FEG三者之间的关系,并说明理由;
(2)已知∠BFE=∠BEF,∠DEG=∠DGE,试判断线段EF与EG的位置关系,并说明理由.
25.已知AB∥CD,点E为AB,CD之外任意一点.
(1)如图①,探究∠BED与∠B,∠D的数量关系,并说明理由;
(2)如图②,探究∠CDE与∠B,∠E的数量关系,并说明理由.
26.如图,在△ABC中,AD平分∠BAC,∠C>∠B,过点A作AF⊥BC于点F
(1)试探索∠DAF与∠B、∠C的大小关系;
(2)若E为AD上一点,且EF⊥BC于F,试探索∠DEF与∠B、∠C的大小关系;
(3)当点E在AD的延长线上时,其他条件都不变,上述结论是否还成立,请说明理由.
27.如图,在△ABC中,∠BAC=50°.
(1)若点I是∠ABC,∠ACB的角平分线的交点,则∠BIC= °.
(2)若点D是∠ABC,∠ACB的外角平分线的交点,则∠BDC= °.
(3)若点E是∠ABC,∠ACG的平分线的交点,探索∠BEC与∠BAC的数量关系,并说明理由.
(4)在(3)的条件下,若CE∥AB,求∠ACB的度数.
参考答案
1.解:∵∠ACE是△ABC的外角,
∴∠A=∠ACE﹣∠ABC,
∵CD、BD分别平分∠ACE、∠ABC,
∴∠DCE=∠ACE,∠DBE=∠ABC,
∵∠DCE是△BCD的外角,
∴∠D=∠DCE﹣∠DBC=∠ACE﹣∠ABC=(∠ACE﹣∠ABC)===40°,
故选:B.
2.解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠2=∠3,不能得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠7+∠4﹣∠1=180°,∠7﹣∠1=∠3,可得∠3+∠4=180°,即可得到a∥b;
故选:C.
3.解:A.2,11,13中,2+11=13,不合题意;
B.5,12,7中,5+7=12,不合题意;
C.5,5,11中,5+5<11,不合题意;
D.5,12,13中,5+12>13,能组成三角形;
故选:D.
4.解:设多边形截去一个角的边数为n,
则(n﹣2)?180°=1620°,
解得n=11,
∵截去一个角后边上可以增加1,不变,减少1,
∴原来多边形的边数是10或11或12.
故选:D.
5.解:如图:
∵矩形的对边平行,
∴∠2=∠3=44°,
根据三角形外角性质,可得∠3=∠1+30°,
∴∠1=44°﹣30°=14°,
故选:A.
6.解:过点C作CF∥AB,如图:
∵AB∥DE,
∴AB∥DE∥CF,
∴∠BCF=∠1①,∠2+∠DCF=180°②,
∴①+②得,∠BCF+∠DCF+∠2=∠1+180°,即∠BCD=180°+∠1﹣∠2.
故选:A.
7.解:①对顶角相等,邻补角互补,原说法正确,故①是真命题;
②两条平行线被第三条直线所截,同位角的平分线平行,原说法错误,故②是假命题
③在同一平面内,垂直于同一条直线的两条直线互相平行,原说法错误,故③是假命题;
④过直线外一点有且只有一条直线与已知直线平行,原说法错误,故④是假命题;
所以真命题的有1个.
故选:B.
8.解:∵AF∥CD,
∴∠ABC=∠ECB,∠EDB=∠DBF,∠DEB=∠EBA,
∵CB平分∠ACD,BD平分∠EBF,
∴∠ECB=∠BCA,∠EBD=∠DBF,
∴∠EDB=∠DBE,
∵BC⊥BD,
∴∠EDB+∠ECB=90°,∠DBE+∠EBC=90°,
∴∠ECB=∠EBC,
∴∠ECB=∠EBC=∠ABC=∠BCA,
∴BC平分∠ABE,①正确;
∵∠EBC=∠BCA,
∴AC∥BE,②正确;
∴∠CBE+∠EDB=90°,③正确;
∵∠DEB=∠EBA=2∠ABC,故④正确;
故选:D.
9.解:根据三角形三边关系,
∴三角形的第三边x满足:3﹣1<x<3+1,即2<x<4,
∵x为整数,
∴x=3,
故答案为:3.
10.解:如图:
由题意:∠AOE=108°,∠BOF=120°,∠OEF=72°,∠OFE=60°,
∴∠2=180°﹣72°﹣60°=48°,
∴∠1=360°﹣108°﹣48°﹣120°=84°,
∴∠1+∠2=84°+48°=132°,
故答案为:132.
11.解:因为∠BAC=∠BDE,
所以DE∥AC,
所以∠BAC+∠ADE=180°,
因为∠BAC=70°,
所以∠ADE=180°﹣∠BAC=180°﹣70°=110°,
因为DF平分∠ADE,
所以∠AFD=∠ADE=×110°=55°.
故答案为:55°.
12.解:(1)如图,当△ABC为锐角三角形时,
∠ACB=∠BCD=80°,
(2)如图,当△ABC为钝角三角形时,
∠ACB=180°﹣∠BCD=100°.
故答案为:80°或100.
13.解:其中一个角为45°,
若两角相等,则另一个角的度数为45°;
若两角互补,则另一个角的度数为180°﹣45°=135°;
故答案为:45°或135°.
14.解:有两种情况:
①如图①所示,直线a与c之间的距离是5+2=7;
②如图②所示,直线a与c之间的距离是5﹣2=3;
综上所述,a与c之间的距离为7或3.
故答案为:7或3.
15.解:若∠DAC是锐角时,过点C
作FC∥AD,如图1所示:
∵AC⊥BC,
∴∠ACB=90°,
又∵∠1+∠2=∠ACB,
∴∠1+∠2=90°,
又∵FC∥AD,
∴∠A=∠1,
又∵AD∥BE,
∴FC∥BE,
∴∠2=∠B,
∴∠A+∠B=90°,
又∵2∠A﹣∠B=18°,
∴∠A=36°;
若∠DAC是钝角时.过点C
作FC∥AD,如图2所示:
同理可得:∠1+∠2=90°,
∵CF∥AD,
∴∠A+∠1=180°,
又∵AD∥BE,
∴CF∥BE,
∴∠2+∠B=180°,
∴∠1+∠2+∠A+∠B=360°,
∴∠A+∠B=270°,
又∵2∠A﹣∠B=18°,
∴∠A=96°;
综合所述:∠A的度数为36°或96°,
故答案为36或96.
16.解:∵∠1=∠2=∠3=∠4=69°,
∴∠5=360°﹣69°×4=360°﹣276°=84°.
故答案为:84.
17.解:如图
∵∠1=100°,
∴∠ADF=80°,
∵△A′ED是△AED翻折变换而成,
∴∠A′=∠A=30°,
∵∠A′FE是△ADF的外角,
∴∠A′FE=∠A+∠ADF=30°+80°=110°,
∵∠A′FE+∠2+∠A′=180°,
∴110°+∠2+30°=180°,
∴∠2=40°.
故答案为:40.
18.解:如图:
∵AB∥CD,
∴∠3=∠1=42°.
又∵FE⊥MN,
∴∠MFE=90°,
∴∠2=90°﹣∠3=48°.
故答案为:48°.
19.解:∵AE∥BD,
∴∠1=∠3,
又∵∠ABC=90°,
∴∠3+∠2=180°﹣90°=90°,
∴∠1+∠2=90°,
故答案为:90°.
20.解:∵∠B+∠BAM=∠M+∠BCM,
∴∠BAM﹣∠BCM=∠M﹣∠B,
同理,∠MAD﹣∠MCD=∠D﹣∠M,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠BAM=∠MAD,∠BCM=∠MCD,
∴∠M﹣∠B=∠D﹣∠M,
∴∠M=(∠B+∠D)=(34°+42°)=38°.
故答案为38°.
21.解:(1)①图中的对顶角有4对:∠1和∠CGD,∠AGC和∠EGD,∠AMB和∠FMD,∠AMF和∠BMD;
②互补的角有:∠1和∠EGD,∠2和∠BFC;
③同位角:∠1和∠AMB,∠2和∠C,
内错角:∠EGD和∠AMF,∠CGD和∠AMB;
(2)如果∠1=∠2,∠B=∠C,不能判断图中的直线平行,因为不具备平行的条件.
22.解:(1)设正多边形的外角为x°,则内角为(180﹣x)°,
∴180﹣x﹣x=140,
解得x=20,
∴正多边形的内角为160°,外角为20°;
(2)这个正多边形的边数为:360°÷20°=18.
(3)正多边形的内角为160°,不能整除360°,不能镶嵌.
23.证明:∵AB∥CD(已知),
∴∠4=∠BAE(两直线平行,同位角相等),
∵∠3=∠4(已知)
∴∠3=∠BAE(等量代换),
∵∠1=∠2(已知),
∴∠CAE+∠1=∠CAE+∠2,即∠BAE=∠DAC,
∴∠3=∠DAC,
∴AD∥BC(内错角相等,两直线平行).
24.解:过点E作EF∥AB,如图所示:
(1)∠FEG=∠BFE+∠DGE,理由如下:
∵AB∥CD,
∴∠BFE=∠1,
又∵EF∥AB,
∴EF∥CD,
∴∠2=∠DGE,
又∵∠FEG=∠1+∠2,
∴∠FEG=∠BFE+∠DGE;
(2)EF⊥EG,理由如下:
∵∠BFE=∠BEF,∠DEG=∠DGE,
∴∠1=∠BEF,∠2=∠DEG,
又∵∠1+∠2+∠BEF+∠DEG=180°,
∴∠1+∠2=90°,
∴EF⊥EG.
25.解:(1)如图①,设CD、BE交于点F,
∵AB∥CD,
∴∠B=∠BFD,
又∠BFD=∠BED+∠D,
∴∠B=∠BED+∠D;
(2)如图②,延长CD交BE于点F,
∵AB∥CD,
∴∠B=∠DFE,
又∠CDE=∠DFE+∠BED,
∴∠CDE=∠B+∠BED.
26.解:(1)如图1,∵AD平分∠BAC,
∴∠CAD=∠BAC,
∵AF⊥BC,
∴∠CAF=90°﹣∠C,
∴∠DAF=∠CAD﹣∠CAF=∠BAC﹣(90°﹣∠C)
=(180°﹣∠B﹣∠C)﹣(90°﹣∠C)
=∠C﹣∠B=(∠C﹣∠B);
(2)如图2,过A作AG⊥BC于G,
∵EF⊥BC,
∴AG∥EF,
∴∠DAG=∠DEF,
由(1)可得,∠DAG=(∠C﹣∠B),
∴∠DEF=(∠C﹣∠B);
(3)仍成立.
如图3,过A作AG⊥BC于G,
∵EF⊥BC,
∴AG∥EF,
∴∠DAG=∠DEF,
由(1)可得,∠DAG=(∠C﹣∠B),
∴∠DEF=(∠C﹣∠B).
27.解:(1)∵△ABC中,∠BAC=50°,
∴∠ABC+∠ACB=130°,
∵点I是∠ABC,∠ACB的角平分线的交点,
∴∠IBC+∠ICB=65°,
∴△IBC中,∠BIC=180°﹣65°=115°;
(2)∵△ABC中,∠BAC=50°,
∴∠ABC+∠ACB=130°,
∴∠ABC,∠ACB的外角之和=360°﹣130°=230°,
∵点D是∠ABC,∠ACB的外角平分线的交点,
∴∠DBC+∠DCB=115°,
∴△DBC中,∠BDC=180°﹣115°=65°;
(3)∠BEC=∠BAC.
∵∠DCE是△BCE的外角,
∴∠E=∠DCE﹣∠CBE,
∵点E是∠ABC,∠ACG的平分线的交点,
∴∠DCE=∠ACD,∠CBE=∠ABC,
∴∠E=∠ACD﹣∠ABC=(∠ACD﹣∠ABC)=∠A,
即∠BEC=∠BAC;
(4)∵CE∥AB,
∴∠A=∠ACE=50°,
∵CE平分∠ACD,
∴∠ACD=100°,
∴∠ACB=180°﹣100=80°.
章末综合易错题专题突破训练(附答案)
1.如图,CD、BD分别平分∠ACE、∠ABC,∠A=80°,则∠BDC=( )
A.35° B.40° C.30° D.45°
2.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,⑤∠7=∠2+∠3,⑥∠7+∠4﹣∠1=180°中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
3.三角形的三边长可以是( )
A.2,11,13 B.5,12,7 C.5,5,11 D.5,12,13
4.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是( )
A.10 B.11 C.12 D.10或11或12
5.如图,将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上,若∠2=44°,则∠1的大小为( )
A.14° B.16° C.24° D.30°
6.如图,AB∥DE,那么∠BCD=( )
A.180°+∠1﹣∠2 B.∠1+∠2
C.∠2﹣∠1 D.180°+∠2﹣2∠1
7.下列命题是真命题的有( )个.
①对顶角相等,邻补角互补;
②两条直线被第三条直线所截,同位角的平分线平行;
③垂直于同一条直线的两条直线互相平行;
④过一点有且只有一条直线与已知直线平行.
A.0 B.1 C.2 D.3
8.如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
①BC平分∠ABE;
②AC∥BE;
③∠CBE+∠D=90°;
④∠DEB=2∠ABC,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.△ABC的三边长分别为1,3,x,且x为整数,则x的值是 .
10.一个正五边形和一个正六边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠1+∠2= °.
11.如图,已知点D,F分别在∠BAC边AB和AC上,点E在∠BAC的内部,DF平分∠ADE.若∠BAC=∠BDE=70°,则∠AFD的度数为 .
12.已知在△ABC中,∠A=30°,BD是△ABC的高,∠BCD=80°,则∠ACB= °.
13.如果两个角的两边分别平行,其中一个角为45°,则另一个角的度数为 .
14.在同一平面内,设a、b、c是三条互相平行的直线,a与b之间的距离为5,b与c之间的距离为2,则a与c之间的距离为 .
15.已知∠A与∠B(0°<∠A<180,0°<∠B<180°)的两边一边平行,另一边互相垂直,且2∠A﹣∠B=18°,则∠A的度数为 °.
16.如图,∠1,∠2,∠3,∠4,∠5是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=69°,则∠5= °.
17.如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的外部.已知∠A=30°,∠1=100°,则∠2的度数是 度.
18.如图,AB∥CD,直线MN交AB于点F,过点F作FE⊥MN,交CD于点E,若∠1=42°,则∠2= .
19.将两张长方形纸片按如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则∠1+∠2= .
20.如图,AM、CM平分∠BAD和∠BCD,若∠B=34°,∠D=42°,则∠M= .
21.如图所示
(1)独立思考:
①图中的对顶角有 对;
②图中互补的角有 (写出2对即可);
③写出图中的同位角2对 , ,内错角2对 , ;
(2)合作探究:如果∠1=∠2,∠B=∠C,你能判断哪两条直线平行,写出来,并说明平行理由.
22.已知一个正多边形相邻的内角比外角大140°.
(1)求这个正多边形的内角与外角的度数;
(2)直接写出这个正多边形的边数;
(3)只用这个正多边形若干个,能否镶嵌?并说明理由.
23.如图,已知AB∥CD,∠1=∠2,∠3=∠4,请说明AD∥BC.
24.如图,AB∥CD,点E在BD上.
(1)试探讨∠BFE、∠DGE和∠FEG三者之间的关系,并说明理由;
(2)已知∠BFE=∠BEF,∠DEG=∠DGE,试判断线段EF与EG的位置关系,并说明理由.
25.已知AB∥CD,点E为AB,CD之外任意一点.
(1)如图①,探究∠BED与∠B,∠D的数量关系,并说明理由;
(2)如图②,探究∠CDE与∠B,∠E的数量关系,并说明理由.
26.如图,在△ABC中,AD平分∠BAC,∠C>∠B,过点A作AF⊥BC于点F
(1)试探索∠DAF与∠B、∠C的大小关系;
(2)若E为AD上一点,且EF⊥BC于F,试探索∠DEF与∠B、∠C的大小关系;
(3)当点E在AD的延长线上时,其他条件都不变,上述结论是否还成立,请说明理由.
27.如图,在△ABC中,∠BAC=50°.
(1)若点I是∠ABC,∠ACB的角平分线的交点,则∠BIC= °.
(2)若点D是∠ABC,∠ACB的外角平分线的交点,则∠BDC= °.
(3)若点E是∠ABC,∠ACG的平分线的交点,探索∠BEC与∠BAC的数量关系,并说明理由.
(4)在(3)的条件下,若CE∥AB,求∠ACB的度数.
参考答案
1.解:∵∠ACE是△ABC的外角,
∴∠A=∠ACE﹣∠ABC,
∵CD、BD分别平分∠ACE、∠ABC,
∴∠DCE=∠ACE,∠DBE=∠ABC,
∵∠DCE是△BCD的外角,
∴∠D=∠DCE﹣∠DBC=∠ACE﹣∠ABC=(∠ACE﹣∠ABC)===40°,
故选:B.
2.解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠2=∠3,不能得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠7+∠4﹣∠1=180°,∠7﹣∠1=∠3,可得∠3+∠4=180°,即可得到a∥b;
故选:C.
3.解:A.2,11,13中,2+11=13,不合题意;
B.5,12,7中,5+7=12,不合题意;
C.5,5,11中,5+5<11,不合题意;
D.5,12,13中,5+12>13,能组成三角形;
故选:D.
4.解:设多边形截去一个角的边数为n,
则(n﹣2)?180°=1620°,
解得n=11,
∵截去一个角后边上可以增加1,不变,减少1,
∴原来多边形的边数是10或11或12.
故选:D.
5.解:如图:
∵矩形的对边平行,
∴∠2=∠3=44°,
根据三角形外角性质,可得∠3=∠1+30°,
∴∠1=44°﹣30°=14°,
故选:A.
6.解:过点C作CF∥AB,如图:
∵AB∥DE,
∴AB∥DE∥CF,
∴∠BCF=∠1①,∠2+∠DCF=180°②,
∴①+②得,∠BCF+∠DCF+∠2=∠1+180°,即∠BCD=180°+∠1﹣∠2.
故选:A.
7.解:①对顶角相等,邻补角互补,原说法正确,故①是真命题;
②两条平行线被第三条直线所截,同位角的平分线平行,原说法错误,故②是假命题
③在同一平面内,垂直于同一条直线的两条直线互相平行,原说法错误,故③是假命题;
④过直线外一点有且只有一条直线与已知直线平行,原说法错误,故④是假命题;
所以真命题的有1个.
故选:B.
8.解:∵AF∥CD,
∴∠ABC=∠ECB,∠EDB=∠DBF,∠DEB=∠EBA,
∵CB平分∠ACD,BD平分∠EBF,
∴∠ECB=∠BCA,∠EBD=∠DBF,
∴∠EDB=∠DBE,
∵BC⊥BD,
∴∠EDB+∠ECB=90°,∠DBE+∠EBC=90°,
∴∠ECB=∠EBC,
∴∠ECB=∠EBC=∠ABC=∠BCA,
∴BC平分∠ABE,①正确;
∵∠EBC=∠BCA,
∴AC∥BE,②正确;
∴∠CBE+∠EDB=90°,③正确;
∵∠DEB=∠EBA=2∠ABC,故④正确;
故选:D.
9.解:根据三角形三边关系,
∴三角形的第三边x满足:3﹣1<x<3+1,即2<x<4,
∵x为整数,
∴x=3,
故答案为:3.
10.解:如图:
由题意:∠AOE=108°,∠BOF=120°,∠OEF=72°,∠OFE=60°,
∴∠2=180°﹣72°﹣60°=48°,
∴∠1=360°﹣108°﹣48°﹣120°=84°,
∴∠1+∠2=84°+48°=132°,
故答案为:132.
11.解:因为∠BAC=∠BDE,
所以DE∥AC,
所以∠BAC+∠ADE=180°,
因为∠BAC=70°,
所以∠ADE=180°﹣∠BAC=180°﹣70°=110°,
因为DF平分∠ADE,
所以∠AFD=∠ADE=×110°=55°.
故答案为:55°.
12.解:(1)如图,当△ABC为锐角三角形时,
∠ACB=∠BCD=80°,
(2)如图,当△ABC为钝角三角形时,
∠ACB=180°﹣∠BCD=100°.
故答案为:80°或100.
13.解:其中一个角为45°,
若两角相等,则另一个角的度数为45°;
若两角互补,则另一个角的度数为180°﹣45°=135°;
故答案为:45°或135°.
14.解:有两种情况:
①如图①所示,直线a与c之间的距离是5+2=7;
②如图②所示,直线a与c之间的距离是5﹣2=3;
综上所述,a与c之间的距离为7或3.
故答案为:7或3.
15.解:若∠DAC是锐角时,过点C
作FC∥AD,如图1所示:
∵AC⊥BC,
∴∠ACB=90°,
又∵∠1+∠2=∠ACB,
∴∠1+∠2=90°,
又∵FC∥AD,
∴∠A=∠1,
又∵AD∥BE,
∴FC∥BE,
∴∠2=∠B,
∴∠A+∠B=90°,
又∵2∠A﹣∠B=18°,
∴∠A=36°;
若∠DAC是钝角时.过点C
作FC∥AD,如图2所示:
同理可得:∠1+∠2=90°,
∵CF∥AD,
∴∠A+∠1=180°,
又∵AD∥BE,
∴CF∥BE,
∴∠2+∠B=180°,
∴∠1+∠2+∠A+∠B=360°,
∴∠A+∠B=270°,
又∵2∠A﹣∠B=18°,
∴∠A=96°;
综合所述:∠A的度数为36°或96°,
故答案为36或96.
16.解:∵∠1=∠2=∠3=∠4=69°,
∴∠5=360°﹣69°×4=360°﹣276°=84°.
故答案为:84.
17.解:如图
∵∠1=100°,
∴∠ADF=80°,
∵△A′ED是△AED翻折变换而成,
∴∠A′=∠A=30°,
∵∠A′FE是△ADF的外角,
∴∠A′FE=∠A+∠ADF=30°+80°=110°,
∵∠A′FE+∠2+∠A′=180°,
∴110°+∠2+30°=180°,
∴∠2=40°.
故答案为:40.
18.解:如图:
∵AB∥CD,
∴∠3=∠1=42°.
又∵FE⊥MN,
∴∠MFE=90°,
∴∠2=90°﹣∠3=48°.
故答案为:48°.
19.解:∵AE∥BD,
∴∠1=∠3,
又∵∠ABC=90°,
∴∠3+∠2=180°﹣90°=90°,
∴∠1+∠2=90°,
故答案为:90°.
20.解:∵∠B+∠BAM=∠M+∠BCM,
∴∠BAM﹣∠BCM=∠M﹣∠B,
同理,∠MAD﹣∠MCD=∠D﹣∠M,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠BAM=∠MAD,∠BCM=∠MCD,
∴∠M﹣∠B=∠D﹣∠M,
∴∠M=(∠B+∠D)=(34°+42°)=38°.
故答案为38°.
21.解:(1)①图中的对顶角有4对:∠1和∠CGD,∠AGC和∠EGD,∠AMB和∠FMD,∠AMF和∠BMD;
②互补的角有:∠1和∠EGD,∠2和∠BFC;
③同位角:∠1和∠AMB,∠2和∠C,
内错角:∠EGD和∠AMF,∠CGD和∠AMB;
(2)如果∠1=∠2,∠B=∠C,不能判断图中的直线平行,因为不具备平行的条件.
22.解:(1)设正多边形的外角为x°,则内角为(180﹣x)°,
∴180﹣x﹣x=140,
解得x=20,
∴正多边形的内角为160°,外角为20°;
(2)这个正多边形的边数为:360°÷20°=18.
(3)正多边形的内角为160°,不能整除360°,不能镶嵌.
23.证明:∵AB∥CD(已知),
∴∠4=∠BAE(两直线平行,同位角相等),
∵∠3=∠4(已知)
∴∠3=∠BAE(等量代换),
∵∠1=∠2(已知),
∴∠CAE+∠1=∠CAE+∠2,即∠BAE=∠DAC,
∴∠3=∠DAC,
∴AD∥BC(内错角相等,两直线平行).
24.解:过点E作EF∥AB,如图所示:
(1)∠FEG=∠BFE+∠DGE,理由如下:
∵AB∥CD,
∴∠BFE=∠1,
又∵EF∥AB,
∴EF∥CD,
∴∠2=∠DGE,
又∵∠FEG=∠1+∠2,
∴∠FEG=∠BFE+∠DGE;
(2)EF⊥EG,理由如下:
∵∠BFE=∠BEF,∠DEG=∠DGE,
∴∠1=∠BEF,∠2=∠DEG,
又∵∠1+∠2+∠BEF+∠DEG=180°,
∴∠1+∠2=90°,
∴EF⊥EG.
25.解:(1)如图①,设CD、BE交于点F,
∵AB∥CD,
∴∠B=∠BFD,
又∠BFD=∠BED+∠D,
∴∠B=∠BED+∠D;
(2)如图②,延长CD交BE于点F,
∵AB∥CD,
∴∠B=∠DFE,
又∠CDE=∠DFE+∠BED,
∴∠CDE=∠B+∠BED.
26.解:(1)如图1,∵AD平分∠BAC,
∴∠CAD=∠BAC,
∵AF⊥BC,
∴∠CAF=90°﹣∠C,
∴∠DAF=∠CAD﹣∠CAF=∠BAC﹣(90°﹣∠C)
=(180°﹣∠B﹣∠C)﹣(90°﹣∠C)
=∠C﹣∠B=(∠C﹣∠B);
(2)如图2,过A作AG⊥BC于G,
∵EF⊥BC,
∴AG∥EF,
∴∠DAG=∠DEF,
由(1)可得,∠DAG=(∠C﹣∠B),
∴∠DEF=(∠C﹣∠B);
(3)仍成立.
如图3,过A作AG⊥BC于G,
∵EF⊥BC,
∴AG∥EF,
∴∠DAG=∠DEF,
由(1)可得,∠DAG=(∠C﹣∠B),
∴∠DEF=(∠C﹣∠B).
27.解:(1)∵△ABC中,∠BAC=50°,
∴∠ABC+∠ACB=130°,
∵点I是∠ABC,∠ACB的角平分线的交点,
∴∠IBC+∠ICB=65°,
∴△IBC中,∠BIC=180°﹣65°=115°;
(2)∵△ABC中,∠BAC=50°,
∴∠ABC+∠ACB=130°,
∴∠ABC,∠ACB的外角之和=360°﹣130°=230°,
∵点D是∠ABC,∠ACB的外角平分线的交点,
∴∠DBC+∠DCB=115°,
∴△DBC中,∠BDC=180°﹣115°=65°;
(3)∠BEC=∠BAC.
∵∠DCE是△BCE的外角,
∴∠E=∠DCE﹣∠CBE,
∵点E是∠ABC,∠ACG的平分线的交点,
∴∠DCE=∠ACD,∠CBE=∠ABC,
∴∠E=∠ACD﹣∠ABC=(∠ACD﹣∠ABC)=∠A,
即∠BEC=∠BAC;
(4)∵CE∥AB,
∴∠A=∠ACE=50°,
∵CE平分∠ACD,
∴∠ACD=100°,
∴∠ACB=180°﹣100=80°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
