2020-2021学年九年级下册数学沪教新版《第27章 圆与正多边形-第1节 圆的基本性质》同步测试卷(word有答案)
文档属性
| 名称 | 2020-2021学年九年级下册数学沪教新版《第27章 圆与正多边形-第1节 圆的基本性质》同步测试卷(word有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 290.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 00:00:00 | ||
图片预览





文档简介
2020-2021学年九年级下册数学沪教新版《第27章
圆与正多边形-第1节
圆的基本性质》单元测试卷
一.选择题
1.在⊙O中,=2,那么
.
A.AB=2CD
B.AB=CD
C.AB<2DC
D.AB>2DC.
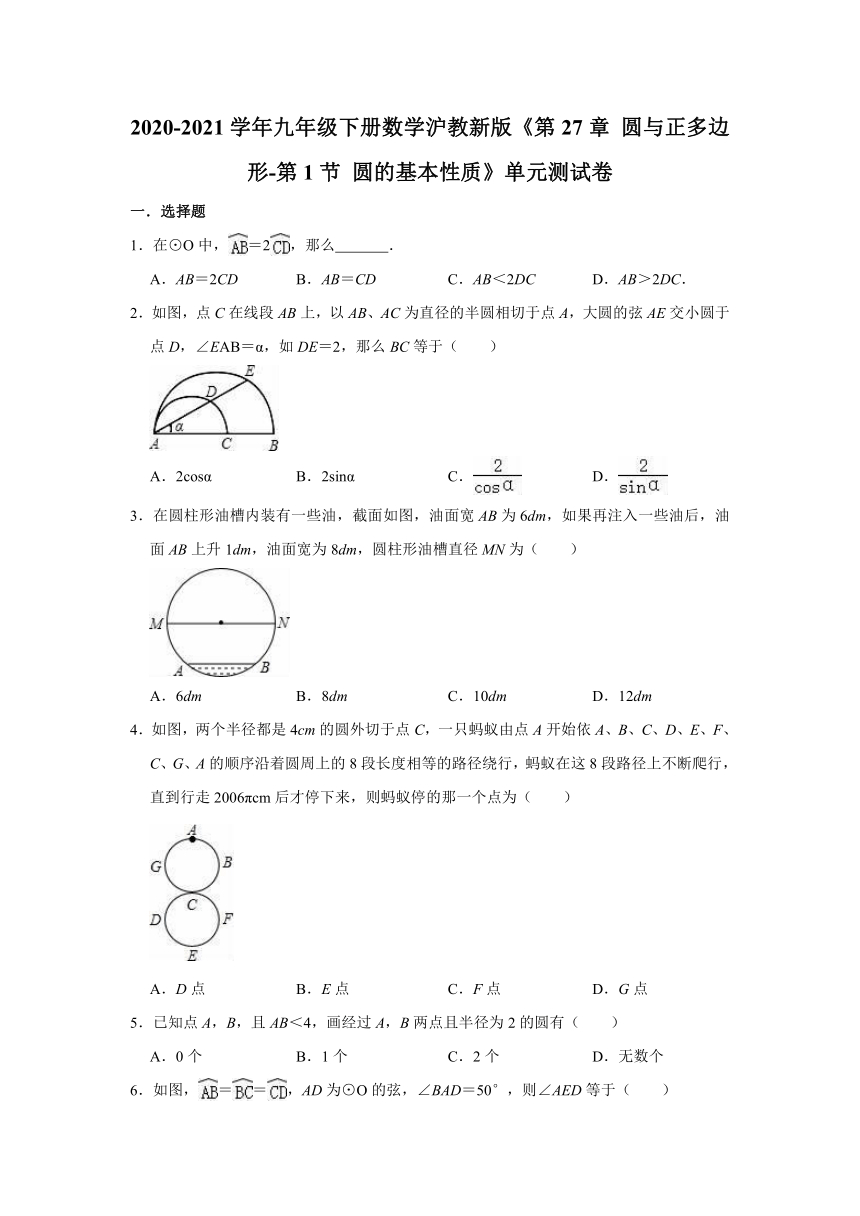
2.如图,点C在线段AB上,以AB、AC为直径的半圆相切于点A,大圆的弦AE交小圆于点D,∠EAB=α,如DE=2,那么BC等于( )
A.2cosα
B.2sinα
C.
D.
3.在圆柱形油槽内装有一些油,截面如图,油面宽AB为6dm,如果再注入一些油后,油面AB上升1dm,油面宽为8dm,圆柱形油槽直径MN为( )
A.6dm
B.8dm
C.10dm
D.12dm
4.如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
A.D点
B.E点
C.F点
D.G点
5.已知点A,B,且AB<4,画经过A,B两点且半径为2的圆有( )
A.0个
B.1个
C.2个
D.无数个
6.如图,==,AD为⊙O的弦,∠BAD=50°,则∠AED等于( )
A.50°
B.60°
C.70°
D.75°
7.在平行四边形、矩形、正方形、菱形、等腰梯形、直角梯形中,必定存在外接圆的有( )
A.1个
B.2个
C.3个
D.4个
8.在Rt△ABC,AB=AC=2,∠BAC=90°,能完全覆盖住此三角形的最小圆的面积是( )
A.π
B.2π
C.3π
D.4π
9.已知⊙O半径为5,OP=8,点Q在⊙O上运动,设PQ的最大值为m,最小值为n,则m﹣n的值为( )
A.5
B.10
C.12
D.8
二.填空题
10.如图,△ABC是⊙O的内接三角形,BC=4cm,∠A=30°,则△OBC的面积为
cm2.
11.已知直线l:y=x﹣4,点A(0,2),点B(2,0),设点P为直线l上一动点,当P的坐标为
时,过P,A,B三点不能作出一个圆.
12.如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠D=
.
13.在同圆或等圆中,同弧或等弧所对圆周角
,相等的圆周角所对的弧
,同弧或等弧所对圆周角是其所对的圆心角的
.
14.在矩形ABCD中,AB=8,AD=6,以A为圆心作圆,如果B,C,D三点中至少有一点在圆内,且至少有一点在圆外,则圆A的半径r的取值范围是
.
15.如图,水平放着的圆柱形排水管的截面为1000mm,其中水面宽AB=800mm,则水的最大深度为
mm.
16.如图,⊙O中弦AB⊥AC,D,E分别是AB,AC的中点.
(1)若AB=AC,则四边形OEAD是
形;
(2)若OD=3,半径r=5,则AB=
cm,AC=
cm.
17.如图,△ABC内接于⊙O,∠C=30°,AB=4,连接OA,OB,则扇形OAB的面积为
.
18.如右图中有
条直径,有
条弦,以点A为端点的优弧有
条,有劣弧
条.
三.解答题
19.如图是一个圆环,外圆半径R=20
cm,内圆半径r=10
cm,求这个圆环的面积.
20.如图已知A、B两点,
求作(1)经过A、B两点的圆⊙O;(要求写作法)
(2)Rt△ABC,使得Rt△ABC内接于⊙O.
21.善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形性质描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径AB⊥弦CD于点E,设AE=x,BE=y,用含x,y的式子表示图中的弦CD的长度),通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式.
22.如图,某部队在灯塔A的周围进行爆破作业,A的周围3km内的水域为危险区域,有一渔船误入离A处2km的B处,为了尽快驶离危险区域,该船应沿哪条航线方向航行?为什么?
23.如图,AB是⊙O的直径.
(1)若OD∥AC,与的大小有什么关系?为什么?
(2)把(1)中的条件和结论交换一下,还能成立吗?说明理由.
24.如图,已知梯形ABCD中,AB∥CD,AD=BC,AB=48cm,CD=30cm,高为27cm.求作一个圆经过A、B、C、D四点,求出这圆的半径.
参考答案与试题解析
一.选择题
1.解:取的中点E,连接BE、AE,如图,
∵=2,
∴==,
∴CD=AE=BE,
而AE+BE>AB,
∴AB<2CD.
故选:C.
2.解:连接CD、BE,过C点作CF∥AE交BE于点F,
点C在线段AB上,AB、AC为直径,
所以有DC⊥AE,BE⊥AE,
即得CD∥BE,且四边形DCFE为正方形,
即FC=DE=2,∠FCB=∠EAB=α,
在Rt△BCF中,BC=
故选:C.
3.解:根据题意画出图形,如图所示,EF=1dm,AB=6dm,CD=8dm,设圆的半径为r,
∵OE⊥CD,OF⊥AB,
∴CE=DE=4dm,AF=BF=3dm,
在Rt△OCE和△OAF中,
根据勾股定理得:OE==,OF==,
∴OE﹣OF=1,即﹣=1,
=+1,
两边平方得,r2﹣9=r2﹣16+2+1,
=3,
两边平方得,r2﹣16=9,
r2=25,
解得:r=5,
则圆柱形油槽直径MN为10dm.
故选:C.
4.解:C=π×8=8π,
2C=16π,
2006π=16π×125+6π,
所以停止在D点.
故选:A.
5.解:根据题意作图如右,
由图可知经过A,B两点且半径为2的圆有2个.
故选:C.
6.解:连接OA,OB,OC,OD,
∵∠BAD=50°,==,
∴∠BOD=2∠BAD=100°,
∵==,
∴AOB=∠BOC=∠COD=∠BOD=50°,
∴∠AOD=∠AOB+∠BOC+∠COD=150°,
∴∠AED=∠AOD=75°.
故选:D.
7.解:根据圆内接多边形的性质可得:矩形,正方形与等腰梯形必定存在外接圆.故选C.
8.解:如图,∵∠C=90°,
∴能完全覆盖住△ABC的最小圆为以AB为直径的圆,
由勾股定理,得AB==2,
∴圆的半径为,面积为:π()2=2π.
故选:B.
9.解:如图,m=PQ1=OP+OQ,n=PQ2=OP﹣OQ,
∴m﹣n=OP+OQ﹣(OP﹣OQ)=2OQ=10,
故选:B.
二.填空题
10.解:∵△ABC是⊙O的内接三角形,∠A=30°,
∴∠BOC=2∠A=2×30°=60°,
过点O作OD⊥BC于点D,则BD=BC=2cm,∠BOD=∠BOC=×60°=30°,
∴tan∠BOD===,解得OD=2,
∴S△OBC=BC?OD=×4×2=4cm2.
故答案为:4.
11.解:设直线AB的解析式为y=kx+b,
∵A(0,2),点B(2,0),
∴,
解得,
∴y=﹣x+2.
解方程组,得,
∴当P的坐标为(3,﹣1)时,过P,A,B三点不能作出一个圆.
故答案为(3,﹣1).
12.解:∵四边形ABCD是⊙O的内接四边形,∠B=135°,
∴∠D=45°,
故答案为:45°.
13.解:由圆心角、弧、弦的关系及圆周角定理可知:在同圆或等圆中,同弧或等弧所对圆周角
相等,
相等的圆周角所对的弧
相等,
同弧或等弧所对圆周角是其所对的圆心角的一半.
故答案为:相等、相等、一半.
14.解:如图:
在矩形ABCD中AC====10.
由图可知圆A的半径r的取值范围应大于AD的长,小于对角线AC的长,即6<r<10.
15.解:过O点作OC⊥AB,C为垂足,交⊙O于D,连OA,如图,
OA=500mm,AB=800mm,
∵OC⊥AB,
∴AC=BC=400mm,
在Rt△AOC中,OA2=AC2+OC2,
∴OC==300,
∴CD=300+500=800(mm),
即水的最大深度为800mm.
故答案为800mm.
16.解:∵D,E分别是AB,AC的中点,
∴OE⊥AC,OD⊥AB,
∵⊙O中弦AB⊥AC,
∴四边形OEAD是矩形,
(1)∵AB=AC,
∴AE=AD,
∴四边形OEAD是正方形.
(2)连接OA,
在Rt△AOD中,
∵OA=5cm,OD=3cm,
∴AD===4cm,
∴AB=2AD=8cm;
∵四边形OEAD是矩形,
∴AE=OD=3cm,
∴AC=2AE=6cm.
故答案为:正方;8,6.
17.解:∵∠AOB=2∠C=60°,OA=OB,
∴△OAB的等边三角形,
∴OA=OB=AB=4,
∴S扇形O﹣AB==π.
故答案为π.
18.解:图中直径只有AB这1条,弦有AC、AB、CD、BC这4条,以点A为端点的优弧有、这2条,劣弧有、这2条,
故答案为:1、4、2、2.
三.解答题
19.解:大圆面积为:202πcm2
小圆面积为:102πcm2
400π﹣100π=300πcm2
∴答案为300πcm2.
20.解:作法如下:
以AB的中点O为圆心,OA长为半圆画圆,则圆O即为所求作的圆.
21.解:∵直径AB⊥弦CD于点E,
∴CE=DE,
根据相交弦定理的推论,得CE2=AE?BE,则CE=,
∴CD=2CE=2.
又∵AB=x+y,且AB≥CD,
∴x+y≥2.
22.解:该船应沿航线AB方向航行离开危险区域.
理由如下:
如图,设航线AB交⊙A于点C,在⊙A上任取一点D(不包括C关于A的对称点)
连接AD、BD;
在△ABD中,
∵AB+BD>AD,AD=AC=AB+BC,
∴AB+BD>AB+BC,
∴BD>BC.
答:应沿AB的方向航行.
23.解:(1).
证明:延长DO交⊙O于E,
∵AC∥OD
∴
∵∠1=∠2
∴
∴;
(2)仍成立.
证明:延长DO交⊙O于点E,连接AD,
∵,
∴
∴∠3=∠D
∴AC∥OD.
24.解:如图所示,连接OA、OD,设其外接圆的半径是r,
则r2=OE2+AE2=OF2+DF2,
设OE=x,则OF=27﹣x,
即x2+576=(27﹣x)2+225,
解,得x=7.
则代入,得r=25(cm).
圆与正多边形-第1节
圆的基本性质》单元测试卷
一.选择题
1.在⊙O中,=2,那么
.
A.AB=2CD
B.AB=CD
C.AB<2DC
D.AB>2DC.
2.如图,点C在线段AB上,以AB、AC为直径的半圆相切于点A,大圆的弦AE交小圆于点D,∠EAB=α,如DE=2,那么BC等于( )
A.2cosα
B.2sinα
C.
D.
3.在圆柱形油槽内装有一些油,截面如图,油面宽AB为6dm,如果再注入一些油后,油面AB上升1dm,油面宽为8dm,圆柱形油槽直径MN为( )
A.6dm
B.8dm
C.10dm
D.12dm
4.如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
A.D点
B.E点
C.F点
D.G点
5.已知点A,B,且AB<4,画经过A,B两点且半径为2的圆有( )
A.0个
B.1个
C.2个
D.无数个
6.如图,==,AD为⊙O的弦,∠BAD=50°,则∠AED等于( )
A.50°
B.60°
C.70°
D.75°
7.在平行四边形、矩形、正方形、菱形、等腰梯形、直角梯形中,必定存在外接圆的有( )
A.1个
B.2个
C.3个
D.4个
8.在Rt△ABC,AB=AC=2,∠BAC=90°,能完全覆盖住此三角形的最小圆的面积是( )
A.π
B.2π
C.3π
D.4π
9.已知⊙O半径为5,OP=8,点Q在⊙O上运动,设PQ的最大值为m,最小值为n,则m﹣n的值为( )
A.5
B.10
C.12
D.8
二.填空题
10.如图,△ABC是⊙O的内接三角形,BC=4cm,∠A=30°,则△OBC的面积为
cm2.
11.已知直线l:y=x﹣4,点A(0,2),点B(2,0),设点P为直线l上一动点,当P的坐标为
时,过P,A,B三点不能作出一个圆.
12.如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠D=
.
13.在同圆或等圆中,同弧或等弧所对圆周角
,相等的圆周角所对的弧
,同弧或等弧所对圆周角是其所对的圆心角的
.
14.在矩形ABCD中,AB=8,AD=6,以A为圆心作圆,如果B,C,D三点中至少有一点在圆内,且至少有一点在圆外,则圆A的半径r的取值范围是
.
15.如图,水平放着的圆柱形排水管的截面为1000mm,其中水面宽AB=800mm,则水的最大深度为
mm.
16.如图,⊙O中弦AB⊥AC,D,E分别是AB,AC的中点.
(1)若AB=AC,则四边形OEAD是
形;
(2)若OD=3,半径r=5,则AB=
cm,AC=
cm.
17.如图,△ABC内接于⊙O,∠C=30°,AB=4,连接OA,OB,则扇形OAB的面积为
.
18.如右图中有
条直径,有
条弦,以点A为端点的优弧有
条,有劣弧
条.
三.解答题
19.如图是一个圆环,外圆半径R=20
cm,内圆半径r=10
cm,求这个圆环的面积.
20.如图已知A、B两点,
求作(1)经过A、B两点的圆⊙O;(要求写作法)
(2)Rt△ABC,使得Rt△ABC内接于⊙O.
21.善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形性质描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径AB⊥弦CD于点E,设AE=x,BE=y,用含x,y的式子表示图中的弦CD的长度),通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式.
22.如图,某部队在灯塔A的周围进行爆破作业,A的周围3km内的水域为危险区域,有一渔船误入离A处2km的B处,为了尽快驶离危险区域,该船应沿哪条航线方向航行?为什么?
23.如图,AB是⊙O的直径.
(1)若OD∥AC,与的大小有什么关系?为什么?
(2)把(1)中的条件和结论交换一下,还能成立吗?说明理由.
24.如图,已知梯形ABCD中,AB∥CD,AD=BC,AB=48cm,CD=30cm,高为27cm.求作一个圆经过A、B、C、D四点,求出这圆的半径.
参考答案与试题解析
一.选择题
1.解:取的中点E,连接BE、AE,如图,
∵=2,
∴==,
∴CD=AE=BE,
而AE+BE>AB,
∴AB<2CD.
故选:C.
2.解:连接CD、BE,过C点作CF∥AE交BE于点F,
点C在线段AB上,AB、AC为直径,
所以有DC⊥AE,BE⊥AE,
即得CD∥BE,且四边形DCFE为正方形,
即FC=DE=2,∠FCB=∠EAB=α,
在Rt△BCF中,BC=
故选:C.
3.解:根据题意画出图形,如图所示,EF=1dm,AB=6dm,CD=8dm,设圆的半径为r,
∵OE⊥CD,OF⊥AB,
∴CE=DE=4dm,AF=BF=3dm,
在Rt△OCE和△OAF中,
根据勾股定理得:OE==,OF==,
∴OE﹣OF=1,即﹣=1,
=+1,
两边平方得,r2﹣9=r2﹣16+2+1,
=3,
两边平方得,r2﹣16=9,
r2=25,
解得:r=5,
则圆柱形油槽直径MN为10dm.
故选:C.
4.解:C=π×8=8π,
2C=16π,
2006π=16π×125+6π,
所以停止在D点.
故选:A.
5.解:根据题意作图如右,
由图可知经过A,B两点且半径为2的圆有2个.
故选:C.
6.解:连接OA,OB,OC,OD,
∵∠BAD=50°,==,
∴∠BOD=2∠BAD=100°,
∵==,
∴AOB=∠BOC=∠COD=∠BOD=50°,
∴∠AOD=∠AOB+∠BOC+∠COD=150°,
∴∠AED=∠AOD=75°.
故选:D.
7.解:根据圆内接多边形的性质可得:矩形,正方形与等腰梯形必定存在外接圆.故选C.
8.解:如图,∵∠C=90°,
∴能完全覆盖住△ABC的最小圆为以AB为直径的圆,
由勾股定理,得AB==2,
∴圆的半径为,面积为:π()2=2π.
故选:B.
9.解:如图,m=PQ1=OP+OQ,n=PQ2=OP﹣OQ,
∴m﹣n=OP+OQ﹣(OP﹣OQ)=2OQ=10,
故选:B.
二.填空题
10.解:∵△ABC是⊙O的内接三角形,∠A=30°,
∴∠BOC=2∠A=2×30°=60°,
过点O作OD⊥BC于点D,则BD=BC=2cm,∠BOD=∠BOC=×60°=30°,
∴tan∠BOD===,解得OD=2,
∴S△OBC=BC?OD=×4×2=4cm2.
故答案为:4.
11.解:设直线AB的解析式为y=kx+b,
∵A(0,2),点B(2,0),
∴,
解得,
∴y=﹣x+2.
解方程组,得,
∴当P的坐标为(3,﹣1)时,过P,A,B三点不能作出一个圆.
故答案为(3,﹣1).
12.解:∵四边形ABCD是⊙O的内接四边形,∠B=135°,
∴∠D=45°,
故答案为:45°.
13.解:由圆心角、弧、弦的关系及圆周角定理可知:在同圆或等圆中,同弧或等弧所对圆周角
相等,
相等的圆周角所对的弧
相等,
同弧或等弧所对圆周角是其所对的圆心角的一半.
故答案为:相等、相等、一半.
14.解:如图:
在矩形ABCD中AC====10.
由图可知圆A的半径r的取值范围应大于AD的长,小于对角线AC的长,即6<r<10.
15.解:过O点作OC⊥AB,C为垂足,交⊙O于D,连OA,如图,
OA=500mm,AB=800mm,
∵OC⊥AB,
∴AC=BC=400mm,
在Rt△AOC中,OA2=AC2+OC2,
∴OC==300,
∴CD=300+500=800(mm),
即水的最大深度为800mm.
故答案为800mm.
16.解:∵D,E分别是AB,AC的中点,
∴OE⊥AC,OD⊥AB,
∵⊙O中弦AB⊥AC,
∴四边形OEAD是矩形,
(1)∵AB=AC,
∴AE=AD,
∴四边形OEAD是正方形.
(2)连接OA,
在Rt△AOD中,
∵OA=5cm,OD=3cm,
∴AD===4cm,
∴AB=2AD=8cm;
∵四边形OEAD是矩形,
∴AE=OD=3cm,
∴AC=2AE=6cm.
故答案为:正方;8,6.
17.解:∵∠AOB=2∠C=60°,OA=OB,
∴△OAB的等边三角形,
∴OA=OB=AB=4,
∴S扇形O﹣AB==π.
故答案为π.
18.解:图中直径只有AB这1条,弦有AC、AB、CD、BC这4条,以点A为端点的优弧有、这2条,劣弧有、这2条,
故答案为:1、4、2、2.
三.解答题
19.解:大圆面积为:202πcm2
小圆面积为:102πcm2
400π﹣100π=300πcm2
∴答案为300πcm2.
20.解:作法如下:
以AB的中点O为圆心,OA长为半圆画圆,则圆O即为所求作的圆.
21.解:∵直径AB⊥弦CD于点E,
∴CE=DE,
根据相交弦定理的推论,得CE2=AE?BE,则CE=,
∴CD=2CE=2.
又∵AB=x+y,且AB≥CD,
∴x+y≥2.
22.解:该船应沿航线AB方向航行离开危险区域.
理由如下:
如图,设航线AB交⊙A于点C,在⊙A上任取一点D(不包括C关于A的对称点)
连接AD、BD;
在△ABD中,
∵AB+BD>AD,AD=AC=AB+BC,
∴AB+BD>AB+BC,
∴BD>BC.
答:应沿AB的方向航行.
23.解:(1).
证明:延长DO交⊙O于E,
∵AC∥OD
∴
∵∠1=∠2
∴
∴;
(2)仍成立.
证明:延长DO交⊙O于点E,连接AD,
∵,
∴
∴∠3=∠D
∴AC∥OD.
24.解:如图所示,连接OA、OD,设其外接圆的半径是r,
则r2=OE2+AE2=OF2+DF2,
设OE=x,则OF=27﹣x,
即x2+576=(27﹣x)2+225,
解,得x=7.
则代入,得r=25(cm).
