2020-2021学年 九年级下册数学 鲁教五四新版 第5章 圆 单元测试题(Word版 含解析)
文档属性
| 名称 | 2020-2021学年 九年级下册数学 鲁教五四新版 第5章 圆 单元测试题(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 270.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 00:00:00 | ||
图片预览

文档简介
2020-2021学年九年级下册数学鲁教五四新版《第5章
圆》单元测试题
一.选择题
1.以已知点O为圆心,已知线段a为半径作圆,可以作( )
A.1个
B.2个
C.3个
D.无数个
2.半圆的圆心角( )
A.大于180°
B.等于180°
C.在90°~180°之间
D.等于90°
3.如图,∠B=58°,则∠OCA=( )
A.25°
B.30°
C.32°
D.20°
4.下列说法正确的是( )
A.三点确定一个圆
B.圆心角的度数等于圆周角的两倍
C.与半径垂直的直线是圆的切线
D.在同圆或等圆中,相等的圆周角所对的弦、弧分别相等
5.已知正三角形的边长为6,则其内切圆的半径为( )
A.
B.3
C.
D.1
6.下列命题中真命题是( )
A.两个等腰三角形一定全等
B.正多边形的每一个内角的度数随边数增多而减少
C.菱形既是中心对称图形,又是轴对称图形
D.两直线平行,同旁内角相等
7.一条圆弧所对的圆心角等于240°,它的长度等于半径为4cm的圆的周长,则这条弧所在的半径为( )
A.3cm
B.4cm
C.5cm
D.6cm
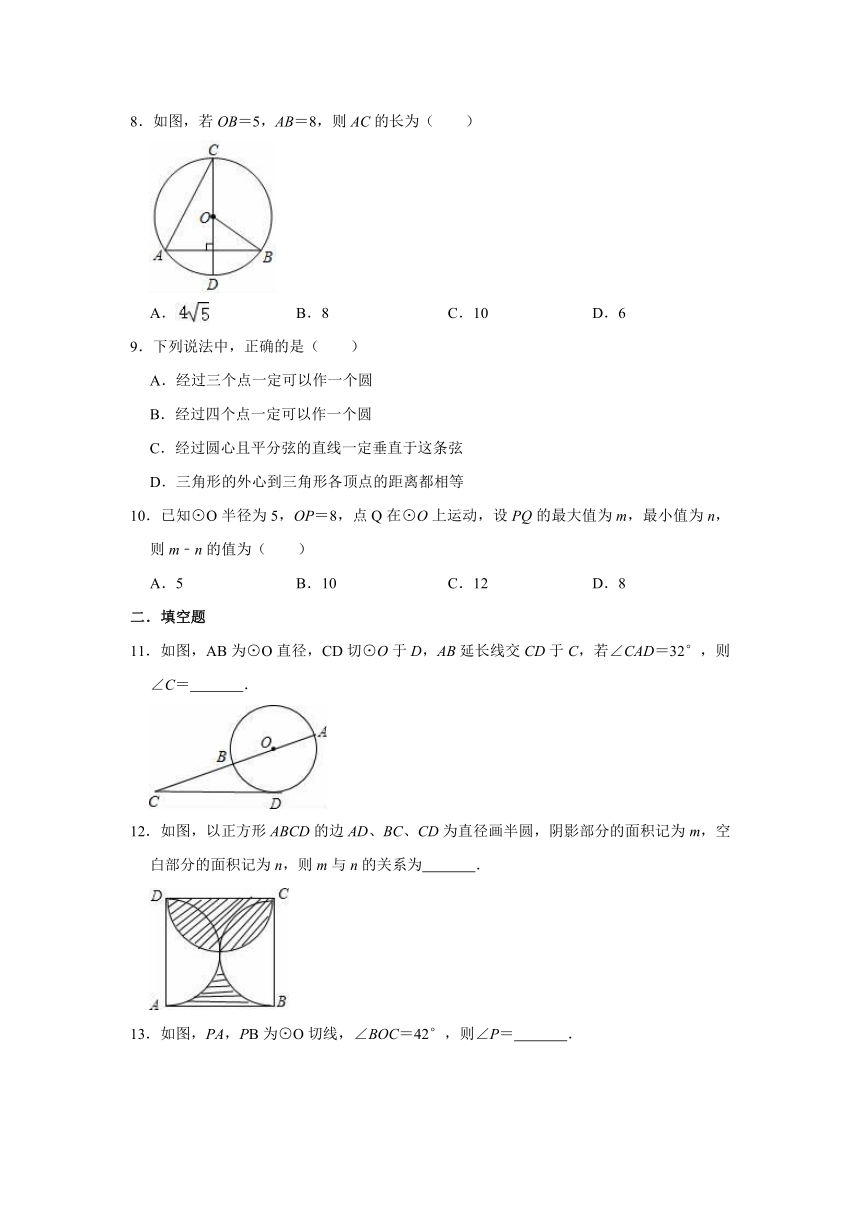
8.如图,若OB=5,AB=8,则AC的长为( )
A.
B.8
C.10
D.6
9.下列说法中,正确的是( )
A.经过三个点一定可以作一个圆
B.经过四个点一定可以作一个圆
C.经过圆心且平分弦的直线一定垂直于这条弦
D.三角形的外心到三角形各顶点的距离都相等
10.已知⊙O半径为5,OP=8,点Q在⊙O上运动,设PQ的最大值为m,最小值为n,则m﹣n的值为( )
A.5
B.10
C.12
D.8
二.填空题
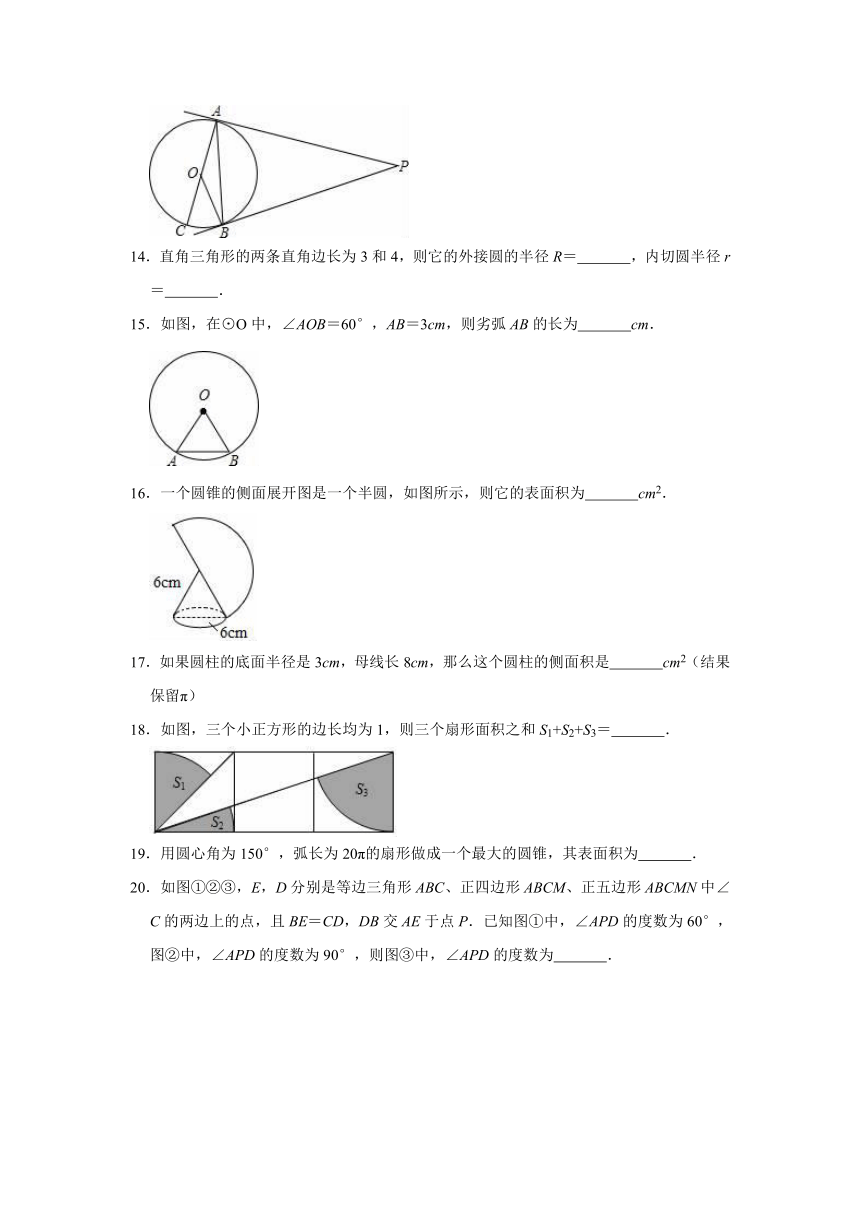
11.如图,AB为⊙O直径,CD切⊙O于D,AB延长线交CD于C,若∠CAD=32°,则∠C=
.
12.如图,以正方形ABCD的边AD、BC、CD为直径画半圆,阴影部分的面积记为m,空白部分的面积记为n,则m与n的关系为
.
13.如图,PA,PB为⊙O切线,∠BOC=42°,则∠P=
.
14.直角三角形的两条直角边长为3和4,则它的外接圆的半径R=
,内切圆半径r=
.
15.如图,在⊙O中,∠AOB=60°,AB=3cm,则劣弧AB的长为
cm.
16.一个圆锥的侧面展开图是一个半圆,如图所示,则它的表面积为
cm2.
17.如果圆柱的底面半径是3cm,母线长8cm,那么这个圆柱的侧面积是
cm2(结果保留π)
18.如图,三个小正方形的边长均为1,则三个扇形面积之和S1+S2+S3=
.
19.用圆心角为150°,弧长为20π的扇形做成一个最大的圆锥,其表面积为
.
20.如图①②③,E,D分别是等边三角形ABC、正四边形ABCM、正五边形ABCMN中∠C的两边上的点,且BE=CD,DB交AE于点P.已知图①中,∠APD的度数为60°,图②中,∠APD的度数为90°,则图③中,∠APD的度数为
.
三.解答题
21.如图,△ABC中,∠C是直角,AB=12cm,∠ABC=60°,将△ABC以点B为中心顺时针旋转,使点C旋转到AB的延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是多少?(π=3.14159…,最后结果保留三个有效数字)
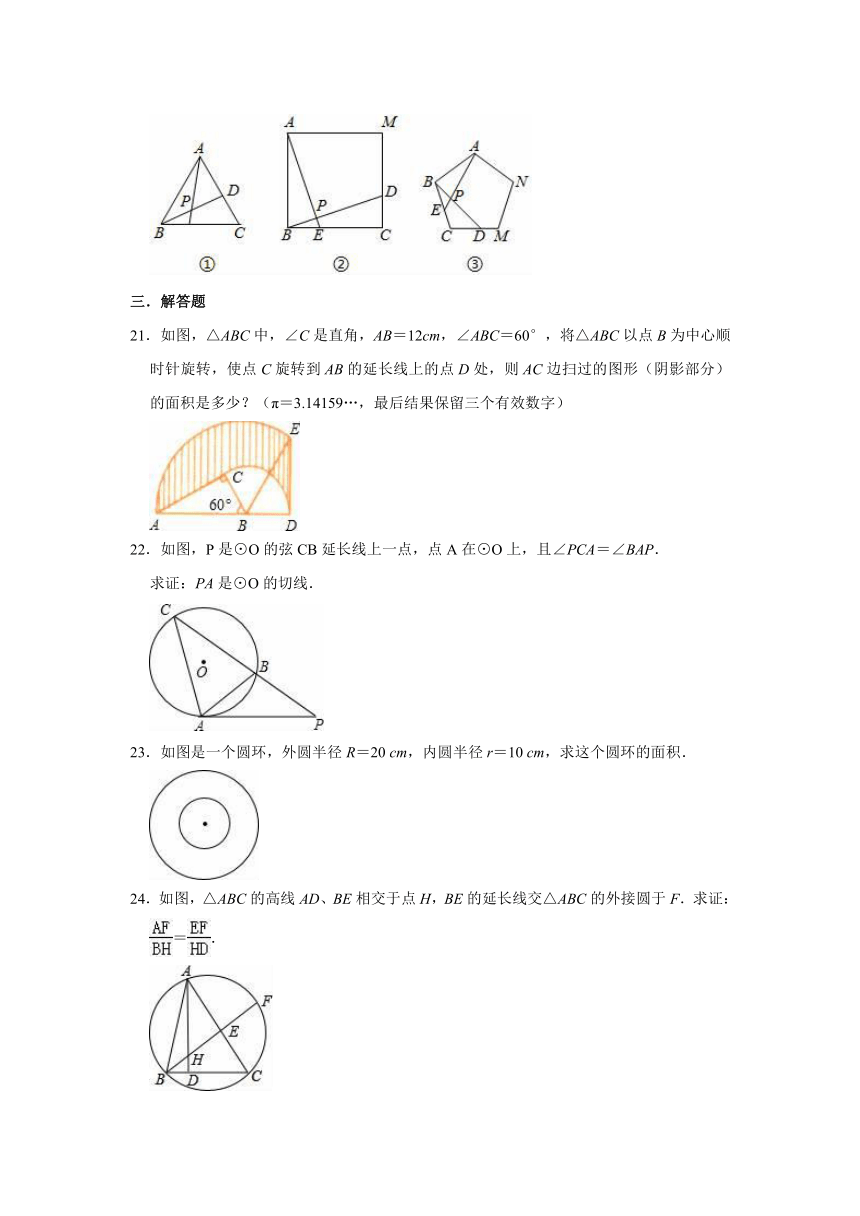
22.如图,P是⊙O的弦CB延长线上一点,点A在⊙O上,且∠PCA=∠BAP.
求证:PA是⊙O的切线.
23.如图是一个圆环,外圆半径R=20
cm,内圆半径r=10
cm,求这个圆环的面积.
24.如图,△ABC的高线AD、BE相交于点H,BE的延长线交△ABC的外接圆于F.求证:=.
25.如图,在Rt△ABC中,∠ACB=90°,AD是△ABC的角平分线,过A、C、D三点的圆O与斜边AB交于点E,连接DE.
求证:DC=DE.
26.(综合题)如图所示,⊙O中的弦AB,CD互相垂直于E,AE=5cm,BE=13cm,O到AB的距离为2cm,求⊙O的半径及O到CD的距离.
27.已知如图,圆锥的底面半径为3cm,母线长为9cm,C是母线PB中点且在圆锥的侧面上,求从A到C的最短距离为多少厘米?
参考答案与试题解析
一.选择题
1.解:到定点距离等于定长的点只有一个,即以定点为圆心,定长为半径的圆.
故选:A.
2.解:∵半圆所对的弦是直径
∴半圆所对的圆心角是180度.
故选:B.
3.解:连接OA,
∵∠B=58°,
∴∠AOC=2∠B=116°.
∵OA=OC,
∴∠OAC=∠OCA==32°.故选C.
4.解:A、不在同一直线上的三点确定一个圆;故A错误.
B、在同圆或等圆中,同弧或等弧所对的圆心角的度数等于圆周角的两倍;故B错误.
C、经过半径外端且垂直于半径的直线是圆的切线;故C错误.
D、在同圆或等圆中,相等的圆周角所对的弦、弧分别相等;故D正确.
故选:D.
5.解:⊙O是边长为6的等边三角形ABC的内切圆,如图,
连AO且交BC于D,则OA平分∠BAC,
又∵△ABC是等边三角形,
∴AO垂直平分BC,即D为切点.则OD为内切圆半径.
连接OB,在直角三角形BOD中,则有BD=3,∠OBD=30°,
∴OD=tan30°×BD=3×=.
故选:C.
6.解:A、假命题,因为如图所示:AD=AE,AB=AC,但△ADE与△ABC不全等;
B、假命题,因为任何多边形的外角和均为360°,则其每个外角为α=,可见,当n增大时,α减小;
C、真命题,因为菱形的对角线是其对称轴,两条对角线的交点是对称中心;
D、假命题,因为两直线平行,同旁内角互补.
故选:C.
7.解:设这条弧所在的半径为xcm,则=2π×4,
解得:x=6,
故选:D.
8.解:CD垂直AB于E,如图,则AE=BE=AB=×8=4,
在Rt△OBE中,OE===3,
∴CE=OE+OC=3+5=8,
在Rt△ACE中,AC===4.
故选:A.
9.解:A选项错,正确的是不在同一直线上的三个点确定一个圆;
B选项错,经过不在一直线上的四个点不一定能做圆,除非这四点共圆;
C选项错,过圆心的直径所在的直线都平分直径(平分弦),却不一定垂直这条直径;
只有D选项正确,外心是三边垂直平分线的交点,线段垂直平分线上的点到线段两端的距离相等,所以,三角形的外心到三角形各顶点的距离都相等.
故选:D.
10.解:如图,m=PQ1=OP+OQ,n=PQ2=OP﹣OQ,
∴m﹣n=OP+OQ﹣(OP﹣OQ)=2OQ=10,
故选:B.
二.填空题
11.解:连接OD、AD,如图所示:
由题意可得:OD⊥CD,
∵OA=OD,
∴∠CAD=∠ODA=32°,
∴∠COD=∠CAD+∠ODA=64°;
∵∠COD+∠C=90°,
∴∠C=26°,
故此题应该填26°.
12.解:设正方形ABCD的边长为a,
则阴影AEB的面积=(S□ABCD﹣S半圆AED﹣S半圆BEC)÷2=[a2﹣2××()2π]÷2=﹣,
S阴影=m=S半圆CDE+S阴影AEB=×+﹣=,
故n=a2﹣m=a2﹣=.
故答案为:m=n.
13.解:∵PA,PB为⊙O切线,
∴OA⊥AP,OB⊥BP,
∴∠P=180°﹣∠AOB;
∵∠AOB=180°﹣∠BOC,
∴∠P=∠BOC=42°,
故此题应该填42°.
14.解:直角三角形的两条直角边长为3和4,则其斜边为5,
所以它的外接圆半径R=×5=2.5,内切圆半径r==1.
15.解:∵∠AOB=60°,AB=3cm,
∴三角形OAB是等边三角形,
∴圆的半径是3厘米,
则劣弧AB的长为:=π(cm),
答:劣弧AB的长为πcm.
故答案为:π.
16.解:根据题意,圆锥的表面积=π×32+×2π×3×6=27π(cm2).
故答案为27π.
17.解:圆柱的侧面展开图的面积是:π×2×3×8=48π(cm2).
故答案为:48π.
18.解:S1+S2+S3=+=π.
故答案为π.
19.解:设圆锥的母线长为R.
=20π,
解得:R=24,
圆锥的底面半径为:20π÷2π=10,
∴表面积为π×10×24+π×102=340π.
20.解:正五边形各内角相等,则∠ABE=∠BCD
在△ABE和△BCD中,
,
∴△ABE≌△BCD(SAS),
∴∠EBP=∠BAE,
∴∠APD=∠BPE=180°﹣∠EBP﹣∠BEP
∵∠EBP=∠BAE,
∴∠APD=180°﹣∠BAE﹣∠BEP=∠ABE.
∵正五边形各内角均为108°,
∴∠APD=108°.
故答案为:108°.
三.解答题
21.解:∵△ABC中,∠C是直角,AB=12cm,∠ABC=60°
∴AC=6cm,BC=6cm
∵将△ABC以点B为中心顺时针旋转,使点C旋转到AB的延长线上的点D处
∴△ABC≌△EBD
由题给图象可知:
S阴影=S扇形ABE+S△BDE﹣S△ABC﹣S扇形BCD
=
=
答:AC边扫过的图形(阴影部分)的面积约是113cm2.
22.证明:作⊙O的直径AD,连接BD.
则∠C=∠D(同弧所对的圆周角相等),∠ABD=90°(直径所对的圆周角是直角),
∴∠D+∠BAD=90°,
∴∠C+∠BAD=90°(等量代换);
又∵∠PCA=∠BAP,
∴∠BAD+∠PAB=90°,即AP⊥AD,
∴PA是⊙O的切线.
23.解:大圆面积为:202πcm2
小圆面积为:102πcm2
400π﹣100π=300πcm2
∴答案为300πcm2.
24.解:连AF,如图,
∵AD,BE都是三角形的高,
∴∠BDH=∠AEF=90°.
又∵∠1=∠2,
∴△AEF∽△BDH.
∴=.
25.证明∵∠ACB=90°,
∴AD为直径,
又∵AD是△ABC的角平分线,
∴∠CAD=∠EAD,
∴,
∴CD=DE.
26.解:AB=AE+BE=5+13=18(cm),
连接OB,过O作OM⊥AB,
∴AM=AB=9(cm),
又∵OM=2(cm),
∴在Rt△OBM中,
BO====11cm,
ON=EM=AM﹣AE=9﹣5=4(cm).
27.解:圆锥的底面周长是6π,则6π=,
∴n=120°,
即圆锥侧面展开图的圆心角是120°,
∴∠APB=60°,
∵PA=PB,
∴△PAB是等边三角形,
∵C是PB中点,
∴AC⊥PB,
∴∠ACP=90°,
∵在圆锥侧面展开图中AP=9,PC=4.5,
∴在圆锥侧面展开图中AC==cm.
最短距离是cm.
圆》单元测试题
一.选择题
1.以已知点O为圆心,已知线段a为半径作圆,可以作( )
A.1个
B.2个
C.3个
D.无数个
2.半圆的圆心角( )
A.大于180°
B.等于180°
C.在90°~180°之间
D.等于90°
3.如图,∠B=58°,则∠OCA=( )
A.25°
B.30°
C.32°
D.20°
4.下列说法正确的是( )
A.三点确定一个圆
B.圆心角的度数等于圆周角的两倍
C.与半径垂直的直线是圆的切线
D.在同圆或等圆中,相等的圆周角所对的弦、弧分别相等
5.已知正三角形的边长为6,则其内切圆的半径为( )
A.
B.3
C.
D.1
6.下列命题中真命题是( )
A.两个等腰三角形一定全等
B.正多边形的每一个内角的度数随边数增多而减少
C.菱形既是中心对称图形,又是轴对称图形
D.两直线平行,同旁内角相等
7.一条圆弧所对的圆心角等于240°,它的长度等于半径为4cm的圆的周长,则这条弧所在的半径为( )
A.3cm
B.4cm
C.5cm
D.6cm
8.如图,若OB=5,AB=8,则AC的长为( )
A.
B.8
C.10
D.6
9.下列说法中,正确的是( )
A.经过三个点一定可以作一个圆
B.经过四个点一定可以作一个圆
C.经过圆心且平分弦的直线一定垂直于这条弦
D.三角形的外心到三角形各顶点的距离都相等
10.已知⊙O半径为5,OP=8,点Q在⊙O上运动,设PQ的最大值为m,最小值为n,则m﹣n的值为( )
A.5
B.10
C.12
D.8
二.填空题
11.如图,AB为⊙O直径,CD切⊙O于D,AB延长线交CD于C,若∠CAD=32°,则∠C=
.
12.如图,以正方形ABCD的边AD、BC、CD为直径画半圆,阴影部分的面积记为m,空白部分的面积记为n,则m与n的关系为
.
13.如图,PA,PB为⊙O切线,∠BOC=42°,则∠P=
.
14.直角三角形的两条直角边长为3和4,则它的外接圆的半径R=
,内切圆半径r=
.
15.如图,在⊙O中,∠AOB=60°,AB=3cm,则劣弧AB的长为
cm.
16.一个圆锥的侧面展开图是一个半圆,如图所示,则它的表面积为
cm2.
17.如果圆柱的底面半径是3cm,母线长8cm,那么这个圆柱的侧面积是
cm2(结果保留π)
18.如图,三个小正方形的边长均为1,则三个扇形面积之和S1+S2+S3=
.
19.用圆心角为150°,弧长为20π的扇形做成一个最大的圆锥,其表面积为
.
20.如图①②③,E,D分别是等边三角形ABC、正四边形ABCM、正五边形ABCMN中∠C的两边上的点,且BE=CD,DB交AE于点P.已知图①中,∠APD的度数为60°,图②中,∠APD的度数为90°,则图③中,∠APD的度数为
.
三.解答题
21.如图,△ABC中,∠C是直角,AB=12cm,∠ABC=60°,将△ABC以点B为中心顺时针旋转,使点C旋转到AB的延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是多少?(π=3.14159…,最后结果保留三个有效数字)
22.如图,P是⊙O的弦CB延长线上一点,点A在⊙O上,且∠PCA=∠BAP.
求证:PA是⊙O的切线.
23.如图是一个圆环,外圆半径R=20
cm,内圆半径r=10
cm,求这个圆环的面积.
24.如图,△ABC的高线AD、BE相交于点H,BE的延长线交△ABC的外接圆于F.求证:=.
25.如图,在Rt△ABC中,∠ACB=90°,AD是△ABC的角平分线,过A、C、D三点的圆O与斜边AB交于点E,连接DE.
求证:DC=DE.
26.(综合题)如图所示,⊙O中的弦AB,CD互相垂直于E,AE=5cm,BE=13cm,O到AB的距离为2cm,求⊙O的半径及O到CD的距离.
27.已知如图,圆锥的底面半径为3cm,母线长为9cm,C是母线PB中点且在圆锥的侧面上,求从A到C的最短距离为多少厘米?
参考答案与试题解析
一.选择题
1.解:到定点距离等于定长的点只有一个,即以定点为圆心,定长为半径的圆.
故选:A.
2.解:∵半圆所对的弦是直径
∴半圆所对的圆心角是180度.
故选:B.
3.解:连接OA,
∵∠B=58°,
∴∠AOC=2∠B=116°.
∵OA=OC,
∴∠OAC=∠OCA==32°.故选C.
4.解:A、不在同一直线上的三点确定一个圆;故A错误.
B、在同圆或等圆中,同弧或等弧所对的圆心角的度数等于圆周角的两倍;故B错误.
C、经过半径外端且垂直于半径的直线是圆的切线;故C错误.
D、在同圆或等圆中,相等的圆周角所对的弦、弧分别相等;故D正确.
故选:D.
5.解:⊙O是边长为6的等边三角形ABC的内切圆,如图,
连AO且交BC于D,则OA平分∠BAC,
又∵△ABC是等边三角形,
∴AO垂直平分BC,即D为切点.则OD为内切圆半径.
连接OB,在直角三角形BOD中,则有BD=3,∠OBD=30°,
∴OD=tan30°×BD=3×=.
故选:C.
6.解:A、假命题,因为如图所示:AD=AE,AB=AC,但△ADE与△ABC不全等;
B、假命题,因为任何多边形的外角和均为360°,则其每个外角为α=,可见,当n增大时,α减小;
C、真命题,因为菱形的对角线是其对称轴,两条对角线的交点是对称中心;
D、假命题,因为两直线平行,同旁内角互补.
故选:C.
7.解:设这条弧所在的半径为xcm,则=2π×4,
解得:x=6,
故选:D.
8.解:CD垂直AB于E,如图,则AE=BE=AB=×8=4,
在Rt△OBE中,OE===3,
∴CE=OE+OC=3+5=8,
在Rt△ACE中,AC===4.
故选:A.
9.解:A选项错,正确的是不在同一直线上的三个点确定一个圆;
B选项错,经过不在一直线上的四个点不一定能做圆,除非这四点共圆;
C选项错,过圆心的直径所在的直线都平分直径(平分弦),却不一定垂直这条直径;
只有D选项正确,外心是三边垂直平分线的交点,线段垂直平分线上的点到线段两端的距离相等,所以,三角形的外心到三角形各顶点的距离都相等.
故选:D.
10.解:如图,m=PQ1=OP+OQ,n=PQ2=OP﹣OQ,
∴m﹣n=OP+OQ﹣(OP﹣OQ)=2OQ=10,
故选:B.
二.填空题
11.解:连接OD、AD,如图所示:
由题意可得:OD⊥CD,
∵OA=OD,
∴∠CAD=∠ODA=32°,
∴∠COD=∠CAD+∠ODA=64°;
∵∠COD+∠C=90°,
∴∠C=26°,
故此题应该填26°.
12.解:设正方形ABCD的边长为a,
则阴影AEB的面积=(S□ABCD﹣S半圆AED﹣S半圆BEC)÷2=[a2﹣2××()2π]÷2=﹣,
S阴影=m=S半圆CDE+S阴影AEB=×+﹣=,
故n=a2﹣m=a2﹣=.
故答案为:m=n.
13.解:∵PA,PB为⊙O切线,
∴OA⊥AP,OB⊥BP,
∴∠P=180°﹣∠AOB;
∵∠AOB=180°﹣∠BOC,
∴∠P=∠BOC=42°,
故此题应该填42°.
14.解:直角三角形的两条直角边长为3和4,则其斜边为5,
所以它的外接圆半径R=×5=2.5,内切圆半径r==1.
15.解:∵∠AOB=60°,AB=3cm,
∴三角形OAB是等边三角形,
∴圆的半径是3厘米,
则劣弧AB的长为:=π(cm),
答:劣弧AB的长为πcm.
故答案为:π.
16.解:根据题意,圆锥的表面积=π×32+×2π×3×6=27π(cm2).
故答案为27π.
17.解:圆柱的侧面展开图的面积是:π×2×3×8=48π(cm2).
故答案为:48π.
18.解:S1+S2+S3=+=π.
故答案为π.
19.解:设圆锥的母线长为R.
=20π,
解得:R=24,
圆锥的底面半径为:20π÷2π=10,
∴表面积为π×10×24+π×102=340π.
20.解:正五边形各内角相等,则∠ABE=∠BCD
在△ABE和△BCD中,
,
∴△ABE≌△BCD(SAS),
∴∠EBP=∠BAE,
∴∠APD=∠BPE=180°﹣∠EBP﹣∠BEP
∵∠EBP=∠BAE,
∴∠APD=180°﹣∠BAE﹣∠BEP=∠ABE.
∵正五边形各内角均为108°,
∴∠APD=108°.
故答案为:108°.
三.解答题
21.解:∵△ABC中,∠C是直角,AB=12cm,∠ABC=60°
∴AC=6cm,BC=6cm
∵将△ABC以点B为中心顺时针旋转,使点C旋转到AB的延长线上的点D处
∴△ABC≌△EBD
由题给图象可知:
S阴影=S扇形ABE+S△BDE﹣S△ABC﹣S扇形BCD
=
=
答:AC边扫过的图形(阴影部分)的面积约是113cm2.
22.证明:作⊙O的直径AD,连接BD.
则∠C=∠D(同弧所对的圆周角相等),∠ABD=90°(直径所对的圆周角是直角),
∴∠D+∠BAD=90°,
∴∠C+∠BAD=90°(等量代换);
又∵∠PCA=∠BAP,
∴∠BAD+∠PAB=90°,即AP⊥AD,
∴PA是⊙O的切线.
23.解:大圆面积为:202πcm2
小圆面积为:102πcm2
400π﹣100π=300πcm2
∴答案为300πcm2.
24.解:连AF,如图,
∵AD,BE都是三角形的高,
∴∠BDH=∠AEF=90°.
又∵∠1=∠2,
∴△AEF∽△BDH.
∴=.
25.证明∵∠ACB=90°,
∴AD为直径,
又∵AD是△ABC的角平分线,
∴∠CAD=∠EAD,
∴,
∴CD=DE.
26.解:AB=AE+BE=5+13=18(cm),
连接OB,过O作OM⊥AB,
∴AM=AB=9(cm),
又∵OM=2(cm),
∴在Rt△OBM中,
BO====11cm,
ON=EM=AM﹣AE=9﹣5=4(cm).
27.解:圆锥的底面周长是6π,则6π=,
∴n=120°,
即圆锥侧面展开图的圆心角是120°,
∴∠APB=60°,
∵PA=PB,
∴△PAB是等边三角形,
∵C是PB中点,
∴AC⊥PB,
∴∠ACP=90°,
∵在圆锥侧面展开图中AP=9,PC=4.5,
∴在圆锥侧面展开图中AC==cm.
最短距离是cm.
