六年级下册数学课件-2.3 对比圆柱与圆锥 西师大版
文档属性
| 名称 | 六年级下册数学课件-2.3 对比圆柱与圆锥 西师大版 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
六年级数学下册
对比圆柱和圆锥
2.4
对比圆柱与圆锥
第2单元
圆柱和
圆锥
学习目标
理解圆柱和圆锥的关系,进一步掌握圆柱和圆锥体积的计算方法。
认识圆柱和圆锥知识在生活中的运用,提高分析问题、解决问题的能力。
复习导入
圆柱体、圆锥体的特征对比表格:
复习导入
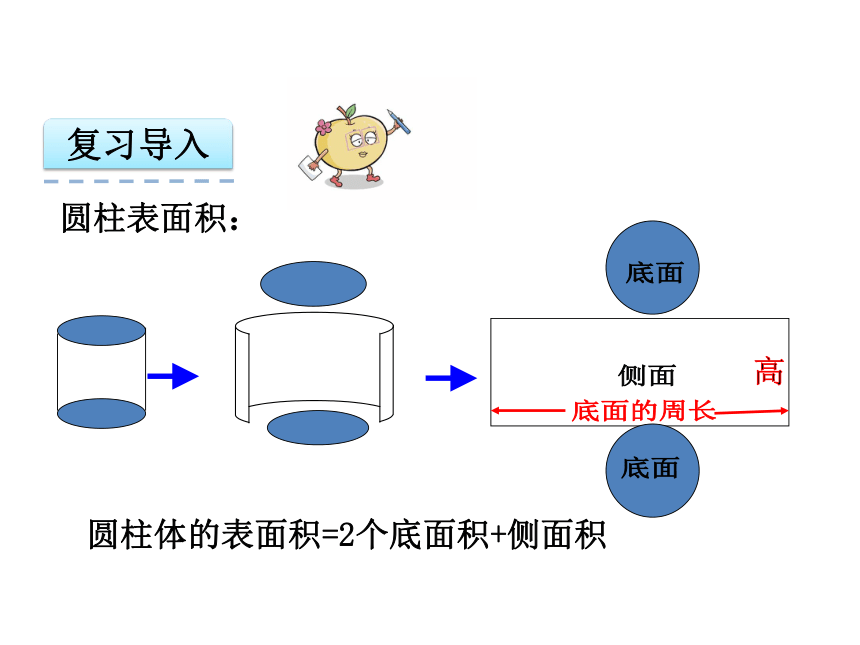
圆柱表面积:
侧面
底面的周长
高
底面
底面
圆柱体的表面积=2个底面积+侧面积
复习导入
用字母表示的圆柱圆锥的计算公式:
复习导入
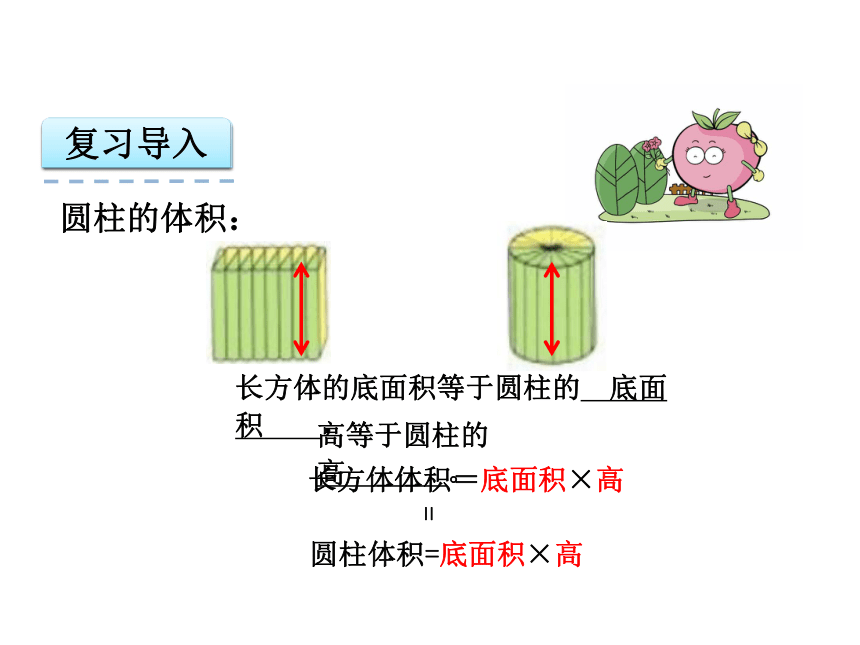
长方体体积=底面积×高
圆柱体积=底面积×高
=
长方体的底面积等于圆柱的
底面积
,
高等于圆柱的
高
。
圆柱的体积:
探索新知
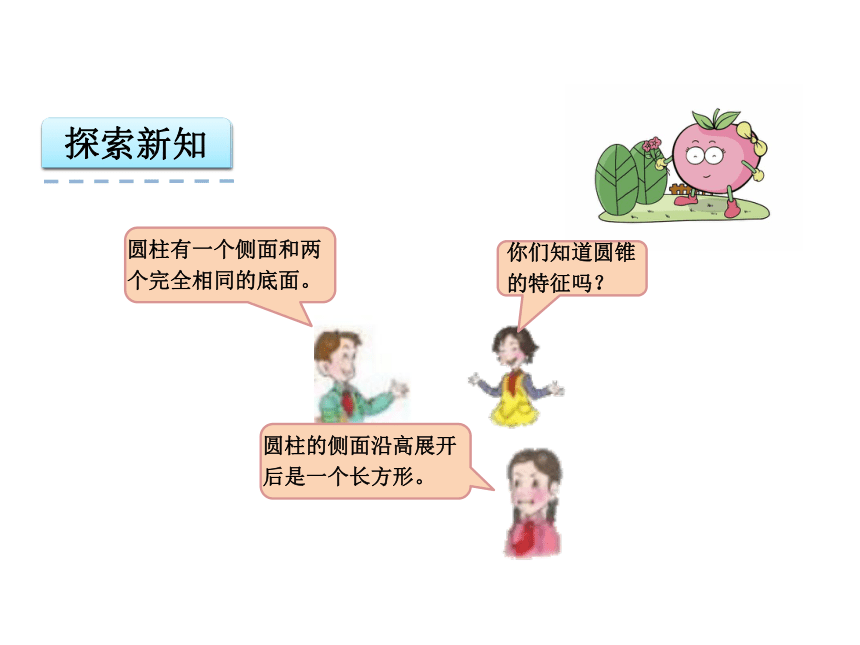
圆柱有一个侧面和两个完全相同的底面。
你们知道圆锥的特征吗?
圆柱的侧面沿高展开后是一个长方形。
探索新知
圆锥的侧面展开是一个扇形,底面是一个圆形。
探索新知
算一算:
(1)计算圆柱的表面积和体积。
C=31.4dm
h=8dm
r=31.4÷2π=5dm
S底=π×52×2=157dm2
S侧=31.4×8=251.2dm2
S表=157
+
251.2=408.2dm2
V=s底×h=78.5×8=628m3
探索新知
算一算:
(2)计算圆锥体积。
r=5dm
h=8dm
V=
×3.14×52×8
=
×628
=
dm3
探索新知
对比完成的两道题,你有什么发现?
这两个图形的半径相等,高相等。也就是等底等高。从结果上可以看出,圆柱的体积是628立方分米,圆锥的体积则为
立方分米,由此,我们再一次可以得出:等底等高的圆锥体积=
圆柱的体积。
探索新知
计算圆锥体积。
d=12cm
h=15cm
=
565.2
cm3
V=
×3.14×(12÷2)2×15
=
×1695.6
探索新知
r=6dm
h=5dm
=188.4
dm3
计算圆锥体积。
V=
×3.14×62×5
=
×565.2
典题精讲
在一个半径是10厘米的圆柱形容器中,
放入一个圆锥形铁块,全部浸没在水中,这时水面上升0.6厘米。
①这个圆锥形铁块的体积是(
)立方厘米
0.6厘米
A.
B.
C.
解题思路:
圆锥铁块的体积实际就是上升的那一部分水的体积,即是底面半径为10厘米,高为0.6厘米的圆柱的体积。
答案:
应该选择B。
B
典题精讲
0.6厘米
②若这个圆锥形铁块的高为6厘米,它的底面积是(
)平方厘米。
D.
31.4
F.
94.2
E.
314
解题思路:
这是一道已知圆锥体积和高,求底面积的逆思维题型。可以用方程解答,也可以用算术方法解答。用算术方法解答时要记得先转化成等底等高的圆柱,也就是乘以3。
典题精讲
解答过程:
设:圆锥的底面积为x。
χ×6=188.4
=
=188.4÷6
χ
χ
=31.4
=94.2平方厘米
χ
典题精讲
0.6厘米
②若这个圆锥形铁块的高为6厘米,它的底面积是(
)平方厘米。
D.
31.4
F.
94.2
E.
314
F
答案:
应该选择F。
易错提醒
将一个棱长为2分米的正方体削成一个最大的圆柱体,圆柱的侧面积是多少平方分米?
易错分析:此题隐藏的条件比较多,学生比较难以理解,会出现很多孩子束手无策的情况,听话的孩子担心没有书写就会乱凑数据,瞎编出来的结果是可以想象得到的。
易错提醒
S侧=πdh=3.14×2×2=12.56
圆柱的底面直径是(
)分米
圆柱的高是(
)分米
2
2
将一个棱长为2分米的正方体削成一个最大的圆柱体,圆柱的侧面积是多少平方分米?
2分米
答:圆柱的侧面积是12.56平方分米。
正确解答
学以致用
一个圆柱形的水池,直径是20米,深2米。
1、这个水池占地面积是多少?
2、挖成这个水池,共需要挖土多少立方米?
3、在池内的侧面和池底抹一层水泥,水泥面的面积是多少平方米?
3.14×(20÷2)2=314(
平方米)
3.14×(20÷2)2×2=628(立方米)
3.14×(20÷2)2+
3.14×20
×
2=439.6(平方米)
学以致用
晒谷场上一个圆锥形小麦堆,底面周长是18.84米,高1米。
1、这个小麦堆的体积是多少立方米?
18.84÷3.14÷2=3(
米)
半径:
答:这个小麦队的体积是9.42立方米。
体积:
×3.14×32×
1=9.42(立方米)
学以致用
2、如果每立方米小麦约重700千克,这堆小麦重多少千克?
9.42×700=6594(千克)
答:这堆小麦重6594千克。
课堂
总结
通过这节课的学习,你有什么收获?
要计算圆柱和圆锥的体积需要知道
哪些条件,怎样计算。
解决问题时先读懂题,再判断所求
问题与过去哪些知识有联系,再选择方法。
谢谢
六年级数学下册
对比圆柱和圆锥
2.4
对比圆柱与圆锥
第2单元
圆柱和
圆锥
学习目标
理解圆柱和圆锥的关系,进一步掌握圆柱和圆锥体积的计算方法。
认识圆柱和圆锥知识在生活中的运用,提高分析问题、解决问题的能力。
复习导入
圆柱体、圆锥体的特征对比表格:
复习导入
圆柱表面积:
侧面
底面的周长
高
底面
底面
圆柱体的表面积=2个底面积+侧面积
复习导入
用字母表示的圆柱圆锥的计算公式:
复习导入
长方体体积=底面积×高
圆柱体积=底面积×高
=
长方体的底面积等于圆柱的
底面积
,
高等于圆柱的
高
。
圆柱的体积:
探索新知
圆柱有一个侧面和两个完全相同的底面。
你们知道圆锥的特征吗?
圆柱的侧面沿高展开后是一个长方形。
探索新知
圆锥的侧面展开是一个扇形,底面是一个圆形。
探索新知
算一算:
(1)计算圆柱的表面积和体积。
C=31.4dm
h=8dm
r=31.4÷2π=5dm
S底=π×52×2=157dm2
S侧=31.4×8=251.2dm2
S表=157
+
251.2=408.2dm2
V=s底×h=78.5×8=628m3
探索新知
算一算:
(2)计算圆锥体积。
r=5dm
h=8dm
V=
×3.14×52×8
=
×628
=
dm3
探索新知
对比完成的两道题,你有什么发现?
这两个图形的半径相等,高相等。也就是等底等高。从结果上可以看出,圆柱的体积是628立方分米,圆锥的体积则为
立方分米,由此,我们再一次可以得出:等底等高的圆锥体积=
圆柱的体积。
探索新知
计算圆锥体积。
d=12cm
h=15cm
=
565.2
cm3
V=
×3.14×(12÷2)2×15
=
×1695.6
探索新知
r=6dm
h=5dm
=188.4
dm3
计算圆锥体积。
V=
×3.14×62×5
=
×565.2
典题精讲
在一个半径是10厘米的圆柱形容器中,
放入一个圆锥形铁块,全部浸没在水中,这时水面上升0.6厘米。
①这个圆锥形铁块的体积是(
)立方厘米
0.6厘米
A.
B.
C.
解题思路:
圆锥铁块的体积实际就是上升的那一部分水的体积,即是底面半径为10厘米,高为0.6厘米的圆柱的体积。
答案:
应该选择B。
B
典题精讲
0.6厘米
②若这个圆锥形铁块的高为6厘米,它的底面积是(
)平方厘米。
D.
31.4
F.
94.2
E.
314
解题思路:
这是一道已知圆锥体积和高,求底面积的逆思维题型。可以用方程解答,也可以用算术方法解答。用算术方法解答时要记得先转化成等底等高的圆柱,也就是乘以3。
典题精讲
解答过程:
设:圆锥的底面积为x。
χ×6=188.4
=
=188.4÷6
χ
χ
=31.4
=94.2平方厘米
χ
典题精讲
0.6厘米
②若这个圆锥形铁块的高为6厘米,它的底面积是(
)平方厘米。
D.
31.4
F.
94.2
E.
314
F
答案:
应该选择F。
易错提醒
将一个棱长为2分米的正方体削成一个最大的圆柱体,圆柱的侧面积是多少平方分米?
易错分析:此题隐藏的条件比较多,学生比较难以理解,会出现很多孩子束手无策的情况,听话的孩子担心没有书写就会乱凑数据,瞎编出来的结果是可以想象得到的。
易错提醒
S侧=πdh=3.14×2×2=12.56
圆柱的底面直径是(
)分米
圆柱的高是(
)分米
2
2
将一个棱长为2分米的正方体削成一个最大的圆柱体,圆柱的侧面积是多少平方分米?
2分米
答:圆柱的侧面积是12.56平方分米。
正确解答
学以致用
一个圆柱形的水池,直径是20米,深2米。
1、这个水池占地面积是多少?
2、挖成这个水池,共需要挖土多少立方米?
3、在池内的侧面和池底抹一层水泥,水泥面的面积是多少平方米?
3.14×(20÷2)2=314(
平方米)
3.14×(20÷2)2×2=628(立方米)
3.14×(20÷2)2+
3.14×20
×
2=439.6(平方米)
学以致用
晒谷场上一个圆锥形小麦堆,底面周长是18.84米,高1米。
1、这个小麦堆的体积是多少立方米?
18.84÷3.14÷2=3(
米)
半径:
答:这个小麦队的体积是9.42立方米。
体积:
×3.14×32×
1=9.42(立方米)
学以致用
2、如果每立方米小麦约重700千克,这堆小麦重多少千克?
9.42×700=6594(千克)
答:这堆小麦重6594千克。
课堂
总结
通过这节课的学习,你有什么收获?
要计算圆柱和圆锥的体积需要知道
哪些条件,怎样计算。
解决问题时先读懂题,再判断所求
问题与过去哪些知识有联系,再选择方法。
谢谢
