用二分法求方程的近似解
图片预览



文档简介
(共29张PPT)
*
*
方程f(x)=0有实数根
函数y=f(x)有零点
1、方程实根与对应函数零点之间的联系
*
2、函数零点所在区间的判定
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a) ·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c ∈(a,b),使得f(c)=0,这个 c 也就是方程f(x)=0的根。
*
近似值与精确值的误差容许范围的大小
也叫步长,是区间两端点的距离的大小
*
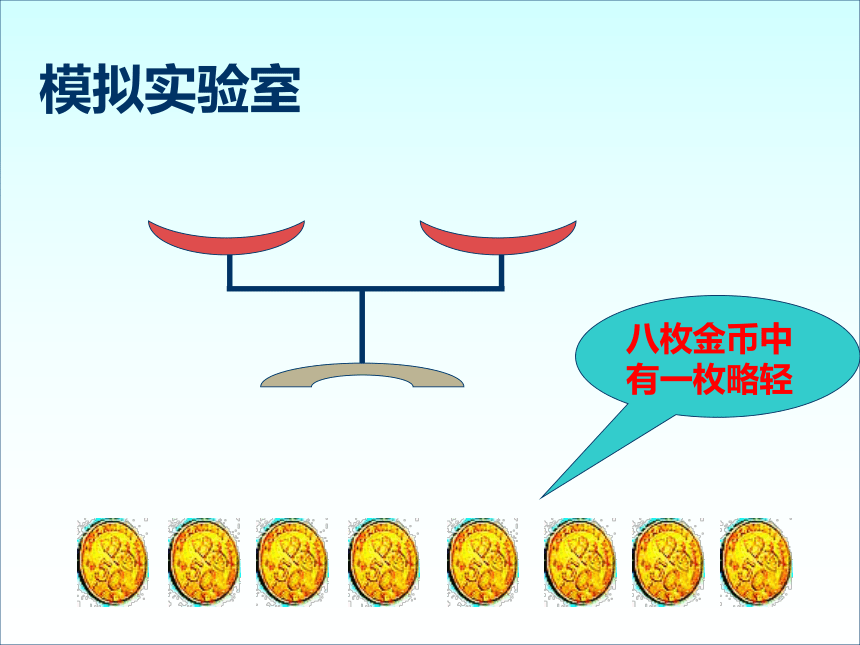
模拟实验室
八枚金币中有一枚略轻
*
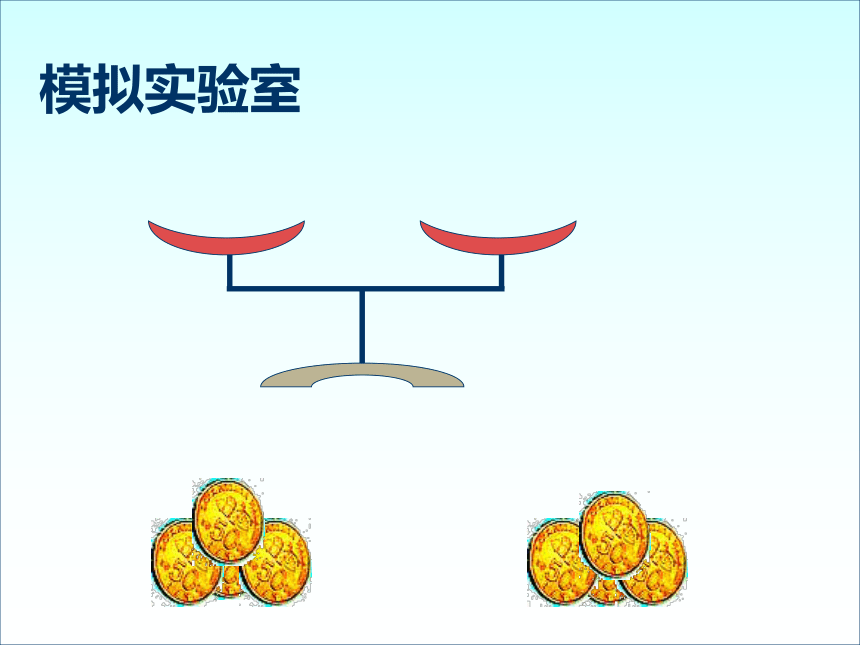
模拟实验室
*
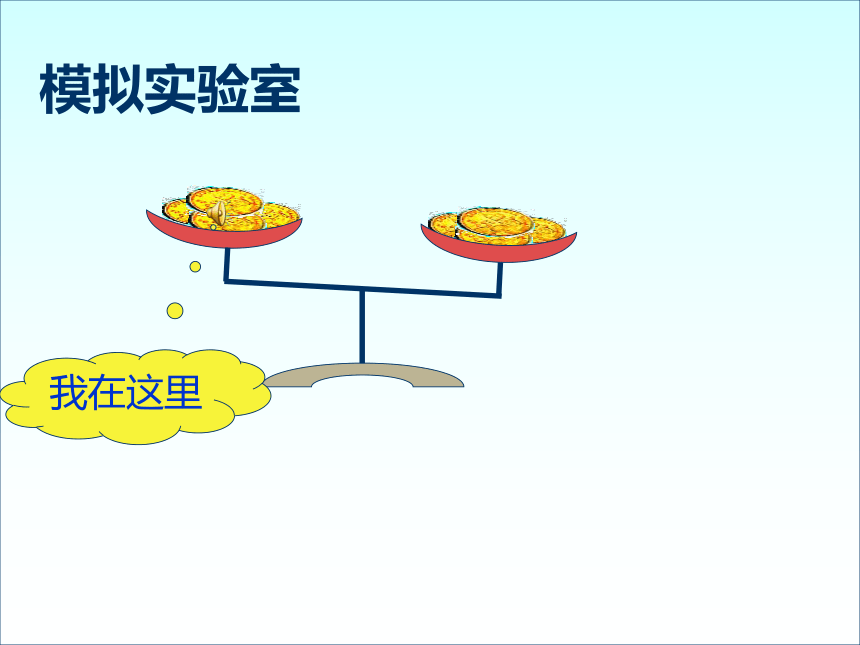
模拟实验室
我在这里
*
模拟实验室
*
模拟实验室
*
模拟实验室
我在这里
*
模拟实验室
*
模拟实验室
哦,找到了啊!
通过这个小实验,你能想到什么样的方法寻找方程的近似解?
*
区间两端点和的一半
区间(a,b)的中点为
*
求方程lnx+2x-6=0在(2,3)内的近似解(精确度为0.1)
解:
设函数f(x)=lnx+2x-6,
则函数零点的值即为所求方程的解。
方法
,f(2.75) ≈0.512>0
,f(2.5) ≈-0.084<0
由于f(2)≈-1.3069<0, f(3) ≈ 1.0986>0
即f(2)· f(3)<0,
所以函数在区间(2,3)内有零点x0
取
则x0∈(2.5,3)
即f(2.5)· f(3) <0
取
则x0∈(2.5,2.75)
即f(2.5)· f(2.75) <0
2+3
=2.5
2
2.5+3
=2.75
2
*
返回
,f(2.625) ≈0.215>0
取
则x0∈(2.5,2.625)
即f(2.5)· f(2.625) <0
取
则x0∈(2.5,2.5625)
即f(2.5)· f(2.5625) <0
而|2.5-2.5625|=0.0625<0.1
所以我们可以取2.5作为方程lnx+2x-6=0的近似值。
2.5+2.75
=2.625
2
2.5+2.625
=2.5625
2
,f(2.5625) ≈0.066>0
*
对于在区间[a,b]上连续不断且f(a) ·f(b)<0的函数 y=f(x) ,通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逼近零点,进而得到零点近似值。
*
对于在①区间[a,b]上连续不断且f(a) ·f(b)<0的函数 y=f(x) ,通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逼近零点,进而得到零点近似值。
根基
*
对于在①区间[a,b]上连续不断且f(a) ·f(b)<0的函数 y=f(x) ,通过②不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逼近零点,进而得到零点近似值。
根基
主干
*
对于在①区间[a,b]上连续不断且f(a) ·f(b)<0的函数 y=f(x) ,通过②不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逼近零点,进而③得到零点近似值。
根基
主干
终端
*
设函数
定区间(a,b)
取中点c
判断中点函数值的符号
若f(c)=0,则函数的零点x0=c;
若f (a) · f(c)<0,则 x0∈(a,c)(令b=c);
若f (c) · f(b)<0,则 x0∈(c,b)(令a=c) ;
重复操作,逐步缩小零点所在区间的长度,直到这个长度小于题目给定的精确度
取出最终得到的区间内的任意一个值作为所求方程的近似解
*
借助计算器或计算机,用二分法求方程-x3-3x+5=0在区间(1,2)内的近似解(精确度0.1)。
*
解:
借助计算器或计算机,可求得
f(1)=1>0,f(2)=-9<0
于是有 f(1)·f(2)<0
即函数f(x)= -x3-3x+5 在区间(1,2)内有零点
设函数f(x)= -x3-3x+5 ,
则函数零点的值即为所求方程的解。
*
借助计算器或计算机,列出表格
1.5
-2.875
(1,1.5)
1.25
-0.70
(1,1.25)
1.125
(1.125,1.25)
(1.125,1.1875)
1.1875
0.20
-0.24
1
0.5
0.25
0.125
0.0625
*
由表格知函数零点在区间(1.125,1.1875)内
而|1.125-1.1875|=0.0625<0.1
则函数零点的近似值可取1.125。
*
*
求方程的近似解
目标:
方法:
二分法
解题过程:
*
设函数
定区间(a,b)
取中点c
判断中点函数值的符号
若f(c)=0,则函数的零点x0=c;
若f (a) · f(c)<0,则 x0∈(a,c)(令b=c);
若f (c) · f(b)<0,则 x0∈(c,b) (令a=c) ;
重复操作,逐步缩小零点所在区间的长度,直到这个长度小于题目给定的精确度
取出最终得到的区间内的任意一个值作为所求方程的近似解
*
课本
P92 A组 3,4,5
*
*
*
方程f(x)=0有实数根
函数y=f(x)有零点
1、方程实根与对应函数零点之间的联系
*
2、函数零点所在区间的判定
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a) ·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c ∈(a,b),使得f(c)=0,这个 c 也就是方程f(x)=0的根。
*
近似值与精确值的误差容许范围的大小
也叫步长,是区间两端点的距离的大小
*
模拟实验室
八枚金币中有一枚略轻
*
模拟实验室
*
模拟实验室
我在这里
*
模拟实验室
*
模拟实验室
*
模拟实验室
我在这里
*
模拟实验室
*
模拟实验室
哦,找到了啊!
通过这个小实验,你能想到什么样的方法寻找方程的近似解?
*
区间两端点和的一半
区间(a,b)的中点为
*
求方程lnx+2x-6=0在(2,3)内的近似解(精确度为0.1)
解:
设函数f(x)=lnx+2x-6,
则函数零点的值即为所求方程的解。
方法
,f(2.75) ≈0.512>0
,f(2.5) ≈-0.084<0
由于f(2)≈-1.3069<0, f(3) ≈ 1.0986>0
即f(2)· f(3)<0,
所以函数在区间(2,3)内有零点x0
取
则x0∈(2.5,3)
即f(2.5)· f(3) <0
取
则x0∈(2.5,2.75)
即f(2.5)· f(2.75) <0
2+3
=2.5
2
2.5+3
=2.75
2
*
返回
,f(2.625) ≈0.215>0
取
则x0∈(2.5,2.625)
即f(2.5)· f(2.625) <0
取
则x0∈(2.5,2.5625)
即f(2.5)· f(2.5625) <0
而|2.5-2.5625|=0.0625<0.1
所以我们可以取2.5作为方程lnx+2x-6=0的近似值。
2.5+2.75
=2.625
2
2.5+2.625
=2.5625
2
,f(2.5625) ≈0.066>0
*
对于在区间[a,b]上连续不断且f(a) ·f(b)<0的函数 y=f(x) ,通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逼近零点,进而得到零点近似值。
*
对于在①区间[a,b]上连续不断且f(a) ·f(b)<0的函数 y=f(x) ,通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逼近零点,进而得到零点近似值。
根基
*
对于在①区间[a,b]上连续不断且f(a) ·f(b)<0的函数 y=f(x) ,通过②不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逼近零点,进而得到零点近似值。
根基
主干
*
对于在①区间[a,b]上连续不断且f(a) ·f(b)<0的函数 y=f(x) ,通过②不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逼近零点,进而③得到零点近似值。
根基
主干
终端
*
设函数
定区间(a,b)
取中点c
判断中点函数值的符号
若f(c)=0,则函数的零点x0=c;
若f (a) · f(c)<0,则 x0∈(a,c)(令b=c);
若f (c) · f(b)<0,则 x0∈(c,b)(令a=c) ;
重复操作,逐步缩小零点所在区间的长度,直到这个长度小于题目给定的精确度
取出最终得到的区间内的任意一个值作为所求方程的近似解
*
借助计算器或计算机,用二分法求方程-x3-3x+5=0在区间(1,2)内的近似解(精确度0.1)。
*
解:
借助计算器或计算机,可求得
f(1)=1>0,f(2)=-9<0
于是有 f(1)·f(2)<0
即函数f(x)= -x3-3x+5 在区间(1,2)内有零点
设函数f(x)= -x3-3x+5 ,
则函数零点的值即为所求方程的解。
*
借助计算器或计算机,列出表格
1.5
-2.875
(1,1.5)
1.25
-0.70
(1,1.25)
1.125
(1.125,1.25)
(1.125,1.1875)
1.1875
0.20
-0.24
1
0.5
0.25
0.125
0.0625
*
由表格知函数零点在区间(1.125,1.1875)内
而|1.125-1.1875|=0.0625<0.1
则函数零点的近似值可取1.125。
*
*
求方程的近似解
目标:
方法:
二分法
解题过程:
*
设函数
定区间(a,b)
取中点c
判断中点函数值的符号
若f(c)=0,则函数的零点x0=c;
若f (a) · f(c)<0,则 x0∈(a,c)(令b=c);
若f (c) · f(b)<0,则 x0∈(c,b) (令a=c) ;
重复操作,逐步缩小零点所在区间的长度,直到这个长度小于题目给定的精确度
取出最终得到的区间内的任意一个值作为所求方程的近似解
*
课本
P92 A组 3,4,5
*
