2020-2021北师大版九年级数学下册第一章 1.1-1.2 同步练习题(word版含答案)
文档属性
| 名称 | 2020-2021北师大版九年级数学下册第一章 1.1-1.2 同步练习题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 176.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 14:53:44 | ||
图片预览


文档简介
2020-2021学年北师大版九年级数学下册第一章
1.1-1.2
同步练习题
一、选择题
1.如图,在Rt△ABC中,∠C=90°,AC=,AB=4,则sinA的值是(
)
A.
B.
C.
D.
2.如图,在△ABC中,∠C=90°,BC=2AC,则cosA=(
)
A.
B.
C.
D.
3.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D.若BD∶CD=3∶2,则tanB=(
)
A.
B.
C.
D.
4.如图,在矩形ABCD中,AB=2,BC=2,E是BC的中点,将△ABE沿直线AE翻折,点B落在点F处,连接CF,则cos∠ECF的值为(
)
A.
B.
C.
D.
二、填空题
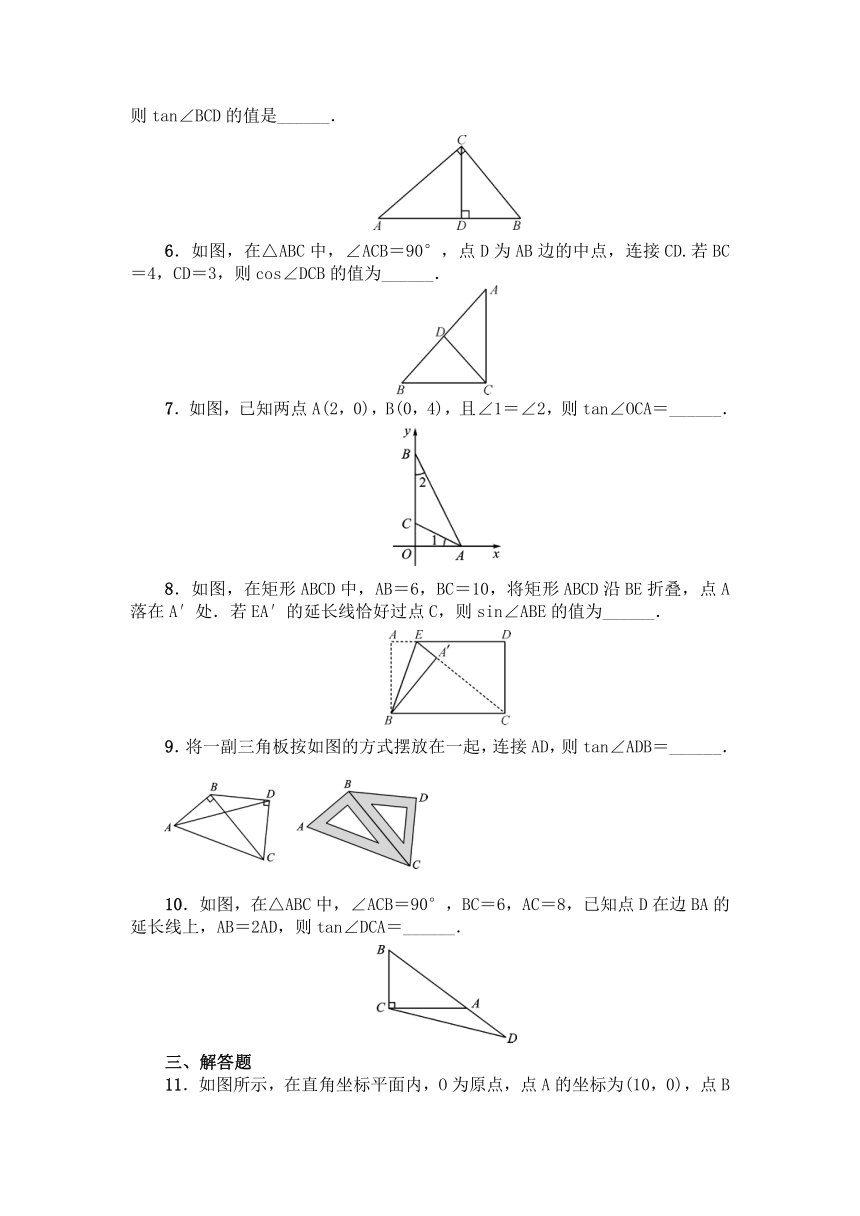
5.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是______.
6.如图,在△ABC中,∠ACB=90°,点D为AB边的中点,连接CD.若BC=4,CD=3,则cos∠DCB的值为______.
7.如图,已知两点A(2,0),B(0,4),且∠1=∠2,则tan∠OCA=______.
8.如图,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A′处.若EA′的延长线恰好过点C,则sin∠ABE的值为______.
9.将一副三角板按如图的方式摆放在一起,连接AD,则tan∠ADB=______.
10.如图,在△ABC中,∠ACB=90°,BC=6,AC=8,已知点D在边BA的延长线上,AB=2AD,则tan∠DCA=______.
三、解答题
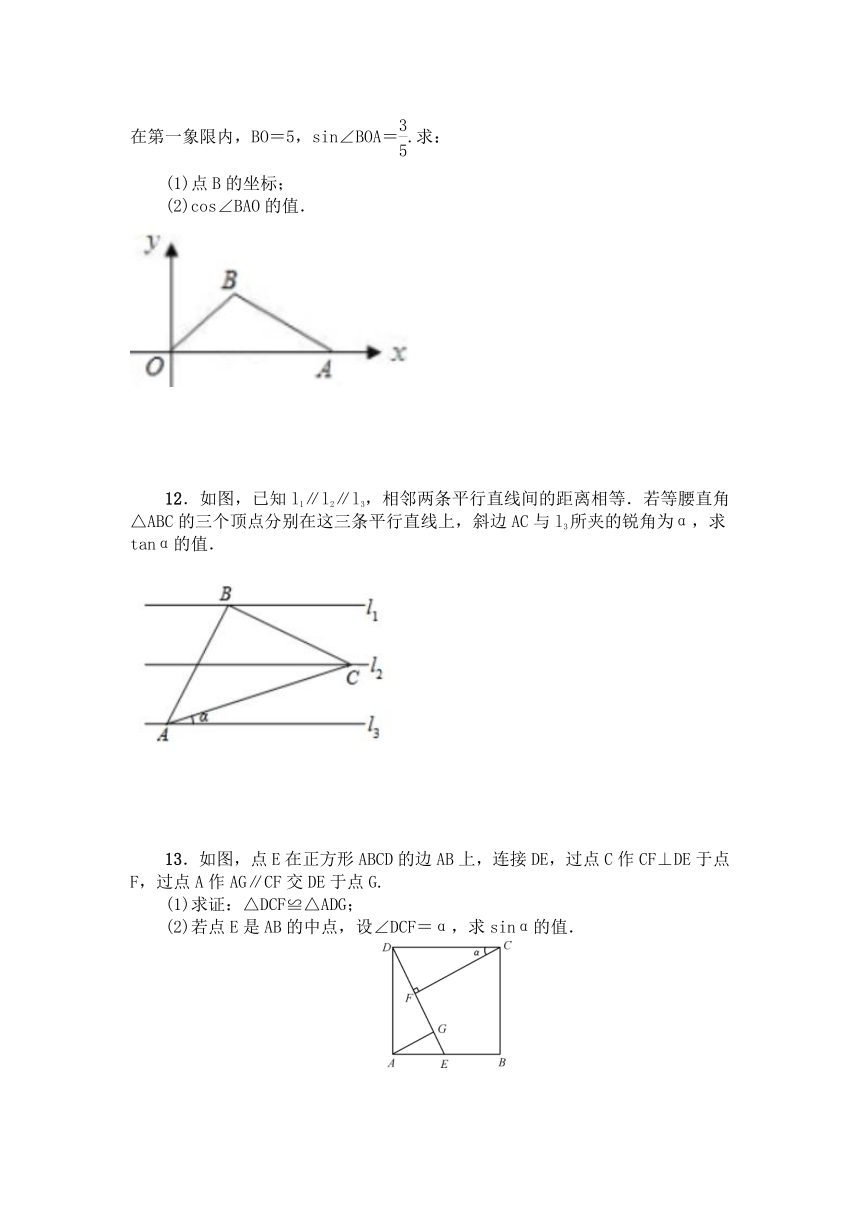
11.如图所示,在直角坐标平面内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.求:
(1)点B的坐标;
(2)cos∠BAO的值.
12.如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等.若等腰直角△ABC的三个顶点分别在这三条平行直线上,斜边AC与l3所夹的锐角为α,求tanα的值.
13.如图,点E在正方形ABCD的边AB上,连接DE,过点C作CF⊥DE于点F,过点A作AG∥CF交DE于点G.
(1)求证:△DCF≌△ADG;
(2)若点E是AB的中点,设∠DCF=α,求sinα的值.
14.如图,在4×4的网格中,每个小正方形的边长为1,线段AB,CD的端点均为格点.
(1)AB的长度为2,CD的长度为______;
(2)若AB与CD所夹锐角为α,求tanα的值.
参考答案
2020-2021学年北师大版九年级数学下册
1.1-1.2
同步练习题
一、选择题
1.如图,在Rt△ABC中,∠C=90°,AC=,AB=4,则sinA的值是(D)
A.
B.
C.
D.
2.如图,在△ABC中,∠C=90°,BC=2AC,则cosA=(D)
A.
B.
C.
D.
3.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D.若BD∶CD=3∶2,则tanB=(D)
A.
B.
C.
D.
4.如图,在矩形ABCD中,AB=2,BC=2,E是BC的中点,将△ABE沿直线AE翻折,点B落在点F处,连接CF,则cos∠ECF的值为(C)
A.
B.
C.
D.
二、填空题
5.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是.
6.如图,在△ABC中,∠ACB=90°,点D为AB边的中点,连接CD.若BC=4,CD=3,则cos∠DCB的值为.
7.如图,已知两点A(2,0),B(0,4),且∠1=∠2,则tan∠OCA=2.
8.如图,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A′处.若EA′的延长线恰好过点C,则sin∠ABE的值为.
9.将一副三角板按如图的方式摆放在一起,连接AD,则tan∠ADB=.
10.如图,在△ABC中,∠ACB=90°,BC=6,AC=8,已知点D在边BA的延长线上,AB=2AD,则tan∠DCA=.
三、解答题
11.如图所示,在直角坐标平面内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.求:
(1)点B的坐标;
(2)cos∠BAO的值.
解:(1)过点B作BH⊥OA于点H,
在Rt△OHB中,∵BO=5,
sin∠BOA=,
∴BH=3.∴OH==4.
∴点B的坐标为(4,3).
(2)∵OA=10,OH=4,∴AH=6.
在Rt△AHB中,∵BH=3,
∴AB==3.
∴cos∠BAO==.
12.如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等.若等腰直角△ABC的三个顶点分别在这三条平行直线上,斜边AC与l3所夹的锐角为α,求tanα的值.
解:过点A作l1的垂线,垂足为D,过点C作l1,l3的垂线,垂足为E,F,
设l1,l2之间的距离为a,
则l2与l3之间的距离也为a.
∵∠ABC=90°,∴∠DBA+∠EBC=90°.
∵∠DBA+∠DAB=90°,∴∠EBC=∠DAB.
又∵∠ADB=∠BEC,AB=BC,
∴△ADB≌△BEC(AAS).
∴AD=BE=2a,DB=EC=a.
∴AF=DE=3a.
∴tanα===.
13.如图,点E在正方形ABCD的边AB上,连接DE,过点C作CF⊥DE于点F,过点A作AG∥CF交DE于点G.
(1)求证:△DCF≌△ADG;
(2)若点E是AB的中点,设∠DCF=α,求sinα的值.
解:(1)证明:在正方形ABCD中,AD=DC,
∠ADC=90°,
∵CF⊥DE,
∴∠CFD=∠CFG=90°.
∵AG∥CF,
∴∠AGD=∠CFG=90°.
∴∠AGD=∠CFD.
∵∠ADG+∠CDE=∠ADC=90°,
∠DCF+∠CDE=90°,
∴∠ADG=∠DCF.
在△DCF和△ADG中,
∴△DCF≌△ADG(AAS).
(2)设正方形ABCD的边长为2a.
∵点E是AB的中点,
∴AE=×2a=a.
在Rt△ADE中,DE===a,
∴sin∠ADG===.
∵∠ADG=∠DCF=α,
∴sinα=.
14.如图,在4×4的网格中,每个小正方形的边长为1,线段AB,CD的端点均为格点.
(1)AB的长度为2,CD的长度为;
(2)若AB与CD所夹锐角为α,求tanα的值.
解:取格点E,连接CE,使CE∥AB,取格点F,连接EF,交CD于点G,取格点H,使CH=2,
∵∠CHD=∠EDF=90°,HD=DF=3,CH=DE=3,
∴△CHD≌△EDF(SAS).
∴∠EDG=∠EFD.
又∵∠GED=∠DEF,∴△DEG∽△FED.
∴==,即==.
∴EG=,DG=.
∴CG=CD-DG=.
∴tan∠ECG==.
∵AB∥CE,∴α=∠ECG.
∴tanα=.
1.1-1.2
同步练习题
一、选择题
1.如图,在Rt△ABC中,∠C=90°,AC=,AB=4,则sinA的值是(
)
A.
B.
C.
D.
2.如图,在△ABC中,∠C=90°,BC=2AC,则cosA=(
)
A.
B.
C.
D.
3.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D.若BD∶CD=3∶2,则tanB=(
)
A.
B.
C.
D.
4.如图,在矩形ABCD中,AB=2,BC=2,E是BC的中点,将△ABE沿直线AE翻折,点B落在点F处,连接CF,则cos∠ECF的值为(
)
A.
B.
C.
D.
二、填空题
5.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是______.
6.如图,在△ABC中,∠ACB=90°,点D为AB边的中点,连接CD.若BC=4,CD=3,则cos∠DCB的值为______.
7.如图,已知两点A(2,0),B(0,4),且∠1=∠2,则tan∠OCA=______.
8.如图,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A′处.若EA′的延长线恰好过点C,则sin∠ABE的值为______.
9.将一副三角板按如图的方式摆放在一起,连接AD,则tan∠ADB=______.
10.如图,在△ABC中,∠ACB=90°,BC=6,AC=8,已知点D在边BA的延长线上,AB=2AD,则tan∠DCA=______.
三、解答题
11.如图所示,在直角坐标平面内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.求:
(1)点B的坐标;
(2)cos∠BAO的值.
12.如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等.若等腰直角△ABC的三个顶点分别在这三条平行直线上,斜边AC与l3所夹的锐角为α,求tanα的值.
13.如图,点E在正方形ABCD的边AB上,连接DE,过点C作CF⊥DE于点F,过点A作AG∥CF交DE于点G.
(1)求证:△DCF≌△ADG;
(2)若点E是AB的中点,设∠DCF=α,求sinα的值.
14.如图,在4×4的网格中,每个小正方形的边长为1,线段AB,CD的端点均为格点.
(1)AB的长度为2,CD的长度为______;
(2)若AB与CD所夹锐角为α,求tanα的值.
参考答案
2020-2021学年北师大版九年级数学下册
1.1-1.2
同步练习题
一、选择题
1.如图,在Rt△ABC中,∠C=90°,AC=,AB=4,则sinA的值是(D)
A.
B.
C.
D.
2.如图,在△ABC中,∠C=90°,BC=2AC,则cosA=(D)
A.
B.
C.
D.
3.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D.若BD∶CD=3∶2,则tanB=(D)
A.
B.
C.
D.
4.如图,在矩形ABCD中,AB=2,BC=2,E是BC的中点,将△ABE沿直线AE翻折,点B落在点F处,连接CF,则cos∠ECF的值为(C)
A.
B.
C.
D.
二、填空题
5.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是.
6.如图,在△ABC中,∠ACB=90°,点D为AB边的中点,连接CD.若BC=4,CD=3,则cos∠DCB的值为.
7.如图,已知两点A(2,0),B(0,4),且∠1=∠2,则tan∠OCA=2.
8.如图,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A′处.若EA′的延长线恰好过点C,则sin∠ABE的值为.
9.将一副三角板按如图的方式摆放在一起,连接AD,则tan∠ADB=.
10.如图,在△ABC中,∠ACB=90°,BC=6,AC=8,已知点D在边BA的延长线上,AB=2AD,则tan∠DCA=.
三、解答题
11.如图所示,在直角坐标平面内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.求:
(1)点B的坐标;
(2)cos∠BAO的值.
解:(1)过点B作BH⊥OA于点H,
在Rt△OHB中,∵BO=5,
sin∠BOA=,
∴BH=3.∴OH==4.
∴点B的坐标为(4,3).
(2)∵OA=10,OH=4,∴AH=6.
在Rt△AHB中,∵BH=3,
∴AB==3.
∴cos∠BAO==.
12.如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等.若等腰直角△ABC的三个顶点分别在这三条平行直线上,斜边AC与l3所夹的锐角为α,求tanα的值.
解:过点A作l1的垂线,垂足为D,过点C作l1,l3的垂线,垂足为E,F,
设l1,l2之间的距离为a,
则l2与l3之间的距离也为a.
∵∠ABC=90°,∴∠DBA+∠EBC=90°.
∵∠DBA+∠DAB=90°,∴∠EBC=∠DAB.
又∵∠ADB=∠BEC,AB=BC,
∴△ADB≌△BEC(AAS).
∴AD=BE=2a,DB=EC=a.
∴AF=DE=3a.
∴tanα===.
13.如图,点E在正方形ABCD的边AB上,连接DE,过点C作CF⊥DE于点F,过点A作AG∥CF交DE于点G.
(1)求证:△DCF≌△ADG;
(2)若点E是AB的中点,设∠DCF=α,求sinα的值.
解:(1)证明:在正方形ABCD中,AD=DC,
∠ADC=90°,
∵CF⊥DE,
∴∠CFD=∠CFG=90°.
∵AG∥CF,
∴∠AGD=∠CFG=90°.
∴∠AGD=∠CFD.
∵∠ADG+∠CDE=∠ADC=90°,
∠DCF+∠CDE=90°,
∴∠ADG=∠DCF.
在△DCF和△ADG中,
∴△DCF≌△ADG(AAS).
(2)设正方形ABCD的边长为2a.
∵点E是AB的中点,
∴AE=×2a=a.
在Rt△ADE中,DE===a,
∴sin∠ADG===.
∵∠ADG=∠DCF=α,
∴sinα=.
14.如图,在4×4的网格中,每个小正方形的边长为1,线段AB,CD的端点均为格点.
(1)AB的长度为2,CD的长度为;
(2)若AB与CD所夹锐角为α,求tanα的值.
解:取格点E,连接CE,使CE∥AB,取格点F,连接EF,交CD于点G,取格点H,使CH=2,
∵∠CHD=∠EDF=90°,HD=DF=3,CH=DE=3,
∴△CHD≌△EDF(SAS).
∴∠EDG=∠EFD.
又∵∠GED=∠DEF,∴△DEG∽△FED.
∴==,即==.
∴EG=,DG=.
∴CG=CD-DG=.
∴tan∠ECG==.
∵AB∥CE,∴α=∠ECG.
∴tanα=.
