2020-2021学年北师大版九年级数学下册第一章 1.1.1 正切 同步练习题(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版九年级数学下册第一章 1.1.1 正切 同步练习题(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 117.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 14:51:56 | ||
图片预览


文档简介
2020-2021学年北师大版九年级数学下册第一章
1.1.1
正切
同步练习题
一、选择题
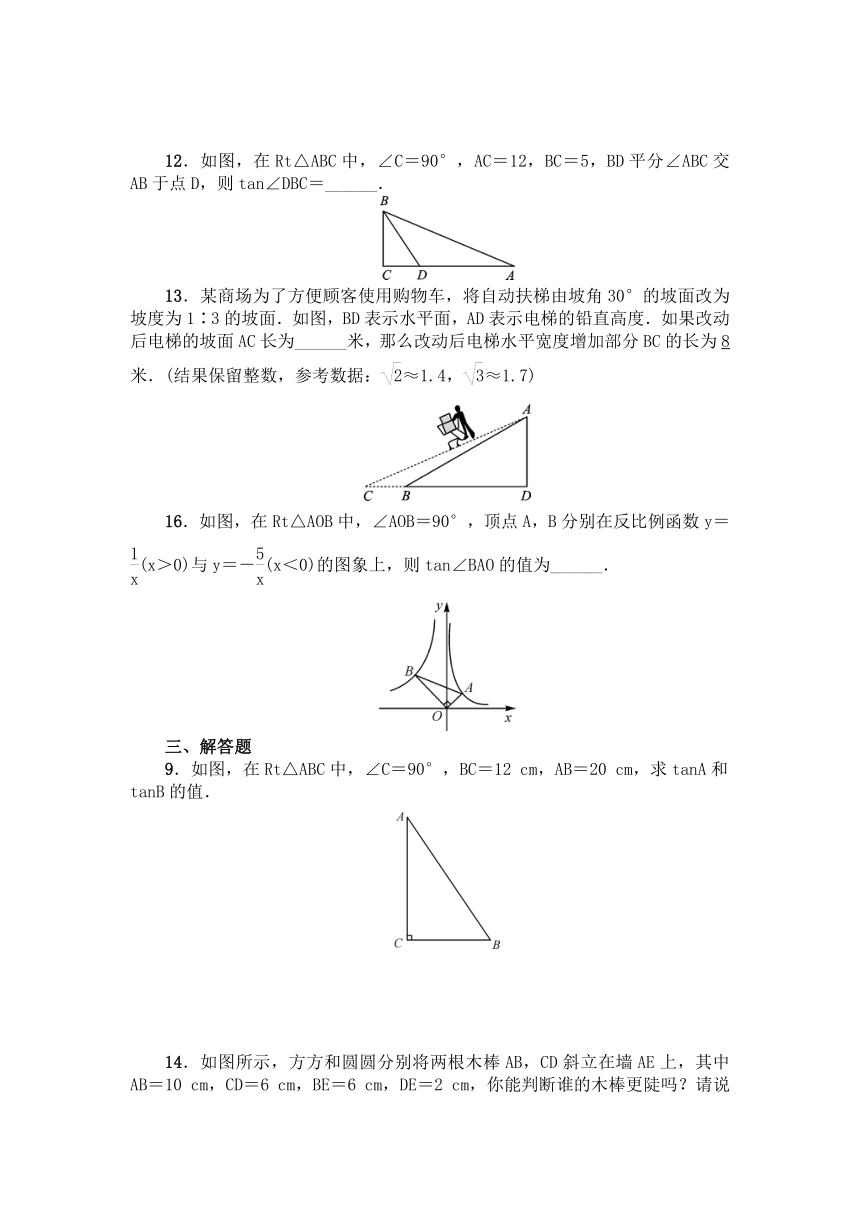
1.如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为(
)
A.2
B.
C.
D.
2.为测量如图所示的上山坡道的倾斜度,小明测得图中所示的数据(单位:米),则该坡道的坡度是(
)
A.
B.4
C.
D.
3.在Rt△ABC中,∠C=90°,若三角形各边同时扩大三倍,则tanA的值(
)
A.扩大为原来的三倍
B.不变
C.缩小为原来的
D.不确定
4.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知AB=6,AC=3,则tan∠BCD的值为(
)
A.
B.
C.
D.
5.如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为(
)
A.
B.
C.2
D.2
二、填空题
6.如图,在Rt△ABC中,∠C=90°,BC=15,tanA=,则AB=______.
7.如图,在Rt△ABD中,∠A=90°,点C在AD上,∠ACB=45°,tanD=,则=______.
8.如图,直线y=2x+4交x轴于点A,交y轴于点B,则tan∠OAB=______.
10.如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE∶EB=4∶1,EF⊥AC于点F,连接FB,则tan∠CFB=______.
11.如图,等腰△ABC的腰AB,AC的长为5,底边长为6,则tanC=______.
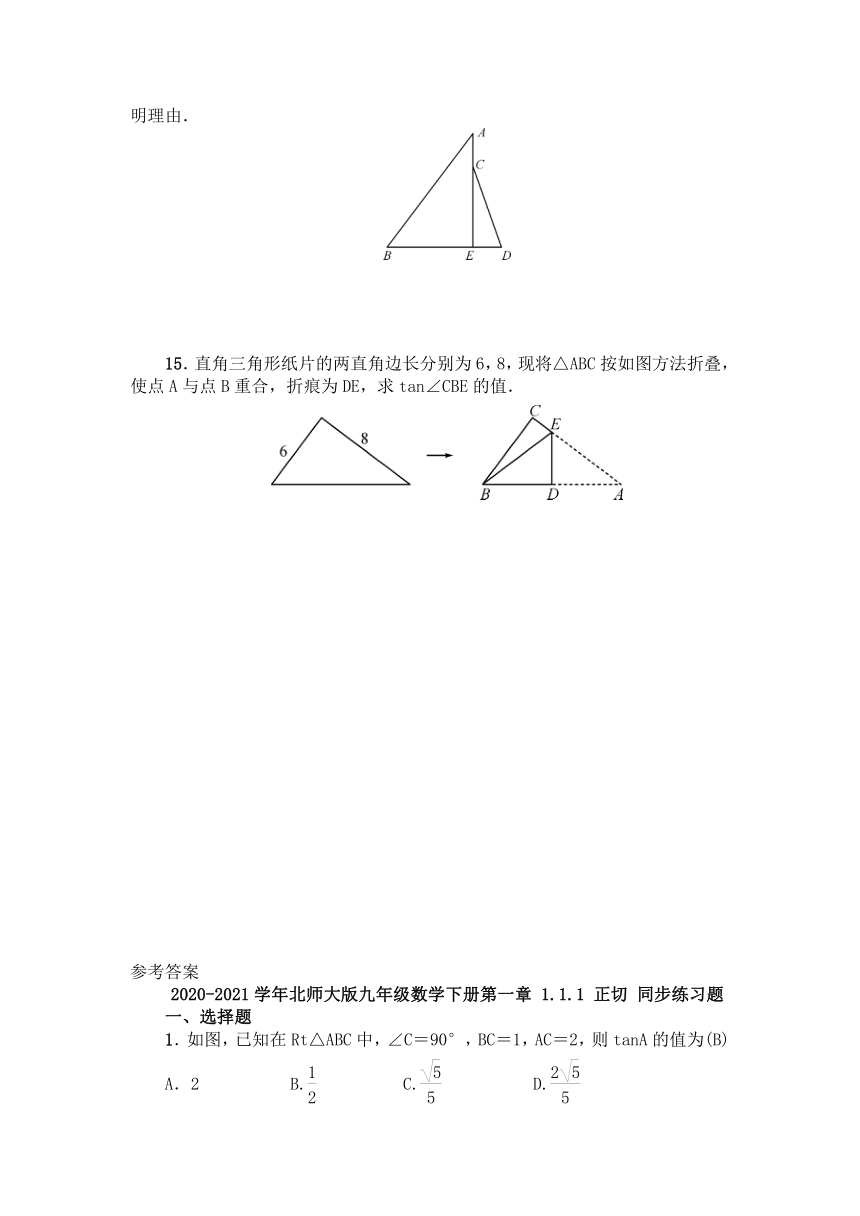
12.如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,BD平分∠ABC交AB于点D,则tan∠DBC=______.
13.某商场为了方便顾客使用购物车,将自动扶梯由坡角30°的坡面改为坡度为1∶3的坡面.如图,BD表示水平面,AD表示电梯的铅直高度.如果改动后电梯的坡面AC长为______米,那么改动后电梯水平宽度增加部分BC的长为8米.(结果保留整数,参考数据:≈1.4,≈1.7)
16.如图,在Rt△AOB中,∠AOB=90°,顶点A,B分别在反比例函数y=(x>0)与y=-(x<0)的图象上,则tan∠BAO的值为______.
三、解答题
9.如图,在Rt△ABC中,∠C=90°,BC=12
cm,AB=20
cm,求tanA和tanB的值.
14.如图所示,方方和圆圆分别将两根木棒AB,CD斜立在墙AE上,其中AB=10
cm,CD=6
cm,BE=6
cm,DE=2
cm,你能判断谁的木棒更陡吗?请说明理由.
15.直角三角形纸片的两直角边长分别为6,8,现将△ABC按如图方法折叠,使点A与点B重合,折痕为DE,求tan∠CBE的值.
参考答案
2020-2021学年北师大版九年级数学下册第一章
1.1.1
正切
同步练习题
一、选择题
1.如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为(B)
A.2
B.
C.
D.
2.为测量如图所示的上山坡道的倾斜度,小明测得图中所示的数据(单位:米),则该坡道的坡度是(A)
A.
B.4
C.
D.
3.在Rt△ABC中,∠C=90°,若三角形各边同时扩大三倍,则tanA的值(B)
A.扩大为原来的三倍
B.不变
C.缩小为原来的
D.不确定
4.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知AB=6,AC=3,则tan∠BCD的值为(A)
A.
B.
C.
D.
5.如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为(A)
A.
B.
C.2
D.2
二、填空题
6.如图,在Rt△ABC中,∠C=90°,BC=15,tanA=,则AB=17.
7.如图,在Rt△ABD中,∠A=90°,点C在AD上,∠ACB=45°,tanD=,则=.
8.如图,直线y=2x+4交x轴于点A,交y轴于点B,则tan∠OAB=2.
10.如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE∶EB=4∶1,EF⊥AC于点F,连接FB,则tan∠CFB=.
11.如图,等腰△ABC的腰AB,AC的长为5,底边长为6,则tanC=.
12.如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,BD平分∠ABC交AB于点D,则tan∠DBC=.
13.某商场为了方便顾客使用购物车,将自动扶梯由坡角30°的坡面改为坡度为1∶3的坡面.如图,BD表示水平面,AD表示电梯的铅直高度.如果改动后电梯的坡面AC长为6米,那么改动后电梯水平宽度增加部分BC的长为8米.(结果保留整数,参考数据:≈1.4,≈1.7)
16.如图,在Rt△AOB中,∠AOB=90°,顶点A,B分别在反比例函数y=(x>0)与y=-(x<0)的图象上,则tan∠BAO的值为.
三、解答题
9.如图,在Rt△ABC中,∠C=90°,BC=12
cm,AB=20
cm,求tanA和tanB的值.
解:∵∠C=90°,BC=12
cm,
AB=20
cm,
∴AC==16
cm.
∴tanA===,
tanB===.
14.如图所示,方方和圆圆分别将两根木棒AB,CD斜立在墙AE上,其中AB=10
cm,CD=6
cm,BE=6
cm,DE=2
cm,你能判断谁的木棒更陡吗?请说明理由.
解:∵AB=10
cm,BE=6
cm,
∴AE==8
cm.
∴斜坡AB的坡度为=.
∵CD=6
cm,DE=2
cm,
∴CE==4
cm.
∴斜坡CD的坡度为==2.
∵<2,
∴圆圆的木棒CD更陡.
15.直角三角形纸片的两直角边长分别为6,8,现将△ABC按如图方法折叠,使点A与点B重合,折痕为DE,求tan∠CBE的值.
解:由折叠性质,得BE=AE.
设CE=x,则BE=AE=8-x.
在Rt△BCE中,根据勾股定理,得
BE2=BC2+CE2,即(8-x)2=62+x2,解得x=.
∴tan∠CBE==.
1.1.1
正切
同步练习题
一、选择题
1.如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为(
)
A.2
B.
C.
D.
2.为测量如图所示的上山坡道的倾斜度,小明测得图中所示的数据(单位:米),则该坡道的坡度是(
)
A.
B.4
C.
D.
3.在Rt△ABC中,∠C=90°,若三角形各边同时扩大三倍,则tanA的值(
)
A.扩大为原来的三倍
B.不变
C.缩小为原来的
D.不确定
4.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知AB=6,AC=3,则tan∠BCD的值为(
)
A.
B.
C.
D.
5.如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为(
)
A.
B.
C.2
D.2
二、填空题
6.如图,在Rt△ABC中,∠C=90°,BC=15,tanA=,则AB=______.
7.如图,在Rt△ABD中,∠A=90°,点C在AD上,∠ACB=45°,tanD=,则=______.
8.如图,直线y=2x+4交x轴于点A,交y轴于点B,则tan∠OAB=______.
10.如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE∶EB=4∶1,EF⊥AC于点F,连接FB,则tan∠CFB=______.
11.如图,等腰△ABC的腰AB,AC的长为5,底边长为6,则tanC=______.
12.如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,BD平分∠ABC交AB于点D,则tan∠DBC=______.
13.某商场为了方便顾客使用购物车,将自动扶梯由坡角30°的坡面改为坡度为1∶3的坡面.如图,BD表示水平面,AD表示电梯的铅直高度.如果改动后电梯的坡面AC长为______米,那么改动后电梯水平宽度增加部分BC的长为8米.(结果保留整数,参考数据:≈1.4,≈1.7)
16.如图,在Rt△AOB中,∠AOB=90°,顶点A,B分别在反比例函数y=(x>0)与y=-(x<0)的图象上,则tan∠BAO的值为______.
三、解答题
9.如图,在Rt△ABC中,∠C=90°,BC=12
cm,AB=20
cm,求tanA和tanB的值.
14.如图所示,方方和圆圆分别将两根木棒AB,CD斜立在墙AE上,其中AB=10
cm,CD=6
cm,BE=6
cm,DE=2
cm,你能判断谁的木棒更陡吗?请说明理由.
15.直角三角形纸片的两直角边长分别为6,8,现将△ABC按如图方法折叠,使点A与点B重合,折痕为DE,求tan∠CBE的值.
参考答案
2020-2021学年北师大版九年级数学下册第一章
1.1.1
正切
同步练习题
一、选择题
1.如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为(B)
A.2
B.
C.
D.
2.为测量如图所示的上山坡道的倾斜度,小明测得图中所示的数据(单位:米),则该坡道的坡度是(A)
A.
B.4
C.
D.
3.在Rt△ABC中,∠C=90°,若三角形各边同时扩大三倍,则tanA的值(B)
A.扩大为原来的三倍
B.不变
C.缩小为原来的
D.不确定
4.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知AB=6,AC=3,则tan∠BCD的值为(A)
A.
B.
C.
D.
5.如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为(A)
A.
B.
C.2
D.2
二、填空题
6.如图,在Rt△ABC中,∠C=90°,BC=15,tanA=,则AB=17.
7.如图,在Rt△ABD中,∠A=90°,点C在AD上,∠ACB=45°,tanD=,则=.
8.如图,直线y=2x+4交x轴于点A,交y轴于点B,则tan∠OAB=2.
10.如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE∶EB=4∶1,EF⊥AC于点F,连接FB,则tan∠CFB=.
11.如图,等腰△ABC的腰AB,AC的长为5,底边长为6,则tanC=.
12.如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,BD平分∠ABC交AB于点D,则tan∠DBC=.
13.某商场为了方便顾客使用购物车,将自动扶梯由坡角30°的坡面改为坡度为1∶3的坡面.如图,BD表示水平面,AD表示电梯的铅直高度.如果改动后电梯的坡面AC长为6米,那么改动后电梯水平宽度增加部分BC的长为8米.(结果保留整数,参考数据:≈1.4,≈1.7)
16.如图,在Rt△AOB中,∠AOB=90°,顶点A,B分别在反比例函数y=(x>0)与y=-(x<0)的图象上,则tan∠BAO的值为.
三、解答题
9.如图,在Rt△ABC中,∠C=90°,BC=12
cm,AB=20
cm,求tanA和tanB的值.
解:∵∠C=90°,BC=12
cm,
AB=20
cm,
∴AC==16
cm.
∴tanA===,
tanB===.
14.如图所示,方方和圆圆分别将两根木棒AB,CD斜立在墙AE上,其中AB=10
cm,CD=6
cm,BE=6
cm,DE=2
cm,你能判断谁的木棒更陡吗?请说明理由.
解:∵AB=10
cm,BE=6
cm,
∴AE==8
cm.
∴斜坡AB的坡度为=.
∵CD=6
cm,DE=2
cm,
∴CE==4
cm.
∴斜坡CD的坡度为==2.
∵<2,
∴圆圆的木棒CD更陡.
15.直角三角形纸片的两直角边长分别为6,8,现将△ABC按如图方法折叠,使点A与点B重合,折痕为DE,求tan∠CBE的值.
解:由折叠性质,得BE=AE.
设CE=x,则BE=AE=8-x.
在Rt△BCE中,根据勾股定理,得
BE2=BC2+CE2,即(8-x)2=62+x2,解得x=.
∴tan∠CBE==.
