2020-2021学年华东师大版数学八年级下册 第16章 分式 章节复习练习题(word版含答案)
文档属性
| 名称 | 2020-2021学年华东师大版数学八年级下册 第16章 分式 章节复习练习题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 46.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 14:49:38 | ||
图片预览


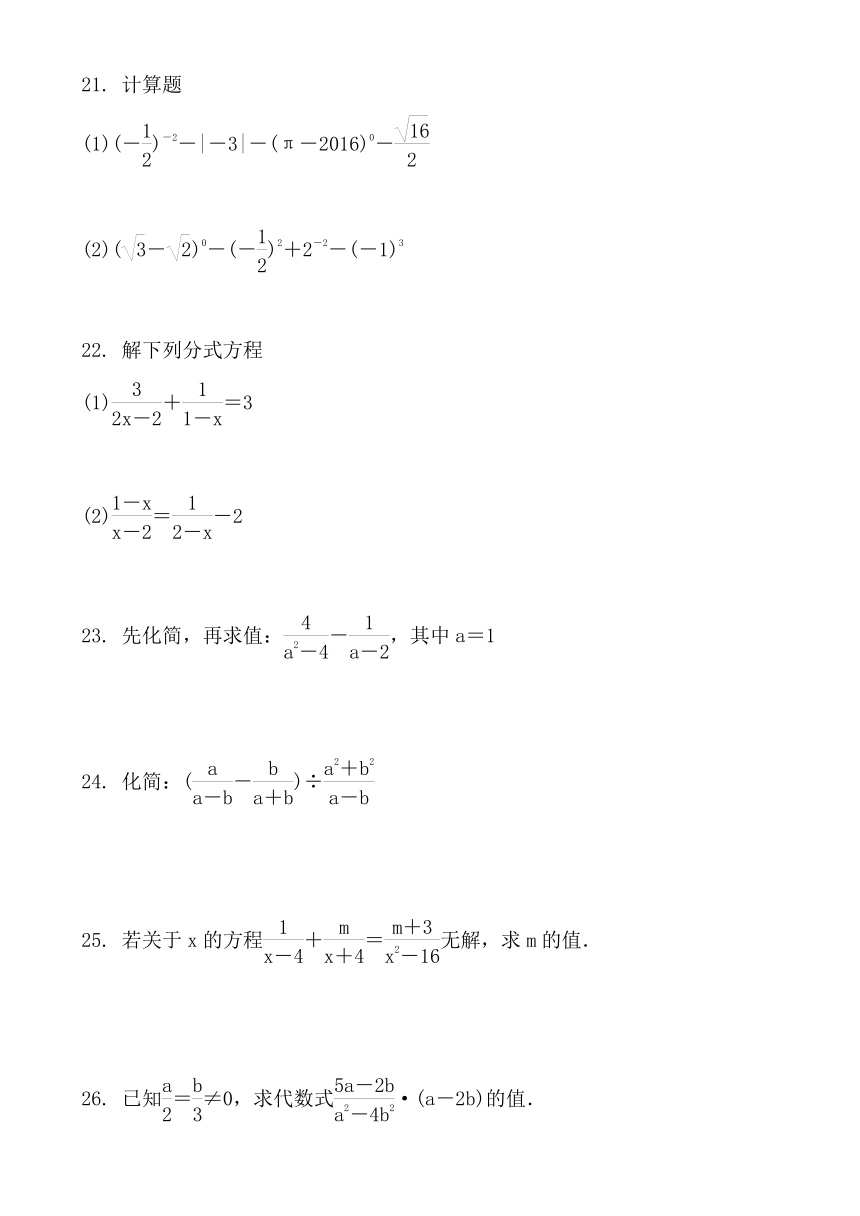

文档简介
第16章 分式
1.下列有理式:,,a+b,,-m2,,其中是分式的有( )
A.2个
B.3个
C.4个
D.5个
2.分式方程=的解是( )
A.x=-2
B.x=1
C.x=2
D.x=3
3.下列分式:,,,,其中是最简分式的有( )
A.1个
B.2个
C.3个
D.4个
4.某种流感病毒的最大直径为0.00000012米,这一直径用科学记数法表示为(
)
A.1.2×10-9米
B.1.2×10-8米
C.12×10-8米
D.1.2×10-7米
5.化简÷的结果是(
)
A.a2
B.
C.
D.
6.把分式方程-=1化为整式方程正确的是(
)
A.2(x+1)-x2=1
B.2(x+1)+x2=1
C.2(x+1)-x2=x(x+1)
D.2x-(x+1)2=x(x+1)
7.下列计算错误的是(
)
A.=
B.=a-b
C.=
D.-=-
8.下列等式成立的是(
)
A.(-3)-2=-9
B.(-3)-2=
C.a-2×b-2=a2×b2
D.=a+b
9.若方程=+有增根,则增根可能为(
)
A.0
B.2
C.0或2
D.1
10.如果a-b=2,那么代数式(-b)·的值为(
)
A.
B.25
C.3
D.4
11.若分式(m-n≠0)的分母经过通分后变为m2-n2,则分子变为
.
12.如果分式的值为-1,则x的值是
.
13.如果a+b=2,那么代数式(a-)÷的值是
.
14.若m+=3,那么m2+=
.
15.对于非零的两个实数a、b,规定a?b=-,
若2?(2x-1)=1,则x的值为
.
16.在()2,()-2,()2,()0四个数中,最小的是
.
17.成都地铁五号线一、二期工程即将开工,该工程投资预算约为3
600
000万元,这一数据用科学记数法表示为
.
18.当x=______时,分式的值与的值互为相反数.
19.不改变分式的值,把分式的分子、分母各项系数化为整数得____________.
20.
杭州到北京的铁路长1487千米,火车的原平均速度为x千米/时,提速后平均速度增加了70千米/时,由杭州到北京的行驶时间缩短了3小时,则可列方程
.
21.
计算题
(1)(-)-2-|-3|-(π-2016)0-
(2)(-)0-(-)2+2-2-(-1)3
22.
解下列分式方程
(1)+=3
(2)=-2
23.
先化简,再求值:-,其中a=1
24.
化简:(-)÷
25.
若关于x的方程+=无解,求m的值.
26.
已知=≠0,求代数式·(a-2b)的值.
27.
某班在“世界读书日”开展了图书交换活动,第一组同学共带图书24本,第二组同学共带图书27本.已知第一组同学比第二组同学平均每人多带1本图书,第二组人数是第一组人数的1.5倍.求第一组的人数.
28.
国家实施高效节能电器的财政补贴政策,某款空调在政策实施后,客户每购买一台可获得补贴500元,若同样用11万元购买此款空调,补贴后可购买的台数比补贴前多20%,则该款空调补贴前的售价为每台多少元?
29.
某校为了进一步开展“阳光体育”活动,购买了一批乒乓球拍和羽毛球拍.已知一副羽毛球拍比一副乒乓球拍贵20元,购买羽毛球拍的费用比购买乒乓球拍的2
000元要多,多出的部分能购买25副乒乓球拍.
(1)若每副乒乓球拍的价格为x元,请你用含x的代数式表示该校购买这批乒乓球拍和羽毛球拍的总费用;
(2)若购买的两种球拍数一样,求x.
30.
某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
答案:
1-10
BDBDD
CBBCA
11.
5m2+5mn
12.
0
13.
a+b
14.
7
15.
16.
()2
17.
3.6×106万元
18.
1
19.
20.
-=3
21.
解:(1)原式=4-3-1-2=-2
(2)原式=1-+-(-1)=2.
22.
(1)
解:3-2=3(2x-2),1=6x-6,x=,
检验:x=代入2(x-1)≠0,
∴x=是原分式方程的解
(2)
解:1-x=-1-2(x-2),-x+2x=-1+4-1,
x=2,检验:x=2使(x-2)=0,
∴x=2是增根舍去,∴原分式方程无解
23.
解:原式=-==-,当a=1时,原式=-
24.
解:原式=×=
25.
解:去分母得:x+4+m(x-4)=m+3,可得(m+1)x=5m-1,当m+1=0时,一元一次方程无解,此时m=-1;当m+1≠0时,则x==±4,解得m=5或-,综上所述:m=-1或5或-
.
26.
解:
原式=,设a=2k,b=3k(k≠0),得原式==
27.
解:设第一组有x人,根据题意,得=+1,解得x=6,
经检验,x=6是原方程的解,且符合题意.答:第一组有6人
28.
解:设该款空调补贴前的售价为每台x元,根据题意得:×(1+20%)=,即=,解得:x=3000,检验:把x=3000代入x(x-500)中x(x-500)≠0,因此x=3000是原方程的根,且符合题意.
29.
解:(1)4
000+25x(元)
(2)设购买每副乒乓球拍用去了x元,则购买每副羽毛球拍用去了(x+20)元.由题意得=,解得x1=40,x2=-40,经检验,x1,x2都是原方程的根.但x>0,∴x=40.即每副乒乓球拍为40元
30.
解:(1)设甲种树苗每棵的价格是x元,则乙种树苗每棵的价格是(x+10)元,依题意有=,解得x=30.经检验,x=30是原方程的解,
x+10=30+10=40.
答:甲种树苗每棵的价格是30元,乙种树苗每棵的价格是40元;
(2)设他们可购买y棵乙种树苗,依题意有30×(1-10%)(50-y)+40y≤1500,解得y≤11,∵y为整数,∴y最大为11.
答:他们最多可购买11棵乙种树苗.
1.下列有理式:,,a+b,,-m2,,其中是分式的有( )
A.2个
B.3个
C.4个
D.5个
2.分式方程=的解是( )
A.x=-2
B.x=1
C.x=2
D.x=3
3.下列分式:,,,,其中是最简分式的有( )
A.1个
B.2个
C.3个
D.4个
4.某种流感病毒的最大直径为0.00000012米,这一直径用科学记数法表示为(
)
A.1.2×10-9米
B.1.2×10-8米
C.12×10-8米
D.1.2×10-7米
5.化简÷的结果是(
)
A.a2
B.
C.
D.
6.把分式方程-=1化为整式方程正确的是(
)
A.2(x+1)-x2=1
B.2(x+1)+x2=1
C.2(x+1)-x2=x(x+1)
D.2x-(x+1)2=x(x+1)
7.下列计算错误的是(
)
A.=
B.=a-b
C.=
D.-=-
8.下列等式成立的是(
)
A.(-3)-2=-9
B.(-3)-2=
C.a-2×b-2=a2×b2
D.=a+b
9.若方程=+有增根,则增根可能为(
)
A.0
B.2
C.0或2
D.1
10.如果a-b=2,那么代数式(-b)·的值为(
)
A.
B.25
C.3
D.4
11.若分式(m-n≠0)的分母经过通分后变为m2-n2,则分子变为
.
12.如果分式的值为-1,则x的值是
.
13.如果a+b=2,那么代数式(a-)÷的值是
.
14.若m+=3,那么m2+=
.
15.对于非零的两个实数a、b,规定a?b=-,
若2?(2x-1)=1,则x的值为
.
16.在()2,()-2,()2,()0四个数中,最小的是
.
17.成都地铁五号线一、二期工程即将开工,该工程投资预算约为3
600
000万元,这一数据用科学记数法表示为
.
18.当x=______时,分式的值与的值互为相反数.
19.不改变分式的值,把分式的分子、分母各项系数化为整数得____________.
20.
杭州到北京的铁路长1487千米,火车的原平均速度为x千米/时,提速后平均速度增加了70千米/时,由杭州到北京的行驶时间缩短了3小时,则可列方程
.
21.
计算题
(1)(-)-2-|-3|-(π-2016)0-
(2)(-)0-(-)2+2-2-(-1)3
22.
解下列分式方程
(1)+=3
(2)=-2
23.
先化简,再求值:-,其中a=1
24.
化简:(-)÷
25.
若关于x的方程+=无解,求m的值.
26.
已知=≠0,求代数式·(a-2b)的值.
27.
某班在“世界读书日”开展了图书交换活动,第一组同学共带图书24本,第二组同学共带图书27本.已知第一组同学比第二组同学平均每人多带1本图书,第二组人数是第一组人数的1.5倍.求第一组的人数.
28.
国家实施高效节能电器的财政补贴政策,某款空调在政策实施后,客户每购买一台可获得补贴500元,若同样用11万元购买此款空调,补贴后可购买的台数比补贴前多20%,则该款空调补贴前的售价为每台多少元?
29.
某校为了进一步开展“阳光体育”活动,购买了一批乒乓球拍和羽毛球拍.已知一副羽毛球拍比一副乒乓球拍贵20元,购买羽毛球拍的费用比购买乒乓球拍的2
000元要多,多出的部分能购买25副乒乓球拍.
(1)若每副乒乓球拍的价格为x元,请你用含x的代数式表示该校购买这批乒乓球拍和羽毛球拍的总费用;
(2)若购买的两种球拍数一样,求x.
30.
某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
答案:
1-10
BDBDD
CBBCA
11.
5m2+5mn
12.
0
13.
a+b
14.
7
15.
16.
()2
17.
3.6×106万元
18.
1
19.
20.
-=3
21.
解:(1)原式=4-3-1-2=-2
(2)原式=1-+-(-1)=2.
22.
(1)
解:3-2=3(2x-2),1=6x-6,x=,
检验:x=代入2(x-1)≠0,
∴x=是原分式方程的解
(2)
解:1-x=-1-2(x-2),-x+2x=-1+4-1,
x=2,检验:x=2使(x-2)=0,
∴x=2是增根舍去,∴原分式方程无解
23.
解:原式=-==-,当a=1时,原式=-
24.
解:原式=×=
25.
解:去分母得:x+4+m(x-4)=m+3,可得(m+1)x=5m-1,当m+1=0时,一元一次方程无解,此时m=-1;当m+1≠0时,则x==±4,解得m=5或-,综上所述:m=-1或5或-
.
26.
解:
原式=,设a=2k,b=3k(k≠0),得原式==
27.
解:设第一组有x人,根据题意,得=+1,解得x=6,
经检验,x=6是原方程的解,且符合题意.答:第一组有6人
28.
解:设该款空调补贴前的售价为每台x元,根据题意得:×(1+20%)=,即=,解得:x=3000,检验:把x=3000代入x(x-500)中x(x-500)≠0,因此x=3000是原方程的根,且符合题意.
29.
解:(1)4
000+25x(元)
(2)设购买每副乒乓球拍用去了x元,则购买每副羽毛球拍用去了(x+20)元.由题意得=,解得x1=40,x2=-40,经检验,x1,x2都是原方程的根.但x>0,∴x=40.即每副乒乓球拍为40元
30.
解:(1)设甲种树苗每棵的价格是x元,则乙种树苗每棵的价格是(x+10)元,依题意有=,解得x=30.经检验,x=30是原方程的解,
x+10=30+10=40.
答:甲种树苗每棵的价格是30元,乙种树苗每棵的价格是40元;
(2)设他们可购买y棵乙种树苗,依题意有30×(1-10%)(50-y)+40y≤1500,解得y≤11,∵y为整数,∴y最大为11.
答:他们最多可购买11棵乙种树苗.
