学考专题复习必修4(1)任意角的三角函数和诱导公式
文档属性
| 名称 | 学考专题复习必修4(1)任意角的三角函数和诱导公式 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
知识点一 任意角
1.任意角
2.象限角
使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么,角的终边在第几象限,就说这个角是第几象限角;如果角的终边在坐标轴上,那么这个角不属于任何一个象限.
3.终边相同的角
所有与角α终边相同的角,连同角α在内,构成的角的集合是S={β|β=k·360°+α,k∈Z}.
特别提醒:一些特殊角的集合表示:
(1)终边在x轴上的角的集合:{β|β=k·180°,k∈Z}.
(2)终边在y轴上的角的集合:{β|β=k·180°+90°,k∈Z}.
知识点二 弧度制
1.定义
把长度等于半径长的弧所对的圆心角叫做1弧度的角,正角的弧度数是正数,负角的弧度数是负数,零角的弧度数是0.
2.角度制和弧度制的互化
180°=π
rad,1°=
rad,1
rad=°.
3.扇形的弧长及面积公式
弧长公式:l=|α|·r,
面积公式:S=lr=|α|·r2,
其中r为扇形的半径.
知识点三 任意角的三角函数与同角三角函数的基本关系
1.任意角α的终边与单位圆交于点P(x,y)时,sin
α=y,cos
α=x,tan
α=(x≠0).三个三角函数的初步性质如下表:
三角函数
定义域
第一象限符号
第二象限符号
第三象限符号
第四象限符号
sin
α
R
+
+
-
-
cos
α
R
+
-
-
+
tan
α
+
-
+
-
2.同角三角函数的基本关系
(1)平方关系:sin2α+cos2α=1.
(2)商数关系:=tan
α.
特别提醒:平方关系,一般为隐含条件,可直接应用,注意“1”的代换.
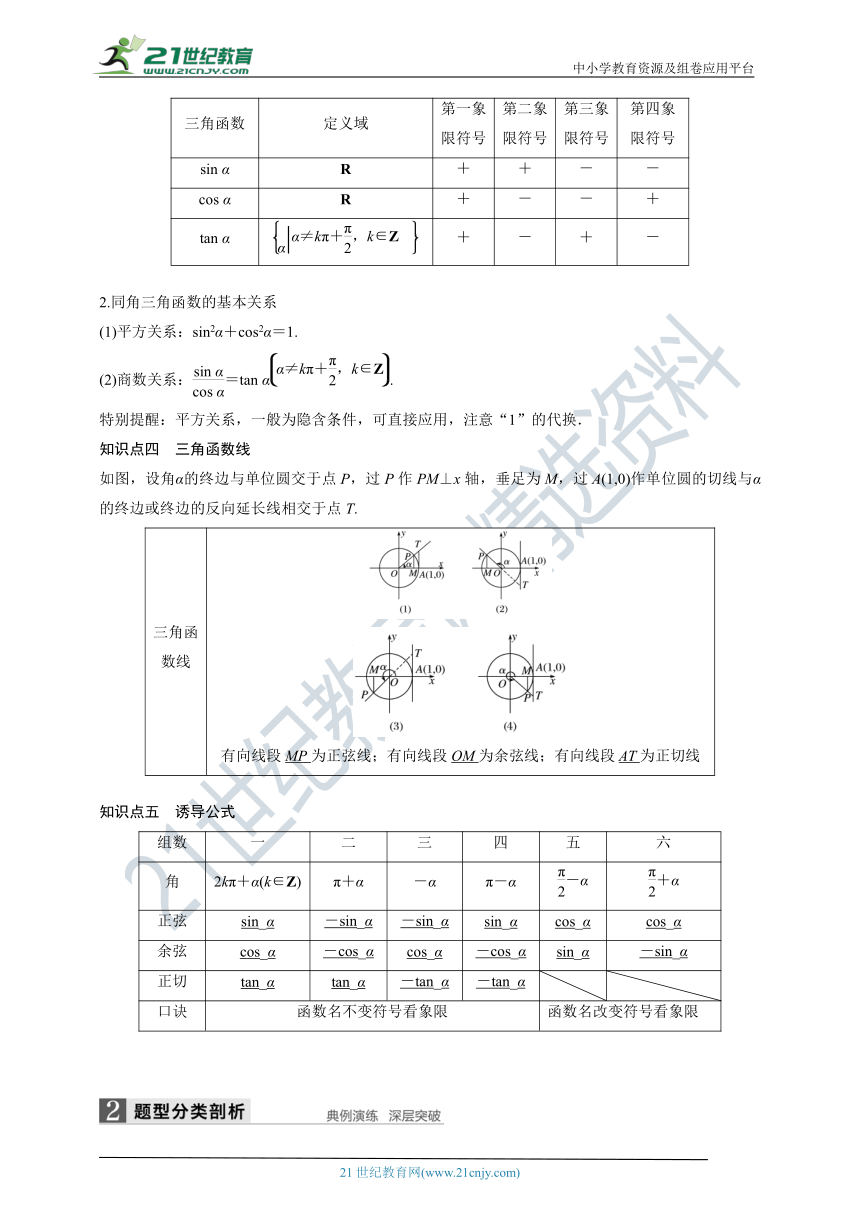
知识点四 三角函数线
如图,设角α的终边与单位圆交于点P,过P作PM⊥x轴,垂足为M,过A(1,0)作单位圆的切线与α的终边或终边的反向延长线相交于点T.
三角函数线
有向线段MP为正弦线;有向线段OM为余弦线;有向线段AT为正切线
知识点五 诱导公式
组数
一
二
三
四
五
六
角
2kπ+α(k∈Z)
π+α
-α
π-α
-α
+α
正弦
sin_α
-sin_α
-sin_α
sin_α
cos_α
cos_α
余弦
cos_α
-cos_α
cos_α
-cos_α
sin_α
-sin_α
正切
tan_α
tan_α
-tan_α
-tan_α
口诀
函数名不变符号看象限
函数名改变符号看象限
题型一 弧度制扇形的弧长、面积公式的应用
例1 已知一扇形的圆心角为α(α>0),所在圆的半径为R.
(1)若α=60°,R=10
cm,求扇形的弧长及该弧所在的弓形的面积;
(2)若扇形的周长是一定值C(C>0),当α(α>0)为多少弧度时,该扇形有最大面积?
解 (1)设弧长为l,弓形面积为S弓,
则α=60°=,R=10
cm,l=×10=(cm),
S弓=S扇-S△=××10-×102×sin
=π-=50(cm2).
(2)扇形周长C=2R+l=2R+αR,
∴R=,∴S扇=αR2=α2
=·=·≤.
当且仅当α2=4,即α=2时,
扇形面积有最大值.
感悟与点拨 涉及弧长和扇形面积的计算时,可用的公式有角度表示和弧度表示两种,其中弧度表示的公式结构简单,易记好用,在使用前,应将圆心角用弧度表示.弧长和扇形面积公式:l=|α|R,S=|α|R2.
跟踪训练1 (1)设扇形的周长为8
cm,面积为4
cm2,则扇形的圆心角的弧度数为( )
A.2
B.4
C.1
D.
(2)已知扇形的周长为4
cm,当它的半径为________cm和圆心角为________弧度时,扇形面积最大,这个最大面积是________cm2.
答案 (1)A (2)1 2 1
解析 (1)设扇形弧长为l,半径为r,
则解得∴α==2.
(2)设扇形的圆心角为α,半径为r,
则2r+|α|r=4,∴|α|=-2.
∴S扇形=|α|·r2=2r-r2=-(r-1)2+1,
∵r>0,∴当r=1时,(S扇形)max=1,此时|α|=2.
题型二 角的概念及其表示
例2 已知角α=,在区间[-4π,0]内与角α有相同终边的角β=________.
答案 -或-
解析 由终边相同的角关系知β=k·2π+,k∈Z,
∴取k=-2,-1,得β=-或β=-.
感悟与点拨 (1)利用终边相同的角的集合可以求适合某些条件的角,方法是先写出与这个角的终边相同的所有角的集合,然后通过对集合中的参数k赋值来求得所需角.
(2)利用终边相同的角的集合S={β|β=2kπ+α,k∈Z}判断一个角β所在象限时,只需把这个角写成[0,2π)范围内的一个角α与2π的整数倍的和,然后判断角α的象限.
跟踪训练2 (1)若角α的终边在直线y=-x上,则角α的取值集合为( )
A.
B.
C.
D.
(2)α=k·180°+45°(k∈Z),则α在( )
A.第一或第三象限
B.第一或第二象限
C.第二或第四象限
D.第三或第四象限
答案 (1)D (2)A
题型三 三角函数的定义及符号法则
例3 已知角α的终边过点P(-8m,-6sin
30°),且cos
α=-,则实数m的值为( )
A.
B.±
C.-
D.
答案 A
解析 点P(-8m,-6sin
30°),即P(-8m,-3),
所以cos
α=,即=-,
解得m2=.
又cos
α=-<0,所以m>0,所以m=,故选A.
感悟与点拨 (1)已知角α终边上的点P(x,y),先算|OP|=,若|OP|=1,则sin
α=y,cos
α=x,tan
α=(x≠0),若|OP|≠1,则sin
α=,cos
α=,tan
α=(x≠0).
(2)三角函数的符号法则是由三角函数定义推导出来的,掌握定义,熟记法则.
跟踪训练3 (1)已知角θ的顶点与原点重合,始边与x轴的非负半轴重合,终边在直线y=2x上,则cos
2θ的值为( )
A.-
B.-
C.
D.
(2)若点P(sin
θcos
θ,cos
θ)位于第二象限,则角θ所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案 (1)B (2)D
解析 (1)设P(a,2a)(a≠0)是角θ终边上的任一点,
则|OP|=a或|OP|=-a,
∴cos
θ==±,
∴cos
2θ=2cos2θ-1=-1=-.
(2)∵点P位于第二象限,
∴即
故θ角的终边位于第四象限.
题型四 同角三角函数关系
例4 已知tan
α=2.
(1)求的值;
(2)求的值.
解 (1)方法一 由tan
α=2,得α为第一象限角或第三象限角.
由得
当α为第一象限角时,sin
α=,cos
α=;
当α为第三象限角时,sin
α=-,cos
α=-.
代入原式,得原式=-1.
方法二 (化“切”为“弦”)
由tan
α=2,得sin
α=2cos
α.
原式===-1.
方法三 (化“弦”为“切”)
把原式的分子、分母同除以cos
α,
得==-1.
(2)=
===.
感悟与点拨 (1)利用sin2α+cos2α=1可以实现角α的正弦、余弦的互化,利用=tan
α可以实现角α的弦切互化.
(2)应用公式时注意方程思想的应用:对于sin
α+cos
α,sin
α·cos
α,sin
α-cos
α这三个式子,利用(sin
α±cos
α)2=1±2sin
αcos
α,可以知一求二.
(3)注意公式逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α.
跟踪训练4 (1)若tan
θ=,则cos
2θ等于( )
A.-
B.-
C.
D.
(2)已知-x+cos
x=,则sin
x-cos
x的值为________
答案 (1)D (2)-
解析 (1)cos
2θ=====.
(2)∵(sin
x-cos
x)2+(sin
x+cos
x)2=2,
∴|sin
x-cos
x|=.
∵-x<0,cos
x>0,
∴sin
x-cos
x<0,∴sin
x-cos
x=-.
题型五 诱导公式的应用
例5 (1)已知cos=,求cos的值;
(2)已知π<α<2π,cos(α-7π)=-,求sin(3π+α)·tan的值.
解 (1)∵+=π,
∴-α=π-.
∴cos=cos
=-cos=-,
即cos=-.
(2)∵cos(α-7π)=cos(7π-α)=cos(π-α)
=-cos
α=-,
∴cos
α=.
∴sin(3π+α)·tan
=sin(π+α)·
=sin
α·tan
=sin
α·
=sin
α·=cos
α=.
感悟与点拨 熟练运用诱导公式和基本关系式,并确定相应三角函数值的符号是解题的关键.另外,注意(1)弦切互化;(2)整体的观点,如:可以把“+α”看作一个整体.
跟踪训练5 (1)已知sin=,则cos的值为________.
(2)已知sin
α是方程5x2-7x-6=0的根,α是第三象限角,则·tan2(π-α)=______.
答案 (1)- (2)-
解析 (1)cos=cos
=-sin=-.
(2)∵方程5x2-7x-6=0的根为-或2,
又α是第三象限角,∴sin
α=-,
∴cos
α=-=-,
∴tan
α===,
∴原式=·tan2α=-tan2α=-.
一、选择题
1.已知扇形的半径为12
cm,弧长为18
cm,则扇形圆心角的弧度数是( )
A.
B.
C.
D.
答案 B
解析 α===.
2.已知角θ的终边上有一点P(-4a,3a)(a≠0),则2sin
θ+cos
θ的值为( )
A.
B.-
C.或-
D.不确定
答案 C
解析 由r==5|a|,
当a>0时,r=5a,
则2sin
θ+cos
θ=2×+=;
当a<0时,r=-5a,
则2sin
θ+cos
θ=2×+=-,
∴2sin
θ+cos
θ=±.
3.(2018年4月学考)若锐角α满足sin=,则sin
α等于( )
A.
B.
C.
D.
答案 D
4.若=,则tan
θ等于( )
A.1
B.-1
C.3
D.-3
答案 D
解析 ∵=
==,
∴tan
θ=-3.
5.若角α和角β的终边关于x轴对称,则角α可以用角β表示为( )
A.2kπ+β(k∈Z)
B.2kπ-β(k∈Z)
C.kπ+β(k∈Z)
D.kπ-β(k∈Z)
答案 B
解析 ∵角α与角β的终边关于x轴对称,
∴α=-β+2kπ,k∈Z.
6.已知tan
θ=2,则sin2θ+sin
θcos
θ-2cos2θ等于( )
A.-
B.
C.-
D.
答案 D
解析 ∵tan
θ=2,∴sin2θ+sin
θcos
θ-2cos2θ
=
==.
7.设tan(π+α)=2,则等于( )
A.3
B.
C.1
D.-1
答案 A
解析 由tan(π+α)=2,得tan
α=2,
则=
===3.
8.已知cos
α-sin
α=-,则sin
αcos
α等于( )
A.
B.±
C.
D.±
答案 A
解析 ∵cos
α-sin
α=-,
两边平方可得1-2sin
αcos
α=,
∴sin
αcos
α=.
9.cos+sin的值为( )
A.-
B.
C.
D.
答案 C
解析 cos+sin=cos
π+sin
π
=-+=.
10.已知cos(π+α)=-,则sin的值为( )
A.
B.-
C.
D.-
答案 D
解析 ∵cos(π+α)=-cos
α=-,
∴cos
α=,∴sin=-sin=-cos
α=-.
二、填空题
11.如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为,则cos
α=_________.
答案 -
解析 因为A点纵坐标yA=,且A点在第二象限,
又因为圆O为单位圆,所以A点横坐标xA=-,
由三角函数的定义可得cos
α=-.
12.在△ABC中,sin
A=,则角A=________.
答案
解析 由sin
A=,
两边平方得2sin2A=3cos
A,
∵sin2A=1-cos2A,∴2cos2A+3cos
A-2=0,
解得cos
A=或cos
A=-2(舍去),
∵013.已知角θ的顶点在坐标原点,始边与x轴非负半轴重合,终边在直线2x-y=0上,则=________.
答案 2
解析 由题意可得tan
θ=2,
原式===2.
14.已知sin
θ=,则=________.
答案
解析 ====.
三、解答题
15.已知f(α)=.
(1)化简f(α);
(2)若α是第三象限角,且cos=,求f(α)的值.
解 (1)根据已知的关系式,结合诱导公式可知,
f(α)=
==-cos
α.
(2)∵α是第三象限角,且cos=cos
=-cos=-sin
α=,
∴sin
α=-,cos
α=-,
∴f(α)=-cos
α=.
16.在△ABC中,若sin(2π+A)=-sin(2π-B),cos
A=-cos(π-B),求△ABC的三个内角.
解 由已知得化简得2cos2A=1,即cos
A=±.
(1)当cos
A=时,cos
B=,
又A,B是三角形的内角,∴A=,B=,C=.
(2)当cos
A=-时,cos
B=-,
又A,B是三角形的内角,
∴A=,B=,不合题意.
综上可知,A=,B=,C=.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
知识点一 任意角
1.任意角
2.象限角
使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么,角的终边在第几象限,就说这个角是第几象限角;如果角的终边在坐标轴上,那么这个角不属于任何一个象限.
3.终边相同的角
所有与角α终边相同的角,连同角α在内,构成的角的集合是S={β|β=k·360°+α,k∈Z}.
特别提醒:一些特殊角的集合表示:
(1)终边在x轴上的角的集合:{β|β=k·180°,k∈Z}.
(2)终边在y轴上的角的集合:{β|β=k·180°+90°,k∈Z}.
知识点二 弧度制
1.定义
把长度等于半径长的弧所对的圆心角叫做1弧度的角,正角的弧度数是正数,负角的弧度数是负数,零角的弧度数是0.
2.角度制和弧度制的互化
180°=π
rad,1°=
rad,1
rad=°.
3.扇形的弧长及面积公式
弧长公式:l=|α|·r,
面积公式:S=lr=|α|·r2,
其中r为扇形的半径.
知识点三 任意角的三角函数与同角三角函数的基本关系
1.任意角α的终边与单位圆交于点P(x,y)时,sin
α=y,cos
α=x,tan
α=(x≠0).三个三角函数的初步性质如下表:
三角函数
定义域
第一象限符号
第二象限符号
第三象限符号
第四象限符号
sin
α
R
+
+
-
-
cos
α
R
+
-
-
+
tan
α
+
-
+
-
2.同角三角函数的基本关系
(1)平方关系:sin2α+cos2α=1.
(2)商数关系:=tan
α.
特别提醒:平方关系,一般为隐含条件,可直接应用,注意“1”的代换.
知识点四 三角函数线
如图,设角α的终边与单位圆交于点P,过P作PM⊥x轴,垂足为M,过A(1,0)作单位圆的切线与α的终边或终边的反向延长线相交于点T.
三角函数线
有向线段MP为正弦线;有向线段OM为余弦线;有向线段AT为正切线
知识点五 诱导公式
组数
一
二
三
四
五
六
角
2kπ+α(k∈Z)
π+α
-α
π-α
-α
+α
正弦
sin_α
-sin_α
-sin_α
sin_α
cos_α
cos_α
余弦
cos_α
-cos_α
cos_α
-cos_α
sin_α
-sin_α
正切
tan_α
tan_α
-tan_α
-tan_α
口诀
函数名不变符号看象限
函数名改变符号看象限
题型一 弧度制扇形的弧长、面积公式的应用
例1 已知一扇形的圆心角为α(α>0),所在圆的半径为R.
(1)若α=60°,R=10
cm,求扇形的弧长及该弧所在的弓形的面积;
(2)若扇形的周长是一定值C(C>0),当α(α>0)为多少弧度时,该扇形有最大面积?
解 (1)设弧长为l,弓形面积为S弓,
则α=60°=,R=10
cm,l=×10=(cm),
S弓=S扇-S△=××10-×102×sin
=π-=50(cm2).
(2)扇形周长C=2R+l=2R+αR,
∴R=,∴S扇=αR2=α2
=·=·≤.
当且仅当α2=4,即α=2时,
扇形面积有最大值.
感悟与点拨 涉及弧长和扇形面积的计算时,可用的公式有角度表示和弧度表示两种,其中弧度表示的公式结构简单,易记好用,在使用前,应将圆心角用弧度表示.弧长和扇形面积公式:l=|α|R,S=|α|R2.
跟踪训练1 (1)设扇形的周长为8
cm,面积为4
cm2,则扇形的圆心角的弧度数为( )
A.2
B.4
C.1
D.
(2)已知扇形的周长为4
cm,当它的半径为________cm和圆心角为________弧度时,扇形面积最大,这个最大面积是________cm2.
答案 (1)A (2)1 2 1
解析 (1)设扇形弧长为l,半径为r,
则解得∴α==2.
(2)设扇形的圆心角为α,半径为r,
则2r+|α|r=4,∴|α|=-2.
∴S扇形=|α|·r2=2r-r2=-(r-1)2+1,
∵r>0,∴当r=1时,(S扇形)max=1,此时|α|=2.
题型二 角的概念及其表示
例2 已知角α=,在区间[-4π,0]内与角α有相同终边的角β=________.
答案 -或-
解析 由终边相同的角关系知β=k·2π+,k∈Z,
∴取k=-2,-1,得β=-或β=-.
感悟与点拨 (1)利用终边相同的角的集合可以求适合某些条件的角,方法是先写出与这个角的终边相同的所有角的集合,然后通过对集合中的参数k赋值来求得所需角.
(2)利用终边相同的角的集合S={β|β=2kπ+α,k∈Z}判断一个角β所在象限时,只需把这个角写成[0,2π)范围内的一个角α与2π的整数倍的和,然后判断角α的象限.
跟踪训练2 (1)若角α的终边在直线y=-x上,则角α的取值集合为( )
A.
B.
C.
D.
(2)α=k·180°+45°(k∈Z),则α在( )
A.第一或第三象限
B.第一或第二象限
C.第二或第四象限
D.第三或第四象限
答案 (1)D (2)A
题型三 三角函数的定义及符号法则
例3 已知角α的终边过点P(-8m,-6sin
30°),且cos
α=-,则实数m的值为( )
A.
B.±
C.-
D.
答案 A
解析 点P(-8m,-6sin
30°),即P(-8m,-3),
所以cos
α=,即=-,
解得m2=.
又cos
α=-<0,所以m>0,所以m=,故选A.
感悟与点拨 (1)已知角α终边上的点P(x,y),先算|OP|=,若|OP|=1,则sin
α=y,cos
α=x,tan
α=(x≠0),若|OP|≠1,则sin
α=,cos
α=,tan
α=(x≠0).
(2)三角函数的符号法则是由三角函数定义推导出来的,掌握定义,熟记法则.
跟踪训练3 (1)已知角θ的顶点与原点重合,始边与x轴的非负半轴重合,终边在直线y=2x上,则cos
2θ的值为( )
A.-
B.-
C.
D.
(2)若点P(sin
θcos
θ,cos
θ)位于第二象限,则角θ所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案 (1)B (2)D
解析 (1)设P(a,2a)(a≠0)是角θ终边上的任一点,
则|OP|=a或|OP|=-a,
∴cos
θ==±,
∴cos
2θ=2cos2θ-1=-1=-.
(2)∵点P位于第二象限,
∴即
故θ角的终边位于第四象限.
题型四 同角三角函数关系
例4 已知tan
α=2.
(1)求的值;
(2)求的值.
解 (1)方法一 由tan
α=2,得α为第一象限角或第三象限角.
由得
当α为第一象限角时,sin
α=,cos
α=;
当α为第三象限角时,sin
α=-,cos
α=-.
代入原式,得原式=-1.
方法二 (化“切”为“弦”)
由tan
α=2,得sin
α=2cos
α.
原式===-1.
方法三 (化“弦”为“切”)
把原式的分子、分母同除以cos
α,
得==-1.
(2)=
===.
感悟与点拨 (1)利用sin2α+cos2α=1可以实现角α的正弦、余弦的互化,利用=tan
α可以实现角α的弦切互化.
(2)应用公式时注意方程思想的应用:对于sin
α+cos
α,sin
α·cos
α,sin
α-cos
α这三个式子,利用(sin
α±cos
α)2=1±2sin
αcos
α,可以知一求二.
(3)注意公式逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α.
跟踪训练4 (1)若tan
θ=,则cos
2θ等于( )
A.-
B.-
C.
D.
(2)已知-
x=,则sin
x-cos
x的值为________
答案 (1)D (2)-
解析 (1)cos
2θ=====.
(2)∵(sin
x-cos
x)2+(sin
x+cos
x)2=2,
∴|sin
x-cos
x|=.
∵-
x>0,
∴sin
x-cos
x<0,∴sin
x-cos
x=-.
题型五 诱导公式的应用
例5 (1)已知cos=,求cos的值;
(2)已知π<α<2π,cos(α-7π)=-,求sin(3π+α)·tan的值.
解 (1)∵+=π,
∴-α=π-.
∴cos=cos
=-cos=-,
即cos=-.
(2)∵cos(α-7π)=cos(7π-α)=cos(π-α)
=-cos
α=-,
∴cos
α=.
∴sin(3π+α)·tan
=sin(π+α)·
=sin
α·tan
=sin
α·
=sin
α·=cos
α=.
感悟与点拨 熟练运用诱导公式和基本关系式,并确定相应三角函数值的符号是解题的关键.另外,注意(1)弦切互化;(2)整体的观点,如:可以把“+α”看作一个整体.
跟踪训练5 (1)已知sin=,则cos的值为________.
(2)已知sin
α是方程5x2-7x-6=0的根,α是第三象限角,则·tan2(π-α)=______.
答案 (1)- (2)-
解析 (1)cos=cos
=-sin=-.
(2)∵方程5x2-7x-6=0的根为-或2,
又α是第三象限角,∴sin
α=-,
∴cos
α=-=-,
∴tan
α===,
∴原式=·tan2α=-tan2α=-.
一、选择题
1.已知扇形的半径为12
cm,弧长为18
cm,则扇形圆心角的弧度数是( )
A.
B.
C.
D.
答案 B
解析 α===.
2.已知角θ的终边上有一点P(-4a,3a)(a≠0),则2sin
θ+cos
θ的值为( )
A.
B.-
C.或-
D.不确定
答案 C
解析 由r==5|a|,
当a>0时,r=5a,
则2sin
θ+cos
θ=2×+=;
当a<0时,r=-5a,
则2sin
θ+cos
θ=2×+=-,
∴2sin
θ+cos
θ=±.
3.(2018年4月学考)若锐角α满足sin=,则sin
α等于( )
A.
B.
C.
D.
答案 D
4.若=,则tan
θ等于( )
A.1
B.-1
C.3
D.-3
答案 D
解析 ∵=
==,
∴tan
θ=-3.
5.若角α和角β的终边关于x轴对称,则角α可以用角β表示为( )
A.2kπ+β(k∈Z)
B.2kπ-β(k∈Z)
C.kπ+β(k∈Z)
D.kπ-β(k∈Z)
答案 B
解析 ∵角α与角β的终边关于x轴对称,
∴α=-β+2kπ,k∈Z.
6.已知tan
θ=2,则sin2θ+sin
θcos
θ-2cos2θ等于( )
A.-
B.
C.-
D.
答案 D
解析 ∵tan
θ=2,∴sin2θ+sin
θcos
θ-2cos2θ
=
==.
7.设tan(π+α)=2,则等于( )
A.3
B.
C.1
D.-1
答案 A
解析 由tan(π+α)=2,得tan
α=2,
则=
===3.
8.已知cos
α-sin
α=-,则sin
αcos
α等于( )
A.
B.±
C.
D.±
答案 A
解析 ∵cos
α-sin
α=-,
两边平方可得1-2sin
αcos
α=,
∴sin
αcos
α=.
9.cos+sin的值为( )
A.-
B.
C.
D.
答案 C
解析 cos+sin=cos
π+sin
π
=-+=.
10.已知cos(π+α)=-,则sin的值为( )
A.
B.-
C.
D.-
答案 D
解析 ∵cos(π+α)=-cos
α=-,
∴cos
α=,∴sin=-sin=-cos
α=-.
二、填空题
11.如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为,则cos
α=_________.
答案 -
解析 因为A点纵坐标yA=,且A点在第二象限,
又因为圆O为单位圆,所以A点横坐标xA=-,
由三角函数的定义可得cos
α=-.
12.在△ABC中,sin
A=,则角A=________.
答案
解析 由sin
A=,
两边平方得2sin2A=3cos
A,
∵sin2A=1-cos2A,∴2cos2A+3cos
A-2=0,
解得cos
A=或cos
A=-2(舍去),
∵0
答案 2
解析 由题意可得tan
θ=2,
原式===2.
14.已知sin
θ=,则=________.
答案
解析 ====.
三、解答题
15.已知f(α)=.
(1)化简f(α);
(2)若α是第三象限角,且cos=,求f(α)的值.
解 (1)根据已知的关系式,结合诱导公式可知,
f(α)=
==-cos
α.
(2)∵α是第三象限角,且cos=cos
=-cos=-sin
α=,
∴sin
α=-,cos
α=-,
∴f(α)=-cos
α=.
16.在△ABC中,若sin(2π+A)=-sin(2π-B),cos
A=-cos(π-B),求△ABC的三个内角.
解 由已知得化简得2cos2A=1,即cos
A=±.
(1)当cos
A=时,cos
B=,
又A,B是三角形的内角,∴A=,B=,C=.
(2)当cos
A=-时,cos
B=-,
又A,B是三角形的内角,
∴A=,B=,不合题意.
综上可知,A=,B=,C=.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
