17.1.3 利用勾股定理表示无理数课件(18张)
文档属性
| 名称 | 17.1.3 利用勾股定理表示无理数课件(18张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 354.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 13:36:24 | ||
图片预览




文档简介
17.1.3 利用勾股定理表示无理数
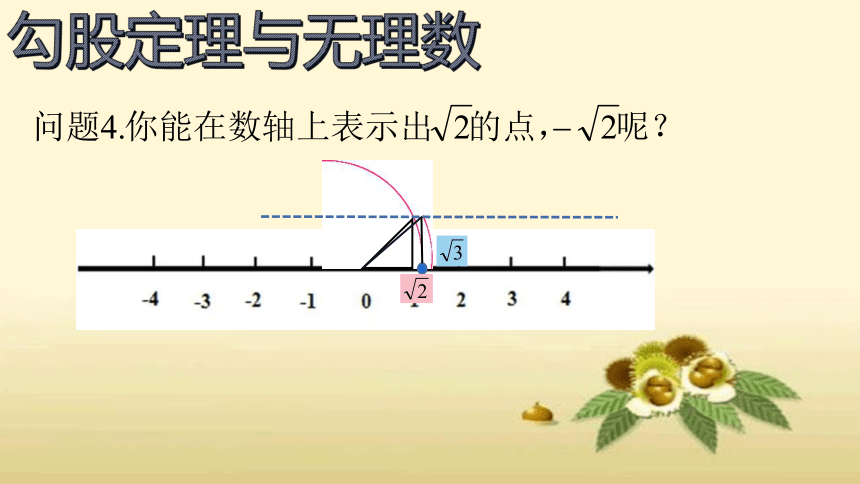
问题1 我们知道数轴上的点与实数一一对应,有的表示有理数,有的表示无理数.你能在数轴上分别画出表示3,-1.5的点吗?
复习引入
复习引入
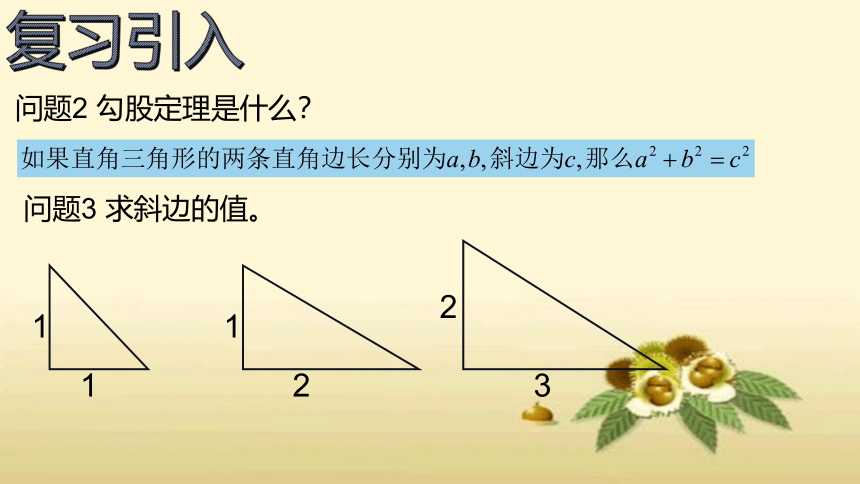
问题2 勾股定理是什么?
问题3 求斜边的值。
1
1
2
1
3
2
勾股定理与无理数
方法:在数轴上画出直角三角形
勾股定理与无理数
勾股定理与无理数
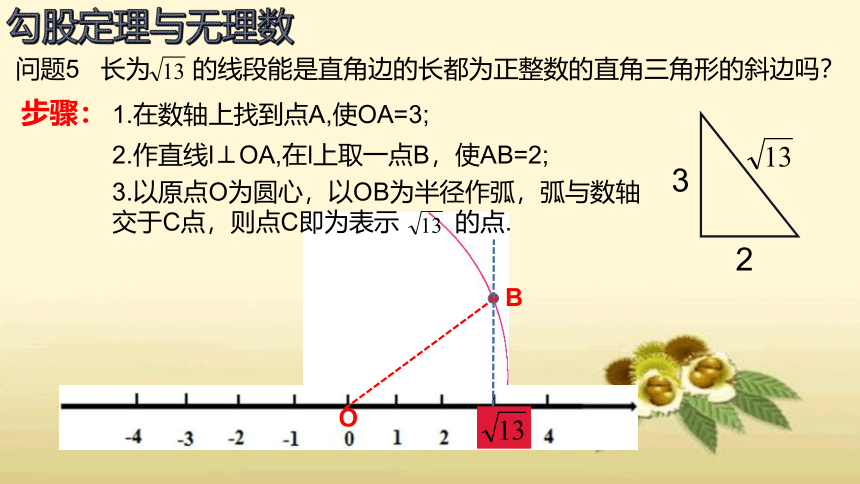
问题5 长为 的线段能是直角边的长都为正整数的直角三角形的斜边吗?
勾股定理与无理数
问题5 长为 的线段能是直角边的长都为正整数的直角三角形的斜边吗?
3
2
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
步骤:
3.以原点O为圆心,以OB为半径作弧,弧与数轴
交于C点,则点C即为表示 的点.
O
A
B
练习
1.如图,在数轴上的点A表示的数是0,点B表示的数是3,CB⊥AB于点B,且BC=2,以点A为圆心,AC为半径画弧交数轴于点D,则点D表示的数是
3. 如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,
则线段AB的长度为( )
A.5 B.6 C.7 D.25
A
4. 如图,在正方形网格中,每个小正方形的边长为1,则网格上的三角形
ABC中,边长为无理数的边数有( )
A.0 B.1 C.2 D.3
D
5. 如图,平面直角坐标系中,点A,B的坐标为分别为(-6,0),(0,8),
以点A为圆心,AB为半径画弧,交 轴的正半轴于点C,求点C的坐标。
∟
D
7.求下列直角三角形的边长
8.求下列直角三角形的边长
D
10.如图,在长方形纸片ABCD中,已知AD=8,
折叠纸片使AB边与对角线AC重合,点B落在点
F处,折痕为AE,且EF=3,则AB=
6
11.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在D′处,求重叠部分三角形AFC 的面积
解:易证△AFD′≌△CFB,
∴D′F=BF,
设D′F=x,则AF=8-x,
在Rt△AFD′中,(8-x)?=x?+4?,
解得x=3.
∴AF=AB-FB=8-3=5,
∴S△AFC=?AF?BC=10.
问题1 我们知道数轴上的点与实数一一对应,有的表示有理数,有的表示无理数.你能在数轴上分别画出表示3,-1.5的点吗?
复习引入
复习引入
问题2 勾股定理是什么?
问题3 求斜边的值。
1
1
2
1
3
2
勾股定理与无理数
方法:在数轴上画出直角三角形
勾股定理与无理数
勾股定理与无理数
问题5 长为 的线段能是直角边的长都为正整数的直角三角形的斜边吗?
勾股定理与无理数
问题5 长为 的线段能是直角边的长都为正整数的直角三角形的斜边吗?
3
2
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
步骤:
3.以原点O为圆心,以OB为半径作弧,弧与数轴
交于C点,则点C即为表示 的点.
O
A
B
练习
1.如图,在数轴上的点A表示的数是0,点B表示的数是3,CB⊥AB于点B,且BC=2,以点A为圆心,AC为半径画弧交数轴于点D,则点D表示的数是
3. 如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,
则线段AB的长度为( )
A.5 B.6 C.7 D.25
A
4. 如图,在正方形网格中,每个小正方形的边长为1,则网格上的三角形
ABC中,边长为无理数的边数有( )
A.0 B.1 C.2 D.3
D
5. 如图,平面直角坐标系中,点A,B的坐标为分别为(-6,0),(0,8),
以点A为圆心,AB为半径画弧,交 轴的正半轴于点C,求点C的坐标。
∟
D
7.求下列直角三角形的边长
8.求下列直角三角形的边长
D
10.如图,在长方形纸片ABCD中,已知AD=8,
折叠纸片使AB边与对角线AC重合,点B落在点
F处,折痕为AE,且EF=3,则AB=
6
11.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在D′处,求重叠部分三角形AFC 的面积
解:易证△AFD′≌△CFB,
∴D′F=BF,
设D′F=x,则AF=8-x,
在Rt△AFD′中,(8-x)?=x?+4?,
解得x=3.
∴AF=AB-FB=8-3=5,
∴S△AFC=?AF?BC=10.
