17.2.2 勾股定理的逆定理的应用课件(16张)
文档属性
| 名称 | 17.2.2 勾股定理的逆定理的应用课件(16张) |  | |
| 格式 | pptx | ||
| 文件大小 | 253.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 13:38:57 | ||
图片预览




文档简介
17.2.2 勾股定理的逆定理的应用
1.勾股定理
如果直角三角形两直角边长分别为a,b,
斜边长为c,那么a?+b?=c?.
复习回顾
2.勾股定理的逆定理
如果三角形ABC的三边长a,b,c满足a?+b?=c?,
那么这个三角形是直角三角形.
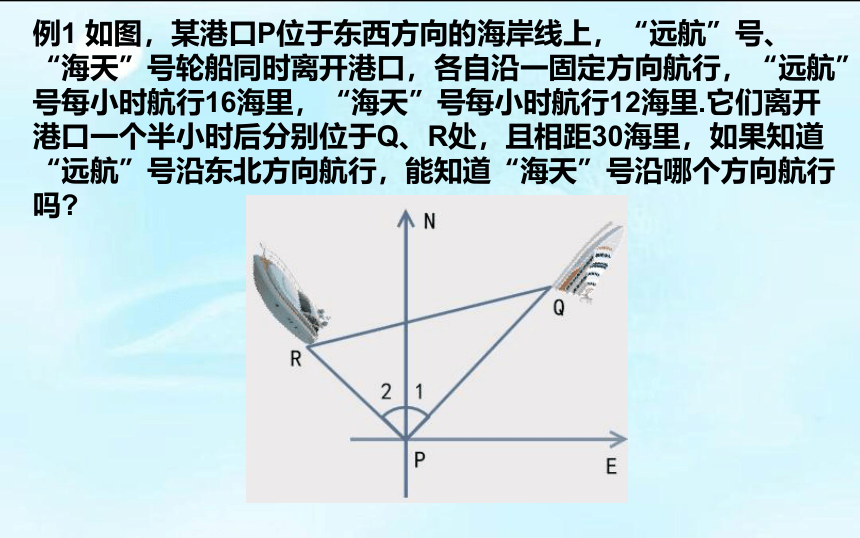
例1 如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于Q、R处,且相距30海里,如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
例2 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔
P的距离为30海里的A处,轮船沿正南方向航行一段时间后
,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船
所在位置B处与灯塔P之间的距离为( )
D
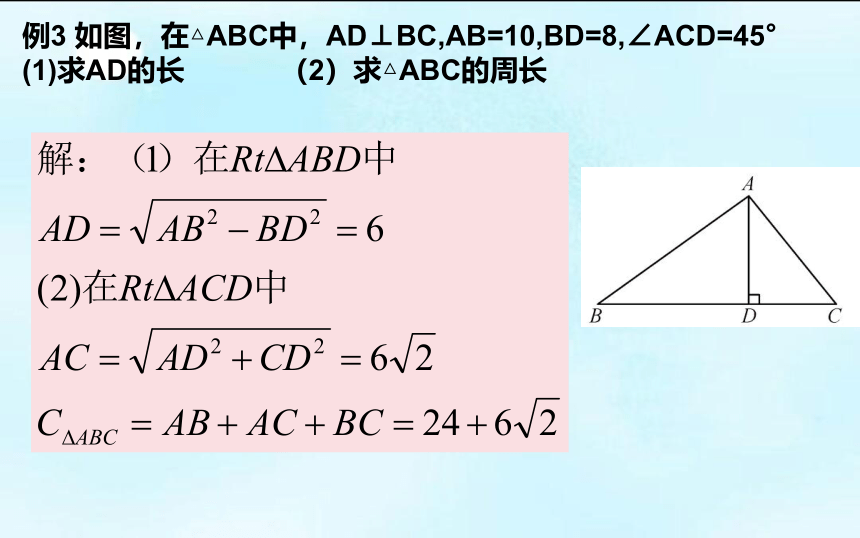
例3 如图,在△ABC中,AD⊥BC,AB=10,BD=8,∠ACD=45°
(1)求AD的长 (2)求△ABC的周长
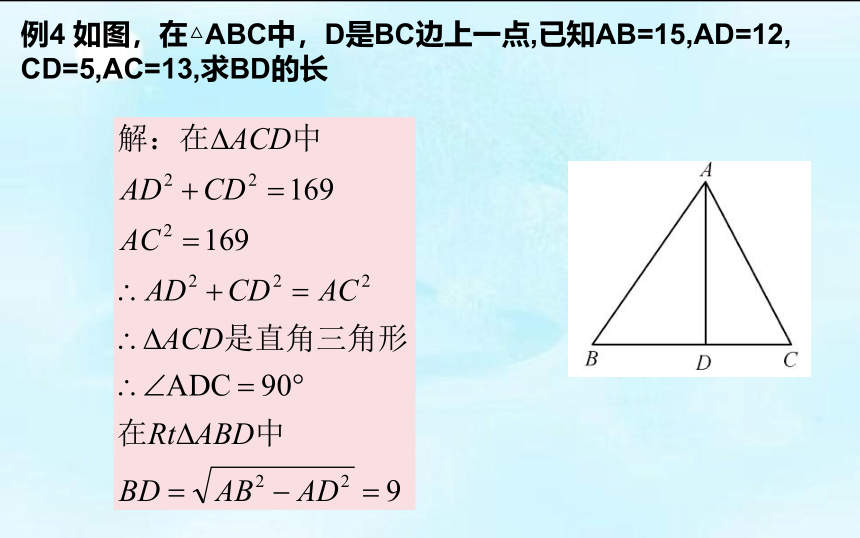
例4 如图,在△ABC中,D是BC边上一点,已知AB=15,AD=12,
CD=5,AC=13,求BD的长
例5 如图,在四边形ABCD中,已知AB=5,BC=3,CD=6,
AD= .若AC⊥BC,求证:AD∥BC.
∴AD∥BC
如果三角形的三边长a,b,c满足a?+b?=c?,那么这个三角形是直角三角形.
满足a?+b?=c?的三个正整数,称为勾股数.
勾股数
常见的勾股数
勾股数拓展性质:
一组勾股数,都扩大相同
倍数k,得到一组新数,这
组数同样是勾股数.
1.下列各组数是勾股数是( )
A.6,8,10 B.7,8,9
C.0.3,0.4,0.5 D.5?,12?,13?
2.下列各组数是勾股数是( )
A.3,4,7 B.1,3,5
C.1.5,2,2.5 D.5,12,13
A
D
解:因为a+b=4,ab=1,
所以a?+b?=(a+b)?-2ab=16-2=14.
又因为c?=14,
所以a?+b?=c?,
所以△ABC是直角三角形.
例6.若△ABC的三边a,b,c,且a+b=4,ab=1,
c= ,试说明△ABC是直角三角形.
在△ABC中,a:b:c=9:15:12,试判断△ABC是直角三角形.
解:依题意,设 a=9k,b=15k,c=12k(k>0),
∵ a?+c?=(9k)?+(12k)?=225k?,
b?=(15k)?=225k?,
∴ a?+b?=c?,
∴ △ABC是直角三角形.
在△ABC中,已知AB=5,AC=12,BC=13,求△ABC的面积
已知:如图,四边形ABCD中,∠B=90°,
AB=3,BC=4,CD=12,AD=13,则四
边形ABCD的面积是
5
36
5.已知△ABC,AB=n?-1,BC=2n,AC=n?+1(n为大于1的正整数).试问△ABC是直角三角形吗?若是,哪一条边所对的角是直角?请说明理由.
解:∵AB?+BC?=(n?-1)?+(2n)?
=n4 -2n?+1+4n?
=n4 +2n?+1
=(n?+1)?
=AC?,
∴△ABC是直角三角形,边AC所对的角是直角.
1.勾股定理
如果直角三角形两直角边长分别为a,b,
斜边长为c,那么a?+b?=c?.
复习回顾
2.勾股定理的逆定理
如果三角形ABC的三边长a,b,c满足a?+b?=c?,
那么这个三角形是直角三角形.
例1 如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于Q、R处,且相距30海里,如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
例2 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔
P的距离为30海里的A处,轮船沿正南方向航行一段时间后
,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船
所在位置B处与灯塔P之间的距离为( )
D
例3 如图,在△ABC中,AD⊥BC,AB=10,BD=8,∠ACD=45°
(1)求AD的长 (2)求△ABC的周长
例4 如图,在△ABC中,D是BC边上一点,已知AB=15,AD=12,
CD=5,AC=13,求BD的长
例5 如图,在四边形ABCD中,已知AB=5,BC=3,CD=6,
AD= .若AC⊥BC,求证:AD∥BC.
∴AD∥BC
如果三角形的三边长a,b,c满足a?+b?=c?,那么这个三角形是直角三角形.
满足a?+b?=c?的三个正整数,称为勾股数.
勾股数
常见的勾股数
勾股数拓展性质:
一组勾股数,都扩大相同
倍数k,得到一组新数,这
组数同样是勾股数.
1.下列各组数是勾股数是( )
A.6,8,10 B.7,8,9
C.0.3,0.4,0.5 D.5?,12?,13?
2.下列各组数是勾股数是( )
A.3,4,7 B.1,3,5
C.1.5,2,2.5 D.5,12,13
A
D
解:因为a+b=4,ab=1,
所以a?+b?=(a+b)?-2ab=16-2=14.
又因为c?=14,
所以a?+b?=c?,
所以△ABC是直角三角形.
例6.若△ABC的三边a,b,c,且a+b=4,ab=1,
c= ,试说明△ABC是直角三角形.
在△ABC中,a:b:c=9:15:12,试判断△ABC是直角三角形.
解:依题意,设 a=9k,b=15k,c=12k(k>0),
∵ a?+c?=(9k)?+(12k)?=225k?,
b?=(15k)?=225k?,
∴ a?+b?=c?,
∴ △ABC是直角三角形.
在△ABC中,已知AB=5,AC=12,BC=13,求△ABC的面积
已知:如图,四边形ABCD中,∠B=90°,
AB=3,BC=4,CD=12,AD=13,则四
边形ABCD的面积是
5
36
5.已知△ABC,AB=n?-1,BC=2n,AC=n?+1(n为大于1的正整数).试问△ABC是直角三角形吗?若是,哪一条边所对的角是直角?请说明理由.
解:∵AB?+BC?=(n?-1)?+(2n)?
=n4 -2n?+1+4n?
=n4 +2n?+1
=(n?+1)?
=AC?,
∴△ABC是直角三角形,边AC所对的角是直角.
