17.2.1 勾股定理的逆定理课件(20张)
文档属性
| 名称 | 17.2.1 勾股定理的逆定理课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 602.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 00:00:00 | ||
图片预览







文档简介
17.2.1 勾股定理的逆定理
温故知新
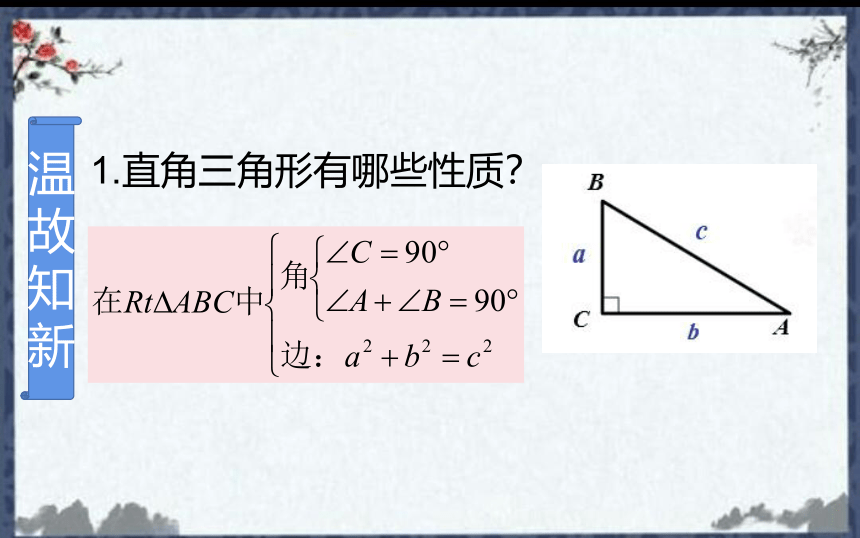
1.直角三角形有哪些性质?
温故知新
2.如何判断三角形是直角三角形?
在△ABC中
(1)∠C=90°
(2)∠A+∠B=90°
答案就藏在课本中,我们一起来看一看!
情境引入
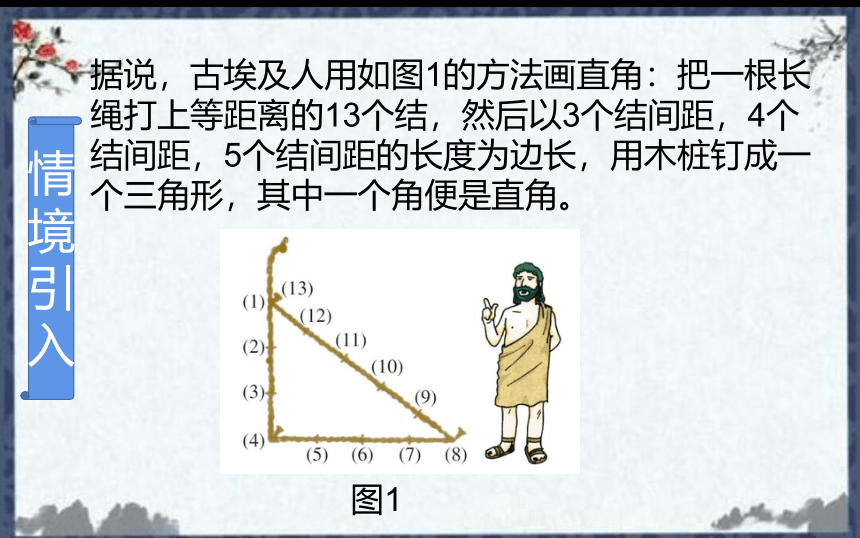
据说,古埃及人用如图1的方法画直角:把一根长
绳打上等距离的13个结,然后以3个结间距,4个
结间距,5个结间距的长度为边长,用木桩钉成一
个三角形,其中一个角便是直角。
图1
如果围成的三角形的三边长分别为3,4,5
3
4
5
探索新知
画一画:下列各组数中的两数平方和等于第三数的平方,分别以这些数为边长画出三角形(单位:cm).
① 2.5,6,6.5;
② 4,7.5,8.5.
探索新知
① 2.5,6,6.5; ② 4,7.5,8.5.
用量角器量一量,它们是什么三角形?
直角三角形
由前面几个例子,我们可以作出什么猜想?
如果三角形ABC的三边长a,b,c满足a?+b?=c?,那么这个三角形是直角三角形.
命题1 如果直角三角形两直角边长分别为a,b,斜边长为c,那么a?+b?=c?.
命题2 如果三角形ABC的三边长a,b,c满足a?+b?=c?,那么这个三角形是直角三角形.
这两个命题有什么不同?
题设
结论
题设
结论
题设和结论相反
我们把像这样,题设和结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题.
探索新知
巩固新知
说出下列命题的逆命题.这些逆命题成立吗?
(1)同旁内角互补,两直线平行
(2)如果两个角是直角,那么它们相等
两直线平行,同旁内角互补。成立
如果两个角相等,那么它们是直角。不成立
巩固新知
说出下列命题的逆命题.这些逆命题成立吗?
(3)全等三角形的对应边相等
(4)如果两个实数相等,那么它们的平方相等
对应边相等的三角形是全等三角形。成立
如果两个实数的平方相等,那么它们相等。不成立
探索新知
命题2 如果三角形ABC的三边长a,b,c满足a?+b?=c?,那么这个三角形是直角三角形.
是否成立呢?如何证明?
已知:如图,△ABC的三边长a,b,c,
满足a?+b?=c?. 求证:△ABC是直角三角形.
证明:画一个△A'B'C',使
∠ C'=90°,B'C'=a,C'A'=b.
∵ ∠ C'=90°,
∴ A'B'2= a?+b?=c?,
∴ A'B' =c.
在△ABC和△A'B'C'中
BC=a=B'C',CA=b=C'A',AB=c=A'B'.
∴ △ ABC ≌△ A'B'C'(SSS).
∴ ∠C=∠C'=90°.
探索新知
勾股定理的逆定理
如果三角形ABC的三边长a,b,c满足a?+b?=c?,那么这个三角形是直角三角形.
巩固新知
判断下列三角形是不是直角三角形
巩固新知
判断下列三角形是不是直角三角形
巩固新知
巩固新知
巩固新知
总结
判断三角形是直角三角形的方法:
在△ABC中
(1)∠C=90°
(2)∠A+∠B=90°
温故知新
1.直角三角形有哪些性质?
温故知新
2.如何判断三角形是直角三角形?
在△ABC中
(1)∠C=90°
(2)∠A+∠B=90°
答案就藏在课本中,我们一起来看一看!
情境引入
据说,古埃及人用如图1的方法画直角:把一根长
绳打上等距离的13个结,然后以3个结间距,4个
结间距,5个结间距的长度为边长,用木桩钉成一
个三角形,其中一个角便是直角。
图1
如果围成的三角形的三边长分别为3,4,5
3
4
5
探索新知
画一画:下列各组数中的两数平方和等于第三数的平方,分别以这些数为边长画出三角形(单位:cm).
① 2.5,6,6.5;
② 4,7.5,8.5.
探索新知
① 2.5,6,6.5; ② 4,7.5,8.5.
用量角器量一量,它们是什么三角形?
直角三角形
由前面几个例子,我们可以作出什么猜想?
如果三角形ABC的三边长a,b,c满足a?+b?=c?,那么这个三角形是直角三角形.
命题1 如果直角三角形两直角边长分别为a,b,斜边长为c,那么a?+b?=c?.
命题2 如果三角形ABC的三边长a,b,c满足a?+b?=c?,那么这个三角形是直角三角形.
这两个命题有什么不同?
题设
结论
题设
结论
题设和结论相反
我们把像这样,题设和结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题.
探索新知
巩固新知
说出下列命题的逆命题.这些逆命题成立吗?
(1)同旁内角互补,两直线平行
(2)如果两个角是直角,那么它们相等
两直线平行,同旁内角互补。成立
如果两个角相等,那么它们是直角。不成立
巩固新知
说出下列命题的逆命题.这些逆命题成立吗?
(3)全等三角形的对应边相等
(4)如果两个实数相等,那么它们的平方相等
对应边相等的三角形是全等三角形。成立
如果两个实数的平方相等,那么它们相等。不成立
探索新知
命题2 如果三角形ABC的三边长a,b,c满足a?+b?=c?,那么这个三角形是直角三角形.
是否成立呢?如何证明?
已知:如图,△ABC的三边长a,b,c,
满足a?+b?=c?. 求证:△ABC是直角三角形.
证明:画一个△A'B'C',使
∠ C'=90°,B'C'=a,C'A'=b.
∵ ∠ C'=90°,
∴ A'B'2= a?+b?=c?,
∴ A'B' =c.
在△ABC和△A'B'C'中
BC=a=B'C',CA=b=C'A',AB=c=A'B'.
∴ △ ABC ≌△ A'B'C'(SSS).
∴ ∠C=∠C'=90°.
探索新知
勾股定理的逆定理
如果三角形ABC的三边长a,b,c满足a?+b?=c?,那么这个三角形是直角三角形.
巩固新知
判断下列三角形是不是直角三角形
巩固新知
判断下列三角形是不是直角三角形
巩固新知
巩固新知
巩固新知
总结
判断三角形是直角三角形的方法:
在△ABC中
(1)∠C=90°
(2)∠A+∠B=90°
