19.1 多边形内角和(第2课时) 正多边形及四边形的不稳定性 课件(共18张PPT)
文档属性
| 名称 | 19.1 多边形内角和(第2课时) 正多边形及四边形的不稳定性 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第
2
课时
正多边形及四边形的不稳定性
沪科版·八年级数学下册
上课课件
第19章
四边形
学习目标
【知识与技能】
1.认识多边形,理解多边形的相关概念
2.掌握多边形的内角和与外角和公式,进一步了解转化的数学思想
3.会用多边形的内角和公式求多边形的内角和并会逆用公式求多边形的边数.
【过程与方法】
1.让学生经历猜想、探索、推理、归纳等过程,发展学生的合情推理能力和语言表达能力,掌握复杂问题化为简单问题,化未知为已知的思想方法.
2.通过把多边形转化为三角形,体会转化思想在几何中的运用,让学生体会从特殊到一般的认识问题的方法.
3.通过探索多边形的内角和与外角和,让学生尝试从不同的角度寻求解决问题的方法,并能有效地解决问题.
【情感与态度】
通过学生间交流、探索,进一步激发学生的学习热情,求知欲望,养成良好的数学思维品质.
【教学重点】
探索多边形的内角和及外角和公式
【教学难点】
如何把多边形转化成三角形,用分割多边形法推导多边形的内角和与外角和.
新课导入
多边形内角和定理:n
边形的内角和等于_________(n
为不小于
3
的整数)
(n-2)·180°
新课推进
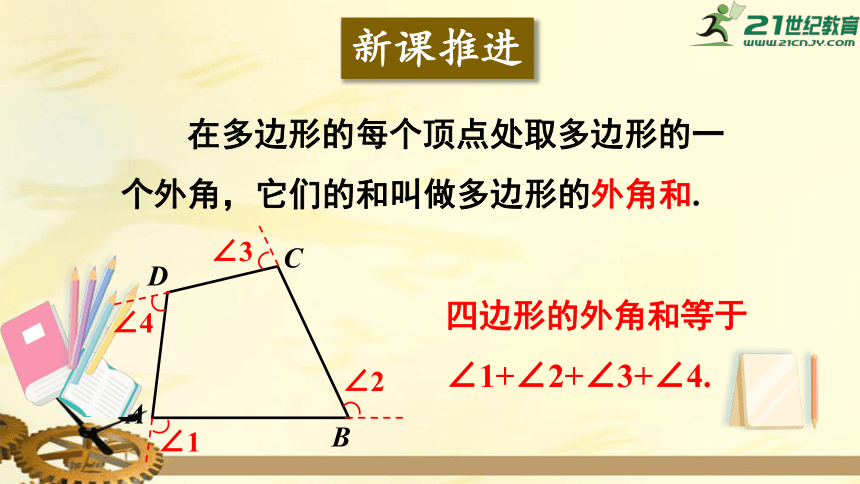
在多边形的每个顶点处取多边形的一个外角,它们的和叫做多边形的外角和.
A
B
C
D
∠1
∠2
∠3
∠4
四边形的外角和等于
∠1+∠2+∠3+∠4.
A
B
C
D
∠1
∠2
∠3
∠4
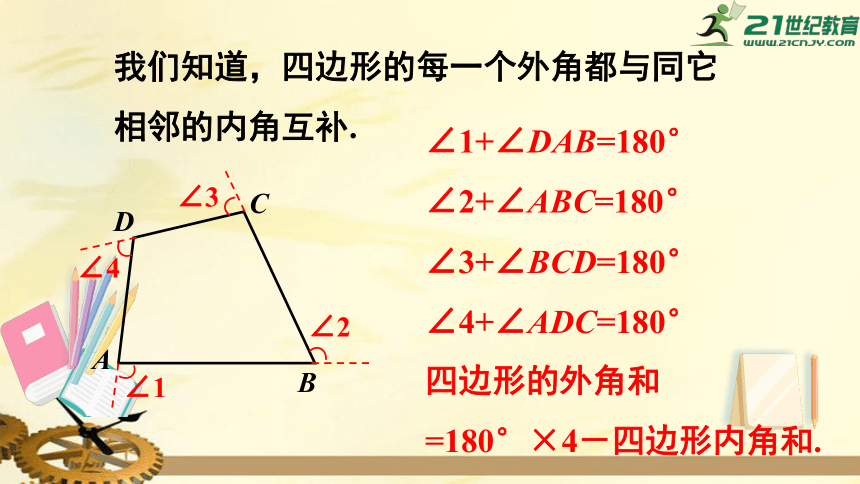
我们知道,四边形的每一个外角都与同它相邻的内角互补.
∠1+∠DAB=180°
∠2+∠ABC=180°
∠3+∠BCD=180°
∠4+∠ADC=180°
四边形的外角和
=180°×4-四边形内角和.
n
边形的外角和
=
180°n-180°(n-2)
=
360°
定理
n
边形的外角和等于
360°(n
为不小于
3
的整数).
如果一个多边形的每个外角都为40°,求这个多边形的边数.
练习
【分析】多边形的边数为n,则这个多边形有n个外角.
解
设多边形的边数为n,得40n=360°
n=9
正多边形
正三角形
正方形
正五边形
正六边形
多边形中,如果各条边都_____,各个角都_____,这样的多边形叫做正多边形.
相等
相等
例
求正六边形每个内角的度数.
解
正六边形的内角和为
(6-2)×180°=
720°
所以每个内角的度数为
720°÷6
=
120°.
四边形的不稳定性
三角形的三边一旦确定,其形状和大小就确定了,所以三角形具有_______.
稳定性
四边形各条边的长确定后,其形状不能确定,因此四边形具有__________.
a
a
不稳定性
在日常生活中,四边形的不稳定性,也有较为广泛的应用.
随堂练习
1.一个多边形的边都相等,它的内角一定都相等吗?
不一定,如菱形的边都相等,但内角不一定相等.
2.一个多边形的内角都相等,它的边一定都相等吗?
不一定,如矩形的内角都相等,但边未必都相等.
3.若一个多边形的内角和比它的外角和的
3
倍多
180°,则它是几边形?
解
由于外角和为
360°.
(n-2)×180°=
360°×3
+
180°
n
=
9.
答:它是
9
边形.
4.下图是一个活动挂衣架,你能说明制作这个活动挂衣架的依据吗?你知道如何使用这个挂衣架吗?
解:制作的依据是四边形具有不稳定性.不用时,把衣架两端往中间挤,以便收起,使用时,可以把衣架朝两边拉开.
5.正多边形的每个内角可能是:(1)75°;(2)90°;(3)120°吗?说明理由.
分析
正
n
边形的每个角为
.
(n-2)·180°
n
(n-2)·180°
n
解:(1)
=
75°
n≈3.43
.
n
不是整数,所以这个正多边形不存在.
课后作业
1.从教材习题中选取.
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第
2
课时
正多边形及四边形的不稳定性
沪科版·八年级数学下册
上课课件
第19章
四边形
学习目标
【知识与技能】
1.认识多边形,理解多边形的相关概念
2.掌握多边形的内角和与外角和公式,进一步了解转化的数学思想
3.会用多边形的内角和公式求多边形的内角和并会逆用公式求多边形的边数.
【过程与方法】
1.让学生经历猜想、探索、推理、归纳等过程,发展学生的合情推理能力和语言表达能力,掌握复杂问题化为简单问题,化未知为已知的思想方法.
2.通过把多边形转化为三角形,体会转化思想在几何中的运用,让学生体会从特殊到一般的认识问题的方法.
3.通过探索多边形的内角和与外角和,让学生尝试从不同的角度寻求解决问题的方法,并能有效地解决问题.
【情感与态度】
通过学生间交流、探索,进一步激发学生的学习热情,求知欲望,养成良好的数学思维品质.
【教学重点】
探索多边形的内角和及外角和公式
【教学难点】
如何把多边形转化成三角形,用分割多边形法推导多边形的内角和与外角和.
新课导入
多边形内角和定理:n
边形的内角和等于_________(n
为不小于
3
的整数)
(n-2)·180°
新课推进
在多边形的每个顶点处取多边形的一个外角,它们的和叫做多边形的外角和.
A
B
C
D
∠1
∠2
∠3
∠4
四边形的外角和等于
∠1+∠2+∠3+∠4.
A
B
C
D
∠1
∠2
∠3
∠4
我们知道,四边形的每一个外角都与同它相邻的内角互补.
∠1+∠DAB=180°
∠2+∠ABC=180°
∠3+∠BCD=180°
∠4+∠ADC=180°
四边形的外角和
=180°×4-四边形内角和.
n
边形的外角和
=
180°n-180°(n-2)
=
360°
定理
n
边形的外角和等于
360°(n
为不小于
3
的整数).
如果一个多边形的每个外角都为40°,求这个多边形的边数.
练习
【分析】多边形的边数为n,则这个多边形有n个外角.
解
设多边形的边数为n,得40n=360°
n=9
正多边形
正三角形
正方形
正五边形
正六边形
多边形中,如果各条边都_____,各个角都_____,这样的多边形叫做正多边形.
相等
相等
例
求正六边形每个内角的度数.
解
正六边形的内角和为
(6-2)×180°=
720°
所以每个内角的度数为
720°÷6
=
120°.
四边形的不稳定性
三角形的三边一旦确定,其形状和大小就确定了,所以三角形具有_______.
稳定性
四边形各条边的长确定后,其形状不能确定,因此四边形具有__________.
a
a
不稳定性
在日常生活中,四边形的不稳定性,也有较为广泛的应用.
随堂练习
1.一个多边形的边都相等,它的内角一定都相等吗?
不一定,如菱形的边都相等,但内角不一定相等.
2.一个多边形的内角都相等,它的边一定都相等吗?
不一定,如矩形的内角都相等,但边未必都相等.
3.若一个多边形的内角和比它的外角和的
3
倍多
180°,则它是几边形?
解
由于外角和为
360°.
(n-2)×180°=
360°×3
+
180°
n
=
9.
答:它是
9
边形.
4.下图是一个活动挂衣架,你能说明制作这个活动挂衣架的依据吗?你知道如何使用这个挂衣架吗?
解:制作的依据是四边形具有不稳定性.不用时,把衣架两端往中间挤,以便收起,使用时,可以把衣架朝两边拉开.
5.正多边形的每个内角可能是:(1)75°;(2)90°;(3)120°吗?说明理由.
分析
正
n
边形的每个角为
.
(n-2)·180°
n
(n-2)·180°
n
解:(1)
=
75°
n≈3.43
.
n
不是整数,所以这个正多边形不存在.
课后作业
1.从教材习题中选取.
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
