19.2 平行四边形(第1课时) 平行四边形边、角的性质 课件(共32张PPT)
文档属性
| 名称 | 19.2 平行四边形(第1课时) 平行四边形边、角的性质 课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 17:39:23 | ||
图片预览







文档简介
(共32张PPT)
19.2
平行四边形
第
1
课时
平行四边形边、角的性质
沪科版·八年级数学下册
上课课件
学习目标
【知识与技能】
1.理解并掌握平行四边形的定义
2.掌握平行四边形的性质定理1及性质定理2
3.理解两条平行线的距离的概念4.培养学生综合运用知识的能力
【过程与方法】
经历探索平行四边形的有关概念和性质的过程,发展学生的探究意识和合情推理的能力.
【情感态度】
培养学生严谨的思维和勇于探索的思想意识,体会几何知识的内涵与实际应用价值.
【教学重点】
平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.
【教学难点】
运用平行四边形的性质进行有关的论证和计算.
新课导入
请找出图中的平行四边形,说明寻找的依据是什么?
定
义
两组对边_________的四边形叫做平行四边形.
分别平行
A
B
C
D
平行四边形用“
”表示,如图,平行四边形ABCD
记作“
”.
ABCD
平行四边形的边角关系
A
B
C
D
由平行四边形的定义,我们知道平行四边形的两组对边分别平行.
想
想
一
平行四边形还有什么性质?
猜想:平行四边形对角相等,对边相等.
怎样证明?
有关四边形的问题常常转化为三角形问题解决;平行四边形的一条对角线把平行四边形分成两个全等的三角形;为此,我们通过添加辅助线,构造两个三角形,通过三角形全等进行证明.
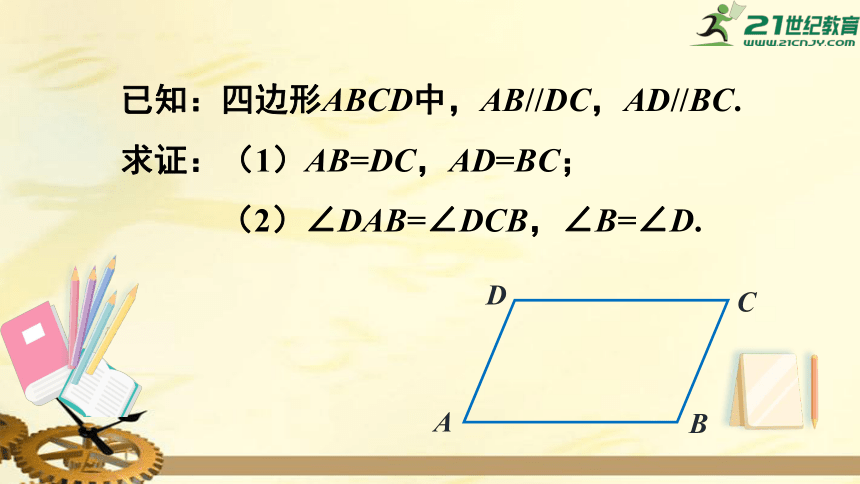
已知:四边形ABCD中,AB//DC,AD//BC.
求证:(1)AB=DC,AD=BC;
(2)∠DAB=∠DCB,∠B=∠D.
A
B
C
D
A
B
C
D
证明:
如图,连接AC.
(1)
∵AB∥DC,AD∥BC,
∴∠BAC
=∠DCA,∠BCA
=∠DAC.
在△ABC和△CDA中,
∠BAC
=∠DCA,
AC
=
CA,
∠BCA=∠DAC.
∴△ABC≌△CDA.(ASA)
(2)
∵由(1)知
△ABC
≌△CDA.
∴
AB
=
DC,AD
=
BC,∠B
=∠D.
A
B
C
D
∠DAB
=∠BAC
+∠DAC
=
∠DCA+∠BCA
=
∠DCB.
归纳小结
性质1
平行四边形的两组对边分别相等.
性质2
平行四边形的两组对角分别相等.
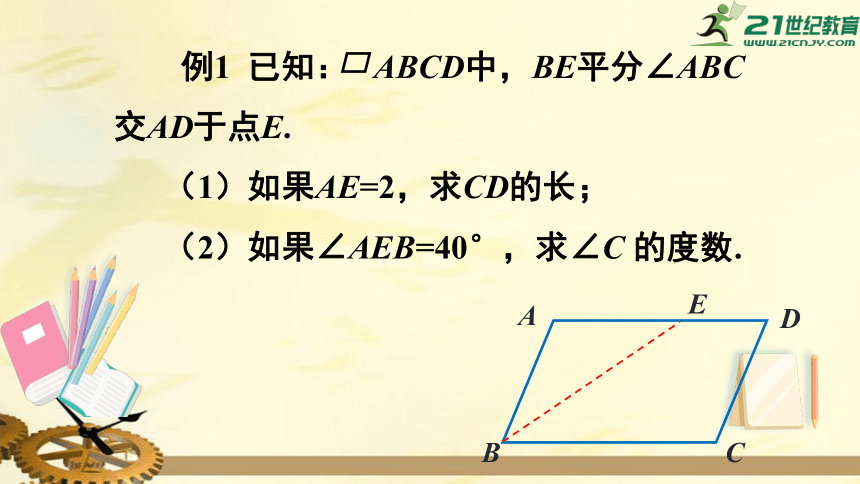
例1
已知:
ABCD中,BE平分∠ABC交AD于点E.
(1)如果AE=2,求CD的长;
(2)如果∠AEB=40°,求∠C
的度数.
A
B
C
D
E
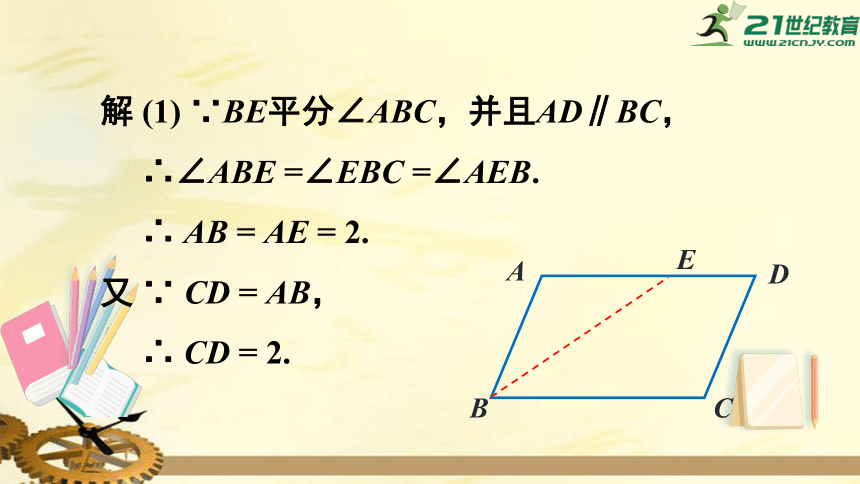
解
(1)
∵BE平分∠ABC,并且AD∥BC,
∴∠ABE
=∠EBC
=∠AEB.
∴
AB
=
AE
=
2.
又
∵
CD
=
AB,
∴
CD
=
2.
A
B
C
D
E
(2)
由
(1)知
∠ABE
=∠AEB
=
40°,
∴
∠A
=
180°-(40°+
40°)=100°.
又
∵
∠C
=
∠A,
∴
∠C
=
100°.
A
B
C
D
E
两条平行线之间的距离
直线l1//直线l2,AB,CD是夹在直线l1,l2之间的两条平行线段.
l1
l2
A
B
C
D
想一想:AB
是否等于CD?为什么?
由性质1
平行四边形对边相等.可得如下结论:
夹在两条平行线之间的_________相等.
平行线段
l1
l2
A
B
C
D
由上面的结论可以知道,如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等.
定义:两条平行线中,一条直线上任意一点到另一条直线的______叫做这两条平行线之间的距离.
距离
例2
已知:如图□ABCD
中,AB=4,AD=5,∠B=45°.
求直线
AD
和直线
BC
之间的距离,直线
AB
和直线
DC
之间的距离.
A
B
C
D
4
5
45°
解:过点
A
作AE⊥BC,AF⊥CD,垂足分别为点
E、点
F.
∴
线段
AE,AF
的长分别为点
A到直线
BC
和直线
CD
的距离.
A
B
C
D
4
5
45°
E
F
∴
线段AE的长为直线
AD和直线
BC
之间的距离.
线段
AF
的长为直线
AB
和直线
CD
之间的距离.
∵在
Rt△ABE
中,∠AEB=90°,
∠B=45°,AB=4
∴∠B=∠BAE,
∴BE=AE.
又∵AE2+BE2=AB2
∴2AE2=16.
∴AE=
.
A
B
C
D
4
5
45°
E
F
同理:AF=
.
所以直线
AD
和直线
BC
之间的距离为
,
直线
AB
和直线
CD
之间的距离为
.
A
B
C
D
4
5
45°
E
F
例3
已知:如图,过
△ABC
的三个项点,分别作对边的平行线,这三条直线两两相交,得
△A′B′C′
.
求证:△ABC
的顶点分别是△A′B′C′
三边的中点.
分析如图,要证明点
A
是
B′C′
的中点,只要证明AB′
=
AC′.
证明:∵AB∥B′C,BC∥AB′
,
∴AB′
=
BC.
同理:AC′
=
BC,
∴AB′
=
AC′.
同理:BC′
=
BA′,CA′
=
CB′.
所以
△ABC
的顶点分别是△A′B′C′
三边的中点.
随堂练习
1.在
中,∠A∶∠B
=
2∶3,求各角的度数.
ABCD
解:∵四边形ABCD为平行四边形,
∴∠A+∠B=180°,∠A=∠C,∠B=∠D.
又∵∠A∶∠B=2∶3,
∴∠A=∠C=72°,∠B=∠D=108°.
2.已知
的周长为
28
cm,AB∶BC
=
3∶4,求它的各边的长.
ABCD
A
B
C
D
解:∵四边形
ABCD
为平行四边形,
∴AB
=
CD,AD
=
BC.
又∵C
ABCD
=
AB+BC+CD+AD
=
28cm,
且
AB∶BC
=
3∶4,
∴AB
=
CD
=
6cm,AD
=
BC
=
8cm.
A
B
C
D
3.
如图,在
中,已知
AD
=
8
cm,AB
=
6
cm,DE
平分∠ADC
交
BC
边于点
E,则BE的长为________.
2
cm
ABCD
A
B
C
D
E
4.
平行四边形的一条角平分线分对边为
3
和4
两部分,求平行四边形的周长.
A
B
D
C
E
1
2
3
解
如图,∵
ABCD中,
AD∥BC,∴∠1=∠3,
又∠1=∠2,∴∠2=∠3,∴AB=BE.
当BE=3时,AB=BE=3,∴
ABCD的周长为:
(AB+BC)×2=(3+7)×2=20.
A
B
D
C
E
1
2
3
当BE=4时,AB=BE=4,
∴
ABCD的周长为:
(AB+BC)×2=(4+7)×2=22.
A
B
D
C
E
1
2
3
课后作业
1.从教材习题中选取.
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
19.2
平行四边形
第
1
课时
平行四边形边、角的性质
沪科版·八年级数学下册
上课课件
学习目标
【知识与技能】
1.理解并掌握平行四边形的定义
2.掌握平行四边形的性质定理1及性质定理2
3.理解两条平行线的距离的概念4.培养学生综合运用知识的能力
【过程与方法】
经历探索平行四边形的有关概念和性质的过程,发展学生的探究意识和合情推理的能力.
【情感态度】
培养学生严谨的思维和勇于探索的思想意识,体会几何知识的内涵与实际应用价值.
【教学重点】
平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.
【教学难点】
运用平行四边形的性质进行有关的论证和计算.
新课导入
请找出图中的平行四边形,说明寻找的依据是什么?
定
义
两组对边_________的四边形叫做平行四边形.
分别平行
A
B
C
D
平行四边形用“
”表示,如图,平行四边形ABCD
记作“
”.
ABCD
平行四边形的边角关系
A
B
C
D
由平行四边形的定义,我们知道平行四边形的两组对边分别平行.
想
想
一
平行四边形还有什么性质?
猜想:平行四边形对角相等,对边相等.
怎样证明?
有关四边形的问题常常转化为三角形问题解决;平行四边形的一条对角线把平行四边形分成两个全等的三角形;为此,我们通过添加辅助线,构造两个三角形,通过三角形全等进行证明.
已知:四边形ABCD中,AB//DC,AD//BC.
求证:(1)AB=DC,AD=BC;
(2)∠DAB=∠DCB,∠B=∠D.
A
B
C
D
A
B
C
D
证明:
如图,连接AC.
(1)
∵AB∥DC,AD∥BC,
∴∠BAC
=∠DCA,∠BCA
=∠DAC.
在△ABC和△CDA中,
∠BAC
=∠DCA,
AC
=
CA,
∠BCA=∠DAC.
∴△ABC≌△CDA.(ASA)
(2)
∵由(1)知
△ABC
≌△CDA.
∴
AB
=
DC,AD
=
BC,∠B
=∠D.
A
B
C
D
∠DAB
=∠BAC
+∠DAC
=
∠DCA+∠BCA
=
∠DCB.
归纳小结
性质1
平行四边形的两组对边分别相等.
性质2
平行四边形的两组对角分别相等.
例1
已知:
ABCD中,BE平分∠ABC交AD于点E.
(1)如果AE=2,求CD的长;
(2)如果∠AEB=40°,求∠C
的度数.
A
B
C
D
E
解
(1)
∵BE平分∠ABC,并且AD∥BC,
∴∠ABE
=∠EBC
=∠AEB.
∴
AB
=
AE
=
2.
又
∵
CD
=
AB,
∴
CD
=
2.
A
B
C
D
E
(2)
由
(1)知
∠ABE
=∠AEB
=
40°,
∴
∠A
=
180°-(40°+
40°)=100°.
又
∵
∠C
=
∠A,
∴
∠C
=
100°.
A
B
C
D
E
两条平行线之间的距离
直线l1//直线l2,AB,CD是夹在直线l1,l2之间的两条平行线段.
l1
l2
A
B
C
D
想一想:AB
是否等于CD?为什么?
由性质1
平行四边形对边相等.可得如下结论:
夹在两条平行线之间的_________相等.
平行线段
l1
l2
A
B
C
D
由上面的结论可以知道,如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等.
定义:两条平行线中,一条直线上任意一点到另一条直线的______叫做这两条平行线之间的距离.
距离
例2
已知:如图□ABCD
中,AB=4,AD=5,∠B=45°.
求直线
AD
和直线
BC
之间的距离,直线
AB
和直线
DC
之间的距离.
A
B
C
D
4
5
45°
解:过点
A
作AE⊥BC,AF⊥CD,垂足分别为点
E、点
F.
∴
线段
AE,AF
的长分别为点
A到直线
BC
和直线
CD
的距离.
A
B
C
D
4
5
45°
E
F
∴
线段AE的长为直线
AD和直线
BC
之间的距离.
线段
AF
的长为直线
AB
和直线
CD
之间的距离.
∵在
Rt△ABE
中,∠AEB=90°,
∠B=45°,AB=4
∴∠B=∠BAE,
∴BE=AE.
又∵AE2+BE2=AB2
∴2AE2=16.
∴AE=
.
A
B
C
D
4
5
45°
E
F
同理:AF=
.
所以直线
AD
和直线
BC
之间的距离为
,
直线
AB
和直线
CD
之间的距离为
.
A
B
C
D
4
5
45°
E
F
例3
已知:如图,过
△ABC
的三个项点,分别作对边的平行线,这三条直线两两相交,得
△A′B′C′
.
求证:△ABC
的顶点分别是△A′B′C′
三边的中点.
分析如图,要证明点
A
是
B′C′
的中点,只要证明AB′
=
AC′.
证明:∵AB∥B′C,BC∥AB′
,
∴AB′
=
BC.
同理:AC′
=
BC,
∴AB′
=
AC′.
同理:BC′
=
BA′,CA′
=
CB′.
所以
△ABC
的顶点分别是△A′B′C′
三边的中点.
随堂练习
1.在
中,∠A∶∠B
=
2∶3,求各角的度数.
ABCD
解:∵四边形ABCD为平行四边形,
∴∠A+∠B=180°,∠A=∠C,∠B=∠D.
又∵∠A∶∠B=2∶3,
∴∠A=∠C=72°,∠B=∠D=108°.
2.已知
的周长为
28
cm,AB∶BC
=
3∶4,求它的各边的长.
ABCD
A
B
C
D
解:∵四边形
ABCD
为平行四边形,
∴AB
=
CD,AD
=
BC.
又∵C
ABCD
=
AB+BC+CD+AD
=
28cm,
且
AB∶BC
=
3∶4,
∴AB
=
CD
=
6cm,AD
=
BC
=
8cm.
A
B
C
D
3.
如图,在
中,已知
AD
=
8
cm,AB
=
6
cm,DE
平分∠ADC
交
BC
边于点
E,则BE的长为________.
2
cm
ABCD
A
B
C
D
E
4.
平行四边形的一条角平分线分对边为
3
和4
两部分,求平行四边形的周长.
A
B
D
C
E
1
2
3
解
如图,∵
ABCD中,
AD∥BC,∴∠1=∠3,
又∠1=∠2,∴∠2=∠3,∴AB=BE.
当BE=3时,AB=BE=3,∴
ABCD的周长为:
(AB+BC)×2=(3+7)×2=20.
A
B
D
C
E
1
2
3
当BE=4时,AB=BE=4,
∴
ABCD的周长为:
(AB+BC)×2=(4+7)×2=22.
A
B
D
C
E
1
2
3
课后作业
1.从教材习题中选取.
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
